带有智能领导者的网络系统分群投影一致性

陈良康，过榴晓，杨永清

江南大学 理学院，江苏 无锡214122

1 引言

进入21 世纪以来，随着人工智能技术的快速发展和在社会实际中的广泛应用，对多智能体系统的研究吸引了国内外众多学者的关注。一致性问题作为多智能体系统控制的最基本问题之一，它指的是所有的智能体通过信息交流使得各自的状态趋于一致或者相同。文献[1]从统计力学的角度分析了粒子群的一致性问题，为后期一致性问题的研究工作提供了基础。文献[2]提出了一阶多智能系统一致性的基本理论框架。而关于二阶多智能系统一致性的研究热潮始于2007 年，至今已经取得了丰富的成果[3-6]。

上述研究的目标都是使系统内所有智能体的位置、速度等状态分别收敛到同一个值，即网络系统中的一致性平衡点。但随着人们对应用系统的要求不断增大，使得系统规模的增加以及复杂度的提高，导致单一平衡点无法满足系统的控制需求，因而越来越多的人开始关注分群（分组）一致性。网络中的所有智能体被分为若干群，相同群中的所有智能体都收敛至一个状态，不同群中的收敛状态不同。文献[7-8]等研究了在无向强联通网络拓扑图下一阶多智能体系统分群收敛的若干判据，并将该结论在切换拓扑以及时滞情形下进行了推广；文献[9]通过有限时间分析研究了分群一致。文献[10-12]进一步研究了二阶系统实现分群一致的充分条件。文献[13]利用一种新的图解方法，建立了有向拓扑下具有时变参考信号的二阶系统分群一致准则。近年来，针对群一致的研究，人们又提出了一种特殊的分群一致性——二分一致，例如文献[14]研究了系统当符号图在结构上达到平衡时的二分一致性，文献[15-16]分别讨论了在有领导者和无领导者的情况下线性多智能体系统实现合作与对抗的网络节点二分一致的条件。然而在以上对分群一致的研究中，不同群内收敛状态的关系是固定不变的，只能呈现相同或者相反的关系，这给控制系统一定程度的限制性。另外，在现实中，某些执行器可能发生故障，导致系统无法实现预期目标。但是绝大多数文献针对解决执行器故障问题仅局限于未分群情况，如文献[17]基于事件触发机制下设计了一个控制算法，确保在执行器发生故障时系统的有界性。

针对以上问题，受文献[14-15，17]的启发，本文研究领导-跟随多智能体系统分群投影一致性，同时考虑执行器发生故障时系统的有界性问题。本文工作有如下创新：首先和已有大部分文献相比本文研究的分群投影一致是一种更为普遍的一致性，包含完全一致，分组与反分组一致作为其特殊情况，并且不需要符号图在结构上达到平衡；其次针对分群结构下执行器故障问题，引入了一个智能领导者，在新的控制算法能够保证跟踪误差有界，与传统模型相比大大提高了系统的容错性；最后通过改变控制参数可以任意改变不同群内收敛状态的关系，给控制系统以更大的自由度。

2 预备知识及问题描述

2.1 代数图论

2.2 模型描述

T 、Tˉ表示时间间隔的联合，当t ∈T 时，智能领导者采用控制输入式（4a），这意味着智能领导者只受外部输入的影响，当t ∈Tˉ时，智能领导者采用控制输入式（4b），即智能领导者受来自其邻居跟随者的反馈影响。显然

假设1网络拓扑图G 是联通的，跟随者之间的连接是无向的，领导者和跟随者之间的连接是有向的。

假设2领导者至少是一个跟随者的邻居，此即意味着跟随者能直接或间接的受领导者影响。

引理1[18]由Lyapunov 稳定性定理，如果对于每一个子系统，能构造一个公共的Lyapunov函数，那么切换系统可以任意切换，并且切换系统的稳定性能够实现。

3 主要结果

3.1 系统未发生执行器故障

3.2 系统发生执行器故障

4 数值仿真

考虑由8 个节点组成的多智能体系统，其中包括1个领导者和7 个跟随者。编号为1～4 的智能体分为1群，编号为5～7 的智能体分为2 群。系统的固定拓扑图G如图1所示。

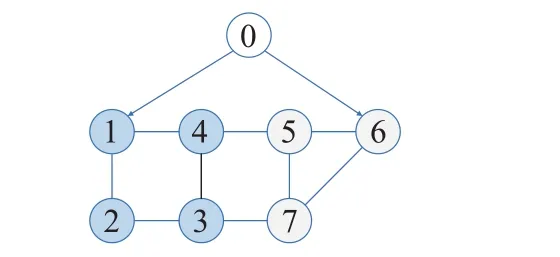
图1 固定拓扑图G

经计算可得：λmin(L+H)=0.4，若α取2，β取1，则满足定理1 中条件，当投影参数c取1 和-1 时，系统轨迹图分别如图2和3所示，此时多智能体系统（1）在控制协议（2）～（3）作用下能够实现在分群投影一致性。通过选取不同的投影参数进行比较发现，系统的收敛性不受投影参数的影响，如图2和图3所示，系统的位置状态和速度状态均分别在20 s和15 s以后达到一致。

假设编号为4 和5 的智能体在第25 s 时发生执行器故障，投影参数c取-1。当系统无智能领导者控制时，即系统发生执行器故障前后，领导的控制算法并未发生改变，由图4知系统的跟踪误差

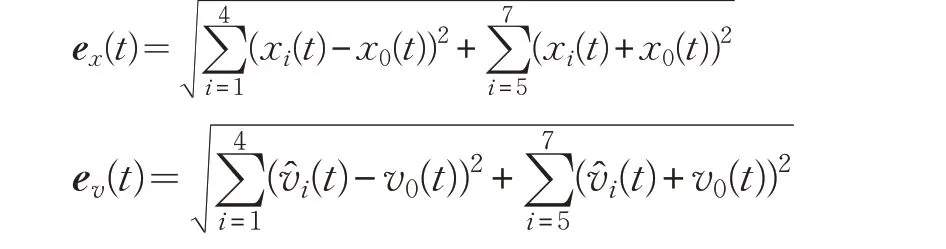
会逐渐变大，此时无法实现分群投影一致性。由定理2 知：当系统有智能领导者控制时，随着误差变大，满足事件触发函数（7），此时智能领导者算法会由式（4a）切换到式（4b），在控制协议（2）和（3）作用下系统的误差演化图如图5所示。由图5知系统跟踪误差在系统发生执行错误时有界，且大约在30 s 时，系统能够递归自修复达到分群投影一致。

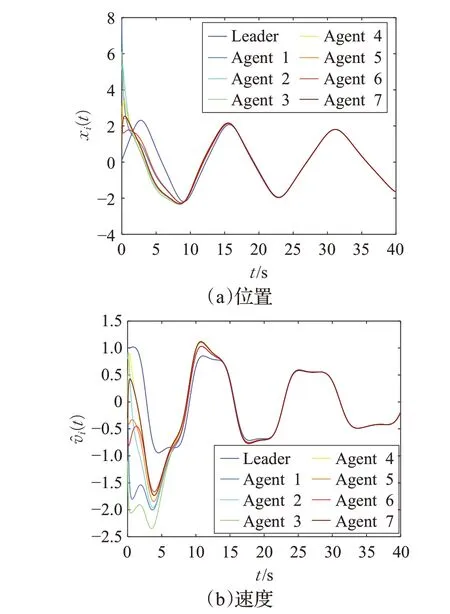
图2 投影参数c=1 时系统轨迹图

5 结束语

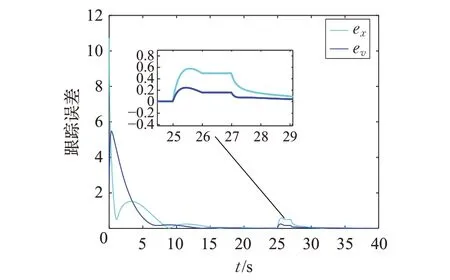
图5 误差系统演化图（有智能领导者控制）

针对多智能体系统在分群结构下投影一致性问题，本文引入了一个智能领导者，设计了一个新颖的分布式控制协议，利用矩阵理论和Lyapunov 稳定性理论给出了系统实现分群投影一致的充分条件。当系统内发生执行器故障时，基于拉普拉斯变换性质，分析了系统跟踪误差的有界性。数值仿真验证了结果的正确性。然而自然界中的个体和工程系统无论在结构还是功能上都存在差异，智能体的动力学行为也可能不同，因此在今后的工作中，将研究由一阶和二阶智能体组成的混合阶（异构）多智能体系统在分群结构下投影一致性问题。