PCBA柔性作业车间等量分批调度问题研究

黄夏宝，杨立熙，傅光炎

（1.福建江夏学院 工商管理学院，福州 350108；2.福州大学 经济与管理学院，福州 350108）

0 引言

近年来，电子产品不断朝着多元化、定制化方向演进，印刷电路板组装（Print Circuit Board Assembly，PCBA）的多品种、变批量生产模式成为主流，因此在快速性和灵活性方面对电子制造企业提出了更高的要求，PCBA车间的生产调度优化成为亟需解决的问题[1,2]。

PCBA车间调度问题主要集中在表面贴装技术（Surface Mounted Technology，SMT）子车间的调度研究，包括SMT车间中多品种PCB贴装生产排程优化[3]、生产线的负荷均衡化问题[4]、产线分配和组间排序问题[5]、多条生产线的调度问题[6,7]。PCBA车间生产调度问题是一个集批量规划和生产排程的综合性问题[8]。在多品种、小批量的PCBA分批调度问题中，有通过反应式禁忌搜索算法确定PCB组内和组间的序列[9]；随机的方式生成子批大小与个数[10]；订单批次与批量可变的柔性分批调度方法[11,12]；分批具有方向性的试探法[13]；将订单中每个工件都作为一个批次的订单批量的大小与排序动态结合的方法[14]。

PCBA车间的主板加工主要包含SMT、自动插件（Automatic Insertion，AI）、手工插件（Manual Insertion，MI）三道流程，现阶段大部分文献集中于SMT子车间生产调度的研究，而对PCBA全局的研究较少。在实际排程过程中，三个子车间的排程相互独立，排程人员仅负责各自车间的排程任务，且采用手工Excel排程的方法，缺乏协调性与高效性；排程人员仅对超大订单进行分批，未考虑其它批量生产类型的分批。因此，设计自动排程的程序对PCBA车间全局生产在多种批量生产类型下分批调度的研究很有必要。文献中不少分批策略需要不断尝试不同批量划分的解，搜索效率低，多用于解决较小批量的生产调度，而本文为解决PCBA车间存在的不少中、大批量的问题，采用等量分批调度策略。

本文面向PCBA车间生产全流程，构建了柔性作业车间等量分批调度模型。针对遗传算法（Genetic Algorithm，GA）存在的过早收敛、容易陷入局部最优的缺点，设计了改进的遗传模拟退火算法（Genetic Simulated Annealing Algorithms，GASA）来求解该问题。

1 PCBA柔性作业车间分批调度模型

1.1 问题描述

PCBA车间中每道流程都有多条可选择的生产线，且加工效率各不相同。排程任务有多个订单，受产能约束的影响，完工时间越短越好。在加工的过程需要考虑加工顺序与设备资源等约束，本文假设：1）同一时刻，每条生产线上最多有一个订单批次被加工；2）同一时刻，每个订单批次的同道工序只允许在同一条生产线上加工；3）每个订单的批次加工过程不允许间断；4）订单在生产线间的运输时间记为零；5）每个订单批次都可在t=0时被加工。

1.2 模型的建立

PCBA柔性作业车间分批调度模型可描述为：PCBA车间有I个订单，每个订单有Qi个相同的产品、hi道工序，分批数为N。每个子批在k条可选择的生产线上加工，同一工序在不同生产线上的加工时间各不相同。Oijr为订单i第j批次的第r道工序；Mijr为工序Oijr的可选择生产线数；Pijrk为工序Oijr在生产线k上的加工时间；Sijr、Cijr分别为工序Oijr的开始、完成时间；T为切换时间。本文以最小化最大完工时间为模型的目标函数：

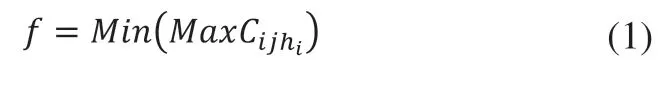
针对分批调度问题，约束如下：

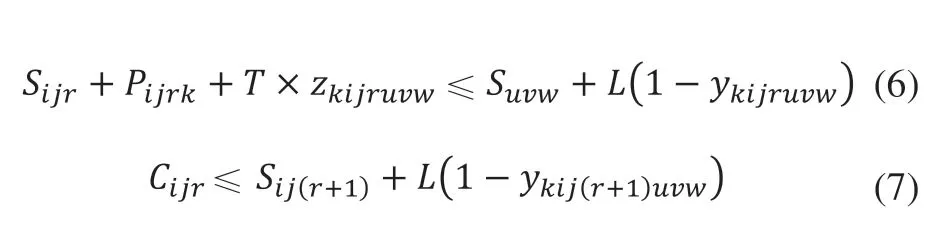
其中：订单序号i，u=1，2，…，I，批次序号j，v=1，2，…，N，r=1，2，…，hi，w=1，2，…，hh，k=1，2，…，M；

上述公式中，xkijr、ykijruvw、zkijruvw为决策变量，式(2)、式(3)表示同一订单批次的工序间加工顺序约束；式(4)表示加工为非抢占式；式(5)表示每个订单同一批次的完工时间约束；式(6)、式(7)表示同一时刻同一生产线只能加工一道工序。

2 分批调度混合算法

本文将整个求解过程分为订单批量分批、子批排程两个阶段，如图1所示。其中批量分批包括批量生产类型划分和等量分批两个子问题，子批排程又包括子批排序和生产线选择两个子问题。

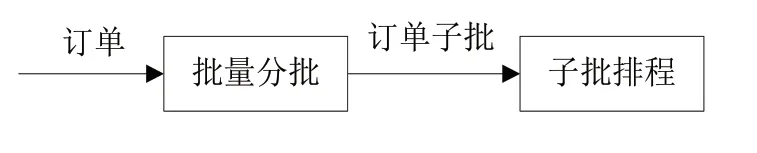
图1 订单分批排程流程图

2.1 批量分批

批量的划分标准并非以量作为唯一衡量标准，而是需要与产品的价值量、加工难度等因素综合考虑。依据技术经济原则，确立了一种批量划分的经验方法，该种划分方法与切换时间密切相关[15]。需要给定一个生产线的损失系数阈值，引用文献[15]中式(8)与表1阈值系数。

式中：δ为生产线损失系数阈值；tαd为某订单总切换时间；t某订单单个产品总的加工时间；Qmin批量数量界限。

PCBA加工的四道工序总切换时间tαd=7200s。根据PCBA车间各生产线加工时间，求得单件产品总加权时间t=145s，再依据中件的划分确定各生产类型的批量范围。

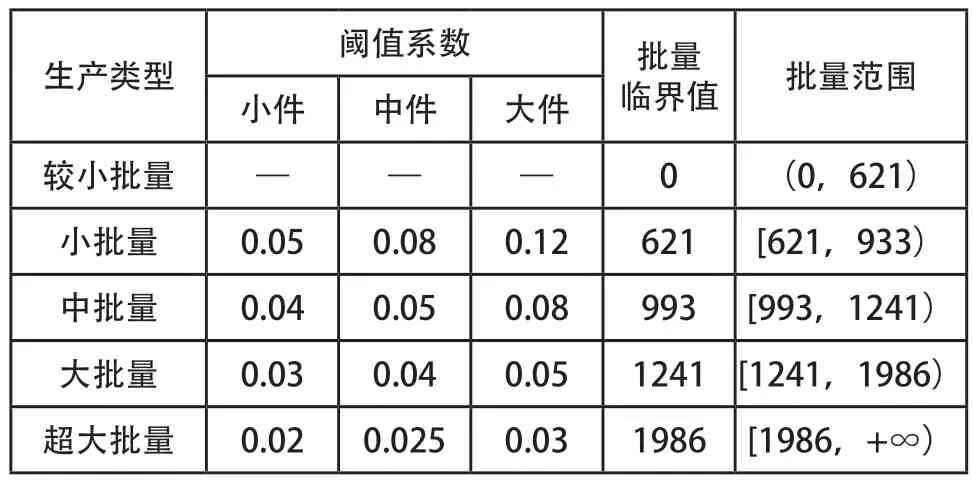
表1 阈值系数与生产类型批量范围表

通常，批量的大小与生产周期呈现“U”型的关系，批量过大或过小都会影响生产的效率。等量分批过程中可能遇到无法均匀分配的问题，此时需对算法进行优化，如某一大批量订单批量为1550，若分3批，（批量/分批数）后的值取整作为前2批批量，余下作为第3个子批批量，结果为[516，516，518]。

2.2 子批排程算法

2.2.1 GASA算法流程

本文采用GASA算法来解决子批排程问题，具体流程如图2所示。

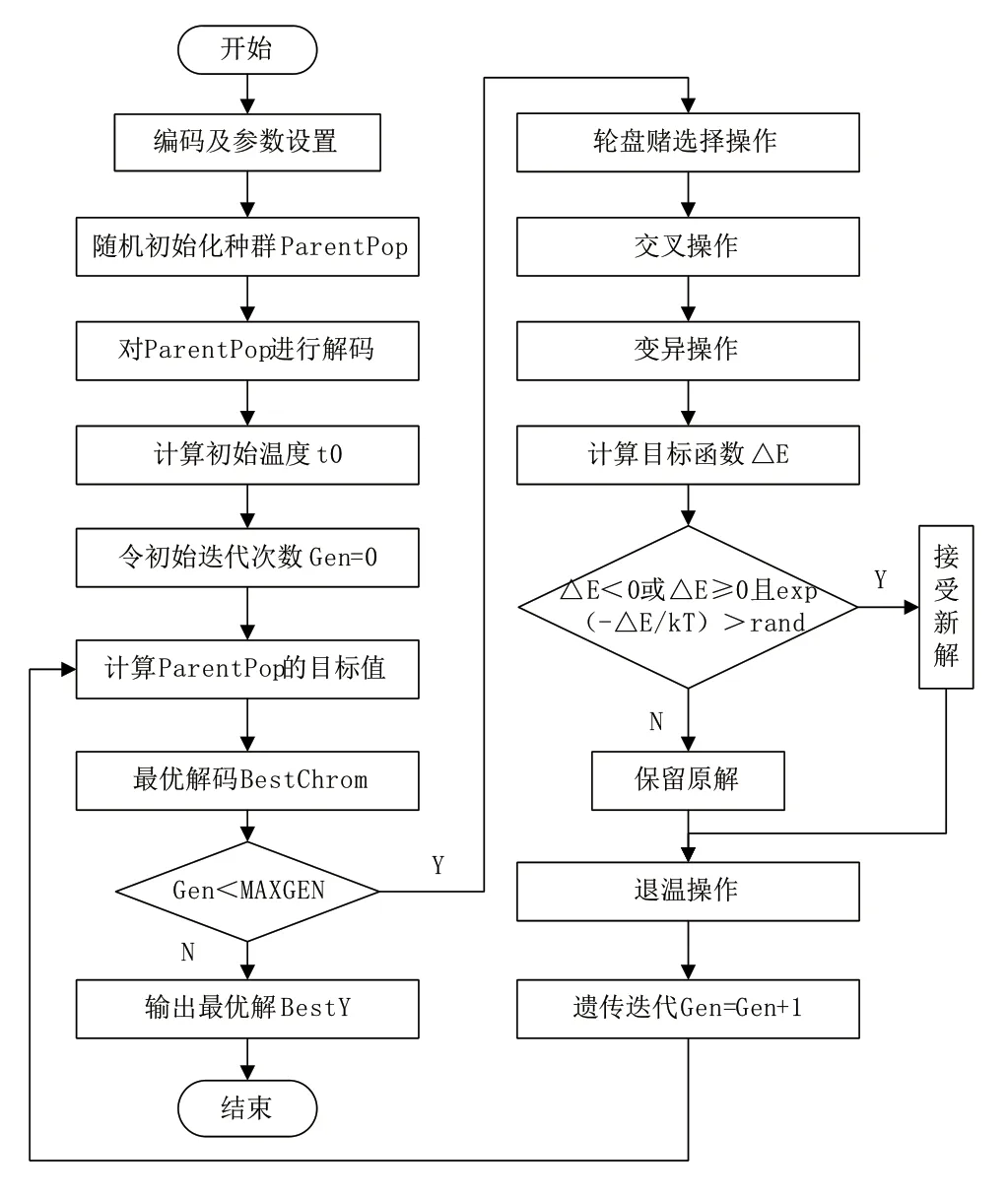
图2 遗传-模拟退火算法流程图

2.2.2 编码与解码

分段编码有易于操作和表达的特性，因此本文运用分段编码与OSMS的整数编码[16]相结合的方式，将编码分为工序排序和生产线选择两部分，如图3所示。

1）子批工序排序部分

基因位表示订单号&批次号组合。订单&批次号出现的次序表示该订单批次的工序间的加工先后次序，第h次出现的订单&批次号表示该订单批次的第h道工序，如工序O121表示订单1的第2批次的第1道工序。由于即使在订单批次工序数不确定、调度模式变化的情况下该种编码方式依然适用，表现出较高的柔性而被广泛使用。

2）生产线选择部分

前部分工序排序的染色体和后部分生产线选择的染色体是一一对应的。生产线编码上染色体的数字代表对应工序的可选择加工生产线的序号。这种生产线编码方式能够保证后续进行算法的各项操作依旧能获得可行解。

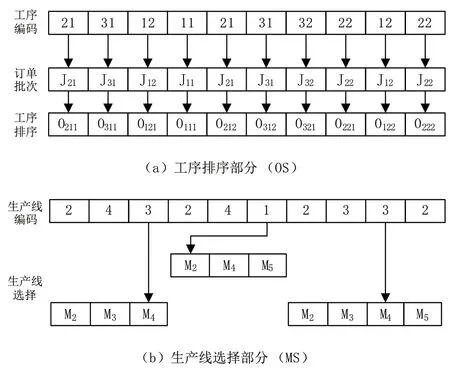
图3 分段编码

解码也需要分别对工序排序部分和生产线选择两个部分进行操作，算法如下：染色体上从左到右依次读取工序排序部分中的基因值，将每个值转化为对应的各道工序Oijr；相应的，可以算出Oijr在生产线Mk上的加工时间Pijrk；假设生产线Mk上两个相邻订单批次工序Ouvw、Oijr，若其订单号（u，i）、工序号（w，r）相同，批次不同，则不需要换批时间；否则需要添加换批时间T。

2.2.3 交叉与变异操作

本文采用洗牌交叉与单点交叉结合的方式对工序排序部分进行交叉。洗牌交叉：随机打乱种群中各个个体的排序，以避免每次迭代后，依旧选择相同次序的两个父代个体进行交叉操作；单点交叉：在基因串长度的范围内产生一个随机变异位置点Pos，交换两父代染色体的前1～Pos位基因，用父代染色体多余基因修补子代缺失基因，将两个个体基因串的后位的生产线选择部分也做相同的交叉操作，保持原有工序排序的各个基因对应的生产线选择不变。

变异操作主要针对生产线选择部分，通过随机选择变异位置，在需要变异的位置上以更高的概率选择加工时间最少的生产线，从而达到局部优化的目的。

2.2.4 模拟退火操作

本文将模拟退火算法的Metropolis准则与遗传算法串联使用，扩展到遗传算法的交叉、变异操作后的新个体接受准则中，先采用SWAP操作产生新个体，若新个体结果优于原有个体，则接受新个体；若新个体结果劣于原有个体，则以一定概率接受新个体。在这里引入了初始温度t0以及状态接受函数k，式(11)为退温函数。

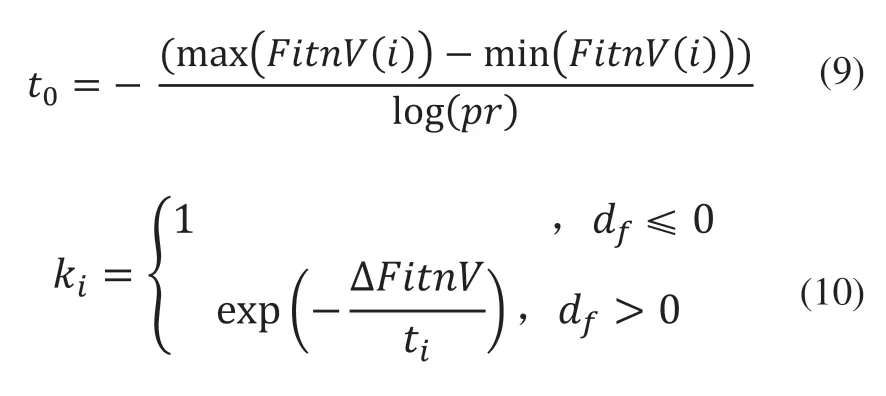
式中FitnV（i）为种群中个体i的适应度值，df为原个体与新个体的适应度值差值，pr为初始接受概率，λ为温度衰减系数，通过多次实验验证，本文pr取0.8，λ取0.95。

3 实例分析

某PCBA车间由SMT车间、AI车间和MI车间构成，共有生产线9条，其中SMT车间4条、AI车间3条、MI车间2条，每个子车间内的生产线都具有相同的功能，但由于生产线设备组成型号与新旧程度不一，加工效率也有所不同。某一周的预先排程如表2所示，共有10个订单需要在PCBA车间加工，加工流程为：SMT B面加工→SMT T面加工→AI加工→MI加工，子批之间的换批时间为30min。PCBA车间各生产线加工时间如表3所示。

实例分析有两个目的：一是比较本文提出的算法与遗传算法在求解实际调度问题方面的表现；二是研究不同生产类型下批量与分批数之间的关系。算法采用MATLAB编程实现。

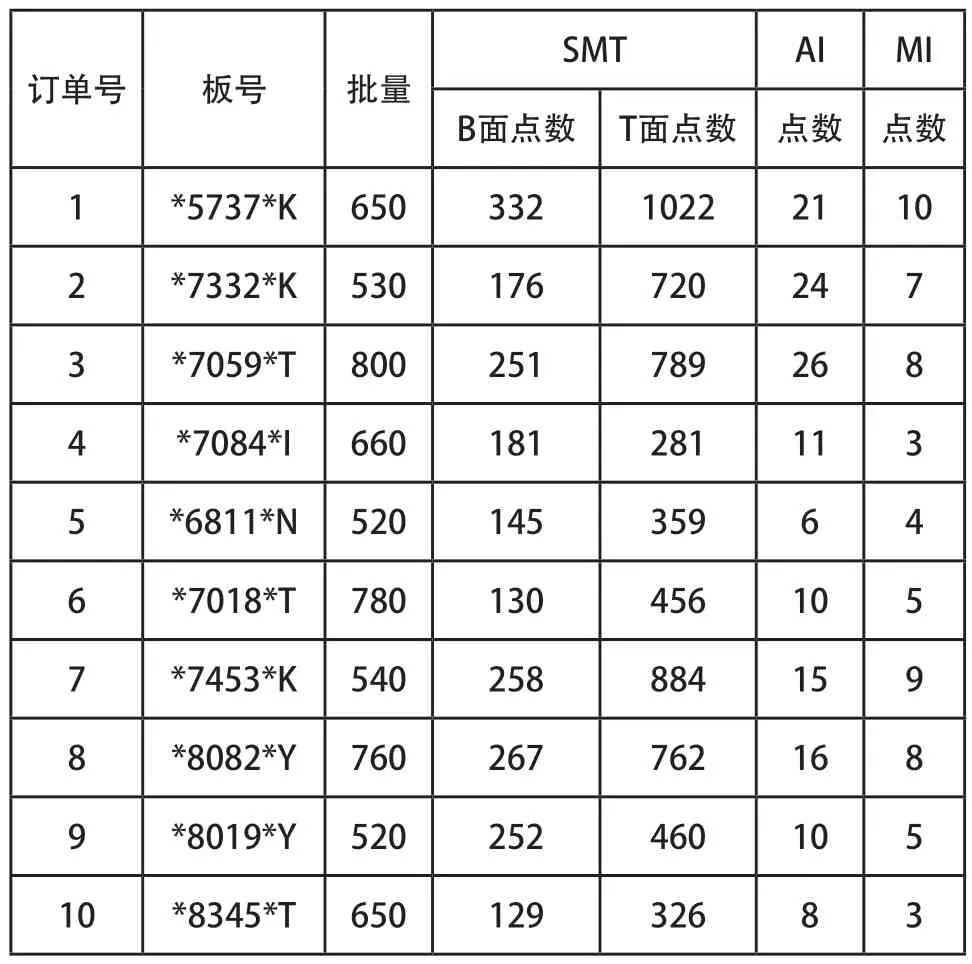
表2 各订单的批量及其加工点数

3.1 GA与GASA算法比较

算法参数的设置对求解影响很大，通过实验仿真验证得出种群大小、交叉概率、变异概率的最优取值分别为200、0.8、0.02。分别使用GA与GASA算法对不同分批数的订单各运行10次，结果如表5所示。f值为目标函数的解，即为最大完工时间值；Min（f）、Avg（f）分别表示运行10次的结果中的最优值、平均值；t为算法的运行时间。

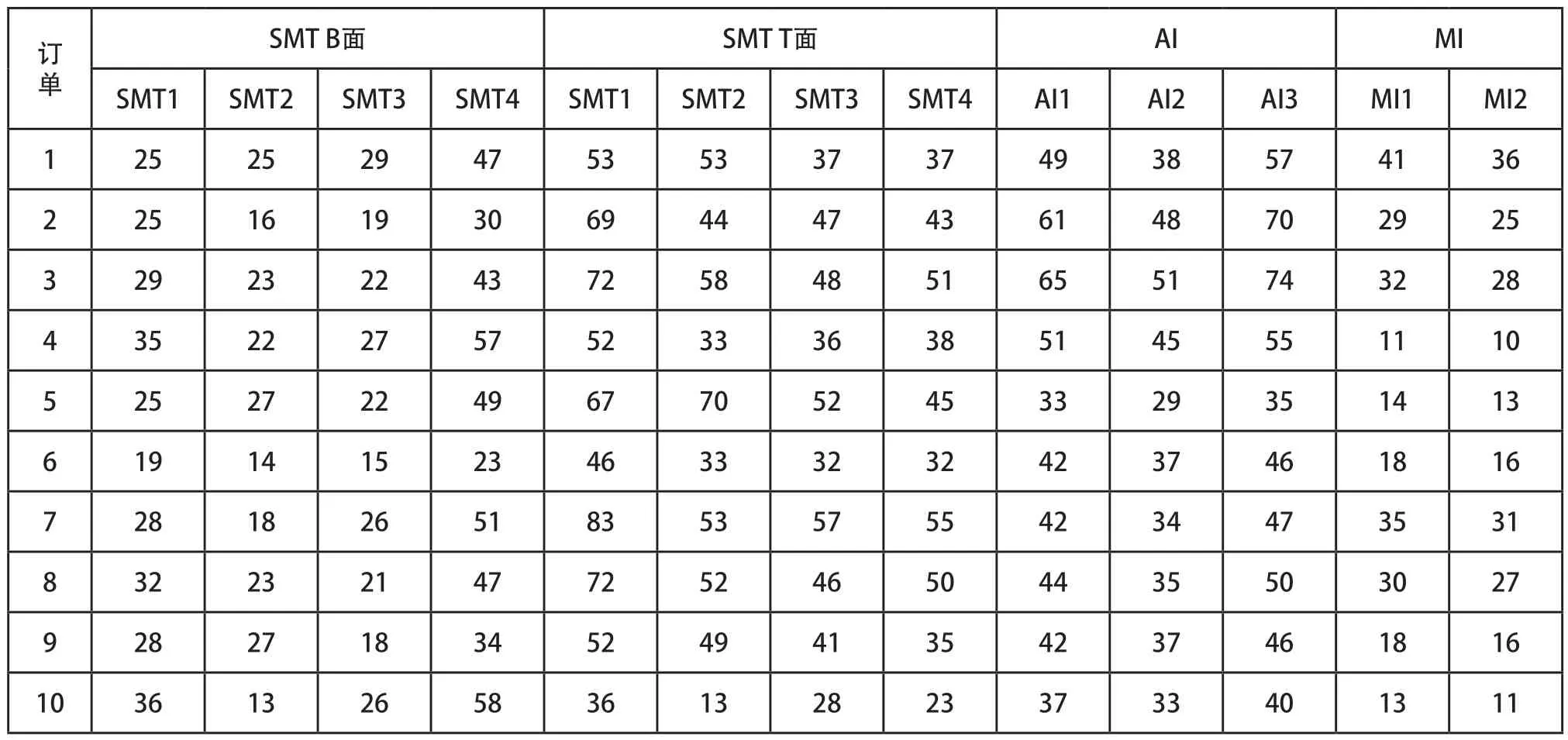
表3 PCBA车间各生产线加工时间 单位：s

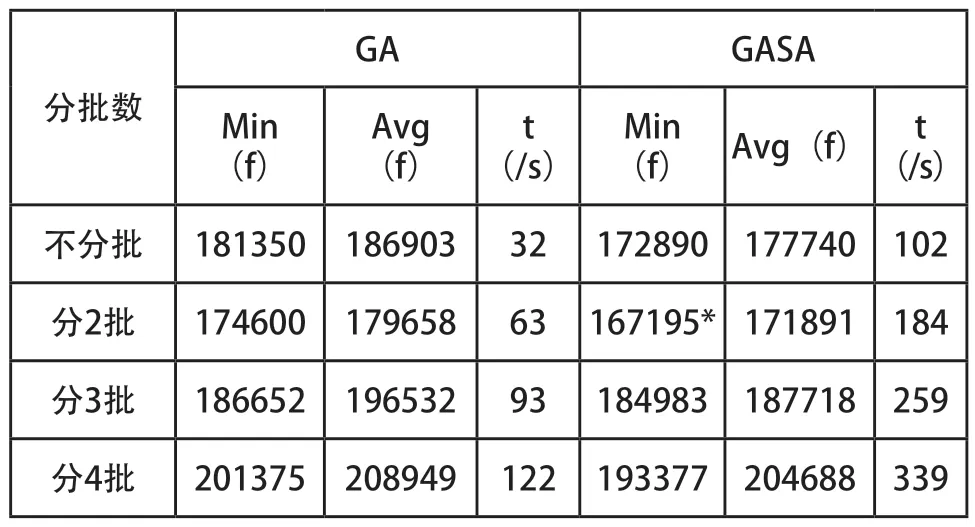
表4 GA与GASA在不同分批数中的运算结果（单位：s）

从表4可看出在不同分批数的情况下，GASA算法所得到的最优值以及平均值结果均要优于GA算法。GASA算法与GA算法相对比，Avg（f）在四种分批情况中分别减少总完工时间153min、129min、147min、71min。当分批数为2时，两种算法分别获得2910min、2787min的最优值，均优于同算法中其余分批数的结果。在GASA算法中的Min（f）值中，分2批比不分批减少总完工时间95min。

图4 GA算法在分2批情况下的搜索过程

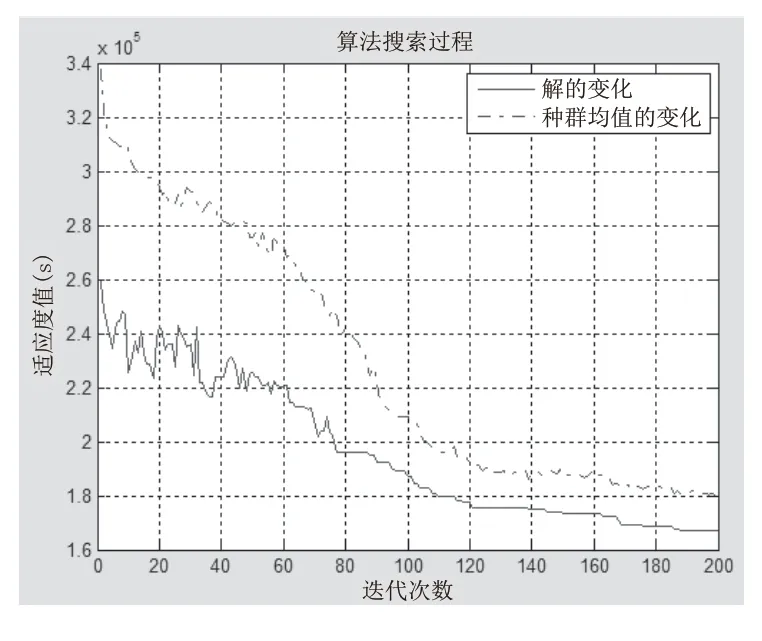
图5 GASA算法在分2批情况下的搜索过程

图6 GASA算法在分2批情况下Min（f）的调度甘特图

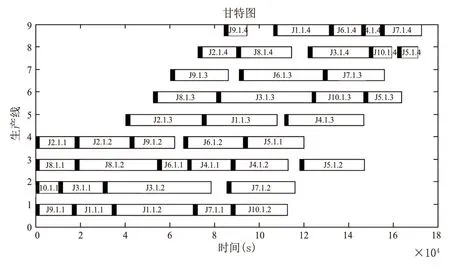
图7 GASA算法在不分批情况下Min（f）的调度甘特图

对比图4与图5，虽然GA算法全局搜索能力强，但是容易使算法的搜索过程过早地收敛，获得的最优值不佳；在GA算法中加入SA算法，有利于提高算法的局部搜索能力，避免算法的搜索过程过早地收敛。图6与图7中的黑色块为切换时间段，通过对比分析，订单分2批的完工时间要低于不分批的情况。

3.2 批量与分批次数关系分析

以实例中的10个订单种类为前提，依据随机均匀分布的方式生成各生产类型中批量范围内（如表1所示）的订单批量，采用GASA算法来求解，依次将四种生产类型的批量数据输入程序中，每种类型在不同分批情况下各运算10次，各生产类型不同分批数的运行结果与对应分批策略如表6所示。

从表6可以得出，同种生产类型，Min(f)与Avg(f)值的变化趋势具有一致性；从不同生产类型的变化趋势看，随着批量的增加，分批次数也随之增加。

4 结语

相对于传统柔性作业车间调度，各种批量生产类型下的柔性作业车间分批调度更加符合生产实际，对于现实的车间调度也更有指导意义。本文针对PCBA车间这一柔性作业车间分批调度问题，以最大完工时间最小为目标，将整个求解过程分为订单批量分批、子批排程两个阶段。通过改进算法的编码以便更好地体现分批调度问题，在交叉操作上采用洗牌与单点交叉的方式以保证获得多样化的种群个体，在变异操作上采用生产线效率偏好选择的方式以获得较低的工序加工时间，在模拟退火算法方面，引入了Metropolis接受准则，有效避免算法陷入早熟。通过实例中的算例测试与不同算法的对比分析，验证了GASA算法与批量分批策略的有效性。最后，确定了各批量生产类型下的最优分批次数，对企业各订单批量调度的分批数选择具有指导意义。但是，本文仅考虑了静态调度问题，对于动态调度未做进一步的研究，后续需要考虑更多的影响因素以保证模型更为完善。

表6 各生产类型不同分批数的运算结果与分批策略