一种转换多普勒量测的卡尔曼滤波方法∗

万 剑 芈小龙

（1.武汉数字工程研究所 武汉 430205）（2.海军装备部 北京 100076）

1 引言

在多传感器多目标跟踪系统中，直接处理多传感器问题的方法就是首先对单距离多普勒观测信息进行基于数据关联的集中式融合方法，这种方法本质上是一个多维分配问题，将会面对大量的干扰杂波的干扰，大量的干扰点会给滤波结果造成难以估计的损害[4]。当目标航迹数量很大时，这种处理方法遇到的干扰点将呈指数级增长，为后期的航迹管理带来非常大的困扰。

基于数据关联的分布式目标航迹跟踪关联处理方法是近年来受到广泛关注的一种新的处理方法[5]。雷达传感器系统提供的多普勒观测可以为滤波过程中动态模型中描述距离的部分模型提供重要的信息。所以很多学者提出了应该首先利用单传感器的距离及多普勒观测信息建立滤波模型获取某种意义上的局部航迹，消除杂波，然后利用局部航迹相关和去干扰点分级处理的方法[4]。但是基于单雷达传感器的距离及多普勒观测的相关滤波过程一般情况下会采用均匀加速度的经验模型，这种模型因为和经验的关联性很大，很难获得理想中的精度和处理效果所以通常是一个相对粗糙的运动模型[1]，例如在目标做直线运动时它的运动模型不一定满足线性演化规律而且基于对干扰的动态和静态特性上来说似然比也是不够的[4]。

鉴于此，文章中提出了一种转换多普勒测量值的卡尔曼滤波方法。这种方法摒弃了传统习惯上的用雷达传感器获取的目标径向距离、多普勒速度及其各阶微分等组成的状态向量而是用单个雷达传感器获得的目标径向距离和多普勒速度的乘积及其各阶微分以及目标的位置和方向速度组成的伪状态向量代替之，因为所构造的伪状态向量在时间上遵循线性演化规律，所以传感器提供的多普勒速度信息可以合理有效地利用以获得更丰富的目标动态特性。

2 滤波模型

式（1）是建立的跟踪目标运动轨迹模型的状态方程，该方程是建立在单部雷达独立工作所获取的数据状态之上，在整个只有距离观测和多普勒观测的多个雷达传感器多个目标存在的跟踪系统中，该状态方程是全系统建模的理论基础。

在式（1）中v（n）为系统受外界干扰时输入的高斯白噪声，在理想建模的条件下该高斯白噪声的均值应该为0。另外在建模时还应该指明系统噪声的噪声系数[2]，在这里的系数为一个和噪声向量相匹配的噪声系统矩阵Γ(n)。这里F为状态方程转换所必须考虑的状态转换矩阵，具体的形式如式（2）所示：

在状态转换矩阵中，矩阵的形式必须和预定义的状态向量的形式相匹配[3]。状态转换矩阵中最重要的参数为抽样时的时间间隔T，它决定了状态的演化过程。文章采用的状态向量的组成元素包括雷达传感器探测到的目标径向距离与多普勒速度的点乘积及其一阶微分，该状态向量在x、y方向上分解后的表达式为

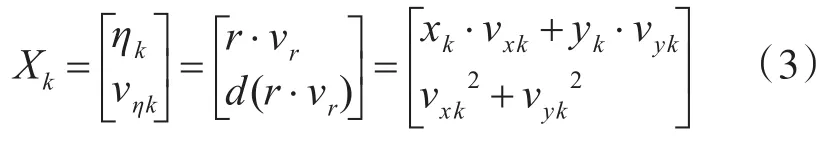
在式（3）中雷达传感器观测的目标径向距离和径向多普勒速度分别用r和vr表示，d(r⋅vr)为其一阶微分，最后一部分的内容为量测状态方程在x、y方向上分解展开后的表达形式。此处特别需要注意的是该状态向量是为了满足线性滤波条件而特殊构造的目标状态向量而不是真实目标状态的描述。

观测向量可以用式（4）来定义，这里量测值表示为雷达传感器所获取到的目标径向距离和径向速度的乘积，它不是目标真实状态的取值，所以称为伪值。

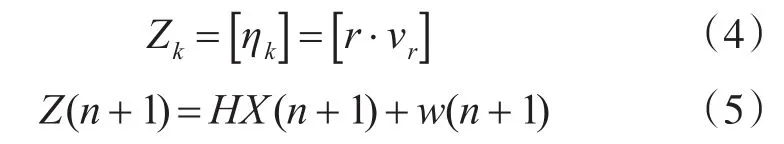
式（5）就是我们定义的量测方程，量测值定义为径向距离和径向多普勒速度的点乘积。量测方程定义为上式后，量测误差可以用式（6）获取：

进而可以得到协方差为

在式（5）中，量测转换矩阵H被定义为

建立了系统的基本模型后就可以给出系统的完整滤波过程。

状态预测方程：

协方差预测方程：

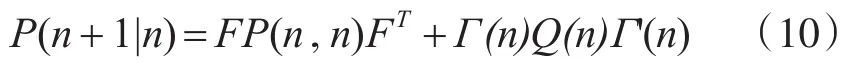
增益方程：

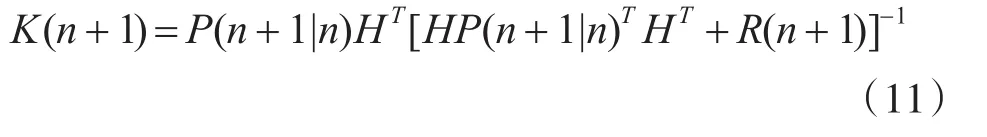
状态更新方程：

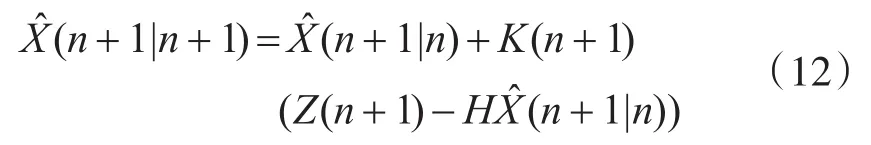
协方差更新方程：

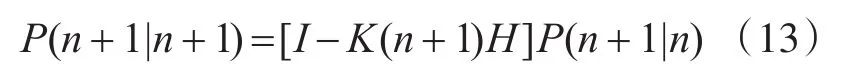
如果量测噪声的方差为R，前两个时刻的量测值为Z（0）、Z（1）则初始状态可以由式（14）来确定：

初始协方差方程：

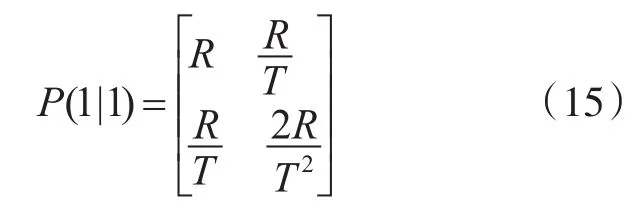
3 仿真分析

针对前文提出的转换多普勒量测的卡尔曼滤波方法，这里给出用Matlab仿真软件在实验室条件下的仿真结果。我们假设雷达传感器在直角坐标系中的位置坐标为（30km，0），跟踪目标为做匀速直线运动的目标，且其初始位置为（-10km，10km），运动速度为10m/s，运动的方向为与x轴正方向成45°夹角的方向。为了获取理想状态下的仿真结果，这里我们假设仿真环境未收到过程噪声的影响。初始状态方程为

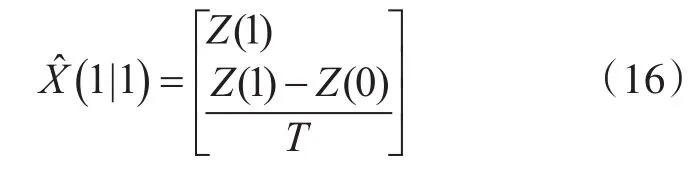
如果量测噪声的方差为r则初始状态协方差取为

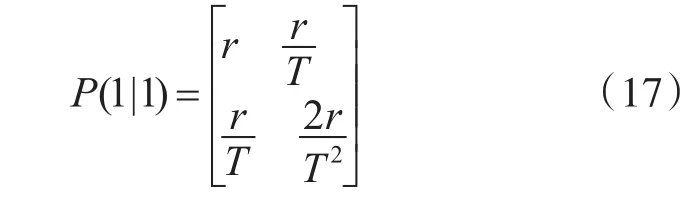
图1 转换多普勒卡尔曼滤波效果图

这里取50批样本数据，每次采样的时间间隔为t=1s，进行200次蒙特卡洛模拟，得到滤波转换多普勒速度与理想转换多普勒速度的对比图以及滤波转换多普勒速度、均方根误差和转换多普勒速度测量误差的对比图。如图1所示：

在图1中，前两个图显示滤波后的转换多普勒，以及转换多普勒速度和实际转换多普勒速度之间的比较。从图中可以看出，随着滤波次数的增加，估计值迅速收敛到实际值。在下面的转换多普勒速度和测量误差的均方根误差对比图中，滤波后的均方根误差逐渐衰减并趋于0，而预滤波后的均方根误差保持较大的波动值，说明转换多普勒卡尔曼滤波方法能有效地抑制测量杂波完成目标状态的估计。

4 结语

这篇文章主要介绍了一种转换多普勒量测的卡尔曼滤波方法。给出了转换多普勒量测滤波方法的基本理论与滤波模型，并通过Matlab仿真结果对这一滤波模型进行了仿真验证。转换多普勒量测卡尔曼滤波方法的实质是用单部雷达量测值中的跟踪目标径向距离量测和多普勒速度量测值的点乘值及其各阶微分组成一个新的状态向量，该状态向量虽然不是真实目标运动轨迹的反应，比如方程中并不包含运动目标的真实位置信息、速度信息，但是转换后的卡尔曼滤波方程却符合了线性卡尔曼滤波条件。这种方法摒弃了传统习惯上的用雷达传感器获取的目标径向距离[4]、多普勒速度及其各阶微分等组成的状态向量而是用单个雷达传感器获得的目标径向距离和多普勒速度的乘积及其各阶微分组成的伪状态向量代替之，因为所构造的伪状态向量在时间上遵循线性演化规律，所以传感器提供的多普勒速度信息可以合理有效地利用以获得更丰富的目标动态特性。通过Matlab的仿真结果表明这种滤波方法对测量噪声达到了很好的抑制作用。