数学表征：走近儿童思维的一条有效路径

杨志燕

摘 要：数学表征就是让儿童把自己的思维用图示、符号与言语等形式表达出来，它是走入儿童思维的一种重要方式。教师要精准筛选学生数学表征的作品，让儿童的表征成为他们学习的鲜活学材;引领学生深度交流，让儿童的数学表征延伸出知识的“生长点”;沟通联系，让儿童的数学表征提升知识的建构度。

关键词：数学表征;儿童思维;有效路径

中图分类号：G623.5          文献标识码：A     文章编号：1992-7711（2020）15-071-2

教师的教与学生的学总有那么一段距离，那是思维的距离。教学时教师要尽可能的贴近儿童，让儿童的思维看得见摸得着，才能更好引导儿童更真切的经历学习过程，从而帮助不同层次的儿童思维得到不同程度的发展。

怎样才能走入儿童思维，了解儿童内心真正的想法？其实最能引起儿童共鸣的往往来自儿童内心最真实的想法，让儿童把自己的思维用图示、符号与言语等形式表达出来，即数学表征，是一种走入儿童思维的重要方式。数学表征可分为内在表征和外在表征，即语言、文字、图形、符号、具体构成或实际情境等反映数学学习对象的外在形式和存在于个体头脑中而无法直接观察的心理活动的内在表征。

一、精准筛选，让数学表征成为儿童学力提升的鲜活学材

【案例1】 苏教版三年级上册《认识几分之一》教学片段

师：如果只有一个圆片你还能平均分成2份吗？每份多少个？（1/2）

师：你们知道1/2这个分数表示什么含义吗？请同学们在学习单上用你喜欢的方式写一写、画一画，表示出你对12的理解。

展示学生作品：

生1：我把一个蘑菇用刀从中间切成两半，就是1/2。

生2：我是把一个圆分成两个，一个就是1/2。

……

生3：我是把一个长方形平均分成2份，每一份就是这个长方形的1/2。

师：与上面几位同学的相比，你觉得他表示的有什么不同？

生4：我觉得他表示的很好，他用虚线表示了平均分，让人一眼就能看出来平均分成两份，而且他还把其中的一份画上了斜线，写上1/2，比上面几位同学表示得清晰。

生5：我认为不管是长方形，正方形、圆形、三角形等，只要是把一个东西平均分成2份，其中的一份就是12。

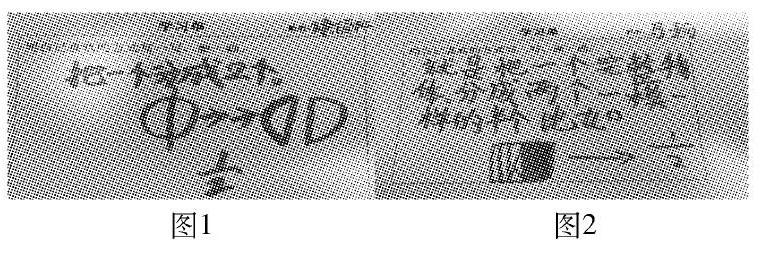
【思考】促进儿童深度思考的数学交流怎样才会真正发生？有效抽取学生表达的结果是关键的一步。这位教师到学生当中，寻找不同的表征方式，并把有代表性的作品依次呈现。学生对1/2已经有了初步的认知，不过个体理解层次还有很大差别，图1中的学生停留在把实物分成2份，每份是它的1/2;图2中的学生能抽象出一个图形，一个东西平均分成两份，每份是它的1/2，但是他用图示或文字表征时没有突出平均分。图3中的学生对1/2有了更深刻的理解，不仅用虚线表示出平均分成2份，并把其中的一份用斜线表示，可见他对1/2的理解是比较清晰的。图4中的学生对1/2的认识就更透彻，不论一个图形，一个物体只要是平均分成两份，每份就是它的1/2，所以他画了不同的图形，表示出了1/2。

案例中的这位教师大胆放手让学生用自己喜欢的方式表征对二分之一的理解，其中有图画形式，有文字形式等等。把儿童的表征作品当做数学交流的学材，通过学生的各种表征了解儿童对1/2的理解的层次是有差别的，再通过师生、同伴间的评价、交流，这样互动学习的过程就是“兵教兵”的过程，让儿童深刻理解，建立1/2的初步模型。在此过程中学生的表达方式也许简单、稚嫩，但学生用自己的水平阐述自己的理解，这样鲜活的学材更能引发儿童的共鸣，让学生亲历过程，提升他们的数学学习力。

二、深度交流，让儿童的数学表征延伸出知识的“生长点”

荷兰数学家弗赖登塔尔曾说过：“数学学习的过程就是要通过数学语言，用它特定的符号，词汇和句法去交流，去认识世界。”可见，交流是数学学习中非常重要的一部分，通过交流和同伴分享数学观点，能厘清学习过程中的困惑。

【案例2】 苏教版五年级下册《分数的意义》教学片段

老师让学生上台展示：用自己喜欢的方式表示出34。

师：他们表示的3/4有什么不同？

生：他们画的图形不一样。

生：他们平均分得物体不一样。

师：对呀！这些物体各不相同，为什么都能用3/4表示？

生：因为它们都是平均分成了4份，表示其中的3份，所以都可用3/4来表示。

这位教师通过让学生用自己喜欢的方式表示出3/4的操作活动，唤醒了学生对分数的原有认知。再利用儿童自己的表征，充分把学生的想法作为学习的资源，制造认知冲突，为什么这些物体各不相同，却都可以用四分之三表示呢？引导学生深入交流不管是一个物体、一个计量单位或许多物体组成的一个整体，只要平均分成4份，表示其中的三份就可以用3/4表示。教师抓住了知识的“生长点”“延伸点”，帮助学生抽象出对分数概念的进一步理解。

三、沟通联系，让儿童的数学表征提升知识的建构度

学生在每一节当中获得的知识都是零散的，为了使学生整体上把握知识，便于在头脑的仓库中提取和查找，数学知识最终要以结构化的方式存在于学生的头脑中。有人说课本上的知识点就像一粒粒珍珠，散乱地堆在那里是不好把握的，如果能找到一根线把它串起来，它就成了项链。随便抓住其中的哪一粒珍珠，我们都能很方便地把其它的珍珠带起来。数学表征就是那根串联的线，沟联起知识间的联系，在捕捉联系中构建知识结构，形成一张知识网。

【案例3】 苏教版六下《平面图形的面积的复习与整理》教学片段

传统的复习课教师喜欢一问一答方式，帮助学生逐一回顾知识点，最终在黑板上呈现精美的板书，看似清晰了，实则教师清晰，学生糊涂。案例3中的教师选择了3幅有代表性的学生表征的作品。图1用表格的方式呈现出平面图形计算公式及字母公式;图2整理出了公式，还清晰的整理出推导过程;图3在前2位同学的基础上，用一些线、箭头沟通了图形之间的内在联系。3位同学代表了三种不同层次的思维水平。课堂上老师让学生围绕自己的数学表征，带着想法和疑问展开充分的交流互动学习。常言道“温故而知新”，生3从图形的面积推导过程整理出了图形间的内在聯系，可谓是温故又知新。数学表征让我们离学生的思维更近，让不同的学生得到不同程度的发展。会的教不会的，层次高的教层次低的，最终达到“兵教兵”“兵强兵”的境界。其间教师要学会放手，在学生困顿处适时点拨，在优等生步伐太快时适时控一控节奏，让大家都不掉队！

（作者单位：南京市江宁区岔路学校，江苏 南京210000）