基于有限元分析的光学透镜半柔性支撑结构

邱炯捷 韩森

摘  要： 光学透镜的面形精度是影响干涉仪等光学系统性能的重要因素之一。其中光学透镜的自重是引起透镜的面形发生变化的主要原因。为了提高由光学透镜的面形精度，设计了一种具有辅助刚体的光学透镜半柔性支撑结构。通过Abaqus有限元分析软件，模拟出在半柔性支撑结构下光学透镜自重对其自身面形的影响。分析的最终结果表明：光学透镜的上表面与下表面的面形RMS值分别为3.51 nm和4.64 nm。由此可以得出，设计的具有辅助刚体的光学透镜半柔性支撑结构可以充分满足干涉仪等光学系统对光学透镜面形的精度要求。

关键词： 辅助支撑;有限元分析;光学透镜;自重变形;半柔性结构

中图分类号： TH703;TP391.77    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.08.004

本文著录格式：邱炯捷，韩森. 基于有限元分析的光学透镜半柔性支撑结构[J]. 软件，2020，41（08）：14-16

【Abstract】： The surface accuracy of optical lens is one of the important factors that affect the performance of optical system such as interferometer. Among them， the self weight of the optical lens is the main reason for the change of the surface shape of the lens. In order to improve the surface accuracy of the optical lens， a semi flexible supporting structure with auxiliary rigid body is designed. By using ABAQUS finite element analysis software， the influence of the self weight of the optical lens on its own surface shape under the semi flexible support structure is simulated. The final results show that the RMS values of the upper surface and the lower surface of the   optical lens are 3.51 nm and 4.64 nm respectively. It can be concluded that the semi flexible supporting structure of the optical lens with auxiliary rigid body can fully meet the accuracy requirements of the interferometer and other optical systems for the shape of the optical lens.

【Key words】： Auxiliary support; Finite element analysis; Optical lens; Deformation with gravity; Semi flexible structure

0  引言

隨着干涉仪技术的高速发展，对于其常规检测对象光学透镜，其自重引起的变形补偿要求也越来越高，而使用传统的压圈-隔圈固定光学透镜的方法已很难达到现如今的精度要求。并且采用仿真[1-5]的手段能够快速有效的分析各种实验。

自Yolder提出了柔性支撑的概念，便打开了柔性支撑在透镜支撑结构领域的先河[6]。武东城，高松涛，吴志会等[7]以弹性力学中薄板理论为基础的设计了一种三点挠性的光学透镜支撑结构，但三点挠性支撑受外界激励影响大，并且想要消除三叶像差依旧要经过很长时间调整，所以很难保证实际情况下的面形精度能与有限元分析时相近;彭海峰、巩岩等[8]设计了多点挠性的光学透镜支撑结构，但全柔性结构下的组件固有频率偏低影响了干涉仪等光学系统实际操作时精确度，使测量结果误差由此加大，需要靠后期相关数学方法消除误差;华洋洋，巩岩[9]设计了一种三点挠性主支撑和六点弹片辅助的光学透镜支撑结构，但没有给出主支撑和辅助支撑之间具体关系，很容易造成辅助支撑成为主支撑而导致透镜面形精度反而下降;刘悦，任田田，贾振超[10]设计了一种上方带有夹紧装置的三弹片的柔性结构，但夹紧力的存在会进一步使透镜面形收到影响。

本文研究采用半柔性支撑结构[11]提升在全柔性支撑结构下的固有频率，减少透镜干涉仪等光学系统实际运行产生振动而导致的偏移量，使测量结果更为精准，并且使透镜表面由自重带来的变形最小值可控化。

1  半柔性结构简化模型与设计

1.1  半柔性结构简化模型

如图1所示，此为本文模拟半柔性结构支撑特性所用的平凸透镜具体尺寸，透镜的直径为160 mm，透镜凸面的曲率半径为180 mm，透镜的中心厚度为30 mm，以及透镜的边缘的厚度为11.25 mm。

柔性结构采用多弹片式结构，弹片模型可简化为悬臂梁结构进行设计分析;径向采用三点挠性间隙结构（三个弹片与外结构体采用焊接）来定心并防止发生较大水平方向位移，实际操作上主要水平微调还是靠后期进行。

在不考虑柔性结构（多弹片支撑结构）与径向定位装置之间的装配夹紧力对柔性结构的变形情况下，对于支撑结构做了简化，配合简化的三点辅助刚体支撑结构组合成的半柔性支撑结构，如图2所示。

1.1.1  柔性结构，径向定位结构与辅助刚体材料选择

在材料的选择上，平凸透镜采用透明熔石英、多弹片支撑结构采用50CrVA，辅助刚体和径向定位结构采用HT200，其具体的参数如表1所示。

多弹片支撑结构在其它文献[2-4]中多采用65 Mn弹簧钢，但由于65 Mn的热过敏性导致在多弹片支撑结构在长期工作的情况下可能导致弹片挠度增大从而导致透镜的PV值和RMS值的增大。所以本文采用热过敏性比65 Mn低且屈服强度更高的50CrVA弹簧钢，也为大口径透镜的支撑实验做参考。

1.1.2  弹片个数设计

采用弹片宽度3 mm、厚度0.5 mm、以及长度（至透镜通光范围的边缘）对弹片奇数个数从3至31的多弹片支撑结构在没有使用辅助刚体的情况下使用Abaqus进行有限元仿真，输入表1的数据于简化模型的材料属性数据中，观察PV值的趋向，选取较合理的弹片个数，最终有限元分析结果如图3所示。

从图3可以观察到此平凸透镜在柔性结构的弹片数量在15之后的时候PV值变化量较小，所以设计选取15片为本文多弹片柔性支撑结构的弹片数量。

2  柔性结构挠度控制

半柔性支撑结构中的辅助刚体采用滾珠丝杠系统进行控制，要想使辅助刚体对于透镜面形的影响达到最小，就要使透镜面形的变化主要由柔性结构产生，所以就对柔性结构的挠度有一定的要求。把多弹片结构等效为多个悬臂梁结构，则从材料力学的角度可知挠度公式。

从公式（3）可知在透镜不改变，弹片数量一定时，悬臂梁的挠度大小取决于弹片的长度l，宽度b以及高度h。且和弹片长度l成正相关，和弹片宽度b以及弹片高度h成负相关。

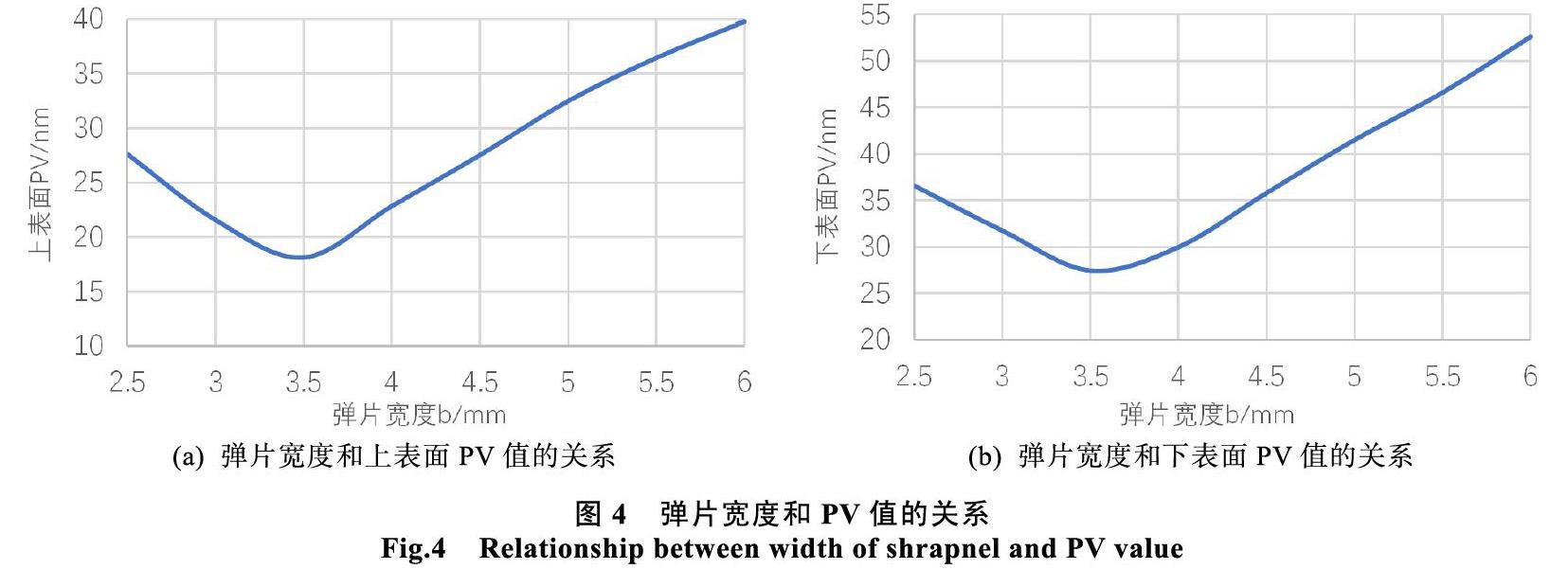
弹片支撑点（代表弹片长度）在通光范围边缘越近，则透镜的PV值越低，即透镜面形越好;弹片高度由于过高导致挠度变化量过小，所以采取机械弹片通用高度0.5 mm为宜;由于辅助刚体对于透镜面形影响较大，且一般在现有滚珠丝杠移动系统中一般最小位移为1 μm，所以辅助刚体对于透镜的位移设置在Abaqus为1 μm。则现在通过弹片宽度b来控制悬臂梁挠度，从而达到透镜面形精度最优的问题，选取弹片宽度从2.5至6 mm，依次增长0.5 mm进行有限元分析，结果如图4所示。

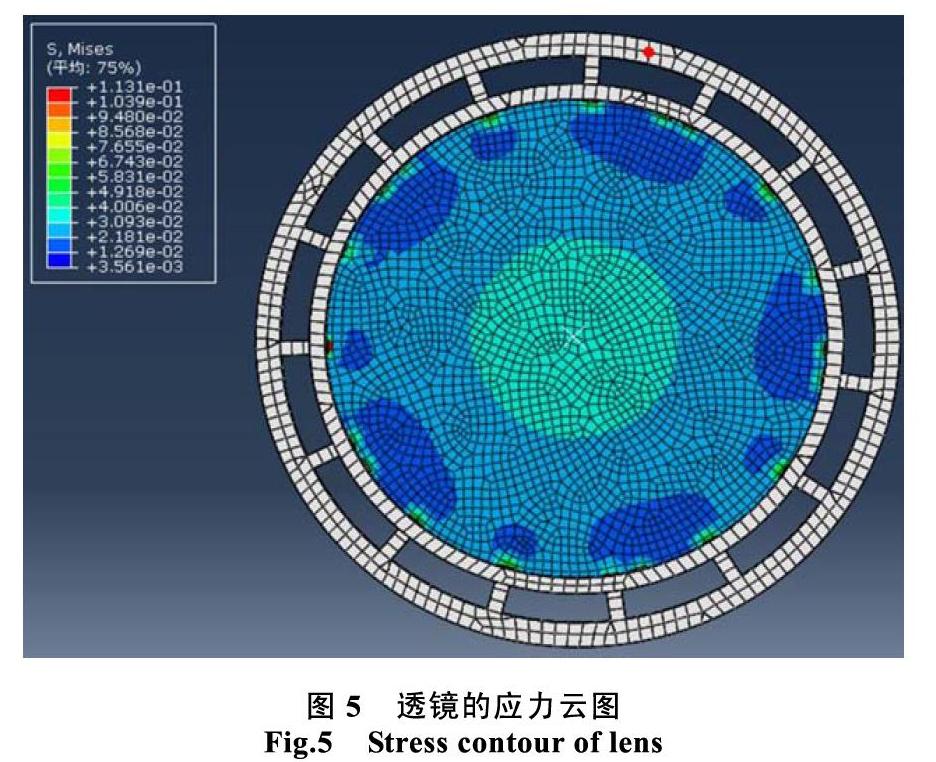
由上面两图综合可知，选取弹片宽度b为3.5左右（此处选取3.5）时可以达到最优面形精度，通过使用Abaqus提取上、下表面面形节点位移数据，使用Matlab计算得上、下表面PV值分别为18.12 nm和27.46 nm，RMS值分别为3.51 nm和4.64 nm。并且由模态理论可知，由于有辅助刚体的存在，整个结构的固有频率比纯柔性结构时候的高，可以有效缓解干涉仪测量系统运行产生的振动，从而减轻后期调整的难度和减少后期数学方法分析去除误差的复杂度。最终的透镜应力云图如图5所示。

3  结论

以设计的参数为直径160 mm、厚度30 mm的平凸透镜作为研究对像，进行一种带有辅助刚体的光学透镜半柔性支撑结构适用于光学透镜支撑的研究。研究当中着重分析了透镜重力对透镜面形精度的影响。

结果表明：基于该具有辅助刚体的光学透镜半柔性支撑结构，透镜在其自身重力影响的作用下，上、下表面面形RMS值分别为3.51 nm和4.64 nm。已知光学系统对透镜面形的精度要求（RMS<5 nm），所以设计符合要求。

由以上结论可知，研究的具有辅助刚体的光学透镜半柔性支撑结构，对光学透镜支撑具有较好的适应性，可以满足干涉仪等光学系统对光学透镜面形的要求，为进一步设计更大口径透镜的半柔性结构支撑设计提供了参考。

参考文献

[1] 陈健飞， 王云霞， 贡智兵， 等. 基于RecurDyn的城轨微动塞拉门系统动力学仿真[J]. 软件， 2018， 39（12）： 32-36.

[2] 马浩然. 基于NS3的分布式消息系统Kafka的仿真实现[J]. 软件， 2015， 36（1）： 94-99.

[3] 王连杰， 韦群. 三维云图仿真系统设计与实现[J]. 软件， 2018， 39（5）： 151-155.

[4] 张懿， 张云伟， 樊阳阳， 等. 热激励参数对管道缺陷区域热生成率影响的有限元分析[J]. 软件， 2018， 39（5）： 22-26.

[5] 王佳美， 周志尊， 胡明成， 等. 颅脑动脉瘤模型构建与计算流体力学分析[J]. 软件， 2018， 39（5）： 70-74.

[6] Yolder P R. Optical-Mechanical Systems Design[M]. Third ed. Washington： CRC Press， 2006.

[7] 武东城， 高松涛， 吴志会， 等. 高精度光学平板在三点支撑下自重变形的研究[J]. 光学学报， 2015， 35（12）： 1212001.

[8] 彭海峰， 巩岩， 赵磊. 光刻投影物镜中柔性多弹片支撑方式的性能分析[J]. 光电工程， 2013， 40（2）： 71-75.

[9] 华洋洋， 巩岩. 光刻物镜高精度挠性结构镜框设计及分析[J]. 光电工程， 2013， 40（7）： 39-43.

[10] 刘悦， 任田田， 贾振超. 单镜支撑结构对镜面面形影响的接触有限元分析[J]. 机械设计与制造， 2014， 10： 64-66.

[11] 王春林， 吕志涛. 半柔性悬挂结构分析的子结构模态法[J]. 工程力学， 2008， 25（2）： 17-21.