卷积神经网络在卫星遥感海冰图像分类中的应用探究——以渤海海冰为例

崔艳荣，邹斌,3*，韩震，石立坚，刘森

( 1. 上海海洋大学 海洋科学学院，上海 201306；2. 国家卫星海洋应用中心，北京 100081；3. 国家海洋局空间海洋遥感与应用研究重点实验室，北京 100081)

1 引言

目前用于海冰分类识别和监测的研究，无论是基于光学海冰图像还是合成孔径雷达（SAR）海冰图像，多是通过传统的监督和非监督算法，应用最多的如灰度共生矩阵（GLCM）和支持向量机（SVM）。Wang 等[1]根据GLCM 和小波纹理特征将特征空间域和频率域融合对海冰图像进行分类研究；Ressel 和Singha[2]首先进行特征提取，再输入到神经网络分类器中，并通过互信息分析了相关性和冗余度，进行海冰分类；Liu 等[3]基于SVM 算法，将后向散射系数、GLCM 和海冰密集度三者结合对海冰图像进行分类；Zakhvatkina 等[4]使用纹理特征结合SVM 区分海冰和开阔水域；Tan 等[5]通过随机森林特征选择方法确定优选特征进行海冰图像解译研究；张明等[6]采用灰度共生矩阵提取特征值，优选特征组合，结合支持向量机开展海冰类型的分类研究；任莎莎和郎文辉[7]通过高斯滤波后提取海冰图像灰度值，提出K-GMM 算法进行海冰分类；郑敏薇等[8]利用灰度共生矩阵计算并获取图像纹理，结合SVM 算法达到冰水分离的目的；逯跃锋等[9]运用灰度共生矩阵提取纹理特征中能量、对比度、相关性和同质性的特征值，结合最小距离分类算法进行海冰分类；朱立先等[10]通过灰度共生矩阵获得影像的纹理特征，利用LibSVM 分类方法对一年冰和多年冰进行训练和分类。以上的研究工作虽然都在原有的工作基础上做了改进并达到了一定的分类效果，但都需要先对遥感海冰图像进行大量且复杂的特征提取工作。面对大数据时代的今天，处理海量冗杂的海冰数据，并快速准确的提供决策支持，以上的基于传统算法的海冰识别检测方法有些捉襟见肘。

深度学习思想的本质就是通过在多层神经网络上运用各种算法来训练学习图像特征，其框架下包含多种机器学习算法，其中卷积神经网络（CNN）是目前该框架研究最深入、应用最广泛的算法。CNN 作为一个深度学习架构被提出的最初诉求，是降低对图像数据预处理的要求，避免复杂的特征工程。它可以直接使用图像的原始像素作为输入，而不必先使用算法提取特征。它的特征提取和分类训练同时进行，使得训练时就自动提取了最有效的特征，这就减轻了使用传统算法（如SVM）时必须要做的大量重复而烦琐的数据预处理工作。

目前，CNN 在图像识别、语音交互、自然语言处理等领域取得的突破和进展有目共睹。CNN 应用到卫星遥感海冰分类中的研究虽然较少，但也取得一定进展。如Wang 等[11]首次将卷积神经网络应用于海冰密集度评测中，其精度与海冰分析员手绘图相比，绝对平均误差不超过10%；Chen 等[12]使用全卷积神经网络（A-ConvNets）对海冰图像进行分类，其平均准确率高达99%，而所采用的全卷积神经网络只包含卷积层，图像经多次卷积之后尺寸越来越小，分辨率越来越低，需要通过反卷积的方式来恢复原图，过程较为复杂且部分细节仍旧无法恢复；Wang 等[13]进一步的研究发现，CNN 模型具有识别地物特征之间细微差别的能力，能够更准确地识别出新冰，然而该网络的输入要求数据经标准化处理，其处理结果直接影响后期模型的表现；黄冬梅等[14]将CNN 模型应用于海冰密集度评估和海冰分类实验中，其模型的总体分类准确率达到93%以上，Kappa 系数为0.8 以上，实验需要研究区域对应的海冰解译图作为参考标准，另外，需要先制作标签，再将样本和标签构建为one-hot 格式作为模型的输入。

本文以构建更加简洁有效的网络、简化数据集标签制作过程的原则，探索更具有适用性并可用于业务化研究的CNN 模型。以渤海海冰遥感监测为例，采用HJ-1A/B 卫星数据源，开展基于CNN 的渤海海冰遥感分类研究。渤海海冰灾害严重影响了海上运输，破坏了区域内基础设施，阻碍了油气等资源的开发与利用，加强海冰灾害监测非常必要。

2 卷积神经网络

2.1 网络结构

卷积神经网络[15]是一种前馈神经网络，是由多个阵X（S x×Sy×Sz），经K个大小为Cx×Cy×Sz的卷积核Ck，其中k=1, ···,K。每一个卷积核都会以步长P为间隔遍历矩阵，最后会得到K幅特征图，公式如下[13]：模块组成的可训练结构体，网络结构整体呈现出倒三角的形态，缓解了反向传播算法中容易出现的“梯度消失”现象。其每一个模块由3 个连续操作单元组成：卷积核、非线性转换层和池化层。一个CNN 模型通常包含多个用于提取图像特征的学习模块和若干全连接层。在卷积过程中，首先输入一个样本矩

式中，hk表示经第k个卷积核卷积后得到的输出结果；Mx,My分别为卷积操作之后输出的特征图的维度。

图1 为本研究搭建的CNN 网络主要结构，包含4 个卷积层（COV1−COV4），4 个池化层（POOL1−POOL4），3 个全连接层（FC1−FC3）。参数设置如图1 所示，所用的输入图像为 100×100×3 （其中 100×100表示图像横向和纵向尺寸，3 表示图像通道数），前两个卷积层的过滤器（filter）尺寸为 5×5，后两个卷积层的过滤器尺寸为 3×3，所有卷积层的滑动横向和竖向步长都为1，边缘填充（padding）都设置为“SAME”。池化层采用最大值池化，池化层的过滤器尺寸全为 2×2，滑动横向和竖向步长为2，边缘填充设置为“VALID”。卷积、池化后的图像尺寸如图1 所示，由下式得出：

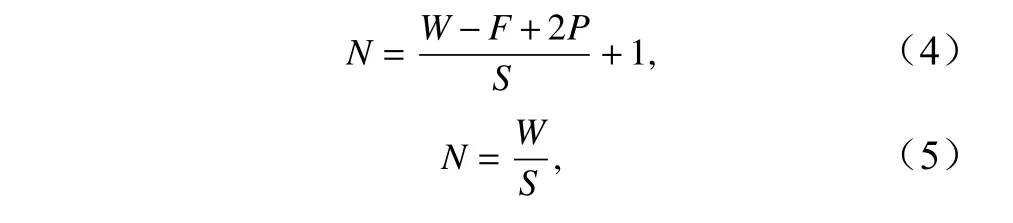
式中，N表示输出图像尺寸；W表示输入图像尺寸；F表示过滤器的尺寸；S表示步长；P表示边缘填充的参数选择，当边缘填充设置为“VALID”，输出图像尺寸用公式（4）计算，当边缘填充设置为“SAME”，输出图像尺寸用公式（5）计算。

另外，在卷积层和池化层之间都加入了激励层，通过激活函数对卷积层输出的每一个特征单元进行非线性处理，实现CNN 非线性目标可分类；全连接层放在网络的最后，与传统的全连接神经网络很相似，接收神经元要与输入层的每一个神经元连接，由此利用模型所提取到的所有特征去训练分类模型，其中第一层全连接层以卷积操作后的特征层（hk）作为输入，将特征映射表示为一个向量，并通过权矩阵W和偏置b变换到输出空间，计算公式为

式中，f为激活函数；h为网络学习后的输出结果。卷积神经网络模型训练和学习的本质就是利用输入数据的特征量调整、更新网络参数。代价函数和激活函数的选择是网络学习、参数更新、模型优化的重要环节。

2.2 二次代价函数

卷积神经网络模型训练和学习的本质就是利用输入数据的特征量调整、更新网络参数。代价函数和激活函数的选择是网络学习、参数更新、模型优化的重要环节。

神经网络为优化模型，通常采用代价函数，寻求神经网络代价函数全局最小值是一个重要而基本的问题。传统的二次代价函数[16]工作原理如下式[17]所示：

式中，C(W,b)表示网络的代价函数，也称损失函数；W、b分别表示神经网络的权值和偏置，网络训练就是通过就是不断更新权值和偏置参数来最终达到学习的目的；y(x)表示样本x的真值；y′(x)表示样本x的网络预测结果；n表示样本数量，神经网络模型的优化就是不断降低预测结果和真值的误差，使得误差最小化。结合公式（6）可看出，网络的预测值不仅和W、b有关，还与激活函数f(z)有关。在网络训练中，我们以常见的梯度下降法[18–19]来调整权值和偏置。假设有1 个样本，则W、b的推导公式为

可见W和b的梯度与激活函数的梯度f′(z)呈正比关系，当使用梯度下降法对权值参数进行调整时，随着在网络中逐层传播，残差值会变得越来越小，f′(z)的变化不仅会影响网络收敛速度，还可能引发“梯度消失”现象，致使底层网络难以进行有效训练。

2.3 交叉熵代价函数

为了消除激活函数梯度对网络权值和偏置值更新的影响，引入改进的交叉熵代价函数替换二次代价函数。交叉熵最早出自信息论中的信息熵，然后被用到很多地方，包括通信、纠错码、博弈论、机器学习等。交叉熵代价函数为

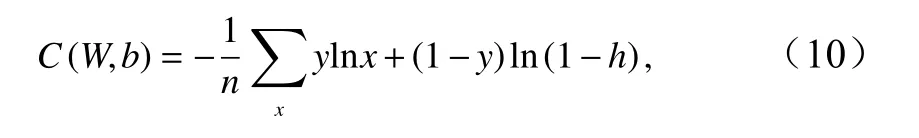
式中，C(W,b) 表示网络的代价函数；W、b分别表示神经网络的权值和偏置；y表示样本x的真值；h为公式（6）中样本x的网络输出结果；n表示样本数量。对公式（10）求偏导得到权值W和偏置b的计算公式为

可见，交叉熵代价函数中，W、b的梯度与激活函数的梯度f′(z)没 有关系，只与f(z)−y的差值，即网络输出值和真值的误差成正比，误差越大，梯度越大，参数W和b的调整就越快，网络的收敛速度也就越快，有效避免了f′(z)参与参数更新、影响更新效率的问题。

2.4 Sigmoid 激活函数和RELU 激活函数

神经网络训练的最终目的就是获取代价函数最小时的权值和偏置参数，而求取代价函数最小化过程中，激活函数的选择也起着至关重要的作用。卷积神经网络中，假设不采用激活函数，那么每一层的输出与上层的输入都是线性函数关系，不管搭建多少层神经网络，输出都是输入的线性组合，这样就局限了卷积神经网络的应用范围。因此在CNN 每个卷积层和池化层之间通常加入激励层，即通过非线性激活函数对卷积层输出的特征进行非线性映射处理，使得神经网络可以任意逼近任何非线性函数，非线性因素的引入，拓展了CNN 模型应用到更多非线性分类任务中的空间。目前常用的激活函数为Sigmoid 函数，也就是我们常称的“S”型函数，其导函数为Deriv. Sigmoid，如图2 所示。

图2 Sigmoid 原函数和导函数Deriv. Sigmoid[20]Fig. 2 Sigmoid function and Deriv. Sigmoid[20]

由2.2 节和2.3 节可知，代价函数的收敛和网络参数的调整与激活函数及其导数有关，由图2 可以看出，Sigmoid 函数取值区间为（0，1），收敛速度慢，且容易出现软饱和，即当输入较大的正数和负数的时候，梯度都为0，致使神经元参数无法更新；导函数取值从0 开始很快又趋近于0，所以网络在训练过程中容易引发“梯度消失”问题，影响网络的正常训练。

为提高网络训练效率和准确率，文中引入改进的激活函数ReLU 函数，如图3 所示，当输入为负数的时候，函数强行置0，为网络加入稀疏因素，有效降低了参数的空间相关性和依存性；当输入为正数时，函数不饱和，且梯度为1，避免了“梯度消失”现象的发生，同时网络收敛速度快，计算简单。

图3 ReLU 激活函数[18]Fig. 3 ReLU activation function[18]

3 实验验证

3.1 实验数据

实验选取HJ-1A 和HJ-1B 卫星搭载的CCD 相机获取的渤海海域2018年1月下旬至2月上旬共8 幅影像为数据源。该传感器共载荷4 个波段，具体参数如表1 所示。

表1 CCD 载荷参数Table 1 CCD parameters

本文选择B03、B02、B013 个波段，经预处理后，通过公式（13）将像元DN 值转换为具有物理意义的辐射亮度值，然后组合成真彩色RGB 图像。

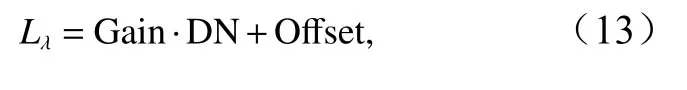
式中，Lλ表示像元辐射亮度值，它包括了物体反射的辐射能量、临近地物的贡献值，以及云层的影响；Offset和 Gain分别表示偏移和增益参数。

通过目视解译确定冰、水区域，借助MATLAB 和IDL 二次开发工具，裁剪、制作冰水样本集并加上标签，数据集共1812 个样本，分别包含812 个海冰，1000 个海水的影像样本，以8∶2 的比例分为训练集和验证集用于网络的训练和验证。模型测试部分包括覆盖渤海区域的大规模识别和随机截取一小块区域的小范围识别。大规模识别部分分别在HJ-1B 卫星2018年1月29 日图像上选取了尺寸为7824×5205 的 样 本（图4），在HJ-1A 卫 星2018年2月3 日的图像上选取了尺寸为8020×5328 的样本（图5），并以10×10、20×20、40×40 和80×80 等不同的尺寸制作测试集进行测试；小范围测试则是在图4 中随机截取一块400×400 的冰水区域作为数据源，也分别以10×10、8×8、5×5 和2×2 等4 种不同尺寸的窗口制作测试集test_10、test_8、test_5 和test_2，用于模型和参数测试。

3.2 代价函数和激活函数组合分析

本实验所用的神经网络搭建在TensorFlow 框架上，以Anaconda35.1 的Jupyter Notebook 为运行环境。首先以CNN 模型应用的经典案例—手写数字识别作为引入分析不同函数组合对识别结果的影响。试验分为二次代价函数与Sigmoid 激活函数、二次代价函数与ReLU 激活函数、交叉熵代价函数与Sigmoid 激活函数、交叉熵代价函数与ReLU 激活函数共4 个组合，每个组合分别进行8000、10000、20000次迭代，其实验结果如表2 所示。

图4 HJ-1B 卫星图像样本Fig. 4 HJ-1B satellite image sample

图5 HJ-1A 卫星图像样本Fig. 5 HJ-1A satellite image sample

对比表2 至表5 可看出，相对于二次代价函数，相同迭代次数和激活函数组合时交叉熵代价函数的训练精度和验证精度都更高，更准确；相同迭代次数和代价函数组合时ReLU 激活函数比Sigmoid 激活函数的分类精度更高，网络收敛速度更快；整体上看，对于CNN 模型在手写数字识别案例中，交叉熵代价函数与ReLU 激活函数组合训练的模型性能最好，所取得的分类精度最高，网络收敛最快。

表2 交叉熵代价函数与ReLU 激活函数组合Table 2 Combination of cross-entropy cost function andReLU activation function

表3 二次代价函数与ReLU 激活函数组合Table 3 Combination of quadratic cost function and ReLUactivation function

表4 交叉熵代价函数与Sigmoid 激活函数组合Table 4 Combination of cross-entropy cost function andSigmoid activation function

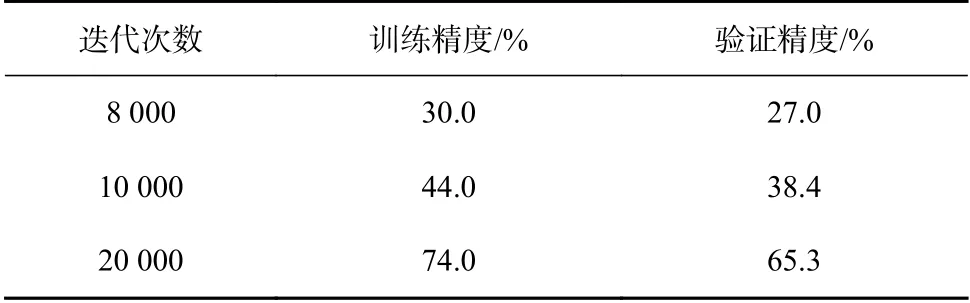
表5 二次代价函数与Sigmoid 激活函数组合Table 5 Combination of quadratic cost function andSigmoid activation function

3.3 代价函数和激活函数组合验证

由3.2 节手写数字识别案例中的结果，可看出交叉熵代价函数优于二次代价函数，ReLU 激活函数优于Sigmoid 激活函数。下面在卫星遥感海冰影像的分类识别中，进一步验证CNN 模型的最佳函数组合。首先把制作好的带标签海冰数据集以8∶2 的比例随机分为训练集和验证集，每个训练批次设置为64 个样本，迭代训练，每次迭代都会更新调整网络参数，迭代50 次后，网络权值和偏置参数基本稳定，故设置网络迭代次数为50 次。同样，将试验分为二次代价函数与Sigmoid 激活函数、二次代价函数与ReLU 激活函数、交叉熵代价函数与Sigmoid 激活函数、交叉熵代价函数与ReLU 激活函数共4 个组合。实验中发现，由于二次代价函数的权值和偏置与激活函数的梯度成正比，网络训练时，随着网络加深，残差值越来越小，导致网络无法得到有效训练，无法有效进行冰、水分离。故而，下文主要展示交叉熵代价函数与两种激活函数的组合结果。

由表6 可看出，在未对其他网络参数进行优化的情况下，交叉熵代价函数与ReLU 激活函数组合，一次性输入样本1812 个，网络迭代50 次，训练精度就达到了99.6%，验证精度达到98.4%；而对比交叉熵代价函数与Sigmoid 激活函数组合的模型，其验证精度就高出17.6%。可见，交叉熵代价函数与ReLU 激活函数组合在渤海海冰图像分类任务中精度更高、效果更好、具有更好的适应性。

表6 不同代价函数和激活函数组合的海冰图像分类结果Table 6 Sea ice image classification results with different cost function and activation function combinations

图6 和图7 为通过TensorFlow 框架下的可视化工具TensorBoard 直观地展示的交叉熵代价函数和ReLU 激活函数组合进行渤海海冰图像分类实验过程中网络训练精度和误差损失变化情况。由图可以看出，随着网络训练次数增加，网络训练误差趋近于0，分类精度趋近于1，说明交叉熵代价函数和ReLU激活函数组合训练的CNN 网络收敛速度快，分类效果好。将该训练好的网络模型和参数保存，分别利用test_10、test_8、test_5 和test_2 样本集进行测试，调用模型和参数得到的识别结果中，鉴于 8×8窗口制作的样本，其分类结果与 10×10窗口制作的样本分类结果较为相似，区分度不高，故本文只展示了10×10、5×5、2×23 种尺寸窗口的分类结果，如图8 所示。

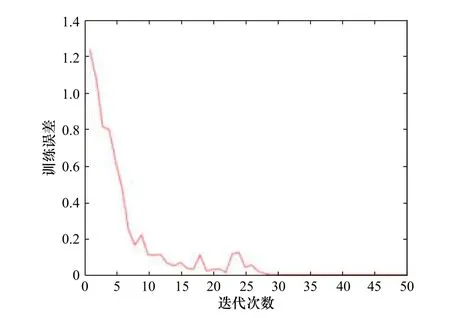
图6 模型训练误差曲线Fig. 6 Loss curve ofmodel training

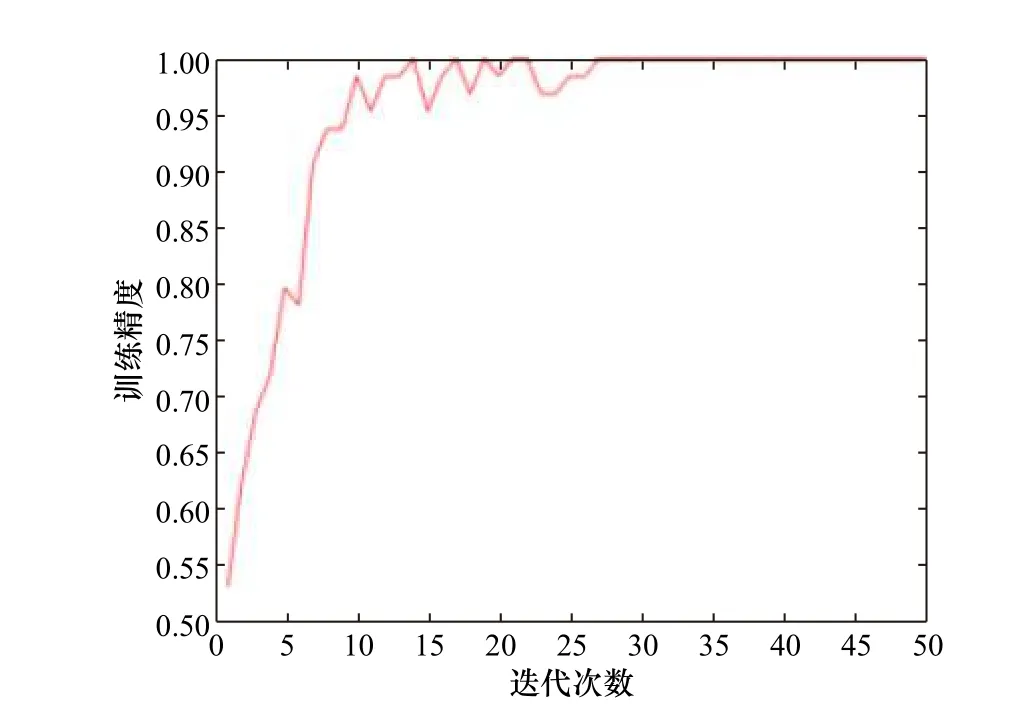
图7 模型训练精度曲线Fig. 7 Accuracy curve ofmodel training

图8b至图8d可看出在一定范围内随着样本窗口减小，模型识别结果更加准确，且在细节上表现更加精准，所以2×2窗口制作的样本分类测试结果最佳；对比图8a 和图8b，可以看出红色框出区域肉眼较难察别的部分海冰，被该CNN 模型清晰准确的区分出来，黄色框出区域表示在冰水混合的状况下，模型较好的区分海冰和海水，并将冰间水分离出来。可见CNN 模型具有识别地物特征之间细微差别的能力，在卫星遥感图像冰水解译中也适用，且表现较好。

3.4 CNN 模型对整个渤海海域的海冰识别结果分析

3.3节通过对较小区域冰水识别结果的展示和分析，证明了CNN 网络模型在卫星遥感海冰图像分类中具有较好的适用性和可操作性。为了能够将CNN 模型更广泛、切实地应用到卫星遥感海冰影像分类任务中，本文尝试将整个渤海海域作为输入数据集，希望实现大范围海域的海冰识别，能够为海域监测、航道监测和航线设计提供一些帮助。

对图4 数据源以 10×10窗口制作样本406640 个，20×20窗 口制作样本101660 个，40×40窗口制作样本25350 个，80×80窗口制作样本6305 个。分析发现窗口 10×10和 20×20所得结果没有明显差异，而数据量相差巨大，工作量巨大，故舍弃。本文主要展示其他3 个窗口尺寸的结果（图9）。为了进一步验证模型的有效性和适用性，将图5 作为数据源做同样的操作，其中以 20×20窗 口尺寸获得106666 个样本，40×40窗口获得26600 个样本，80×80窗口获得6600 个样本，模型识别的结果如图10。由图可见，随着窗口尺寸的增大，图像分辨率越来越低，识别结果越来越粗糙，但整体上3 种窗口的识别分离效果都较好，与目视结果基本一致。并且在图9a 和图10a 中黄色框所示的小范围区域，模型可较为准确地区分冰间水和水间冰，再次验证了CNN 模型在识别地物特征细微差别的能力。

在实际的应用中，可根据不同的任务需求和研究区域规模，调整样本采集的窗口尺寸。如研究海冰分布特征，需要研究日尺度海冰面积和覆盖度变化，则需要较高准确率的海冰识别结果，再如进行关于航道规划的研究，需要把握冰情和航线安全状况，希望得到分辨率较高的信息，这些情景下都可根据需要选择20×20及以下的窗口；如果研究长时间序列海冰演变和海冰外缘线变化，选择 40×40大小的窗口就可以很好的拟合海冰分界线，提供较为准确的信息；然而，当只需要把握整体海域的结冰状况时，可考虑选择80×80左右的窗口，工作量小，操作简单，可快速提供大范围冰情信息。

图8 模型测试样本400×400 数据源（a）和2×2（b）、5×5（c）、10×10（d）窗口大小模型识别结果Fig. 8 Test sample 400×400 (a), and 2×2 (b)、5×5 (c)、10×10 (d)model recognition resultsa 中亮色为海冰，暗色为海水；b−d 中紫色代表海冰，黄色代表海水The bright represents sea ice, and the dark represents sea water in a；the purple represents sea ice, and the yellow represents sea water in b-d

4 结论

本文将CNN 模型应用于海冰图像进行冰、水分类的初步探索，验证了该网络模型在处理卫星遥感海冰图像的可行性，可作为之后将深度学习网络模型应用于海冰研究、海域监测、航道监测等的理论参考。

本文首先通过CNN 模型进行手写数字识别实验讨论了代价函数与激活函数组合对分类结果的影响。基于迁移学习的思想，甄选交叉熵代价函数作为目标函数通过分别与Sigmoid 激活函数和ReLU 激活函数组合对渤海海冰图像进行分类识别，对比得出交叉熵代价函数和ReLU 激活函数组合分类效果更好，精度更高，对遥感海冰图像分类具有更高的适应性。从测试样本集的识别结果发现，当分类模型确定时，样本采集窗口的尺寸也是影响模型识别结果的重要因素，在 400×400小范围识别实验中最佳窗口尺寸为2×2，冰水分离效果较好；在整个渤海海域的识别实验中，展示了3 种不同窗口尺寸的识别结果，整体上都较好，与目视解译基本一致。最后又对不同尺寸在实际操作中的应用进行了讨论，可根据任务需要，研究区域尺度、遥感图像分辨率等，相应调整样本采集的窗口尺寸，以达到预期目的。

CNN 网络模型特征学习能力较强，学习速度快，且具有较好的可移植性，其无需提前进行特征提取，直接进行图像输入的特性，避免了大量且复杂的特征提取工作，为之后大规模进行多种冰型分类和不同冰型混合的复杂分类任务，以及海冰要素反演等研究工作提供一个新思路。

图9 HJ-1B 卫星图像20×20（a）、40×40（b）和80×80（c）窗口大小模型识别结果Fig. 9 20×20 (a)、40×40 (b)、80×80（c）model recognition results of HJ-1B satellite image红色曲线表示冰、水分界线The red curve represents the ice-water boundary

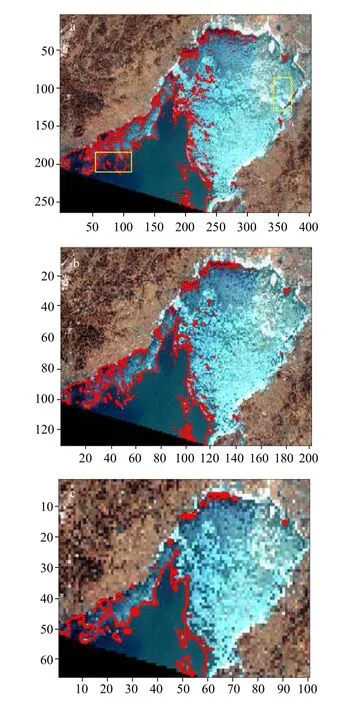
图10 HJ-1A 卫星图像20×20（a）、40×40（b）和80×80（c）窗口大小模型识别结果Fig. 10 20×20 (a)、40×40 (b)、80×80（c）model recognition results of HJ-1A satellite image红色曲线表示冰、水分界线The red curve represents the ice-water boundary