单股钢丝绳丝间多层耦合接触性能研究

(重庆交通大学交通运输学院，重庆，400074)

钢丝绳具有强度高、质量轻、柔韧性好和材料利用率高等特点，广泛应用于起重机械、矿山设备和悬索桥等工程领域。作为工程机械的重要部件，钢丝绳在服役期间长期受到拉伸、扭转和弯曲等复杂的载荷作用，尤其在恶劣应用环境中，其承载能力恶化直接影响安全生产，因此，研究其服役性能显得至关重要。至今，国内外学者广泛研究了钢丝绳。

早期研究大多基于线弹性假设，主要采用半连续模型和离散模型[1]，研究方法主要包括理论解析法、有限元法、半解析法及试验等。USABIAGA等[2]忽略泊松比效应和接触变形，根据递归法研究一次及二次螺旋线在拉伸和扭转载荷下的轴向力学性能；ARGATOV[3]建立了一种简单螺旋钢丝绳股离散模型，并分析了泊松比和接触变形影响下的钢丝绳股丝间接触行为；ZHANG等[4]基于解析法研究了三股螺旋钢丝的接触变形和摩擦性能，发现丝间摩擦显著影响接触变形；WANG等[5]基于包络理论建立了包络线的数学优化模型；XIANG等[6-7]和张曼曼等[8-10]分别研究了钢丝绳股轴向力学性能，均指出钢丝绳股的接触性能与捻角有关。随着计算机技术和有限元理论的发展，也有许多学者采用有限元方法仿真分析钢丝绳。JIANG等[11-13]根据钢丝绳股的几何特征和相应边界条件，建立了具有较高计算效率的单股钢丝绳有限元模型，但该模型因其复杂的节点约束方程而未被推广；王大刚[14]通过有限元法，研究了1×19 钢丝绳股在不同工况条件下的响应、应力分布和变形情况，得到静轴向拉伸作用下丝间相对位移、拉力和丝间接触应力；张敏等[15]对6×36 WS-FC 钢丝绳进行了有限元分析，指出交互捻钢丝绳股性能优于同向捻；马军等[16-17]对6×7 的IWS钢丝绳进行有限元分析，发现同向捻制钢丝绳应力及变形的变化幅度明显比交互捻钢丝绳的高；刘玉辉等[18]建立了单捻钢丝绳有限元模型，发现钢丝间的点接触导致了钢丝应力周期性波动；GHOREISHI 等[19]比较现有钢丝绳理论模型与有限元模型，发现捻角小于20°时两者结果基本一致，捻角大于20°时两者结果差异较大。以上研究为钢丝绳的理论研究提供了有益参考，然而早期研究大多忽略了涉及复杂非线性问题的丝间接触变形因素，而近期研究对此虽有考虑，但仍缺乏关于丝间多层耦合接触性能的深入探索。此外，在一些工程应用中，具有螺旋结构特征的钢丝绳因承受扭转载荷而发生丝间挤压，挤压区产生较大的接触变形和局部应力集中，严重时可能导致应力屈服和接触疲劳等现象。

为此，本文综合考虑钢丝绳的泊松比效应和接触变形等非线性因素，建立具有多层结构的单股钢丝绳丝间多层耦合接触特性与轴向力学性能模型。采用共轭梯度法(CGM)和快速傅里叶变换(FFT)等数值方法[20]，实现不同层间钢丝接触特性的耦合求解，并分析钢丝绳结构参数与扭转应变对其性能的影响，以期为具有多层结构的单股钢丝绳设计和应用提供理论依据。

1 理论建模

基于COSTELLO[21]研究的理论对承受轴向载荷作用的单股钢丝绳进行理论建模。图1所示为多层结构单股钢丝绳几何特征，由图1可见：本文所研究的单股钢丝绳由1 根直芯丝、6 根右捻螺旋内层钢丝和12 根左捻螺旋外层钢丝组成。其中，芯丝、内层和外层螺旋钢丝分别由“cw”，“mw”和“ow”表示，芯丝、内层和外层螺旋钢丝的初始半径分别由Rc，Rm和Ro表示，rm和ro分别表示变形前内层和外层螺旋钢丝轴线的螺旋半径。加载后各变量的值由对应含有“—”的符号表示。

图1 多层结构单股钢丝绳几何特征Fig.1 Geometric features of single-strand wire rope with multi-layer structure

1.1 螺旋钢丝几何表征

本文研究的单股钢丝绳螺旋钢丝轴线属一次螺旋线，加载前后的螺旋钢丝几何特征如图2所示。其中，αs，θs，lps，Ls和ls(s=m、o，分别表示内层螺旋钢丝和外层螺旋钢丝，下同)分别为加载前螺旋钢丝的捻角、螺旋角、捻距、轴线长度及其沿整绳轴向的投影弧长。此外，工程常用的钢丝材料(如碳钢等)在丝间挤压载荷达到一定量级时，丝间接触会引起塑性变形，但小载荷工况下可将钢丝视作弹性[1,19,22]。因此，本文基于线弹性假设，考虑单股钢丝绳多层丝间接触变形和泊松比效应，对轴向扭转载荷作用下的单股钢丝绳进行理论建模。

图2 螺旋钢丝加载前后几何特征Fig.2 Geometric features of spiral steel wire before and after loading

轴向扭转载荷作用下，单股钢丝绳的总拉伸应变εt及扭转应变τt分别为

式中：l为单股钢丝绳初始长度；Δφ为钢丝绳两端面的相对转动角位移。

变形前内层与外层螺旋钢丝轴线的初始螺旋半径rm和ro分别为

考虑泊松比效应和接触变形引起的扁平效应，则变形后内层与外层螺旋钢丝的螺旋半径分别为

轴向扭转载荷作用下，单股钢丝绳芯丝轴向拉伸应变等于钢丝绳总应变，即ξc=εt。而内层和外层螺旋钢丝轴向拉伸应变ξs和变形后的螺旋角为

考虑接触变形对单股钢丝绳内层和外层钢丝螺旋角及螺旋半径的影响，则变形前后内层和外层螺旋钢丝曲率、挠率的变化量为

式中：κs和κ′s分别为变形前螺旋钢丝轴线上任一点处主法向和副法向的曲率；τs为该点处的挠率。其中，螺旋钢丝轴线在某截面处的主法向和副法向和切向分别以x，y和z表示。

1.2 螺旋钢丝受力平衡方程

将单股钢丝绳内层及外层螺旋钢丝视作弹性曲杆，轴向载荷作用下，内层和外层螺旋钢丝的受力平衡方程为

式中：N′s为螺旋钢丝截面处所受的沿着y方向的剪切力；Ts为螺旋钢丝截面处所受的沿着z方向的拉力；G′s为螺旋钢丝截面处所受的关于y轴的弯矩；Hs为螺旋钢丝截面处所受的扭矩；Xs为单位长度内外层螺旋钢丝轴线所受的沿螺旋钢丝主法线方向的线载荷。

假设单股钢丝绳处于线弹性范围，则螺旋钢丝截面的轴向拉力、弯矩和扭矩为[23]EIs(Δκs+κ′sξs)，Hs=GJs(Δτs+τsξs)。其中，Es为螺旋钢丝的弹性模量；为变形后的螺旋钢丝横截面积。

本研究仅考虑单股钢丝绳不同层钢丝间的接触而忽略同层钢丝间的接触，由于接触变形量很小，仅考虑泊松比效应并忽略接触变形对钢丝横截面积的影响[3,12,24]，即EIs和GJs分别为螺旋钢丝的抗弯刚度和抗扭刚度。

1.3 丝间多层接触建模

单股钢丝绳丝间接触模型如图3所示，图3中芯丝与内层螺旋钢丝间的接触为线接触，接触区为具有一定宽度的空间螺旋区域，定义该区域的中线为名义接触线nmc；内层和外层螺旋钢丝间的接触为点接触，定义内外层螺旋钢丝上的点接触区中心连线分别为各自钢丝的名义接触线nmo和nom。

图3 单股钢丝绳丝间多层接触模型Fig.3 Contact between multiple layers of single-strand wire rope

假设芯丝与内层螺旋钢丝接触线及内层和外层螺旋钢丝接触线均为一次螺旋线，则接触线nmc，nmo和nom的螺旋角和分别为：和其中，接触线螺旋半径为

如前所述，单股钢丝绳芯丝与内层螺旋钢丝接触为狭长的线接触区域，为便于推导，沿接触线方向取无穷小长度ds的芯丝、内层螺旋钢丝接触段，二者在该段内的接触载荷为Fmc=dsXcmc，其中，Xcmc为单位长度接触线nmc所受的线接触载荷；内层和外层螺旋钢丝接触区域则呈现离散的点状分布，接触点处受到的点接触载荷Fom为

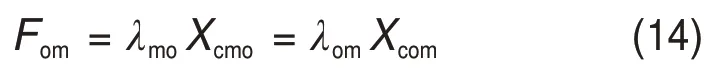
式中：Xcmo和Xcom分别为单位长度接触线nmo和nom所受的线接触载荷；λmo和λom分别为接触线nmo和nom上2个相邻接触点间的距离。不考虑同层相邻螺旋钢丝间接触，根据接触线与螺旋钢丝轴线的几何关系，确定单位长度接触线所受接触载荷Xcmc，Xcmo和Xcom与单位长度螺旋钢丝轴线所受的沿钢丝主法向线的载荷Xmc，Xmo和Xo的关系为

内层螺旋钢丝单位长度线载荷Xm可视为分别来自芯丝与外层螺旋钢丝作用力的合力

图4所示为内层与外层螺旋钢丝相邻两接触点的位置关系，线段AC和DF分别为内层与外层螺旋钢丝的接触线，点G和H为接触线上2个相邻接触点。

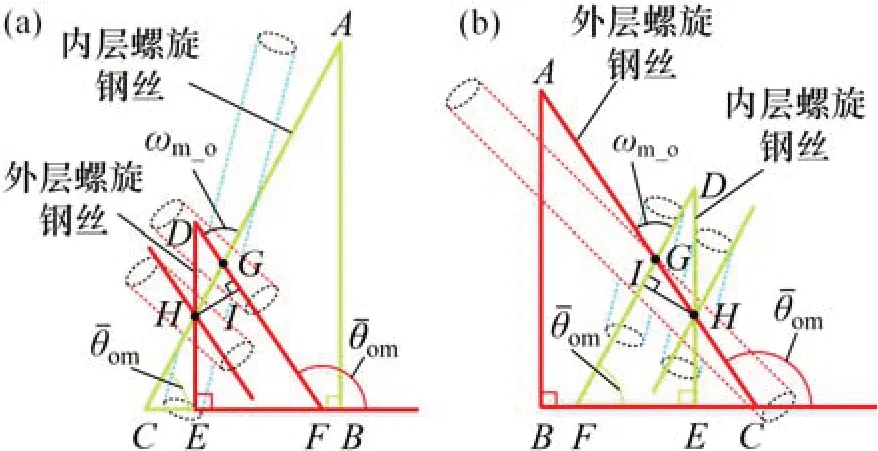
图4 内层和外层螺旋钢丝间接触关系Fig.4 Contact relationship between middle layer and outer spiral wires

根据图4中几何关系可知，内层和外层螺旋钢丝在接触线上两接触点间的距离λmo和λom分别为

式中：Ac为丝间接触区域。轴向载荷作用下，单股钢丝绳丝间接触间隙h为

式中：h′为初始接触间隙；u为丝间接触总变形；e为丝间接触区弹性变形引起的钢丝径向相对趋近位移。由于丝间接触面积远小于钢丝尺寸，因此可采用BOUSSINESQ公式[25]计算弹性变形

式中：Gu为接触压力对弹性变形的格林函数。

丝间接触区的接触压力非负而接触间隙为零。

而非接触区则相反，

复杂的多层丝间耦合接触将引起单股钢丝绳的内部应力，严重时可能引起应力屈服等。基于线弹性假设，钢丝内部弹性应力σςζ为

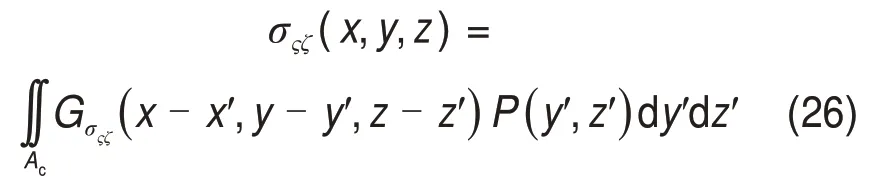
式中：ς和ζ表征应力分量方向，取值分别为ς=x，y，z和ζ=x，y，z；Gσςζ为表面接触压力对钢丝内部弹性应力的格林函数。

2 数值求解

对于本文所建立的考虑泊松比效应及丝间多层耦合接触因素的单股钢丝绳力学性能模型，其求解方案总体流程如图5所示，具体过程如下：

1)假设内层与外层螺旋钢丝间的总变形量为，初始变形量为0 μm；

2)假设芯丝与内层螺旋钢丝间的总变形量为，初始变形量为0 μm；

3)计算内层螺旋钢丝轴向拉伸应变和变形后的螺旋角及螺旋钢丝截面的轴向拉力、弯矩和扭矩，求解内层螺旋钢丝受力平衡方程式，进而计算芯丝与内层螺旋钢丝接触载荷；

4)求解芯丝与内层螺旋钢丝接触模型，计算芯丝与内层螺旋钢丝间的总接触变形量δmc；

6)计算外层螺旋钢丝轴向拉伸应变和变形后的螺旋角及螺旋钢丝截面的轴向拉力、弯矩和扭矩，求解外层螺旋钢丝受力平衡方程，进而计算内层与外层螺旋钢丝接触线载荷；

7)求解内层与外层螺旋钢丝接触模型，计算内层与外层螺旋钢丝间的总接触变形量δmo；

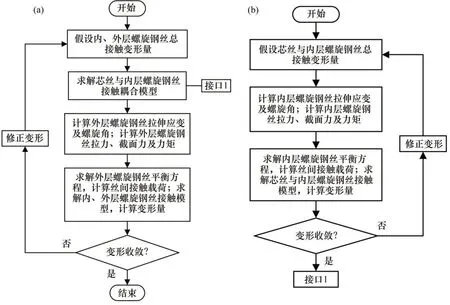
图5 单股钢丝绳多层接触模型求解流程Fig.5 Solution process for multi-layer contact model of single-strand wire rope

上述求解流程的关键在于丝间接触模型的求解。针对接触压力与弹性变形间存在的相互耦合关系，本研究采用共轭梯度法(CGM)实现丝间接触压力与接触变形的同步求解。由于迭代中需要反复计算弹性变形和钢丝内部应力，传统的直接累加法(DMM)非常耗时[26]。对此，本文采用半解析法(SAM)实现上述变量的快速求解：首先，通过解析方法计算得到接触压力对弹性变形及钢丝内部应力的影响系数；其次，采用基于快速傅里叶变换(FFT)的混合算法实现变形及钢丝内部应力的快速计算[27]。

3 模型验证

本文采用COSTELLO[21]理论对单股钢丝绳丝间多层耦合模型进行验证。其中，取多层结构单股钢丝绳参数为：Rc=1.97 mm，Rm=1.865 mm，Ro=1.865 mm，αm=αo=10°，Ec=Em=Eo=197.9 GPa，νc=νm=νo=0.3，εt=0，τt=10 rad/m。最终，芯丝与内层螺旋钢丝间总变形量及内层和外层螺旋钢丝间总变形量的迭代收敛值(扭转应变为10 rad/m时)分别为6.56 μm和12.38 μm。

图6 单股钢丝绳耦合数学模型验证Fig.6 Verification of coupling mathematical model for single-strand wire rope

上述条件下，本文模型的计算结果与Costello理论计算结果比较如图6所示。由图6可知：在载荷较小时，二者结果高度吻合，而在载荷较大时存在一定差异。上述差异是由于本模型考虑了钢丝间的接触变形而Costello模型未予考虑，且扭转载荷增大加剧了丝间接触作用，导致二者差异随载荷增大而增大。综上所述，二者结果总体较好吻合，本文所建立的模型可实现单股钢丝绳力学性能的有效求解。

4 结果与讨论

4.1 多层耦合接触界面性能

不同轴向扭转载荷作用下，单股钢丝绳局部界面接触性能参数三维分布如图7所示。其中，内层和外层螺旋钢丝捻角均为10°。需要说明的是，本研究采用等长度扭转方式实现扭转载荷的施加，即令两端面间的相对轴向拉伸应变εt=0，扭转应变τt=10 rad/m，同时扭转载荷方向与内层螺旋钢丝捻向相同。由图7可知：在轴向扭转作用下，单股钢丝绳线接触和点接触区域的接触压力与接触变形均呈现相似的变化规律，最大接触压力与接触变形均出现在接触区域中心，且点接触区域处的最大接触压力与接触变形明显高于线接触区域。可见，随着轴向扭转载荷持续增加，内层和外层螺旋钢丝间的接触区域最易发生应力屈服等现象。

不同螺旋钢丝捻角下单股钢丝绳丝间多层接触性能的演变如图8所示。由图8可见：不同层钢丝间的接触压力和变形随着扭转呈现出显著不同变化趋势。芯丝与内层螺旋钢丝间的接触压力和变形均随扭转应变增大而增大，且增大率逐步减小，在扭转中后期呈近似线性增长趋势。而内外层螺旋钢丝间的接触压力与变形的变化则有所不同，其大致呈先增大后减小的趋势。上述接触性能的演变差异是由单股钢丝绳的螺旋结构以及内外层螺旋钢丝捻角不同造成。

图7 轴向扭转载荷下单股钢丝绳丝间多层耦合接触界面性能Fig.7 Interfacial behavior of multi-layer coupling contact for single-strand wire rope subjected to an axial torsion

图8 螺旋钢丝捻角对单股钢丝绳丝间多层耦合接触性能演变的影响Fig.8 Influence of layer angles on multi-layer coupling contact behavior evolution of single-strand wire rope

相同扭转载荷作用下，外层螺旋钢丝捻角较大的单股钢丝绳，其芯丝与内层螺旋钢丝间、内-外层螺旋钢丝间的接触压力与变形均较大。然而，内层螺旋钢丝捻角增大反而减小了内外层螺旋钢丝间的接触变形，可见内外层螺旋钢丝捻角的变化对单股钢丝绳丝间多层接触性能具有不同影响。图8结果还表明：内外层螺旋钢丝间的点接触强度并非始终高于芯丝与内层螺旋钢丝间的线接触强度，对于承受较大扭转载荷且外层螺旋钢丝捻角较小的单股钢丝绳，其芯丝与内层螺旋钢丝间的接触作用更强。由此可知，在钢丝绳的设计与应用中，应充分考虑结构参数和载荷参数对其服役性能的影响。

4.2 多层耦合接触区特征

螺旋钢丝捻角对单股钢丝绳耦合接触界面性能的影响差异是由丝间接触区特征的不同而引起，如图9所示。其中，对于点接触，其接触区为椭圆形(特殊情况下为圆形)，对应的接触区域特征尺寸参数为长半轴a与短半轴b，图9中aHz为等效接触半径，定义为由图9可知：所有接触区域的几何参数及层间接触力随外层螺旋钢丝捻角增大而增大，而内层螺旋钢丝捻角增大导致了内外层螺旋钢丝间接触参数减小和芯丝与内层螺旋钢丝间接触参数增大。结合图9(a)和(c)可见：同一螺旋钢丝捻角下，内层和外层螺旋钢丝的等效接触半径aHz_mo明显高于芯丝与内层螺旋钢丝接触半径bcm。由此可见，在实际的使用中，为均衡不同接触界面处的扁平效应及磨损速率，宜选用外层螺旋钢丝捻角较小或内层螺旋钢丝捻角较大的钢丝绳。

图10所示为不同螺旋钢丝捻角下的内外层螺旋钢丝接触区域尺寸演变。由图10可见：随着扭转加载，内层与外层螺旋钢丝间接触区域长半轴和短半轴总体呈非线性变化规律，二者均有先增大后减小的趋势。同时，相比于短半轴，长半轴的变化对螺旋钢丝捻角更为敏感。随着外层螺旋钢丝捻角增大，长半轴和短半轴均增大，而由于长半轴变化更为剧烈，导致半轴比率随之增大；内层螺旋钢丝捻角对长半轴和短半轴的影响则有所不同，该捻角增大将引起长半轴减小和短半轴增大，因而半轴比率也随之增大。可见，在单股钢丝绳的实际应用中，较小的内层和外层侧丝捻角有望降低内层与外层螺旋钢丝间的接触面积，降低摩擦磨损。

图9 轴向扭转载荷下的丝间接触区域几何参数及接触力Fig.9 Geometric parameters and contact forces of inter-wire contact area subjected to axial torsion

4.3 多层耦合接触次表面性能

轴向扭转载荷作用下，单股钢丝绳丝间多层耦合接触引起的钢丝内部应力分布如图11所示。由图11可知：芯丝与内层螺旋钢丝间、内外层螺旋钢丝间接触引起的内部应力均随接触深度增大而呈先增大后减小的趋势，且最大内部应力始终发生在距离接触表面一定深度处。可见，若考虑钢丝弹塑性并对钢丝绳施加较大的扭转载荷，则该区域将首先发生应力屈服和塑性变形。

随着螺旋钢丝捻角增大，最大内部应力逐渐增大，且发生区域愈加远离接触表面。然而，不同接触界面下的内部应力变化受螺旋钢丝捻角变化的敏感程度有所不同。对于内外层螺旋钢丝接触引起的内部应力，其分布规律及最大值依赖于内外层螺旋钢丝捻角，且外层螺旋钢丝捻角对其影响更为显著；同时，螺旋钢丝捻角变化对芯丝与内层螺旋钢丝接触引起的内部应力亦存在影响，但内层螺旋钢丝捻角对其影响更加显著。综上可见，为减小单股钢丝绳在扭转载荷下的钢丝内部应力，可适当降低螺旋钢丝捻角，特别是外层螺旋钢丝的捻角；为避免钢丝内部应力不均过大，单股钢丝绳内层和外层螺旋钢丝捻角等参数应合理匹配。

螺旋钢丝捻角对单股钢丝绳螺旋钢丝轴向应变演变的影响如图12所示，其中，轴向应变为正值和负值分别表示钢丝处于拉伸和压缩状态。从图12可知：内层和外层螺旋钢丝捻角变化对各自轴向应变有不同影响。外层螺旋钢丝捻角增大加剧了其自身的受压程度，而减小了内层螺旋钢丝的受拉程度。内层螺旋钢丝捻角增大加剧了自身的受拉程度，同时增大了外层螺旋钢丝的受压程度。因此，在保证钢丝绳工作性能要求时，适当降低内层和外层螺旋钢丝的捻角，在一定程度上能有效降低扭转载荷引起的轴向应变，平衡不同层钢丝间的轴向受力，提高钢丝绳的使用寿命。

图11 钢丝内部应力分布随接触深度的分布Fig.11 Distribution of stress in steel wires with respect to contact depth

图12 捻角对螺旋钢丝轴向应变的影响Fig.12 Influence of layer angles on axial strain of spiral steel wires

5 结论

1)本文建立的单股钢丝绳丝间多层耦合接触性能模型可实现具有多层结构的钢丝绳丝间线接触、点接触耦合接触性的准确求解。

2)单股钢丝绳丝间接触压力和接触变形均随着轴向扭转载荷增大而非线性增大，内层与外层螺旋钢丝间的接触变化最为明显，该区域在扭转载荷过大时可能最先发生应力屈服。

3)外层螺旋钢丝捻角增大将加剧单股钢丝绳所有层钢丝间的接触作用，而内层螺旋钢丝捻角增大可减小内外层螺旋钢丝间的接触变形，不同层钢丝间接触强度的均衡性由内层和外层螺旋钢丝捻角和扭转载荷等参数共同决定。

4)单股钢丝绳各丝间接触引起的最大钢丝应力位于接触界面下一定深度处，对于螺旋钢丝捻角较大的钢丝绳，其钢丝内部更容易发生局部应力屈服，且危险位置较小捻角钢丝绳更远离接触界面。

5)钢丝绳实际应用中，应综合考虑结构参数及载荷参数对整体性能的影响，采用较小的内、外层螺旋钢丝捻角能有效降低丝间摩擦磨损以及提高单股钢丝绳的抗扭强度、使用寿命。