响应面法优化复合酶法制备人参膳食纤维

李彤昕，唐金鑫，由高飞，于雷，毕云枫

吉林农业大学食品科学与工程学院（长春 130118）

人参属于五加科人参属多年生草本植物。在我国，人参历来被誉为“百草之王”，是“滋阴补生，扶正固本”之极品，含多种皂苷和多糖类成分。人参的肉质根为著名强壮滋补药，适用于抗疲劳、提高脑摄氧能力、调整血压、恢复心脏功能、神经衰弱及身体虚弱等症，也有祛痰、健胃、利尿、兴奋等功效。虽然我国是人参产量大国，但同时也是人参产业弱国。我国的人参加工利用率很低，产品加工中一般只提取皂苷等少量成分，而将人参渣丢弃。人参渣是人参活性成分提取过程中伴随产生的副产物，无副作用，而且其中还含有淀粉以及大量的膳食纤维等营养物质。

膳食纤维根据其溶解性分为水不溶性膳食纤维（IDF）和水溶性膳食纤维（SDF）。膳食纤维具有降低血糖水平、调节血脂水平、调整肠道菌群、防治便秘和结肠癌等功能特性。膳食纤维也可作为功能性食品基料添加到食品中，以提高食品的营养价值，从而推动功能性食品的发展[1-5]。纤维素酶是酶的一种，在分解纤维素时起生物催化作用，是可以将纤维素分解成寡糖或单糖的蛋白质；半纤维素酶是一种能使构成植物细胞膜的多糖类水解的酶类。纤维素酶在提高纤维素、半纤维素分解的同时，促进植物细胞壁的溶解，使植物细胞内溶物溶解出来，并能将不易消化的大分子多糖、蛋白质和脂类降解成小分子物质，有利于胃肠道的消化吸收[6-9]。此次试验以复合酶法制备人参渣膳食纤维，通过单因素试验和响应面试验优化提取工艺，以期提高原料的膳食纤维得率，对促进人参残渣的综合利用具有重要意义[10-13]。

1 材料与方法

1.1 材料与试剂

人参残渣（吉林宏久生物科技有限公司）；纤维素酶（活力50 U/mg，源叶生物科技有限公司）；半纤维素酶（活力20 000 U/g，源叶生物科技有限公司）；其他试剂均为分析纯。

1.2 仪器与设备

高速万能粉碎机（天津市泰斯特仪器有限公司）；DHG-9073BS-III电热恒温鼓风干燥箱（上海新苗医疗器械制造有限公司）；KYC-100B空气恒温摇床（上海新苗医疗器械制造有限公司）；H-2050R离心机（长沙湘仪离心机仪器有限公司）；LGJ-12冷冻干燥机（北京松源华兴科技发展有限公司）。

1.3 方法

1.3.1 人参渣膳食纤维的制备

干燥人参渣→粉碎，过筛→按料液比1∶15（g/mL）加水→调pH至4.8，加入纤维素酶→放入50 ℃摇床1 h（180 r/min）→取出放凉→调pH至4.8，加入半纤维素酶→放入50 ℃摇床1 h（180 r/min）→取出离心（4 000 r/min，20 min）→85 ℃烘干称重，得到的粉末即为不可溶性膳食纤维

1.3.2 单因素试验

准确称取一定量的人参渣，设计料液比（1∶15，1∶20，1∶25，1∶30和1∶35 g/mL）、纤维素酶和半纤维素酶的添加量（0.5%，1%，1.5%，2%和2.5%）、酶解时间（0.5，1，1.5，2和2.5 h）以及粒度（40，60，80，100和120目）的4个单因素试验，研究4个因素对人参不可溶膳食纤维提取率的影响，进而确定因素以及水平范围内响应面试验的设计。

1.3.3 单因素试验

在单因素试验结果的基础上，以IDF提取率为主要指标，选取料液比、加酶量、酶解时间和粒度为影响变量进行响应面试验。采用Design-Expert. V 8.0.6统计软件，设计四因素三水平二次回归方程，拟合各因素和总膳食纤维得率之间的函数关系[14]。试验因素水平见表1。

1.3.4 试验结果测定方法[15]

式中：m1为提取物中不可溶性膳食纤维质量，g；m2为提取物中的总膳食纤维质量，g。

2 结果与分析

2.1 单因素试验结果分析

2.1.1 料液比对IDF得率的影响

在不同料液比（1∶15，1∶20，1∶25，1∶30和1∶35 g/mL）、加酶量2%、酶解时间1 h、粒度40目的条件下，得到IDF并测定其含量，试验重复3次，研究不同料液比对人参渣IDF提取率的影响，结果如图1所示。随着料液比比例的增大，IDF提取率基本呈下降趋势。当料液比为1∶15（g/mL）时，IDF提取率达到峰值；当料液比为1∶20～1∶35（g/mL）时，IDF提取率整体呈下降趋势。这是由于酶浓度不变，随着底物浓度的减小，反应速率逐渐减小。综上可知，IDF的提取率在1∶15（g/mL）时达到最高，随后逐渐下降。

2.1.2 加酶量对IDF得率的影响

在不同加酶量（0.5%，1%，1.5%，2%和2.5%）、料液比1∶15（g/mL）、酶解时间1 h、粒度40目的条件下，得到IDF并测定其含量，试验重复3次，研究不同加酶量对人参渣IDF提取率的影响，结果如图2所示。随着加酶量的增加，IDF的提取率先升后降。当加酶量为0.5%～1.5%时，IDF提取率不变；当加酶量为1.5%～2%时，IDF提取率逐渐升高；当加酶量为2%～2.5%时，IDF提取率逐渐下降。这是由于纤维素酶和半纤维素酶在初始阶段对膳食纤维的含量有着限制作用，随着酶用量的增加，样品中纤维素与半纤维素的去除率增加，膳食纤维的提取率增高。但当加酶量达到2%以后，纤维素酶与半纤维素酶的用量对于样品已经达到饱和作用，所以IDF提取率不升反降[16]。综上可知，IDF的提取率在加酶量2%时达到最高，随后逐渐下降。

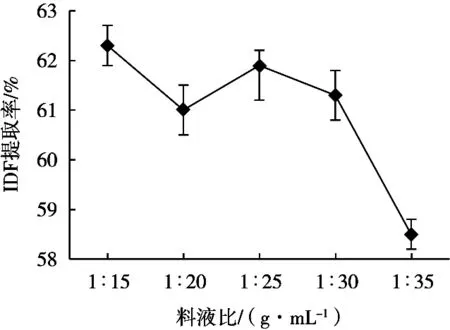
图1 料液比对IDF提取率的影响

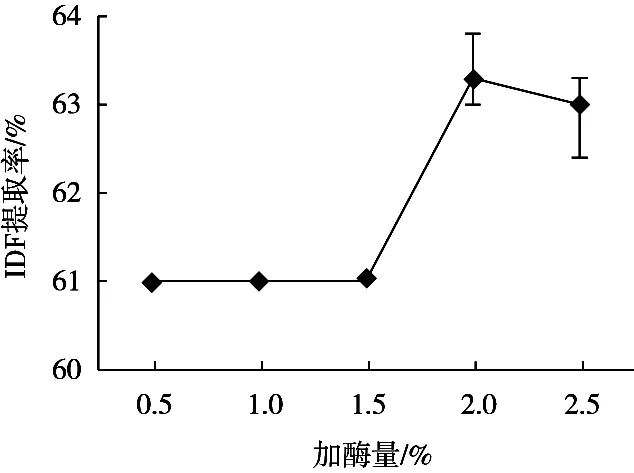
图2 加酶量对IDF提取率的影响

2.1.3 酶解时间对IDF得率的影响

在不同酶解时间（0.5，1，1.5，2和2.5 h）、料液比1∶15（g/mL）、加酶量2%、粒度40目的条件下，得到IDF并测定其含量，试验重复3次，研究不同酶解时间对人参渣IDF提取率的影响，结果如图3所示。随着酶解时间的增加，IDF的提取率呈下降趋势。当酶解时间为1 h时，IDF提取率达到峰值；当酶解时间超过1 h时，IDF提取率整体呈降低趋势。这是由于随着酶解时间的延长，纤维素酶与半纤维素酶充分酶解底物，导致部分膳食纤维聚合度降低，所以造成提取含量降低。综上可知，IDF的提取率在酶解时间1 h时达到最高，随后呈下降趋势。

2.1.4 粒度对IDF得率的影响

在不同粒度（40，60，80，100和120目）、料液比1∶15（g/mL）、加酶量2%、酶解时间1 h的条件下，得到IDF并测定其含量，试验重复3次，研究不同粒度对人参渣IDF提取率的影响，结果如图4所示。随着粒度的增加，IDF的提取率呈下降趋势。当粒度为40目时，IDF提取率达到峰值。因为膳食纤维的表面积大小和粒度直接相关，当人参渣的粒度为40目时，由于粒度降低，表面积较大，其更容易被酶解，IDF的提取率也较高；而在其由40目变为120目的过程中，IDF提取率显著降低，这可能是在粉碎过程中破坏了膳食纤维的部分连接结构，进而影响了IDF的提取率。综上可知，IDF的提取率在40目时达到最高，随后逐渐下降。

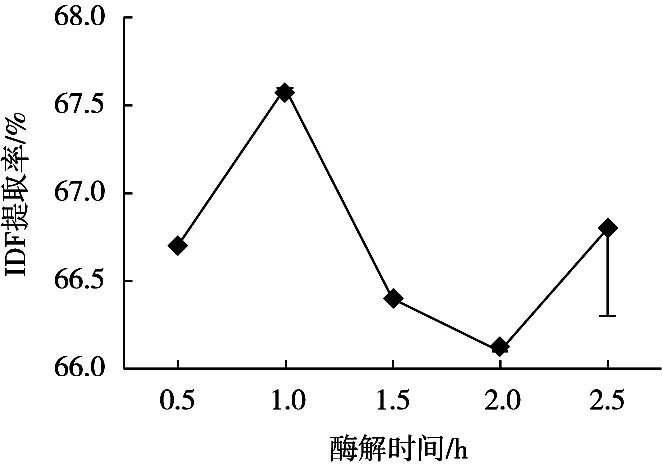
图3 酶解时间对IDF提取率的影响

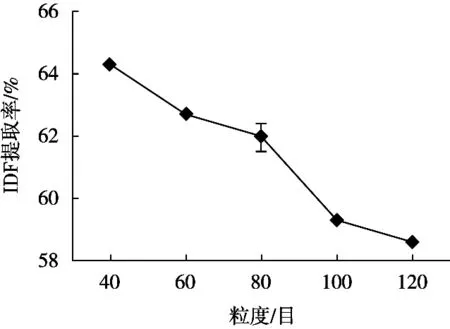
图4 粒度对IDF提取率的影响

2.2 响应面法优化试验结果分析

2.2.1 响应面试验优化设计及结果

采用Design-Expert. V 8.0.6统计软件设计，试验结果见表1，回归方差分析见表2。

采用Design-Expert. V 8.0.6统计软件，对表1中的试验数据进行二次多项式回归拟合，最终获得二次项回归方程：IDF提取率Y=+66.94+0.51A-0.72B+0.43C+1.30D-0.45AB-0.92AC+0.89AD-0.42BC+0.81BD+1.86CD-3.51A2-4.21B2-3.49C2-4.62D2。

回归方程中各变量对响应值影响的显著性用F检验来判定，概率p值越小，则响应变量的显著性就越高[17-19]。从表2可以看出，该模型效应显著（p＜0.05），不同处理间差异显著。因变量与所考察的自变量之间线性关系显著（R2=0.996 2），模型调整确定系数R2Adj=0.992 3，说明该模型可信度较高，拟合度较好。失拟项不显著（p＞0.05），说明此次试验所得二次回归方程能够很好地对响应值进行预测。从方差分析结果可以看出，各因素对IDF提取率的影响力大小的顺序为D＞B＞A＞C，即粒度＞加酶量＞料液比＞酶解时间。

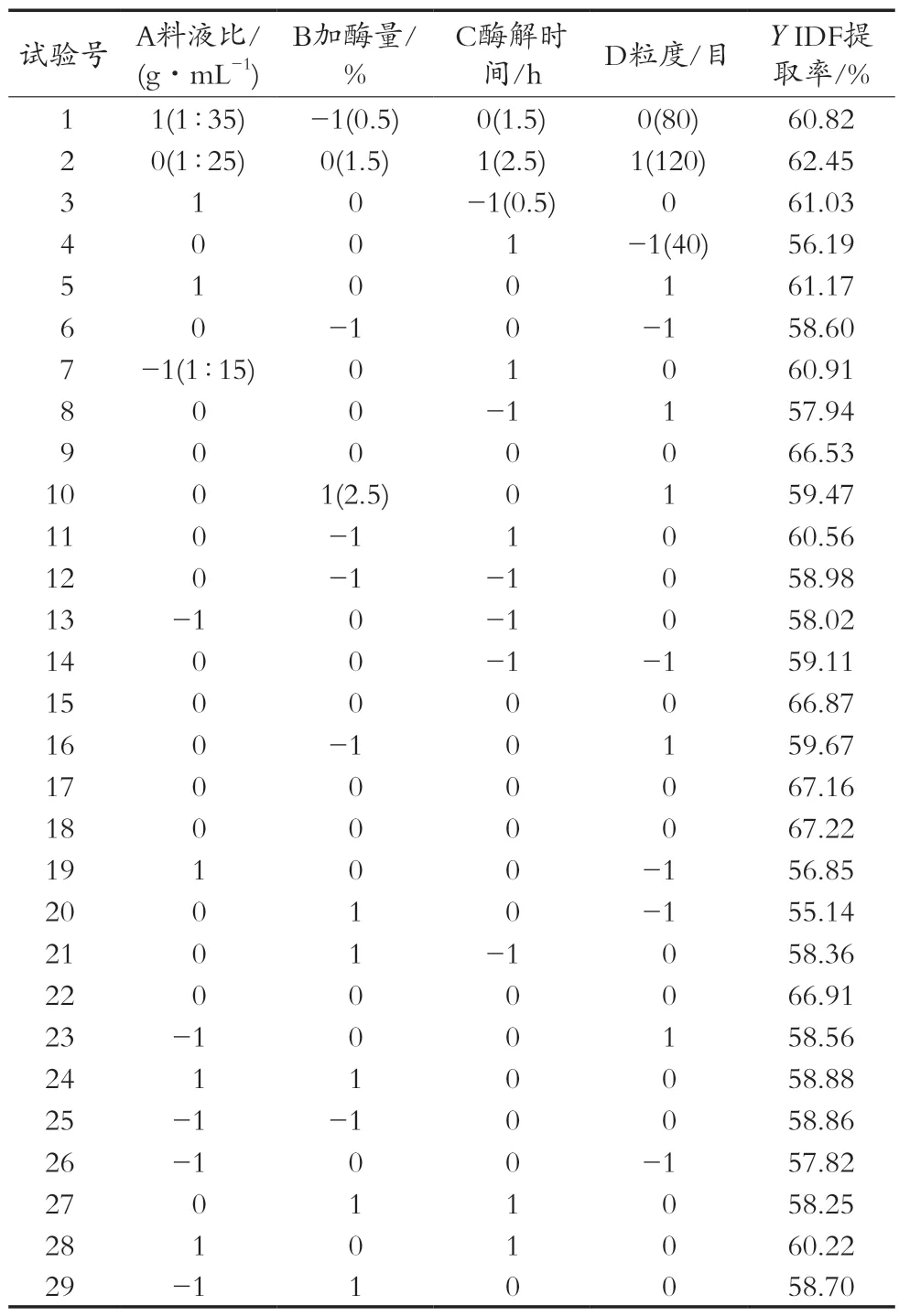
表1 Box-Behnken试验设计及结果

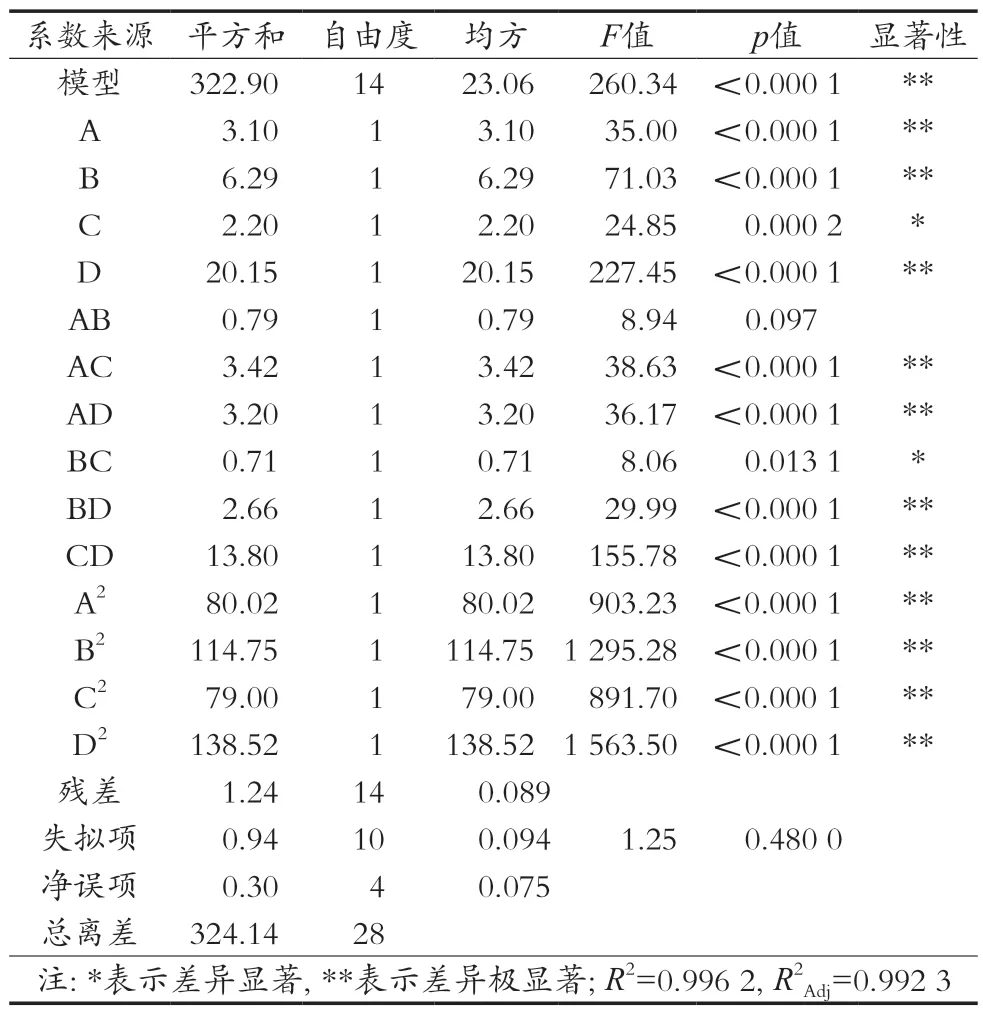
表2 响应面试验回归模型方差分析

2.2.2 响应面分析

利用Design-Expert. V 8.0.6软件进行四元二次回归拟合，得到回归方程的响应面等高线和曲面图。结果如图5所示。

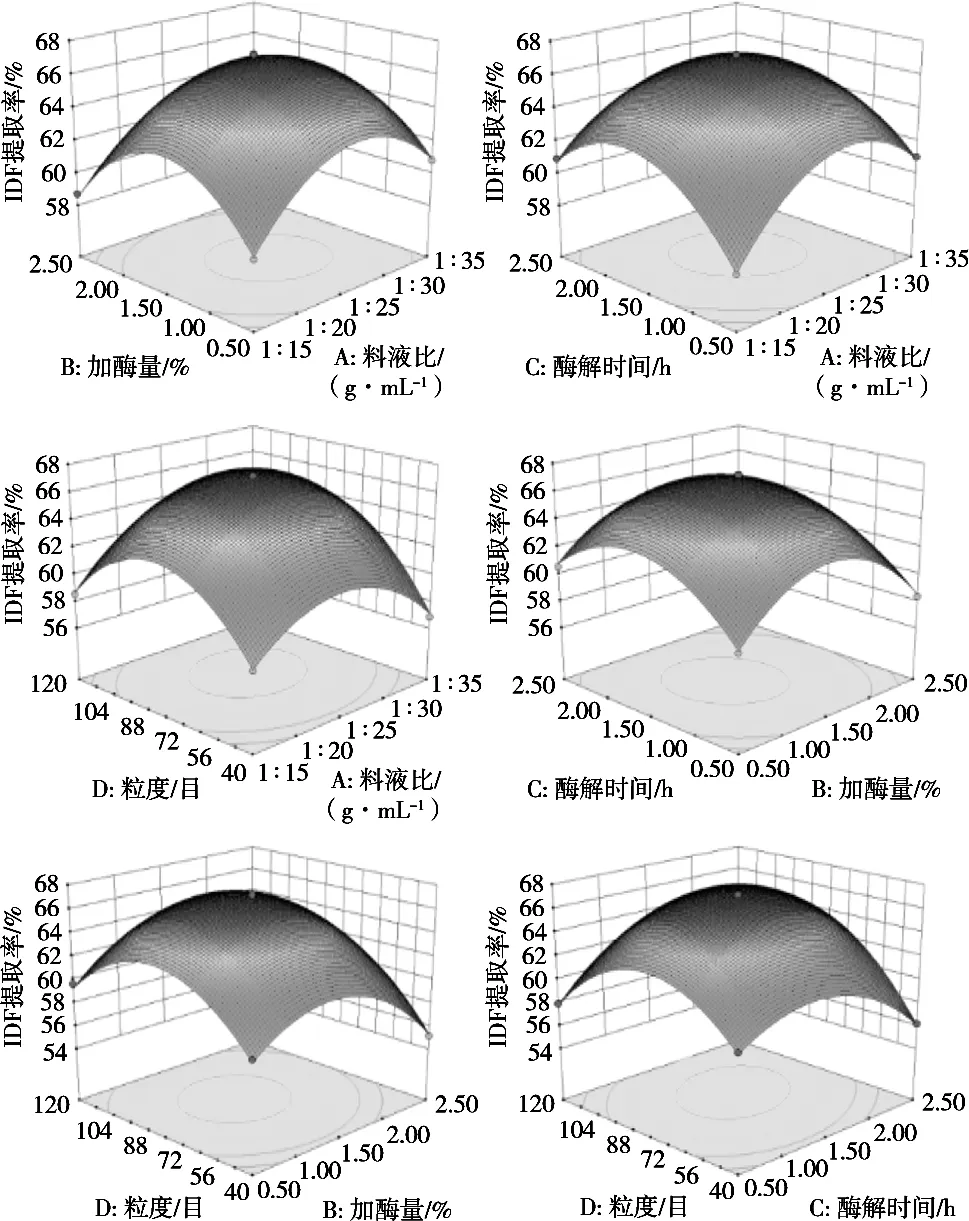
图5 两因素交互作用对提取率影响的响应面图

响应曲面反映了当料液比、加酶量、酶解时间、粒度4个因素的任意两个变量取零点水平时，其他2个因素的交互作用对不可溶性膳食纤维提取率的影响。曲面陡表明该因素对提取率的影响显著，曲面平缓表明该因素对提取率的影响不显著；等高线形状反映两因素交互作用的强弱，椭圆形表明交互作用强，圆形则表明交互作用弱；等高线密集表明对提取率影响较大，稀疏表明影响较小。

3 结论

经过响应面法优化，得到复合酶法提取人参渣不可溶性膳食纤维酶法的优化条件：料液比为1∶15（g/mL），加酶量2%，酶解时间1 h，粒度40目。在此条件下，不可溶性膳食纤维的提取率为67.57%。考虑到实际情况，在此条件下进行检验试验，重复3次，最后得到不可溶性膳食纤维提取率为67.15%，与模型理论预测值的偏差约为0.42%，与预测值较接近，说明该模型对试验拟合较好，即该响应面回归模型具有可行性，有一定的应用价值。