基于粒子群优化算法的碳纤维纱线用编织锭子结构参数的优化

杨晓东，孙志军，杜诚杰，叶 超

(东华大学 机械工程学院，上海 201620)

碳纤维作为一种新型高分子无机材料，因其耐腐蚀、耐高温、高强度、可编织和轻量化，常与编织工艺相结合制成碳纤维预制件[1]。随着复合材料的发展，通过现代工艺获得的碳纤维增强预成型件被广泛应用于航空航天、汽车制造等领域，由于碳纤维增强预成型件的广阔应用前景，许多专家学者对碳纤维编织进行了相关研究[2-3]。编织锭子作为碳纤维编织机中的重要组成部分，在编织过程中，编织锭子通过自身补偿碳纤维纱线长度，以确保碳纤维纱线张力稳定并满足加工要求。编织过程中碳纤维纱线张力波动对于碳纤维编织件品质影响非常大，碳纤维纱线会因纱线张力波动大，导致碳纤维单丝在变应力作用下发生断裂产生编织起毛问题。

为了降低编织锭子放纱阶段纱线张力波动，使碳纤维纱线在合适的编织张力下完成编织，需要对编织锭子的结构参数进行优化，但国内关于编织锭子方面的研究较少。王晗等[4]分析了影响纱线张力波动的因素，提出修改棘轮棘爪制动为摩擦制动以降低放纱阶段纱线张力波动；李荣林[5]为了提高钢丝编织胶管的品质，设计了钢丝编织摩擦锭子；扈昕瞳等[6]研究了不同放线速度对纱线张力波动的影响，证明了编织锭子快速放线可以缩小纱线张力波动范围；邢圆圆[7]、李宗迎[8]、贺辛亥等[9]都针对变截面三维编织方面进行了研究，并设计出了主动增减纱携纱器用于生产变截面三维编织预制件。 MA等[10]分析并建立了杠杆式编织锭子的纱线张力模型，同时研究了不同弹簧刚度条件下的纱线张力波动变化情况。ZHANG等[11]针对普通曲折法编织锭子进行了局部优化，并根据多刚体动力学理论建立了相应的纱线张力模型，所得仿真结果纱线张力波动优于普通曲折法编织锭子。

本文以自主设计的碳纤维纱线用编织锭子为基础，首先介绍花柱编织工艺和碳纤维纱线用编织锭子结构，并分阶段建立纱线张力模型；其次介绍粒子群优化算法原理，根据优化目标选择结构参数和优化目标函数并确定结构参数优化范围；最后确定粒子群优化算法参数，使用MatLab软件完成碳纤维纱线用编织锭子结构参数优化，并将优化结果与优化前和单补偿编织锭子实验结果比较，从而探求编织锭子结构参数优化对于纱线张力波动的影响。

1 碳纤维纱线用编织锭子纱线模型

1.1 花柱编织工艺与编织锭子结构

1.1.1 花柱编织工艺

在编织机底盘平面上有8个转度盘，每个转度盘有4个拨槽，编织锭子按照1F1E(2个编织锭子之间间隔1个空位)的方式安装在底盘平面上。在编织过程中，编织机驱动16个编织锭子随着转度盘沿着“8”字路径运动，根据编织锭子的运动方向一般分为2组，一组顺时针运动，一组逆时针运动，2组编织锭子释放的纱线重叠缠绕在芯模表面形成编织件。花柱编织工艺图见图1。

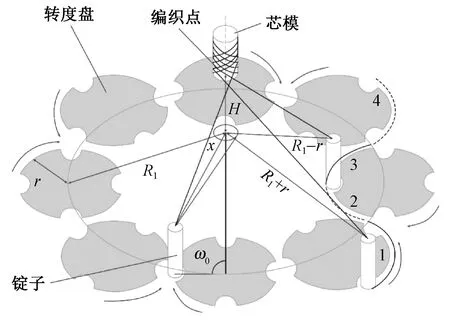
图1 花柱编织工艺图

在编织过程中，编织锭子出纱口与编织点之间纱线段长度随编织锭子运动不断变化，为准确求出编织锭子每个时刻出纱口纱线速度，以位置3作为编织锭子运动起点为例，根据编织机基本参数和转度盘角速度可得编织锭子出纱口与编织点之间纱线段长度变化表达式：

(1)

式中：R1为转度盘圆心到芯模圆心之间的水平距离，m；r为拨盘半径,m；r0为芯模半径,m；ω0为拨盘角速度,rad/s；t为时间,s；H为编织点与出纱口之间高度差,m；lc为出纱口到编织点之间纱线段长度,m。

编织锭子出纱口与编织点之间纱线段长度随时间的导数可通过式(2)求得出纱口与编织点之间纱线长度变化速度vc(m/s)。

(2)

由于编织锭子出纱口纱线速度与芯模移动速度有关，为了保证碳纤维纱线在芯模上以恒定的编织角缠绕，芯模的移动速度与转度盘的转动角速度之间存在一定关系，可根据芯模半径(r0)和碳纤维纱线宽度dt(m)求得纱线覆盖率100%条件下的编织角度β(rad)继而求得芯模移动速度v0(m/s)。

(3)

(4)

根据芯模移动速度v0，可以求出缠绕在芯模表面的碳纤维纱线运动速度vx(m/s)，综合出纱口到编织点之间纱线段长度变化速度vc，编织锭子出纱口纱线速度v(m/s)。出纱口纱线速度图如图2所示。可知，出纱口纱线速度的变化主要与编织锭子从最近端到最远端再到最近端这个机器循环的时间有关,即转度盘的转速有关，本文根据碳纤维编织机转度盘转速范围选择转度盘转速为π rad/s。

(5)

v=vc+vx

(6)

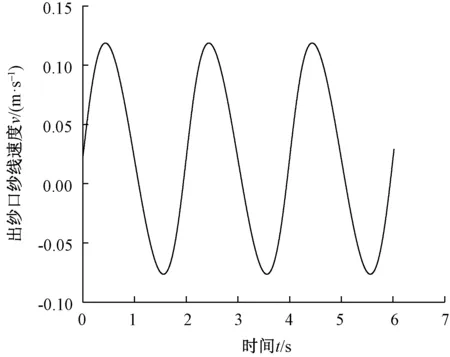
图2 出纱口纱线速度图

1.1.2 编织锭子结构

碳纤维纱线用编织锭子结构的出纱口、收放纱、纱线张力调控和纱线路径与普通杠杆式编织锭子不同，是对碳纤维材料做的针对性优化。编织锭子壳体上装有横轴1、2固定线坠，在线坠的另一端装有滑轮4，在横轴1下方有提杆与线坠一体。在横轴2的上方安装有弹簧3，利用弹力来限制横轴2的运动。当纱线被牵引出出纱口时，线坠顺时针旋转，弹簧1、2、3被压缩，滑轮1、2分别向右、向左移动，提杆同时顺时针旋转，最终提杆下端会与棘爪杆接触并将其抬起，实现放纱。碳纤维纱线用编织锭子三维结构轴测图见图3。

图3 碳纤维纱线用编织锭子三维结构轴测图

1.2 编织锭子中纱线长度计算

图4 碳纤维纱线路径图

为了分析碳纤维纱线用编织锭子中纱线张力变化，首先需根据编织锭子结构，计算编织锭子中碳纤维纱线长度变化。碳纤维纱线路径图见图4。可以看出，A点为碳纤维纱线退绕点；B1B2是缠绕在滑轮1上的碳纤维弧线段；C1C2是缠绕在滑轮2上的碳纤维弧线段；D1D2是缠绕在滑轮3上的碳纤维弧线段；E1E2是缠绕在滑轮4上的碳纤维弧线段；OS是纱线筒圆心；O1、O2、O3、O4分别是滑轮1、2、3、4的圆心；F为编织锭子出纱点。根据花柱编织工艺，在编织锭子运动过程中，出纱口与编织点之间纱线段与水平面之间的夹角随着编织锭子的位置变化而变化，从而导致纱线与出纱口之间的包角随之快速往复变化。为了改善该情况，碳纤维纱线用编织锭子中采用球铰式出纱口调节纱线与出纱口之间的包角使其变化较小，减少其对纱线张力波动的影响。为了准确求出纱线与球铰式出纱口之间的包角，需根据式(1)求出出纱口与编织点之间纱线段在水平面的投影距离lt，继而求出纱线与球铰式出纱口之间的包角φ(rad)。由于纱线与球铰式出纱口之间包角随时间变化不大，故假设球铰式出纱口处纱线段长度不变。为了简化模型计算，故将出纱点设为定点F。

(7)

(8)

在考虑纱线与碳纤维纱线用编织锭子路径中各构件之间包角变化的条件下，为了便于后续计算，将碳纤维纱线在退绕点A与出纱点F之间分为l1、l2和l3，以及纱线筒放纱量lf。当线坠处于初始状态时线坠旋转角度为θmin。当线坠旋转角度为θmid时，提杆与棘爪相接触。当线坠旋转角度为θmax时，棘爪杆离开棘轮，纱线筒开始放纱。当线坠旋转角度θmin<θ<θmax时，l1、l2和l3的长度发生变化。当线坠旋转角度θ>θmax时，纱线筒释放纱线并且l1、l2、l3和lf的长度发生变化。因此，碳纤维纱线编织锭子工作过程分为2个阶段，即纱线张力调节阶段和纱线筒放纱阶段，纱线张力调节阶段又分为并联弹簧作用和并联弹簧与棘爪杆共同作用阶段。

l1=lC1C2+lC2D1

(9)

l2=lAB1+lB1B2+lB2C1

(10)

l3=lD1D2+lE1E2+lD2E1+lE2F

(11)

(12)

式中：γ为纱线筒纱线缠绕角度,rad;α为纱线筒转动角度,rad；Rs为纱线筒半径,m。

根据编织锭子几何形状、滑轮1、2、3、4圆心坐标、纱线筒圆心坐标和出纱点坐标，运用勾股定理和2点之间距离公式得l1、l2、l3表达式为：

(13)

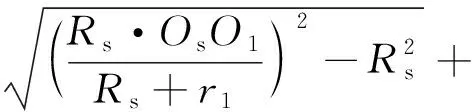
(15)

其中

(16)

式中：Oh为O2水平线与O3垂直线之间的交点；r1为滑轮半径,m;K为OhO2与OhO3的夹角，rad。

根据式(9)～(16)可求得l1、l2、l3和ls的变化。

(17)

1.3 编织锭子纱线张力模型

1.3.1 并联弹簧作用阶段

当纱线逐渐被牵引出出纱口时，线坠顺时针旋转，线坠角度θmin<θ<θmid，属于并联弹簧作用阶段，线坠受到滑轮4两端作用于线坠的纱线张力分力T33(N)、T44(N)，滑轮4重力G1(N)，线坠重力G0(N)和弹簧3弹簧力F3(N)作用。其中T33为滑轮右侧作用于线坠的纱线张力分力，T44为滑轮左侧作用于线坠的纱线张力分力。当线坠处于平衡状态时，T33与T44相等。并联弹簧作用阶段线坠受力分析图见图5。

(18)

F3=k3[Δs3+S3(tanθ-tanθmin)]

(19)

式中：l0为横轴1圆心与滑轮4圆心之间的距离,m；lr为横轴1圆心与线坠质心之间距离,m；S3为横轴1圆心与弹簧3之间的水平距离,m；k3为弹簧3的弹簧刚度，N/m；Δs3为弹簧3的预压缩长度,m；θ0为l0与lr之间的夹角,rad。

图5 并联弹簧作用阶段线坠受力分析图

根据式(9)～(17)采用微元法可得线坠转动的角速度和角加速度为：

(20)

(21)

由于横轴1处线坠旋转过程中会因摩擦产生摩擦力矩，故根据线坠构件受力分析将线坠所受的所有力分解到水平和垂直2个方向，同时根据T33和T44与水平方向的夹角可得式(22)和式(23)：

(22)

(23)

式中：Fhx为横轴1施加在线坠上的水平分力,N；Fhy为横轴1施加在线坠上的垂直分力,N；T44x为T44的水平分力,N；T44y为T44的垂直分力,N；T33x为T33的水平分力,N；T33y为T33的垂直分力,N；E0为滑轮4圆心O4的竖直线与滑轮4边缘的交点。

继而可根据式(18)～(23)建立线坠动力学方程：

(24)

式中：Mh为横轴1处摩擦力矩,N·m；J为线坠的转动惯量,kg·m2。

横轴1处摩擦力矩为

(25)

式中：r3为横轴1半径,m；μh为横轴1处摩擦因数。

线坠的转动惯量为

(26)

式中：ml为线坠的质量,kg。

由于滑轮4两端纱线张力还由弹簧1、2的弹簧力提供纱线张力分力，故需要对滑轮1、2进行受力分析。滑轮1、2处受力分析图如图6所示，在纱线张力调节阶段，纱线筒不放纱。根据式(27)、(28)可求得滑轮1下端纱线力Ttan1。

F1=k1[Δs1+S3tanθ-tanθmin]

(27)

(28)

式中：k1为弹簧1的弹簧刚度，N/m；Δs1为弹簧1的预压缩长度,m；F1为弹簧1施加的弹簧力,N。弹簧1、2受力分析图见图6。

图6 滑轮1、2和弹簧1、2受力分析图

(29)

F2=k2[Δs2+S3(tanθ-tanθmin)]

(30)

(31)

式中：k2为弹簧2的弹簧刚度,N/m；Δs2为弹簧2的预压缩长度,m；F2为弹簧2施加的弹簧力,N；Tz为纱线输出张力,N；Ts为纱线输入张力,N；B为纱线弯曲刚度，N/m；μ为纱线与构件之间的摩擦因数；φ为纱线与构件之间的包角,rad；Rq1为纱线在滑轮上的曲率半径,m-1；μh为纱线与滑轮之间的摩擦因数；kh为滑轮半径与纱线在滑轮上曲率半径的比值。

纱线绕过滑轮2和滑轮3后纱线张力变化可根据式(29)求得，结合线坠构件受力分析中的T33，由式(33)求得滑轮4右侧的纱线张力T3(N)，继而根据式(29)，由式(34)(35)分别求得滑轮4左侧纱线张力T4(N)和出纱口纱线张力T5(N)。

(35)

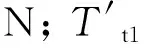
1.3.2 并联弹簧与棘爪杆共同作用阶段

当纱线继续被牵引出出纱口时，线坠继续顺时针旋转，提杆逐渐带动棘爪杆离开棘轮，此时θmid<θ<θmax，并联弹簧与棘爪杆共同作用阶段线坠受力分析图如图7所示，图中Fj为棘爪杆重力G2作用在提杆处的作用力，此时线坠构件在多力作用下处于平衡状态可得：

(36)

式中：lj为横轴1圆心与棘爪杆质心之间的距离,m；θj为提杆与线坠之间的夹角,rad；lt为横轴1圆心与提杆与棘爪杆的接触点之间的距离,m。

根据式(20)、(21)可得该阶段线坠旋转的角速度和角加速度，同时根据式(23)、(36)可得该阶段线坠构件的动力学方程(37)(38)。并联弹簧与棘爪杆共同作用阶段线坠受力分析图见图7。

(37)

图7 并联弹簧与棘爪杆共同作用阶段线坠受力分析图

(38)

继而根据式(27)～(35)求得T5。

1.3.3 纱线筒放纱阶段

随着纱线继续被牵引出出纱口，此时线坠角度θ>θmax，棘爪杆离开棘轮，纱线筒开始旋转放纱，随后纱线张力迅速下降，棘爪杆同时逆时针旋转，当线坠角度θ<θmax时棘爪杆迅速卡入下1个卡槽停止纱线筒旋转。根据并联弹簧与棘爪杆共同作用阶段中求出的T5，根据式(29)可依次求出T4、T3、T2、T1和纱线筒处纱线张力T0，根据对纱线筒进行受力分析可得纱线筒的动力学方程为：

(39)

(40)

式中：ms为纱线筒质量,kg；Is为纱线筒转动惯量,kg·m2；μs为纱线筒与轴摩擦因数；Gs为纱线筒重力,N；Rr为纱线筒内径,m；Rs为纱线筒的外径，m。

根据式(40)可求得纱线筒的角加速度，该阶段碳纤维纱线长度可根据微元法进行计算。

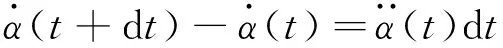
(41)

(42)

(43)

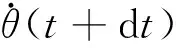
2 粒子群优化算法

粒子群优化算法是根据鸟类的飞行空间作为算法的解空间，根据种群中个体间的信息交流和共享不断更新种群中个体的飞行方向，朝着优化目标的方向飞行。由于粒子群优化算法中的粒子仅包含速度和位置信息，故需要通过对粒子本身速度和位置的不断更新来逐渐向全局最优解方向运动。粒子群优化算法通过跟踪解空间中个体和群体的历史最优解作为全局最优解的数据集[12-13]。

根据粒子群优化算法的基本原理，总结出算法所用到的参数如下：

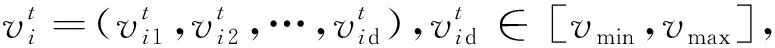
其中1≤i≤M，1≤d≤D，M为算法中种群粒子个数，D为优化目标函数中变量维数。

粒子在t+1时刻关于速度和位置更新公式如下：

(44)

(45)

式中：r1和r2为(0,1)之间随机数；c1和c2为因子。

为了能够更加准确地控制粒子开发和探索的比重，提升粒子群优化算法的全局寻优能力，一些学者在原有算法基础上通过在更新上增加惯性权重系数，原有粒子飞行速度更新公式转化为：

(46)

惯性权重系数ω用于调节种群中的粒子保持目前速度影响权重，根据实际经验ω的取值一般选取0.12～0.90为宜[14]。为了更加直观地了解粒子群优化算法的流程，粒子群优化算法流程见图8。

图8 粒子群优化算法流程

3 基于粒子群优化算法结构参数优化

3.1 初始结构参数仿真结果及分析

根据1.1中出纱口纱线速度表达式、1.2中碳纤维纱线用编织锭子中纱线长度变化的计算和1.3中建立的纱线张力模型，使用MatLab软件完成碳纤维纱线用编织锭子的纱线张力模型仿真，线坠角度变化图和出纱口纱线张力变化图分别如图9、10所示。

图9 线坠角度变化图

图10 出纱口纱线张力变化图

从图10可以看出，编织锭子在6 s后进入稳定工作阶段，出纱口纱线张力T5基本呈现周期性变化，因此详细分析6～8 s之间的碳纤维纱线张力仿真结果。在编织过程中碳纤维纱线用编织锭子放纱阶段纱线张力在3～4 N之间波动，波动范围较大且波动不够平稳。同时在6～8 s时间范围内，出纱口纱线张力T5会因出纱口与编织点之间纱线段长度变化而发生大张力变化即大波动。放纱阶段碳纤维纱线处于较大纱线张力阶段，由于放纱阶段纱线张力的大范围波动会导致碳纤维单丝在大变应力作用下发生断裂，从而严重影响编织产品质量和力学性能，因此有必要优化碳纤维纱线用编织锭子结构参数。同时还可以针对不同编织任务调整碳纤维纱线张力的波动范围，计算出合适的碳纤维纱线用编织锭子结构参数，从而提高编织产品合格率。

3.2 优化目标及优化目标函数

3.2.1 优化目标

碳纤维纱线用编织锭子通过线坠旋转、滑轮1、2运动和纱线筒放纱来调节碳纤维纱线张力。但碳纤维纱线张力波动会导致编织成品产生缺陷。为了获得更紧凑的编织产品，可以通过设定碳纤维纱线用编织锭子的优化目标，使用粒子群优化算法优化碳纤维纱线用编织锭子结构参数来实现。优化目标如下：①使碳纤维纱线张力在所需值附近波动；②降低放纱阶段的平均纱线张力波动；③降低编织过程中大张力变化。

3.2.2 优化目标函数

根据工厂实际编织情况选择适合碳纤维纱线编织的编织张力为5 N，结合优化目标和碳纤维纱线用编织锭子初始结构参数的仿真结果，选择优化的时间区间为6～8 s，可得优化目标函数的表达式如下：

(47)

3.3 结构参数选择及优化范围确定

根据对1.2和1.3中纱线长度计算和纱线张力模型分析可知，编织过程中碳纤维纱线张力主要受弹簧1、2、3的影响。弹簧1、2、3的工作时间主要由以下因素决定：θmin、θmid、θmax和l0。因此选择以下碳纤维纱线用编织锭子结构参数进行优化：弹簧1的预压缩量Δs1、弹簧2的预压缩量Δs2、弹簧3的预压缩量Δs3、弹簧1的弹簧刚度k1、弹簧2的弹簧刚度k2、弹簧3的弹簧刚度k3、线坠初始角度θmin、提杆与棘爪杆接触角度θmid、棘爪杆离开棘轮角度θmax、线坠长度l0。

根据对碳纤维纱线用编织锭子初始结构参数的仿真结果进行分析后发现，为了获得最优的编织锭子结构参数必须扩大和调整线坠的旋转角度范围。如图3所示，θmin、θmid和θmax的取值范围与碳纤维纱线用编织锭子的结构有关，根据碳纤维纱线用编织锭子的结构选取的最小值θmin和最大值θmax。线坠长度l0的取值范围与碳纤维纱线用编织锭子的结构尺寸和零部件之间的干涉有关，需要根据这2个因素进行参数范围的选取。k1、k2、k3、Δs1、Δs2和Δs3的值需要根据碳纤维纱线用编织锭子初始结构参数适当增加选择范围，综上所述碳纤维纱线用编织锭子初始结构参数如表1所示，碳纤维纱线用编织锭子的结构参数优化范围如表2所示。

表1 碳纤维纱线用编织锭子初始结构参数

表2 碳纤维纱线用编织锭子结构参数优化范围

3.4 编织锭子结构参数优化结果及分析

根据优化目标函数和编织锭子结构参数优化范围，完成粒子群优化算法中参数设置，粒子群优化算法优化前后出纱口纱线张力变化图见图11。

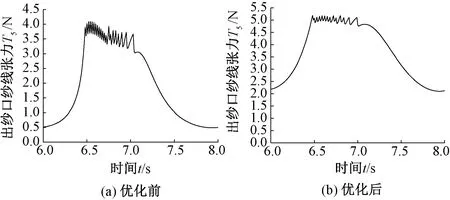
图11 粒子群优化算法优化前后出纱口纱线张力变化图

图11(a)所示为碳纤维纱线用编织锭子初始结构参数条件下在6～8 s时间范围内出纱口纱线张力T5随时间变化的曲线图，可以看出，在放纱阶段出纱口处纱线张力约在3.5 N附近波动，且波动幅度范围变化较大，波动不够平稳，不利于碳纤维纱线的编织。如图11(b)所示，为使用粒子群优化算法优化后的出纱口纱线张力T5随时间变化的曲线图，在放纱阶段出纱口纱线张力在5 N附近波动，相比于优化前放纱阶段纱线张力波动更加平稳，且波动范围变化不大，符合优化目标。粒子群优化算法优化前后的纱线张力比较如表3所示。

表3 粒子群优化算法优化前后的纱线张力比较

由表3可知，编织锭子结构参数优化后放纱阶段平均纱线张力波动率相比于优化前下降了5.05%，大波动幅值差相比于优化前下降了0.18 N。证明使用粒子群优化算法优化编织锭子结构参数对于降低纱线张力波动是有效果的。粒子群优化算法优化前后结构参数如表4所示。

表4 粒子群优化算法优化前后结构参数

为了验证碳纤维纱线用编织锭子结构参数优化后结果更适合碳纤维纱线编织，需要与其他类型编织锭子实验结果进行比较。文献[15]中通过电压传感器测量编织机编织过程中单补偿编织锭子实时纱线张力，根据文献[15]中单补偿编织锭子纱线张力实测数据和图11中数据分析可知，碳纤维纱线用编织锭子放纱阶段平均纱线张力波动率相比于单补偿编织锭子下降了18.13%，证明碳纤维纱线用编织锭子放纱阶段平均纱线张力波动更小，更适合碳纤维纱线的编织。

4 结 论

本文以自主设计的碳纤维纱线用编织锭子为基础，结合花柱编织工艺和编织锭子中纱线长度计算表达式，分阶段建立了碳纤维纱线用编织锭子纱线张力模型，得到了结构参数与碳纤维纱线张力之间的关系。然后通过MatLab软件使用粒子群优化算法完成碳纤维纱线用编织锭子的结构参数优化，并对优化结果进行比较和分析，得出如下结论：

①通过分析碳纤维纱线用编织锭子中纱线长度变化，结合碳纤维纱线用编织锭子中各构件受力分析，建立的纱线张力模型，所得仿真结果能够更加直观地看出编织过程中纱线张力的变化过程。

②通过调节弹簧刚度、弹簧预载荷长度、线坠摆动角度和线坠长度可以使放纱阶段纱线张力保持在所需值附近较小范围内波动。

③使用粒子群优化算法优化碳纤维纱线用编织锭子结构参数后，放纱阶段平均纱线张力波动率相比于优化前有明显下降，相比于单补偿编织锭子实验数据下降了18.13%，证明使用粒子群优化算法优化编织锭子结构参数是有效果且具备可行性的。