基于DEM 与Logistic 函数的灌区渠系工作制度模拟
——以周桥灌区为例
刘 永,缴锡云,2,3*,程明瀚,李 江
(1.河海大学 农业工程学院,南京 210098;2.水文水资源与水利工程国家重点实验室, 南京210098;3.河海大学 水安全与水科学协同创新中心,南京 210098)
0 引 言
【研究意义】农业生产是我国的用水主体,灌溉是农业生产的前提。根据《第一次全国水利普查公报》,全国大中型灌区的灌溉面积占总灌溉面积的50.20%[1],因此在水资源紧缺的大背景下,大中型灌区的水资源高效利用具有重要的意义。【研究进展】目前,对于大中型灌区来说,渠道级别多、数量大,渠道输水效率、干支渠水位稳定性、末级渠道水位高低等对于灌区的高效、稳定运行具有重要的影响[2-4],因此渠系调度是大中型灌区高效运行与节水的重要环节。渠系工作制度优化的目标主要分为2 大类[5]:一是以灌区某次配水增产效益最大为目的优化渠道配水。前人基于人工鱼群算法[6]、“Generalized Wolfe”算法[7]、作物水分生产函数[8]等模型对灌区渠系配水进行模拟优化,实现对灌区灌溉效益的优化。二是以输水损失量最小为目标对渠道进行优化配水;宋静茹等[9]、马孝义等[10]基于遗传算法,以轮灌期间所有配水时段的渠道输水损失最小为目标建立了渠道优化配水模型,解决了渠道引水流量不稳定情况下的渠系优化配水决策问题。Suryavanshi 等[11]建立0-1 线性规划配水模型,对渠道配水及轮灌方式进行优化,减少了灌区渠道输水损失及工程成本。宋松柏等[12]、吕宏兴等[13]提出渠道配水均一化方法,应用遗传算法对配水渠道流量优化求解,实现同级渠道的同时关闭,解决了配水渠道闸门多次调节的问题。
【切入点】对于平原灌区,自流灌溉面积也是衡量灌区渠系工作制度优劣的一个重要指标,不同渠系工作制度会产生不同的渠道水位,进而对灌区自流灌溉面积产生巨大影响。然而,上述渠系工作制度优化研究主要是以灌区效益最大化、输水损失小为目标函数,没有将自流灌溉面积作为优化目标考虑进去。【拟解决的关键问题】周桥灌区为洪泽湖东岸的大型平原自流灌区,灌溉配水制约因素较多。灌区自流灌溉面积受水位影响较大,往往由于10~30 cm 的水头差,导致整个灌区中大面积农田无法自流灌溉。因此,本文以周桥灌区为例,以ASTER GDEM 数据[14-15]及实测高程为基础,结合Logistic 函数建立渠首闸后水位与灌区自流灌溉面积的关系模型,模拟不同渠系工作制度下周桥灌区的自流灌溉情况,确定最优渠系工作制度,以提高灌区自流灌溉面积,为周桥灌区灌溉决策提供参考。
1 材料与方法
1.1 研究区概况
周桥灌区位于江苏省淮安市洪泽区中北部,东经118°47′40″—119°07′35″,北纬33°11′01″—33°23′25″,西靠洪泽湖,南以草泽河为界、与淮安洪金灌区毗邻,东连白马湖,北连苏北灌溉总渠。跨高良涧、黄集、朱坝、岔河4 镇(街道)全部及东双沟镇部分区域,耕地面积2.433 万hm2,约占全区耕地面积的62%,设计灌溉面积2.133 万hm2。周桥灌区主要通过渠首周桥洞引用洪泽湖水及黄集洞、薛桥洞从苏北灌溉总渠补水进行灌溉。灌区现有总干渠、砚临干渠、浔南干渠、浔北干渠等4 条干渠,总长48.2 km;流量1 m3/s以上的渠道、灌排结合渠道96 条,总长302 km。周桥灌区渠系分布见图1。

图1 周桥灌区渠系分布图 Fig.1 Distribution of channel system in Zhouqiao irrigation district
1.2 研究方法
1.2.1 数字高程模型(DEM)构建
兹通过实测高程数据对ASTER GDEM 数据进行拟合,构建周桥灌区DEM。ASTER GDEM 数据为NASA 于2009 年发布的覆盖全球98%以上陆地DEM,是目前使用广泛的数字高程模型,具有覆盖度广、精度高的特点[16-17],DEM 是模拟地表高程变化特征的主要方式,灌区田面高程分析建立在该模型的基础上。结合周桥灌区实测高程点数据,图形法建立周桥灌区DEM 可分为2 步:第一步,对灌区内多个离散点的高程数据进行空间差值从而构成不规则网络(TIN)模型;第二步,在不规则网络模型的基础上生成规则网格(Grid)模型。
1.2.2 自灌率模型构建
本文将水源水位一定条件下的灌区自流灌溉面积占灌溉总面积的百分比定义为自灌率[18]。干渠渠首水位扣除沿程水头损失,以及沿程各种渠系建筑物的局部水头损失,推算出农渠的控制点水位(闸后水位),根据控制点水位结合DEM 进行空间分析,提取控制单元内各点高程得出相邻等高线之间栅格数目,计算出各渠道控制范围内对应的耕地面积,即自流灌溉面积。本文以DEM 为基础结合Logistic 函数,得到周桥灌区不同地块的自灌率模型。
1.2.3 渠系工作制度模拟
周桥灌区的渠系调度方式不同于常规灌区以某一级渠道作为轮灌组,而是通过节制闸划分轮灌组,本文根据灌区内设立的22 个节制闸将灌区划分为16个灌溉单元(图1),每个灌溉单元内实行续灌。根据灌区灌溉单元,选择分条轮灌、分段轮灌、分片轮灌以及现行轮灌4 种渠系工作制度,通过自灌率模型模拟不同渠系工作制度下灌区自流灌溉情况,寻求周桥灌区最优渠系工作制度。
2 结果与分析
2.1 DEM 率定与验证
根据统计学理论,采用相关系数R、平均偏差MBE 等2个指标对周桥灌区ASTER GDEM 数据进行评估,通过最小二乘法[19]用实测数据率定ASTER GDEM 数据,计算式为:
式中:H0为ASTER GDEM 数据(m);H1为实测数据(m);a、b 为回归系数。
据统计,周桥灌区实测高程在5.4~12.8 m 之间,ASTER GDEM 数据在4.0~12.7 m 之间,二者拟合关系见图2。经计算,ASTER GDEM 数据与实测数据的相关系数R 达到0.96,MBE 为0.27 m,2 组数据偏差较小,相关性高。本次验证的样本数据共349 个,其中有327 个数据的ASTER GDEM 高程值小于实测值,表明周桥灌区ASTER GDEM 数据整体偏小,与郭笑怡等[20]研究结果相似,但周桥灌区 ASTER GDEM 数据与实测值线性相关系数R 达到0.96,说明二者之间存在紧密的相关关系。通过最小二乘法构建ASTER GDEM 与实测值的线性关系,计算式为:

根据此关系式可得到率定后的周桥灌区数字高程模型,其与周桥灌区实际高程基本吻合,能够反映出不同地块的高程情况。因此,DEM 可用于模拟周桥灌区自流灌溉面积与渠首闸后水位的变化关系。
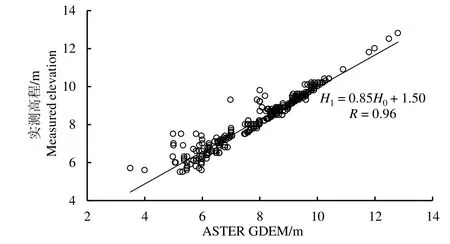
图2 ASTER GDEM 与实测数据线性回归 Fig.2 Linear regression of Aster GDEM and measured data
2.2 各灌溉单元自灌率模型
以地块#1 为例计算该灌溉单元的自灌率,自灌率与渠首闸后水位关系见图3。自灌率随闸后水位的上升呈先慢后快又变慢的趋势,符合Logistic 曲线分布,Logistic 曲线的数学模型[21]如下:
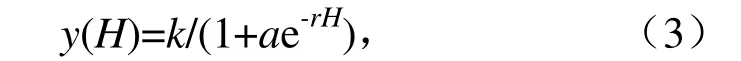
式中:y(H)为自灌率(%);H 为闸后水位(m);a、r、k 为根据实际地形信息确定的参数(k>0、r>0、a∈R)。

图3 地块#1 自灌率与闸后水位关系曲线 Fig. 3 Relation curve between self-irrigation rate and water level behind sluice in plot 1
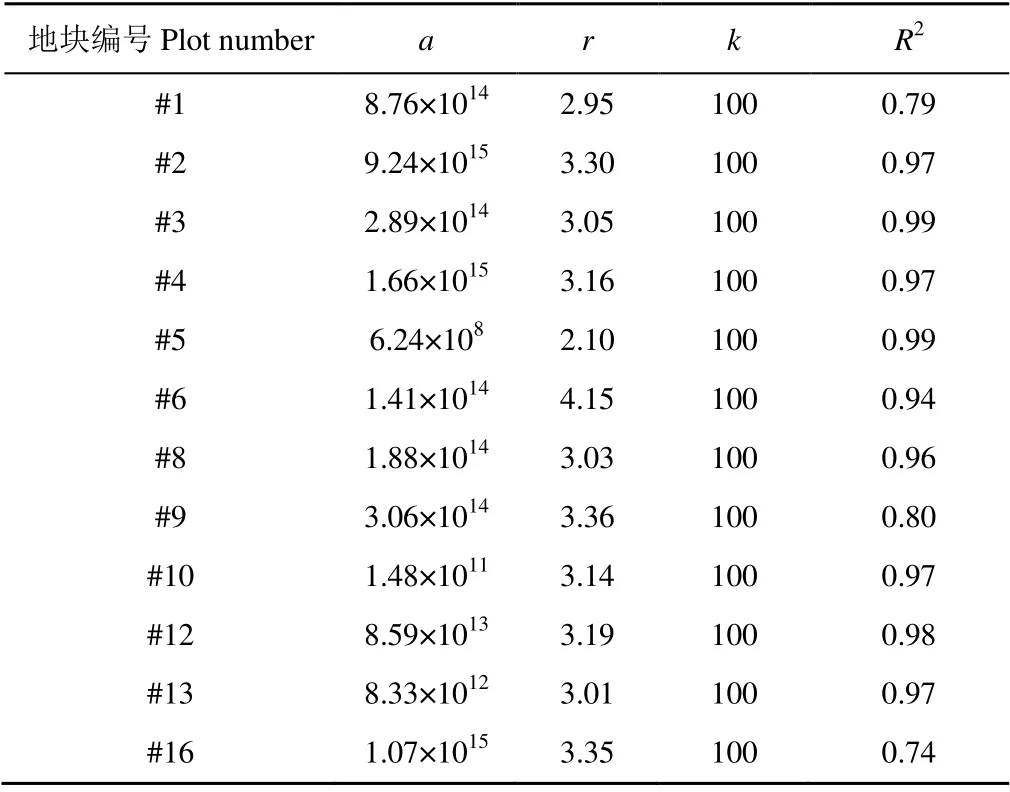
表1 自灌率模型相关参数 Table 1 Relevant parameters of self-irrigation rate model
表1为各地块的自灌率模型相关参数。由表1可知,各地块自灌率与闸后水位的决定系数R2均在0.74 以上,拟合度较高。因此,利用Logistic 曲线建立自灌率模型可模拟灌区不同渠系工作制度下自流灌溉情况。
2.3 渠系工作制度模拟及比较
洪泽湖水位变化情况:水稻灌溉季节最高水位13.59 m,最低水位12.01 m,平均水位为12.80 m;本文以洪泽湖的平均水位12.80 m 为例,灌水周期为6~8 d,起始时间约为7 月21 日—8 月10 日,该时间段周桥灌区用水限额为0.583 亿m3,流量上限为30 m3/s。设计分条轮灌、分片轮灌以及分段轮灌等3种渠系工作制度,代入模型进行自灌率模拟并与现行轮灌进行对比。分条轮灌以支渠或分干渠控制区域为划分依据,即以每条分干渠/支渠为一个轮灌组将灌区划分为6 个轮灌组,见图4(a);分片轮灌按分干渠或支渠将灌区划分为5 个集中片区,每个片区作为1 个轮灌组,见图4(b);分段轮灌是按分干渠/支渠将灌区分为3 段轮灌,每段1 个轮灌组,见图4(c);现行轮灌是周桥灌区现行轮灌方式,灌区划分为5 个片区,每个片区作为1 个轮灌组,见图4(d)。
不同渠系工作制度的自灌率模拟结果见表2。基于自流灌溉面积并结合输水损失、渠系水利用系数等辅助指标进行对比,确定最优渠系工作制度。其中渠系输水损失、渠系水利用系数可表示为:

式中:Vs为该渠道毛配水流量(m3/s);t1、t0分别为灌水结束时间和灌水开始时间(h);ηs为支渠及以上渠系水利用系数(无量纲);q支净为支渠的净流量(m3/s);q干毛为支渠的净流量(m3/s)。
由表2 可知,4 种渠系工作制度的自流灌溉面积占比均达到96%以上。对比4 种渠系工作制度,现行轮灌的自流灌溉面积占比为96.59%,分片轮灌的自流灌溉面积和自灌率最大,为20.67 万hm2和97.11%,分段轮灌和分条轮灌自流灌溉面积基本相同,基于自灌率最大的目标,4 种渠系工作制度以分片轮灌为最优。对比渠道输水损失,相对现行轮灌,分片轮灌和分段轮灌的渠道输水损失分别减少了 45.37%、13.56%,而分条轮灌的输水损失增加了3.34%。对比渠系水利用系数,分条轮灌和现行轮灌渠系水利用系数差别不大,均在0.65 左右,分段轮灌、分片轮灌的渠系水利用系数分别为0.69、0.78,较现行轮灌分别提高了4.55%、18.18%,均优于现行轮灌,其中分片轮灌最优,分片轮灌输水损失小且提高了灌区的渠系输水效率。

图4 4 种渠系工作制度概化图 Fig.4 Generalized diagram of channel work system

表2 渠系工作制度模拟结果 Table 2 Simulation results of channel work system
3 讨 论
合理的渠系工作制度对自流灌区实现自流灌溉面积最大化十分重要。本文利用DEM 和Logistic 函数建立周桥灌区自灌率模型,将自流灌区自灌率与水源水位建立数学关系,为模拟灌区渠系工作制度提供了重要方法。
数字高程模型是实现灌区自流灌溉面积定量估算的有效手段。ASTER GDEM 数据在周桥灌区整体偏小,其值与实测数据相关系数达到0.96,呈极显著相关。夏涛等[22]、惠凤鸣等[23]研究也表明,ASTER GDEM 数据与实际高程存在一定误差,但是ASTER GDEM 数据与实测数据相关性高,故利用ASTER 数据提取DEM 经率定后可用于模拟不同闸后水位的灌区自流灌溉情况。相对传统单点测量的形式,无人机测量能提供面上的数据,且无人机的高程测量精度最高可达到±5 cm 的水平,另外无人机的特性也保证了其空间分辨率较卫星数据有巨大的提升。因此为了提高自灌率模型的精准度,无人机将会是下一步灌区灌溉合理化的研究方向。
通过周桥灌区数字高程模型,结合Logistic 函数对闸后水位和自灌率的关系进行拟合,建立周桥灌区自灌率模型,发现各地块闸后水位与自灌率的决定系数R2均在0.74 以上,拟合度高,该模型可用于模拟自流灌区不同渠系工作制度的自流灌溉情况,这与宋静茹等[18]研究结果一致。将分条轮灌、分段轮灌、分片轮灌以及现行轮灌等4 种渠系工作制度分别代入该模型进行模拟,确定不同工况下周桥灌区的自灌率,并结合输水损失和渠系水利用系数等参数进行比选,其中分条轮灌和现行轮灌的3 个指标之间无显著差异,分段轮灌的输水损失以及渠系水利用系数优于现行轮灌,但其自流灌溉面积较现行轮灌降低1.46%,而分片轮灌的自流灌溉面积占比达到97.11%,输水损失为172.74 万m3,渠系水利用系数为0.78,较现行轮灌工作制度的自灌率和渠系水利用系数提高了5.84%、18.18%,输水损失降低了45.37%,提高了灌区自流灌溉面积且输水损失小、渠系水利用系数高,为最优的灌区渠系工作制度。
4 结 论
1)ASTER GDEM 数据经实测值率定后,与周桥灌区的实际高程基本吻合,可建立周桥灌区DEM。
2)不同地块自灌率模型拟合度较高,决定系数均达到0.74 以上,可用自灌率模型模拟周桥灌区不同渠系工作制度自流灌溉情况。
3)将4 种渠系工作制度分别带入该模型进行模拟,4 种渠系工作制度中分片轮灌为最优渠系工作方式,可将分片轮灌结合自灌率模型应用到周桥灌区灌溉系统中,提高灌区的灌溉水平。

