基于多目标粒子群算法的渠系优化配水研究

李彤姝，黄 睿，孙志鹏，郭珊珊，易 康，韩 宇*，陈 建

（1.中国农业大学 水利与土木工程学院，北京 100083；2.中国农业大学 信息与电气工程学院，北京 100083；3.中国农业大学 工学院，北京 100083）

0 引 言

【研究意义】我国是农业大国，2018 年《全国水利发展统计公报》显示，我国现有农田有效灌溉面积6.8×107hm2，农业用水占用水总量的61.4%[1]，保障农业用水是保证国民经济的基础[2]。农业用水虽然占比大，但水土资源的严重紧缺与不合理利用问题一直存在。并且由于灌溉时仍使用经验性灌水方式，导致渠系水量调度不合理，水量浪费严重，加上恶劣的自然条件等因素使得水土资源匹配处于严重错位状态，农业生产及耕地的开发受到水资源条件的严重限制[3]，因此采用农业节水措施是必要的[4]。节水首先要做到合理用水，农业灌溉用水主要来自渠系供水[5-6]，科学合理的渠系配水过程可以大大提高灌溉水的利用率，减少无效弃水。渠系配水作为灌溉调度管理的基础组成部分，对缓解水资源压力和农业水资源高效利用有着重要意义。

【研究进展】研究人员对渠系优化配水方法开展了大量研究。Suryavanshi 等[7]通过人工规划方法，最早假定上级渠系配水渠道是由一组等流量流管组成，其流量等于下级渠道流量之和，以减少渠道工程投资为目标，建立了线性优化模型。吕宏兴等[8]首次提出了引水时间均一化处理各轮灌组的方法，并在支渠以下各级配水渠道得到0-1 线性整数规划模型，使各下级进水闸在同一时间关闭。何春燕等[9]以农业效益和灌溉管理部门的经济收入之和最高为目标，建立了基于作物水分生产函数的渠系优化配水模型。但这种配水方法与当地种植的作物种类有很大关系，当作物种类不单一时，则需要研究每一种作物的水分生产函数。

智能算法的兴起为求解渠系优化配水模型提供了新思路。Wardlaw 等[10]证明了遗传算法能够快速求解模型，并具有求解精度高、全局性和鲁棒性，相比于线性规划方法，在求解下级渠道优化配水问题上具有良好的性能。汤瑞凉等[11]采用熵权系数法，综合考虑农业可持续发展的经济、社会和生态效益，提出了针对灌区水资源优化配置的多准则综合评价的熵权系数优化模型。张智韬等[12]将遥感技术和地理信息系统进行有机的结合，利用蚁群算法在GIS 系统中对灌区水费收入最高为目标的配水模型进行求解，获得各斗渠的最优配水量。赵文举等[13]引入动态罚函数处理约束条件，并提出基于模拟退火遗传算法求解渠系优化配水问题。Sun 等[14]将遗传算法和回溯搜索算法相结合，提出了利用遗传回溯算法（GBSA）对渠系优化配水模型进行求解，发现可以更好地缩短配水时间以及优化剩余水量。刘照[15]选择全灌区渠道渗漏损失水量与各轮灌组之间引水持续时间差异值同时最小作为优化目标，建立了基于粒子群算法的多级渠系优化配水编组模型，并且将WebGIS 与渠系优化配水系统结合了起来，提供了一个多功能的决策管理操作平台。张国华等[16]考虑了下级渠道流量不等和上级渠道断面变化的精细化条件，通过构建合理的适应度函数和对约束条件的高效处理，应用自由搜索算法对渠系优化配水模型进行了求解，进一步拓宽了模型的应用范围。

优化算法如遗传算法（VEGA）、回溯法（BSA）、粒子群算法（PSO）等在解决渠道优化配水的问题上已经得到了广泛的研究，既可以给定约束，又可以根据所需目标进行优化，能够在合理的时间限制内逼近优化问题的较好可行解[17]。【切入点】纵观前人的研究，在利用优化算法进行渠道优化配水时大多将目标函数定为输水历时最短，目标较单一。本文为使模型能够更加符合实际的渠系运行情况，考虑以水流过渡平稳和渠系水渗漏量最小作为优化双目标，利用多目标粒子群算法建立黑河流域西浚灌区西洞干渠及其下级渠道配水优化调度模型。【拟解决的关键问题】通过求解模型，最终获得各支渠的流量、灌水时间分布和基于水流平稳的条件下的渠系最小渗漏量，同时与向量评估遗传算法及回溯搜索算法2 种算法进行对比，分析多目标粒子群算法的合理性和实用性，为黑河流域生态灌区建设提供科学依据。

1 渠系优化配水模型及算法

1.1 多目标渠系优化配水模型

为使渠系优化配水模型更符合实际渠道输水情况, 本研究以水流过渡平稳、渠道渗漏量达到最小为优化目标，以配水时间作为决策变量建立模型。

1）目标函数

渠系渗漏计算采用经验公式，对于渠道最小流量与加大流量的约束系数采用经验系数，参照《农田水利学》[18]。

1.2 多目标粒子群优化算法（MOPSO）

粒子群算法[19]（PSO）基本思想来源于鸟群的随机捕食行为，通过鸟群自身经验和种群之间的交流调整自己的搜寻路径，来找到食物最多的最优地点。粒子群算法是从随机解出发，通过迭代寻找最优解，但比遗传算法规则更为简单，通过追随当前搜索到的最优值来寻找全局最优。因此粒子群算法直接用粒子经初始约束的位置来表示自变量，设初始粒子个数为N，其中每个粒子的位置x都由自变量个数和取值范围决定，变化速度同时也相应由其个数N 和速度v 限制决定，位置与速度的表式分别如下：

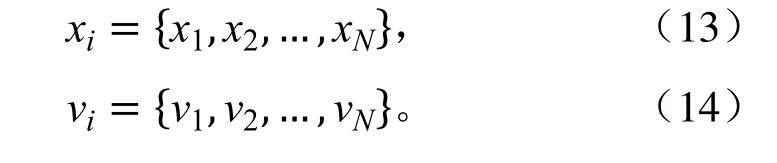
每一次迭代过程在允许的搜索空间范围内，关键点为每个粒子位置和速度的更新，而其中位置的更新取决于该粒子自身速度的更新，综合考虑惯性权重、个体学习因子、群体学习因子和基于历史位置与速度基础上来综合进行下一过程中位置与速度的确定，其中单一迭代的具体过程如下：

MOPSO 是基于原始粒子群算法（PSO）提出来的，它将原来只能用在单目标上求解的粒子群研发应用于多目标优化问题的求解，MOPSO 能在实际相应约束条件下，于更短时间内在全局范围中找到多目标优化问题的非劣解。

2 研究区概况

本文以黑河中游流域张掖市的西浚灌区作为研究区域，选取西洞干渠进行优化对象。西浚灌区总面积6.586 万hm2，年无霜期约为145 d，年均日照时间3 058 h，年均气温约7 ℃；平均降水量125 mm，平均蒸发量为2 047.9 mm。西洞干渠渠系分布见图1，下设西洞支渠、毛家湾支渠及9 个直属斗渠，渠道设计参数见表1。干渠控制灌溉区域现状渠系水利用系数0.556，灌溉水利用系数0.484。采用2007 年甘州区配水计划中夏灌三轮的灌水数据，轮灌周期为25 d，综合灌水定额为1 200 m3/hm2，预计来水量280.5 万m3，配水计划总量150 万m3，干渠的平均输水流量1.298 m3/s。渠系分布示意图和渠道设计参数如下：

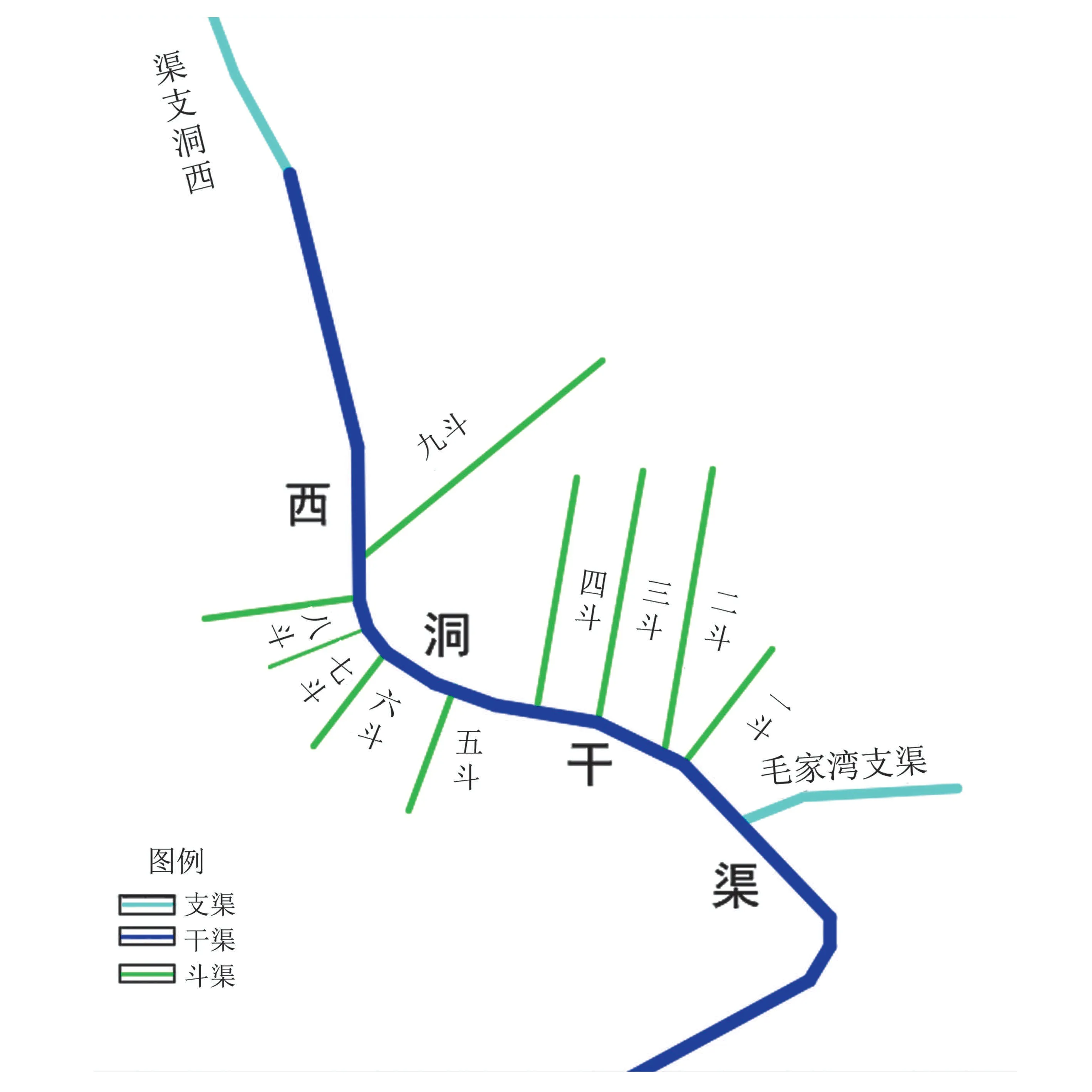
图1 西洞渠系布置图 Fig.1 Graph of the Xidong main canal and its branch canals

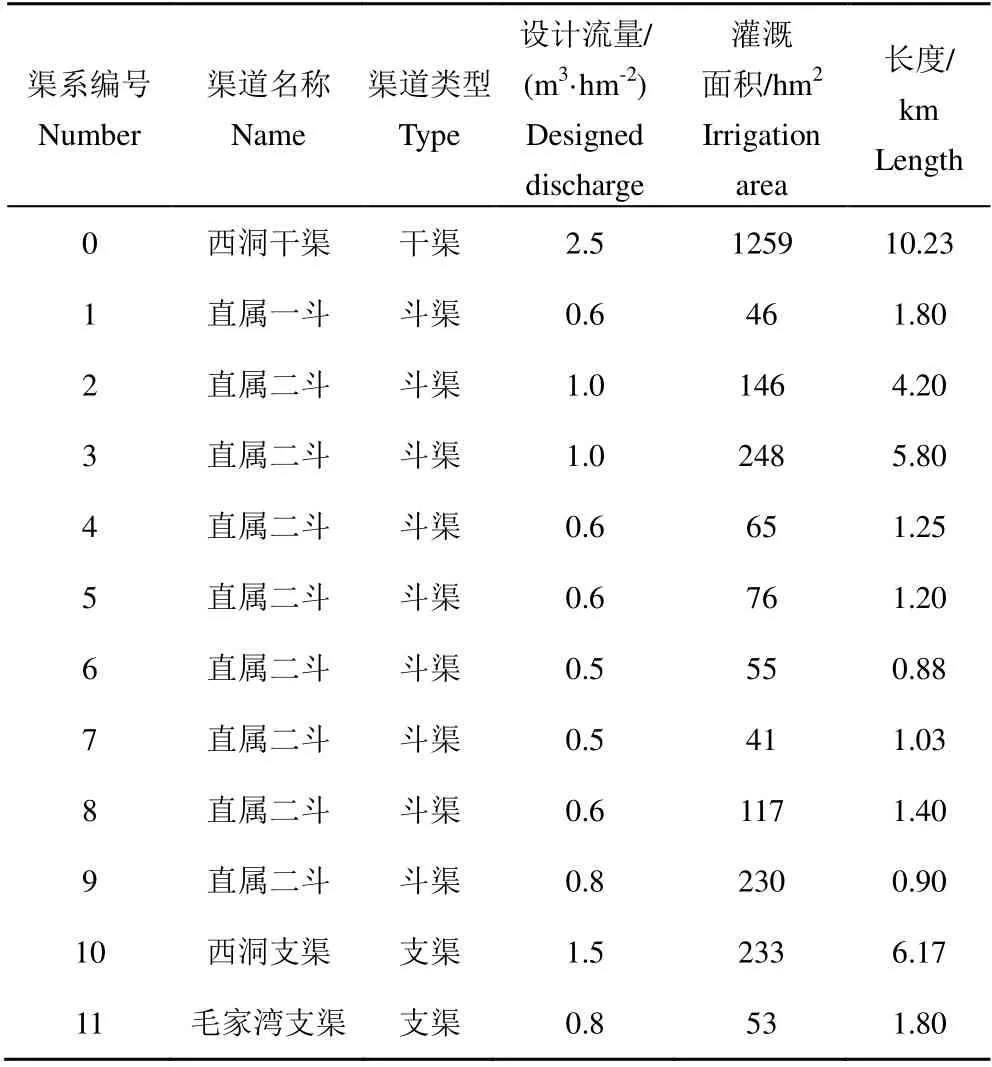
表1 渠道设计参数 Table 1 Design parameters of canal system

3 基于粒子群算法的多目标渠系优化配水模型

3.1 模型参数

结合《农田水利学》[18]，模型系数见表2。

西洞干渠共有11 条下级渠道，本文对应下级渠道将灌水起、止时间与配水毛流量设置为模型决策自变量，共33 个决策变量，同时选取包含10 000 个自变量定义域内随机初始点在内的初始点集。为使得各个粒子适应能力更强，将惯性权重定义为0.8，自我、群体学习因子定义为0.9。根据上述模型的约束分别设定灌水持续时间限制、配水毛流量区间和粒子更新速度的变化区间，进行模型的综合求解。

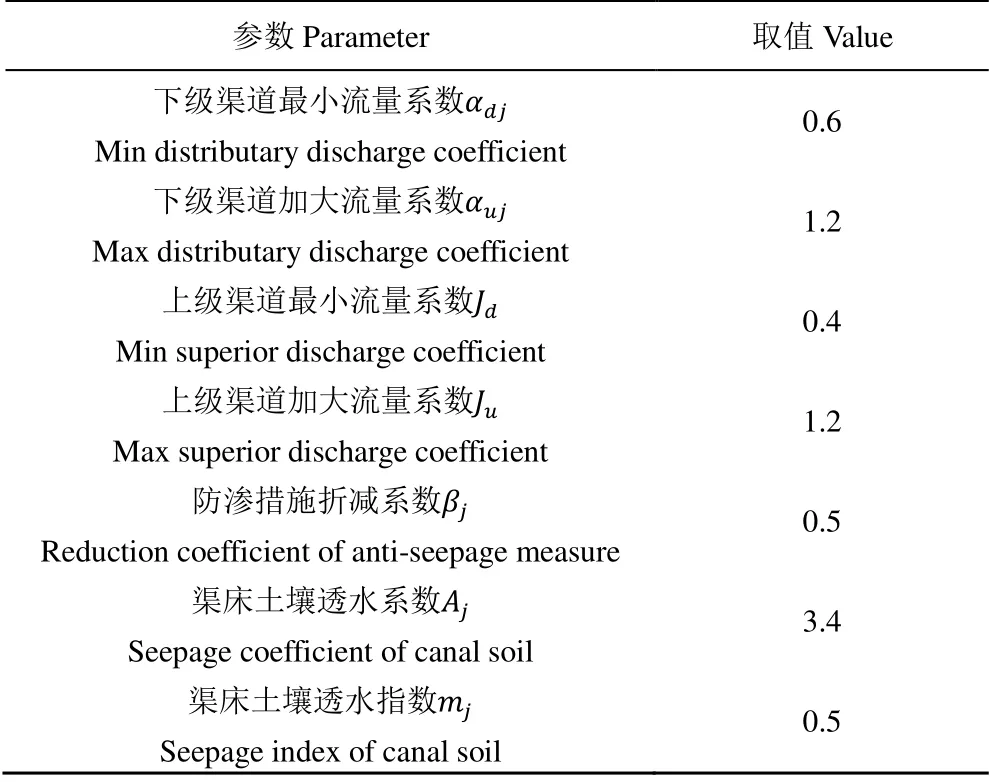
表2 渠系配水模型系数表 Table 2 The value of parameters in optimization model

3.2 求解结果

通过综合算法参数以及《农田水利学》相关参数对模型进行求解，并生成渠系灌溉配水时间如图2 所示。由图2 可知，结果结合了靠近干渠的支渠优先配水的原则，并将配水时间缩短至约11 d，相较于轮灌周期的25 d，该优化结果使配水效率得到提高。与此同时，考虑到人工开闸的延迟性问题，该结果并未在轮期一开始便进行配水，体现了结果的相对合理性。

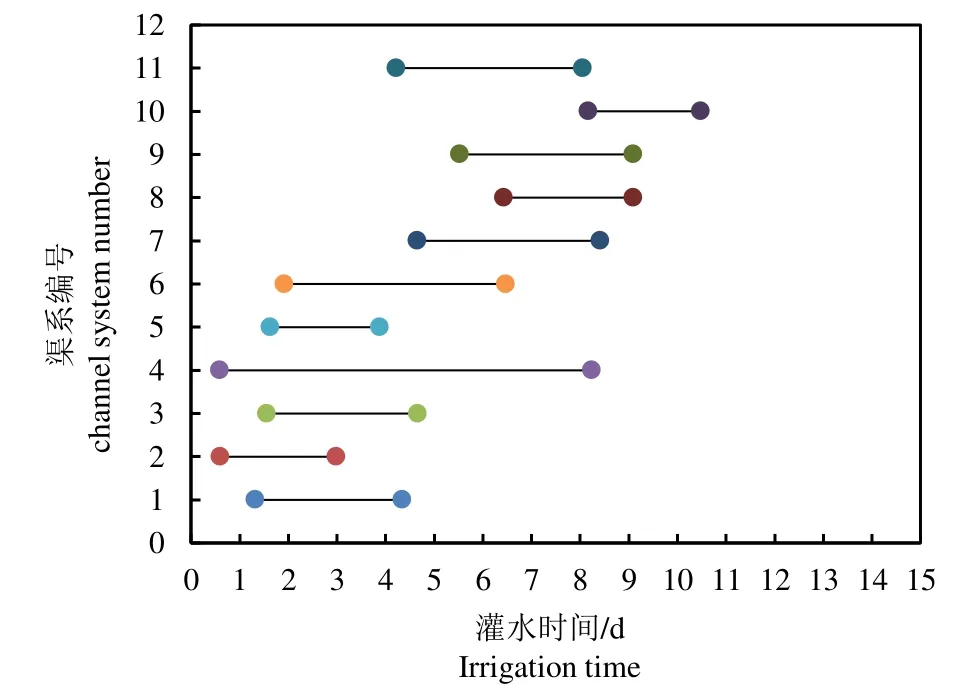
图2 西洞干渠各支、斗渠灌溉配水时间分布 Fig.2 Irrigation time distribution in branch channels of Xidong main canal

优化后各渠道的流量及流速分别如图3 及图4 所示。从图3、图4 可以看出，模型优化流量处于渠道对应的不冲不淤流量范围内，并满足贴近设计流量大小的需求。其中，直属二斗、直属五斗渠道流量几乎与设计流量一致，其余渠道的流量也略低于设计流量，间接地反映了支渠灌溉的保守性。

相较于配水计划中上级渠道的平均输水流量1.298 m3/s 而言，优化后的渠系配水模型中，上级渠道最大流量达到3.71 m3/s，配水平均流量为2.31 m3/s；且整体流量水平提高，反映了干渠流速增加是配水时间显著减少的一个重要原因，同时反映了干渠流速增加是更多支渠流速叠加的结果，增加了灌溉效率。

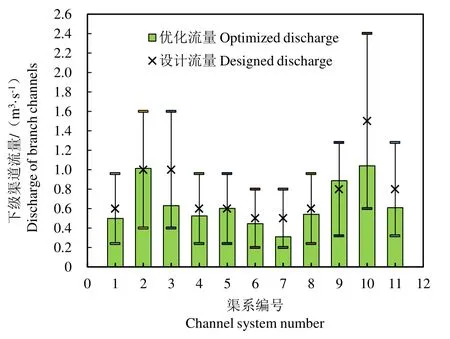
图3 西洞干渠各支、斗渠流量分布 Fig.3 Discharge distribution of branch channels of Xidong main canal

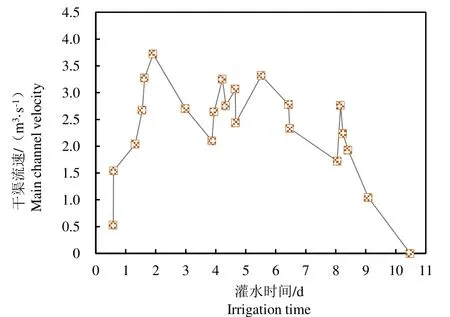
图4 西洞干渠流速变化 Fig.4 Velocity change of Xidong main canal

如图5 所示，优化后的渠系配水总量为205.07万m3，相较于配水计划总量150.8 万m3，利用率提高了35.9%；整个渠系总渗漏损失量为70.361 万m3。间接反映了良好的优化算法能合理地调整时间流量时空配置，从而有效地提高渠系水利用效率的优点。

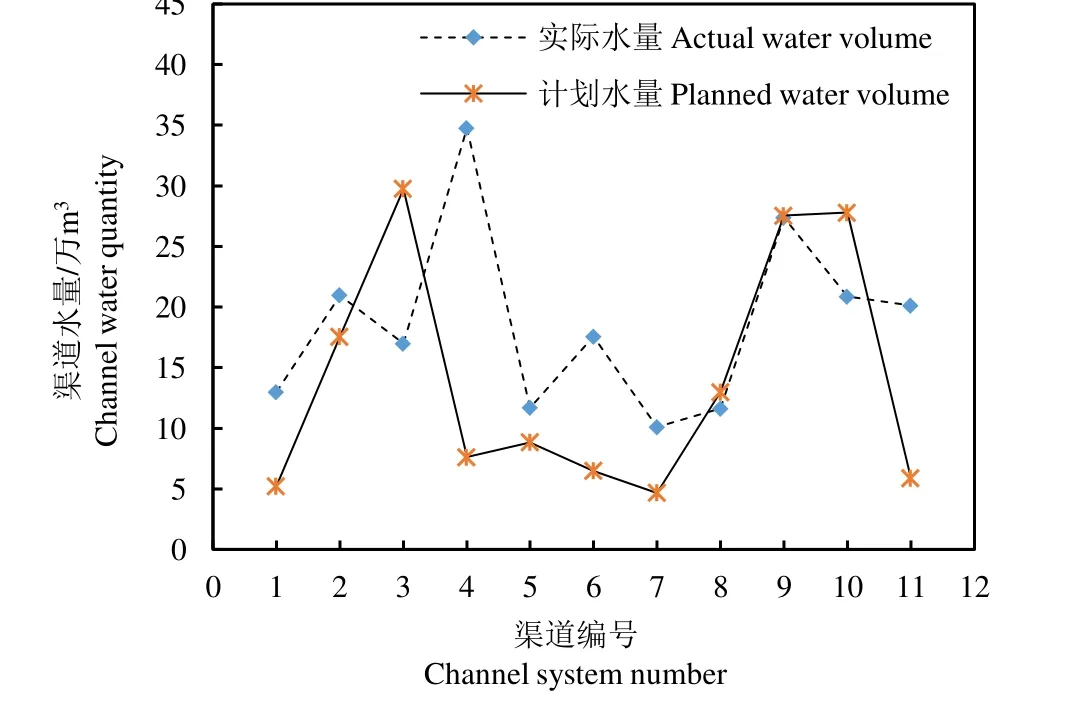
图5 西洞干渠各支、斗渠优化配水量 Fig.5 Optimal water distribution quantity of branch channels in Xidong main canal

4 3 种优化求解方法对比分析

4.1 粒子群算法与遗传算法的对比分析

在其他条件相同的情况下，按照优先满足水流平稳过渡和输水损失尽可能最小，采用向量评估遗传算法[20]（VEGA）进行过程求解。基于向量评估遗传算法得到的各支渠灌水时间如图6 所示。对比图2 与图6 可以发现，粒子群算法优化后配水时间较遗传算法更为集中，总体配水时间缩减到11 d，相比遗传算法的15 d 缩短了4 d，在单个灌水周期的约束下提高了配水的相对集中性。同时，粒子群算法体现了刚开始配水时，靠近上级渠道支渠优先配水的合理性，一定程度上提高了配水效率。

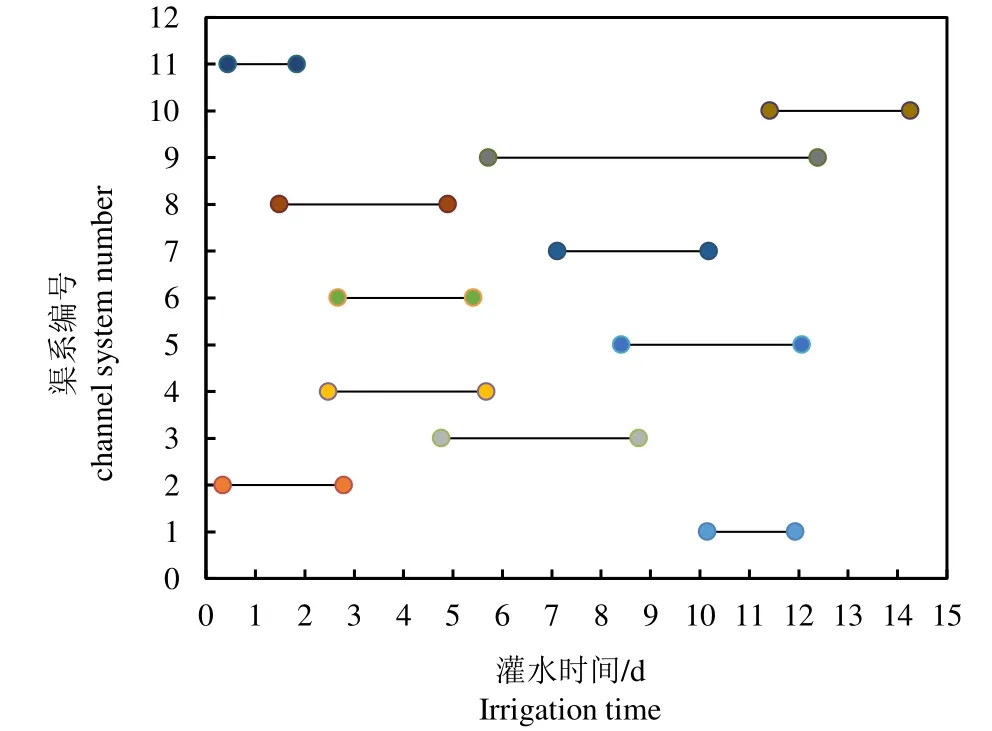
图6 基于向量评估遗传算法所得的下级渠道灌水时间 Fig.6 The irrigation time of distributary channels based on VEGA

表3 为粒子群算法与遗传算法求解的渗漏量（其中渗漏量种类包括下级渠系渗漏量、干渠渗漏量和总渗漏量）对比。由表3 可知，基于多目标粒子群算法求出的3 种渗漏量均小于向量评估遗传算法计算结果，表明粒子群算法达到全局最优解的程度更高。

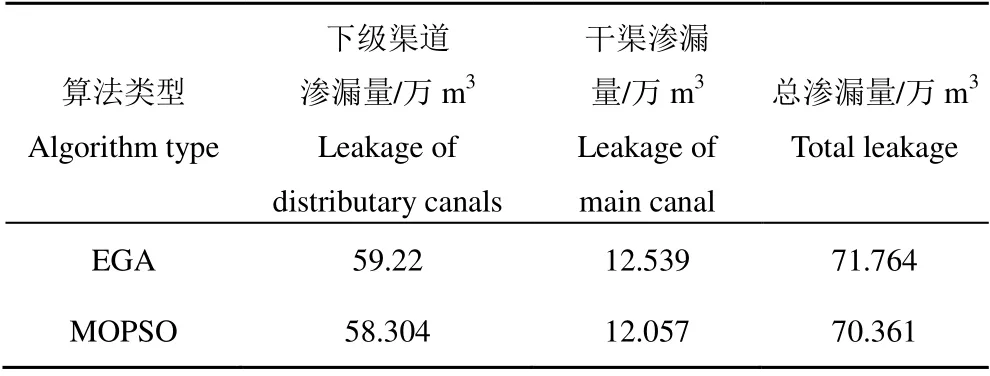
表3 利用VEGA 和MOSPO 求解的渗漏量对比 Table 3 Comparison of leakage between VEGA and MOSPO

4.2 粒子群算法与回溯法的对比分析

在干渠设计流量恒定条件下，利用回溯搜索法[21]求解各支斗渠的进水闸门开启时间，保持支渠以恒定流量连续稳定供水，当某支渠达到田间灌溉所需水量时即关闭该渠；保证其余支渠流量连续恒定条件下，再次运用回溯搜索法进行支渠选择，以此循环至所有支渠达到灌溉要求。

利用回溯搜索法求解得到渠系分时灌水如图7所示。从图2 和图7 的配水结果可以看出，配水时间方面，2 种方法都实现了相对集中配水，但多目标粒子群算法体现了近干渠先配水的合理性；从时间分布可以看出，回溯法求解结果往往在轮期刚开始即T=0时马上进行配水，考虑到人工调度以及闸门开度，这样的结果显然不合理，而多目标粒子群算法往往在第1 天的后半天进行开闸配水，充分体现了算法的合理性及对于实际生产的实用性。

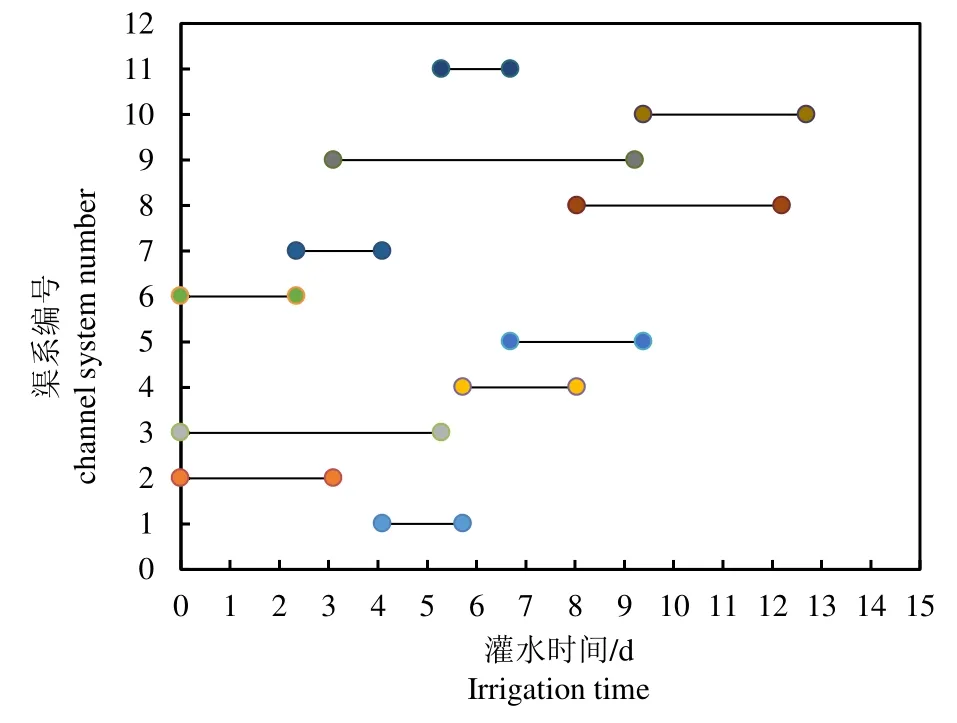
图7 基于回溯搜索算法所得的下级渠道灌水时间 Fig.7 The irrigation time of distributary channels based on BSA

5 结 论

1）将粒子群算法运用到灌区渠系优化配水模型中，可以满足渠道设计流量的要求，并且能够达到渠道总体配水时间缩短、配水集中、渗漏量少的目的，可实现集中高效配水，提高配水效率。

2）通过与向量评估遗传算法、回溯法的对比，粒子群算法展现了其良好的优化性能：与遗传算法相比，粒子群算法没有复杂的交叉变异过程，其优势在于简单容易实现，同时又有深刻的智能背景；回溯法由于其产生的弃水问题，应用限制较高，相比而言，粒子群算法能够减少弃水，能加贴近实际运行情况。

综合以上，粒子群算法在解决渠系优化配水模型求解的问题上有较高的指导意义，能够应用于灌区渠系配水管理的实践工作。