深圳地区余泥渣土强度参数的影响因素研究

武明娟,屈川翔，熊志为，郭志华，曾江波

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.香港科技大学土木与环境工程系，香港 999077；3.中南安全环境技术研究院股份有限公司，湖北 武汉 430071；4.河海大学土木与交通学院，江苏 南京 210024；5.深圳市勘察测绘院(集团)有限公司，广东 深圳 518028)

2015年深圳红坳渣土受纳场发生重大滑坡事故，造成73人死亡、17人重伤、4人下落不明，33栋建筑物被毁，经济损失高达8.81亿元[1]。经研究表明，该渣土受纳场滑坡是由于前期降雨引起坡体内含水率急剧升高，导致坡体排水系统失效而使土体强度急剧降低所致。而深圳地区余泥渣土受纳场数量多、分布广、容积大，所以研究该地区余泥渣土体的剪切强度对于此类边坡的防治有重大意义。

余泥渣土体较一般土有明显的不均匀性，土体成分复杂多样，偶见砖渣，主要来源于构筑物修建、地下工程项目施工和旧城区改造等城市化建设，土体颗粒的粒径差异较大。余泥渣土受纳场(见图1)堆积斜坡的自然沉积固结时间短，土体的密实程度不均匀，因阶段性堆填施工而存在明显的分层现象。深圳地区雨季集中，降雨量丰富，余泥渣土受纳场边坡受到降雨的影响，其含水率迅速升高，土体抗剪强度降低，则会更容易引起整个边坡的失稳，进而引发滑坡灾害。

图1 余泥渣土受纳场Fig.1 Residual soil receiving field

历年来对于土体强度的研究很多，如Lambe[2]研究认为土体压实性能和干密度相同时，最优含水率下较干侧土比湿侧土的强度和渗透性都高；Micheal[3]则研究认为非饱和状态黏土中，含水率低于最优含水率时，其黏聚力随含水率的降低而减小；Braja[4]研究认为压实膨胀土中，含水率在塑限以下，黏聚力和内摩擦角均随含水率的增高而降低，而含水率大于塑限，其内摩擦角则趋于恒定值；李振等[5]通过对干密度和细粒含量对砂卵石及碎石抗剪强度的影响的研究结果表明其内摩擦角与细粒含量有关，抗剪强度参数随干密度的增大而增大，并趋于定值；武科等[6]则通过对不同级配填土压实性能和渗透性的研究，认为填土渗透性随压实度的增大而呈现非线性减小的变化特征；王林浩等[7]、黄琨等[8]、王来贵等[9]对土体含水率和压实度展开了研究，认为土体抗剪强度的变化是含水率和压实度共同影响引起的，并得出了相应的变化规律。

深圳地区余泥渣土体具有压实度不均、粒径差异大等特点，且由于深圳地区雨季又相对集中，余泥渣土受纳场边坡失稳的概率会更高，故针对深圳地区余泥渣土体的特性，揭示其剪切强度随影响因素的变化规律极为重要。因此，本文采用正交试验设计方法，借助室内土工试验来分析多因素下余泥渣土体剪切强度的变化特征，进一步分析余泥渣土压实度与土体剪切强度、饱和渗透系数的关系，为该地区余泥渣土受纳场边坡的稳定性评价与防治工程设计提供参考。

1 正交试验原理

正交试验以概率论、数理统计和实践经验为基础，利用标准化正交试验表安排试验方案，并对试验结果进行计算与分析，最终迅速找到优化方案，是一种高效处理多因素优化问题的科学方法。该方法由统计学家田口玄一在1951年提出，在实践中逐渐被认可，已广泛拓展到各种领域，并取得了可靠的试验结果[10-14]。

正交试验设计是挑选出具有代表性的试验点进行试验，通过代表性试验结果了解全面试验的情况。代表性的试验点根据标准化正交试验表来设计，该表使正交试验具备了分散性和整齐可比性，不仅能够确定出各因素的主次效应顺序，而且可以应用方差分析对试验数据进行分析，得出各因素对评价指标的影响程度，从而找出优化条件或者最优组合，进而实现试验的目的。

2 正交试验过程与结果

2. 1 参数选取

本次试验土样取自深圳市育新小学附近的余泥渣土受纳场，所取土样的成分以人工填土为主、花岗岩和残积土为辅。由于受室内试验条件限制，本文以颗粒较小的余泥渣土体为研究对象，将其烘干、筛分，并确定试验土样颗粒级配分布曲线(见图2)。从土的颗粒级配指标来看，该试验土样属于级配良好土。为了统一土的颗粒级配指标不均匀系数Cu和曲率系数Cc，本次试验采用平均粒径d50与原样土样一致，通过改变其颗粒级配曲线的陡缓程度来进行分析。鉴于细粒土含量对于土的工程地质性质影响显著，故将大于平均粒径d50的土颗粒含量基本保持一致，而对于小于平均粒径d50的土颗粒含量改变较大。试验采用的5种土样的颗粒级配分布曲线见图2。

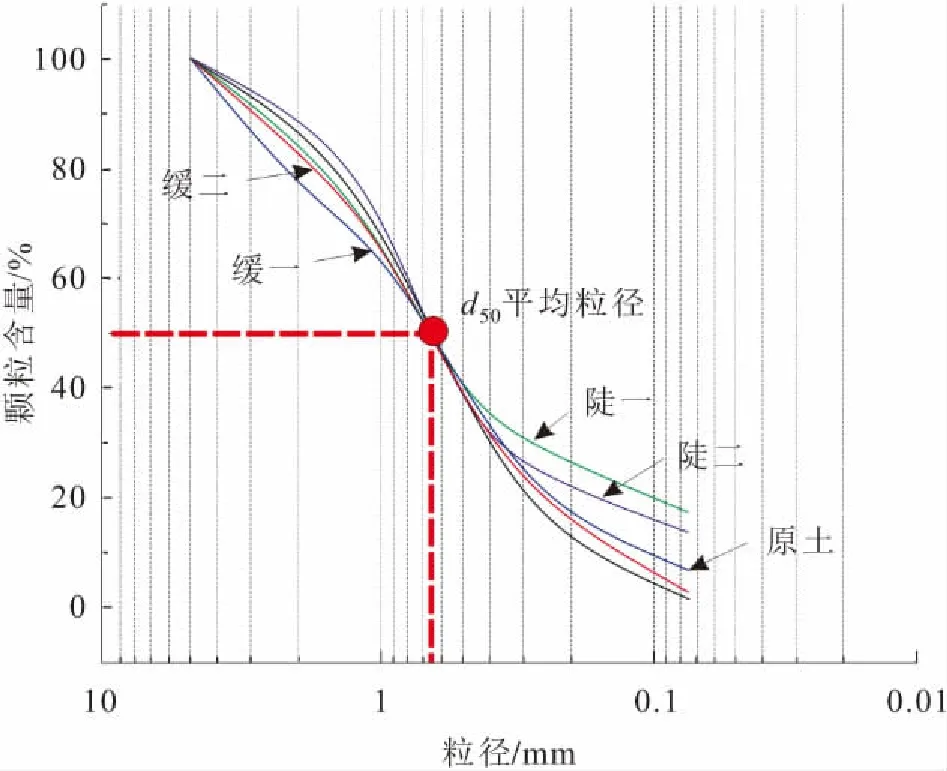
图2 试验土样颗粒级配分布曲线图Fig.2 Particle size distribution curves of the test soil samples

暴露于自然界中的斜坡，受到降雨、蒸发等自然因素的影响，土体的含水率变化较大。结合一般砂土的工程地质性质和前人的研究成果，为了揭示不同含水率下余泥渣土体剪切强度的变化规律，本试验将土体含水率的变化范围设定为10%～18%，梯度为2%，见表1。

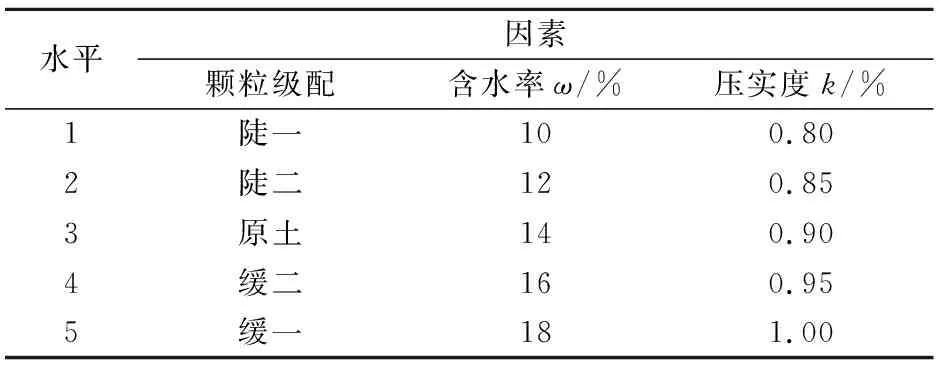
表1 试验因素水平表

土体的密实程度用压实度k表示，其计算公式如下：

k=ρd/ρd(max)

(1)

式中：ρd为土样干密度(g/cm3)；ρd(max)为土样最大干密度(g/cm3)，由土样标准轻型击实试验确定。

根据相关的渣土边坡规范和相关文献[9]，将土体的压实度范围控制在0.80～1.00之间，梯度为0.05。

2. 2 正交试验方案

2.2.1 正交试验表的确定

试验因素为颗粒级配(A)、含水率(B)和压实度(C)3个，即m=3，各因素水平均为5，即n=5。该正交试验为三因素五水平的同水平试验，自由度总和为3×(5-1)=12，采用L25(56)的正交试验表进行试验，并选择三列(2、4、5)为因素参数列，剩下三列(3、6、7)作为误差列进行误差分析，见表2。

表2 正交试验表

2.2.2 试验步骤

本次正交试验具体步骤如下：

(1) 烘干土样，进行筛分后绘制原始土样的颗粒级配分布曲线，并确定土样颗粒级配、含水率和压实度的变化范围。

(2) 选择标准正交试验表，确定因素所在列和误差分析列。

(3) 对于5种颗粒级配的土样进行配比，利用搓条法得出土样的塑限，并通过土样标准轻型击实试验，确定5种颗粒级配的重塑土样的最大干密度和最优含水率。

(4) 采用击样法制备重塑土样25种，每种土样制备4个，共计100个重塑土样。

(5) 采用常规直剪仪进行不排水不固结剪切试验，分别得出25种重塑土样在竖向荷载分别为100 kPa、200 kPa、300 kPa、400 kPa下的剪切位移量，并得出其抗剪强度指标黏聚力c和内摩擦角φ。

(6) 运用SPSS数值分析软件进行正交试验分析，分别对土样黏聚力c和内摩擦角φ进行显著性分析，得出3个因素对于土体抗剪强度各指标的一般性影响规律。

2. 3 试验结果

2.3.1 塑限试验

根据击实试验的土样粒径要求，对小于5 mm土颗粒的比例重新配比，即为等效原土的土样。保持平均粒径d50不变，通过控制土样颗粒级配曲线的陡缓来研究颗粒级配对土样抗剪强度参数的影响。上陡下陡第一种简记为“陡一”，上陡下陡第二种简记为“陡二”，上陡下缓第一种简记为“缓一”，上陡下缓第二种简记为“缓二”，等效原土比例的简记为“原土”，5条颗粒级配曲线的陡缓程度见图2。取不同颗粒级配下的干土样适量，通过搓条法进行塑限试验，测得其塑限数值，其结果见图3。

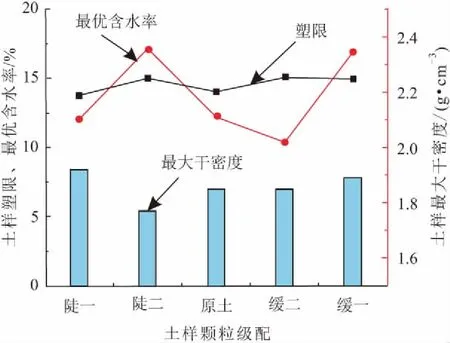
图3 试验土样的塑限、最优含水率和最大干密度分布图Fig.3 Plastic limit,optimal moisture content and maximum dry density distribution of the test soil samples

2.3.2 击实试验

根据土样塑限数值，分别制备不同颗粒级配下的5种含水率土样，其中土样含水率中值等于塑限，两个较大值高于塑限，两个较小值低于塑限，每两个值的梯度为2%。为了减小试验误差，采用喷壶喷洒土样，并采用保鲜膜防止水分蒸发，通过静置24 h使土样和水分充分混合。

试验土样分3层击实，每层25击，击实后，擦拭干净击实筒外壁，称重击实筒与试样总质量，计算试样湿密度，并取2个试样点进行试样含水率的测定，根据试样含水率和湿密度的数值，计算该含水率下的干密度。

本文采用冯忠居等[14]提出的插值函数计算法来求得土体的最优含水率w和最大干密度ρd。假设土体ρd与ω的关系曲线为抛物线型(见图4)，其关系式满足下式：

L2(w)=C0ρd0+C1ρd1+C2ρd2

(2)

式中：ρd0、ρd1、ρd2分别为土体湿密度计算结果中较大者；C0=(w-w1)(w-w2)/(w0-w1)(ω0-ω2),C1=(w-w0)(w-w2)/(w1-w0)(w1-w2),C2=(w-w0)(w-w1)/(w2-w0)(w2-w1);w0、w1、w2分别为土体湿密度对应的含水率。

通过对L2(w)求导，一阶导数的零点即为土样的最优含水率，其对应的函数值即为土样的最大干密度ρd(max)，其结果见图3。

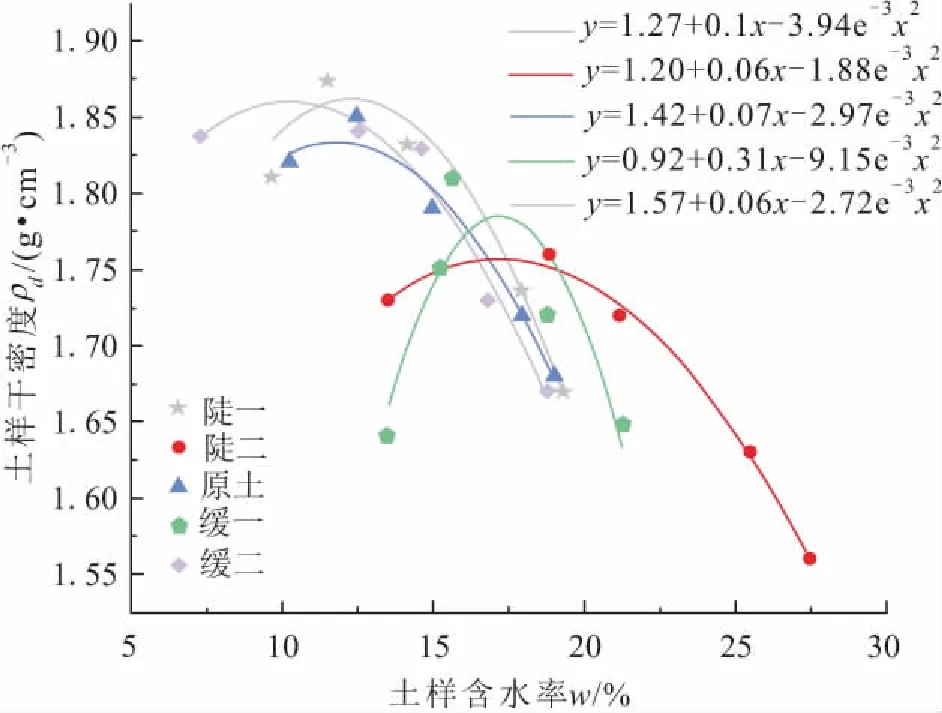
图4 试验土样击实试验的拟合曲线图Fig.4 Fitting curves of density distribution in the compaction test of the test soil samples

2.3.3 直剪试验

采用击样法制备重塑土样，同一种参数的环刀样制作4个重塑土样，开展4种不同竖向荷载δ下的直剪试验，得出试验土样的剪切强度τ以及黏聚力c和内摩擦角φ[15]，其结果见图5。

2.3.4 正交试验结果

试验土样的正交试验结果，见表3。

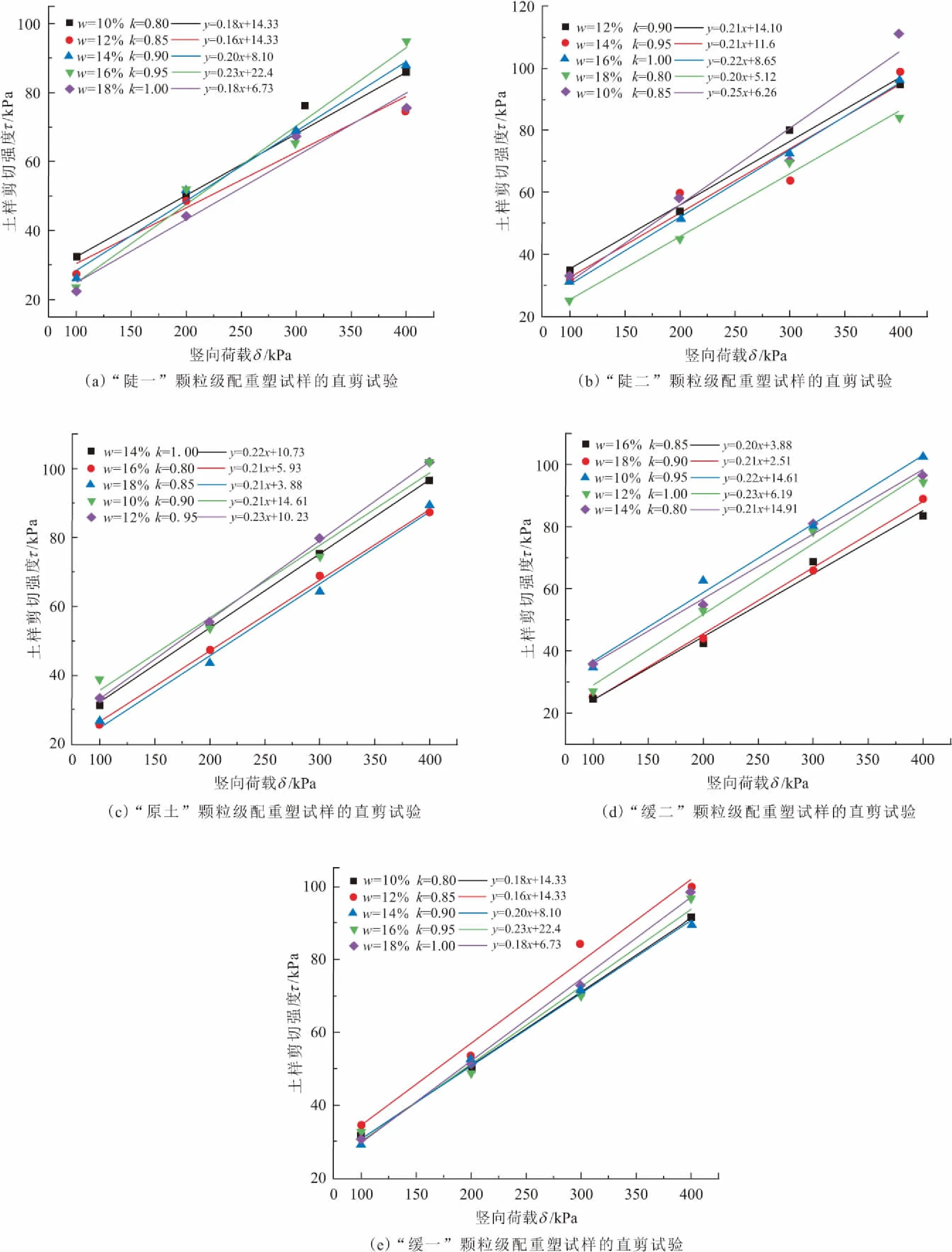
图5 试验土样正交试验的剪切曲线Fig.5 Orthogonal test shear curves of the test soil samples

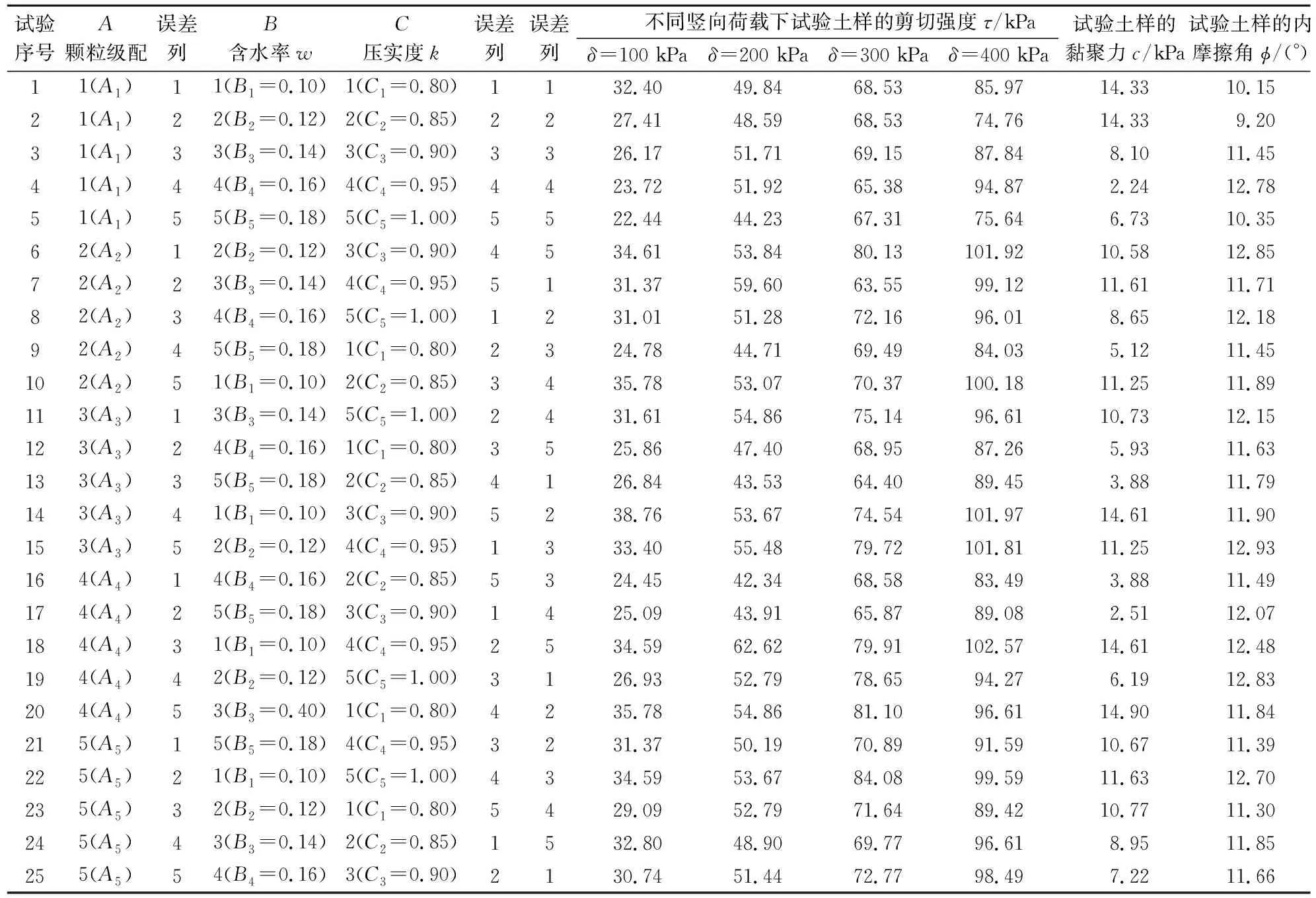
表3 试验土样的正交试验结果

3 正交试验结果分析

3.1 试验土样黏聚力c的正交试验结果分析

3.1.1 极差分析

极差分析是因素中最好水平与最差水平的指标之差，是度量数据波动大小的一个重要指标[16]。极差越大，表明该因素的水平改变对于试验结果的影响越大，即极差最大的因素即为最主要的影响因素；反之，则可认为在本次试验中，该因素的水平改变对于试验结果的影响较小。

对试验土样抗剪强度指标黏聚力c的正交试验结果进行了极差分析，其结果见表4。其中，Kij表示因素i第j水平的试验指标值;Yijk表示在因素i第j水平下的第k个试验结果，则有:

(3)

kij=Kij/n

(4)

其中,n=5；i=A、B、C；j=1,2,…,n；k=1,2,…,n。

评价因素显著性的参数为极差Ri,其计算公式为

Ri=max{Ki1,Ki2,…,Kin}-min{Ki1,Ki2,…,Kin}

(5)

由表4可知，极差最大的因素为含水率，故含水率为影响土样黏聚力c的主要影响因素，次要影响因素依次为压实度和颗粒级配。

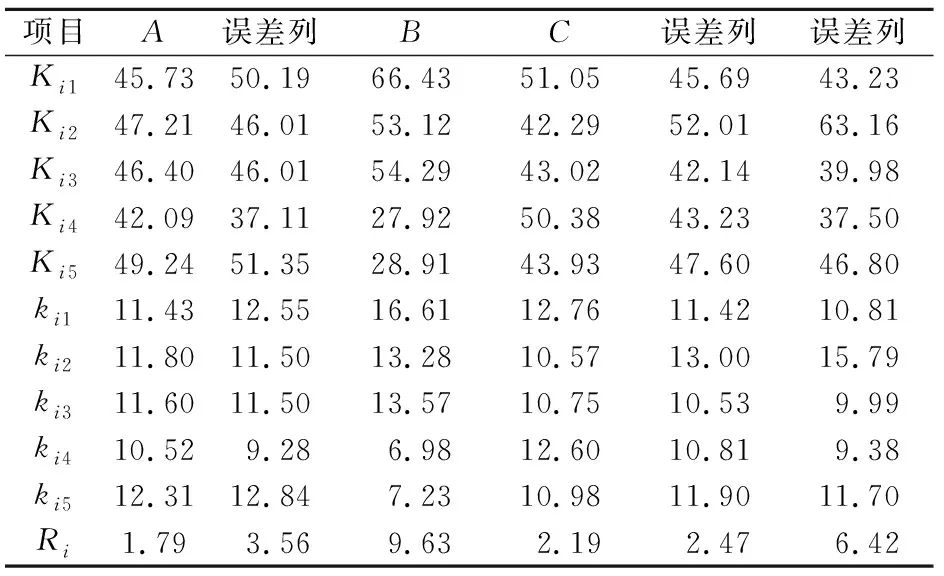
表4 试验土样抗剪强度指标黏聚力c的极差分析结果

为了能够形象直观地比较这三个因素对于试验土样抗剪强度指标黏聚力c的影响，绘制出了试验土样抗剪强度指标黏聚力与各影响因素每个水平均值的关系曲线，见图6。

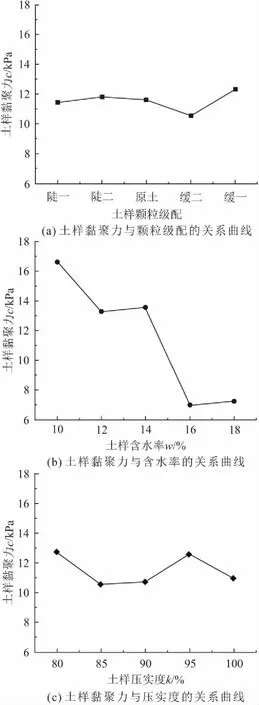
图6 试验土样抗剪强度指标黏聚力c与各影响因素的 关系曲线Fig.6 Relationship between shear strength parameter cohesion c of the test soil samples and the influencing factors

由图6可见，当颗粒级配为“缓二”、含水率为10%、压实度为95%时，试验土样的抗剪强度指标c达到最大值。

3.1.2 方差分析

方差分析与极差分析相比，能够正确地分析出引起试验数据波动的原因是试验条件改变或者试验误差。对试验土样抗剪强度指标黏聚力c的正交试验结果进行了方差分析，其结果见表5。

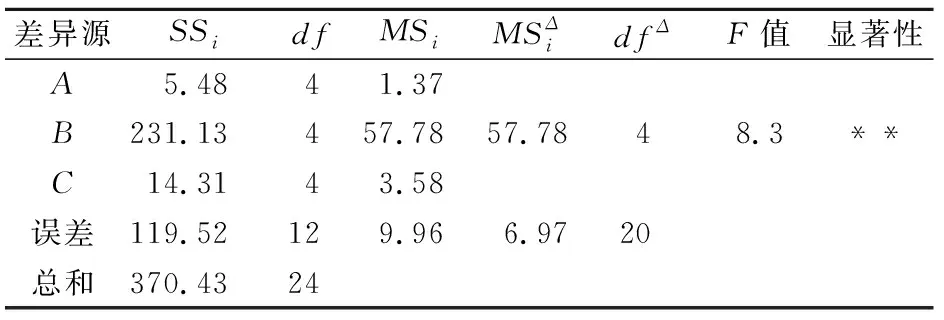
表5 试验土样抗剪强度指标黏聚力c的方差分析结果

由表5可知，有MSA≪MSe(误差列均差)、MSC≪MSe，所以对数据进行了校正，将因素A和因素C的偏差平方和并入误差平方和，该两个因素的自由度也归于误差平方和的自由度；FB=8.3>F0.05(4,20)=2.87，故在显著性水平为0.05时，因素B即含水率对于试验土样抗剪强度指标黏聚力c的影响显著性高。

3.2 试验土样抗剪强度指标内摩擦角φ的正交试验结果分析

3.2.1 极差分析

对试验土样抗剪强度指标内摩擦角的正交试验结果进行了极差分析，其结果见表6，并绘制试验土样抗剪强度指标内摩擦角φ与各影响因素每个水平均值的关系曲线，见图7。

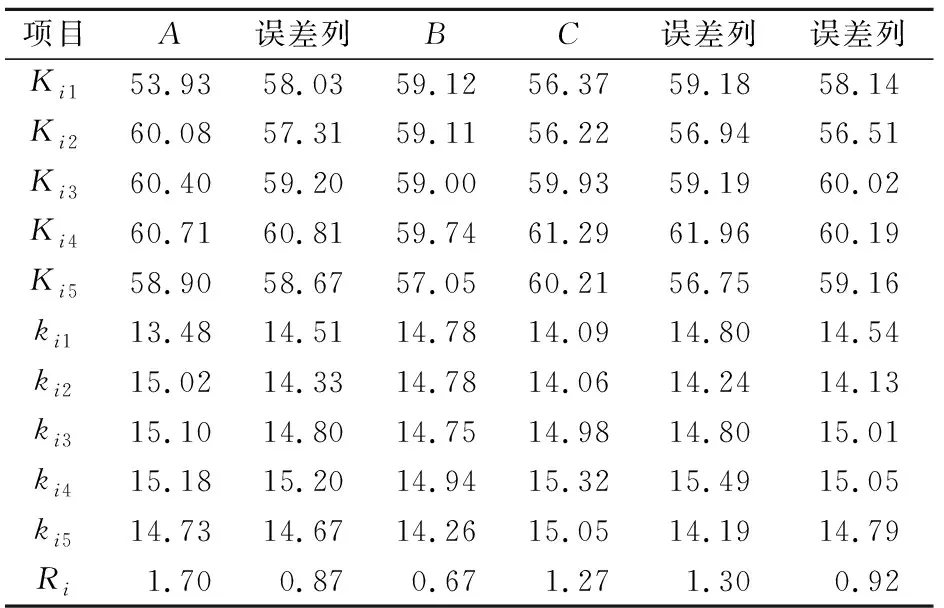
表6 试验土样抗剪强度指标内摩擦角φ的极差分析结果

由表6和图7可见，RA>RC>RB，因素A颗粒级配的数据点散布较大，即可认为颗粒级配是影响试验土样抗剪强度指标内摩擦角φ的主要因素；因素c压实度的数据点散布相对较小，其影响力则也相对较小；在3个因素中，因素B含水率的数据点散布最小，即认为该因素对于试验土样抗剪强度指标内摩擦角φ的影响最小。综上所述，对试验土样抗剪强度指标内摩擦角φ的影响程度从强到弱依次为A>C>B。

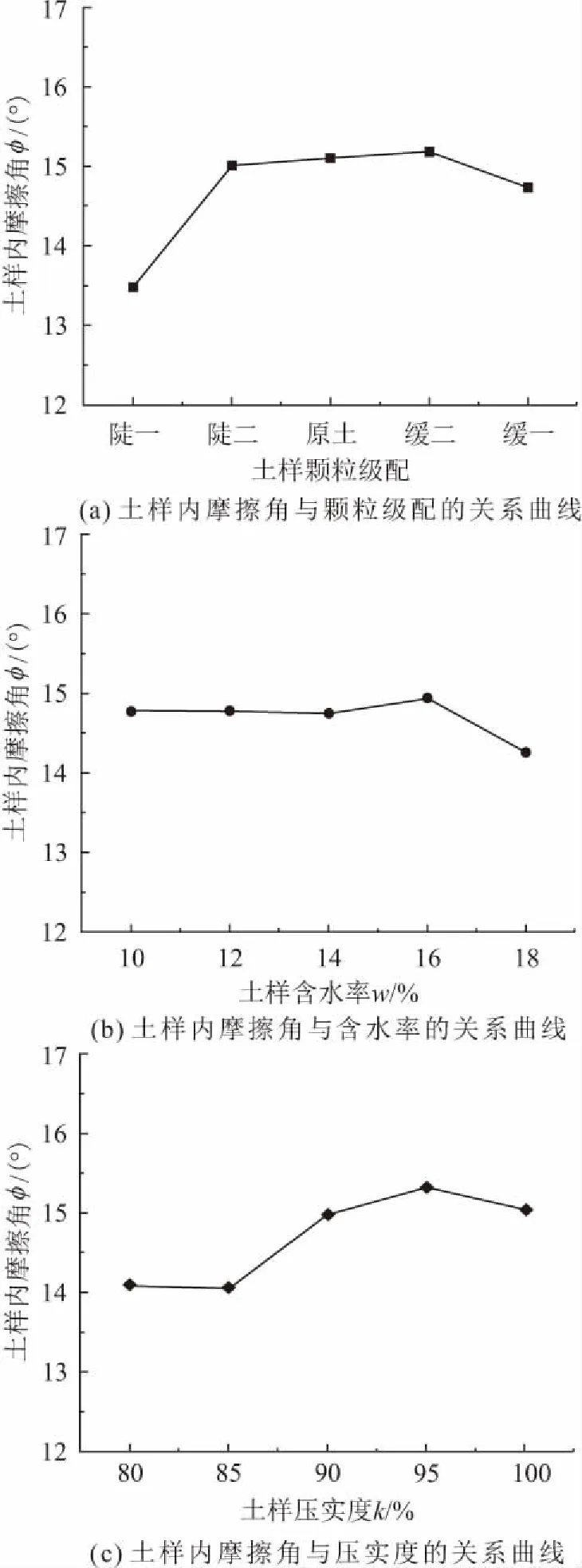
图7 试验土样抗剪强度指标内摩擦角φ与各影响因素 的关系曲线Fig.7 Relationship between shear strength parameter internal friction angle φ of the test soil samples and the influencing factors

由图7还可以看出，当含水率为16%、颗粒级配为“缓一”、压实度为95%时，试验土样的抗剪强度指标内摩擦角取得最大值。

3.2.2 方差分析

对试验土样抗剪强度指标内摩擦角φ正交试验结果进行了方差分析，其结果见表7。

表7 试验土样抗剪强度指标内摩擦角φ的方差分析结果

由表7可知，有MSB≪MSe，所以对数据进行了校正，将因素B的偏差平方和并入误差平方和，该因素的自由度也归于误差平方和的自由度；FA>F0.05(4,16)=3.01，故在显著性水平为0.05时，因素A即颗粒级配对于试验土样抗剪强度指标内摩擦角φ的影响显著性高，而因素C即压实度的影响并不显著。

3.3 试验土样剪切强度τ的正交试验结果分析

3.3.1 极差分析

除了对试验土样抗剪强度指标黏聚力c和内摩擦角φ进行极差分析和方差分析以外，试验土样剪切强度τ本身也是反映岩土体性质的重要参数，故本文同样采用了极差分析和方差分析两种方法，对于不同竖向荷载δ下重塑土样的剪切强度值逐一进行分析，其极差分析结果见表8。不同竖向荷载下重塑土样剪切强度τ与各影响因素的关系曲线，见图8。

表8 不同竖向荷载下重塑土样剪切强度τ的极差分析结果

由表8可知，当竖向荷载为100 kPa时，因素B的极差数值最大，即对竖向荷载为100 kPa下试验土样剪切强度影响最大的因素为含水率，其次为颗粒级配，影响最小的因素为压实度；当竖向荷载为200 kPa时，同样是因素B的极差数值最大，即对竖向荷载为200 kPa下试验土样剪切强度影响最大的因素仍为含水率，其次为压实度，影响最小的因素为颗粒级配;当竖向荷载为300 kPa时，与100 kPa的情况类似，影响因素由大到小的顺序为含水率>颗粒级配>压实度；当竖向荷载为400 kPa时，极差最大即影响因素显著性最高的是颗粒级配，其次依次为含水率和压实度。

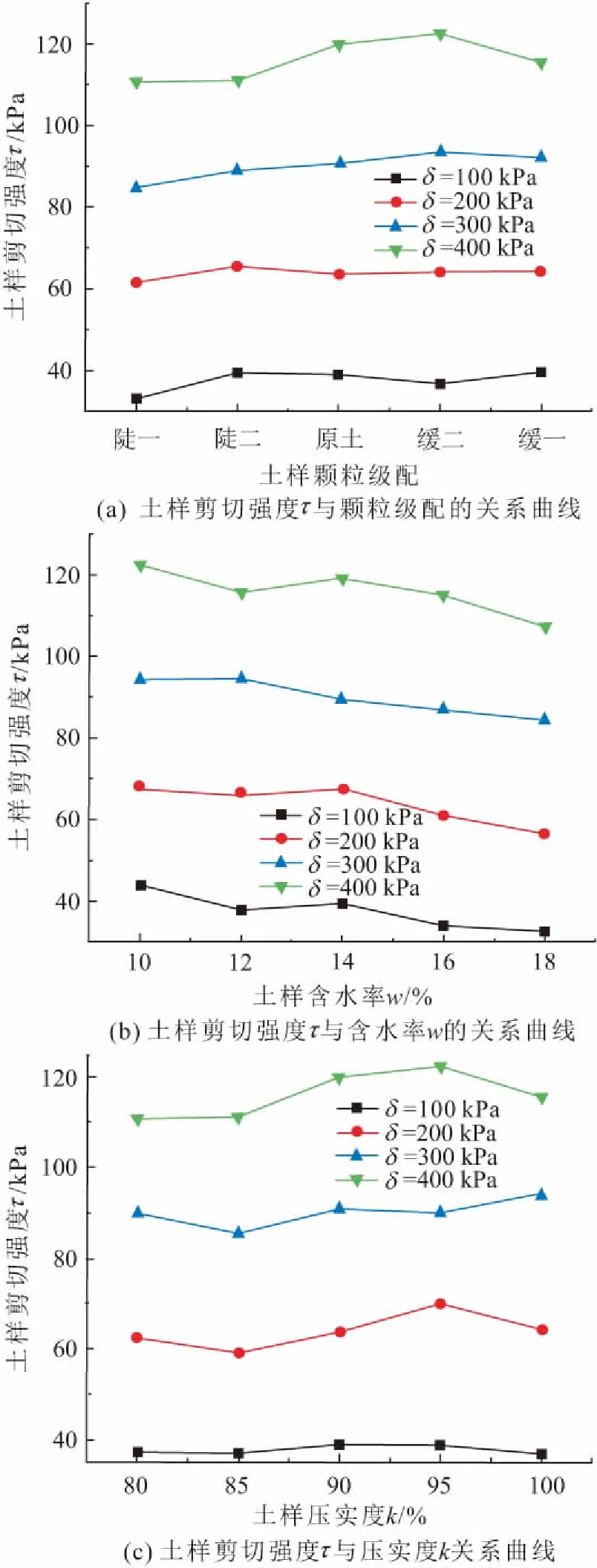
图8 不同竖向荷载下重塑土样剪切强度τ与各影响 因素的关系曲线Fig.8 Relationship between shear strength of the remoulded soil samples and various factors under different vertical loads

由图8可见，不同竖向荷载下重塑土样剪切强度与颗粒级配的变化曲线总体表现为随着颗粒级配的增加，其剪切强度在不同的竖向荷载下均呈现出不断增加的变化趋势，说明颗粒级配曲线的陡缓程度对于土体剪切强度有一定的影响[见图8(a)]；不同竖向荷载下重塑土样剪切强度与含水率的变化曲线表现为随着含水率的增加，其剪切强度在不同的竖向荷载下均呈现出不断减小的变化趋势，即含水率的增加会造成土体剪切强度的衰减[见图8(b)];不同竖向荷载下重塑土样剪切强度与压实度的变化曲线所呈现的变化规律并不一致，从压实度由0.80到0.90的变化来看，土体剪切强度均呈现先减小再增加的变化趋势，当压实度的变化范围为0.90～1.00之间时，在不同的竖向荷载下土体剪切强度的变化规律并不一致，但是总体而言均呈现先增大后减小的变化趋势[见图8(c)]。

3.3.2 方差分析

对不同竖向荷载下重塑土样剪切强度τ的正交试验结果进行了方差分析，其结果见表9。

表9 不同竖向荷载下重塑土样剪切强度的方差分析结果

由表9可知，当δ=100 kPa时，存在MSC≪MSe，将因素C的偏差平方和并入误差平方和，该因素的自由度也归于误差平方和的自由度，重新计算F值;当δ=100 kPa时，FB≫F0.05(4,16)=3.01，FA>F0.05(4，16)，故在显著性水平为0.05时，因素B即含水率对于重塑土样剪切强度的影响显著性较高，而因素A即颗粒级配则相对显著；当δ=200 kPa时，FB≫F0.05(4,12)=3.26，FC≫F0.05(4，12)，故在显著性水平为0.05时，因素B即含水率和因素C即压实度对于土体剪切强度的影响显著性均较高；当δ=300 kPa时，FAF0.05(4,12)=3.26，FB>F0.05(4，12)，FC>F0.05(4,12)，故在显著性水平为0.05时，3个影响因素即颗粒级配、含水率和压实度对于土体剪切强度的影响显著性均较高。

4 讨 论

从正交试验的结果来看，对试验土样抗剪强度指标黏聚力影响最大的因素是含水率，对试验土样抗剪强度指标内摩擦角影响最大的因素是颗粒级配，而对于试验土样剪切强度的影响因素比较复杂，但从整体来讲，影响最为显著的因素同样是含水率。由此可见，含水率对于深圳地区余泥渣土体抗剪强度特性的影响非常显著，相比而言，压实度对余泥渣土体抗剪强度特性的影响稍弱于含水率。

对余泥渣土受纳场边坡稳定性起决定性作用的是物源区域的余泥渣土，从工程实践来看，人为干预边坡土体含水率而防护边坡的措施实施起来较困难，而控制余泥渣土的密实度即压实度则是相对容易实现的，而且其密实度控制会影响工程量的大小，更重要的是余泥渣土压实度直接影响着边坡的稳定性，所以讨论密实度对余泥渣土剪切强度的作用机制对工程实践具有重要意义。

从余泥渣土受纳场边坡来看，压实度是其区别于自然边坡的显著特征，在余泥渣土受纳场的堆积过程中，每层土体堆积后即可采取碾压、夯实等方法控制各个分层土体的密实度，且操作简便。因此，研究其压实度与抗剪强度的关系对于余泥渣土受纳场边坡的防护具有十分重要的作用[17-18]。故本文在上述研究的基础上，开展了压实度与余泥渣土体强度特性和渗透特性的相关试验，重点研究压实度k取值在0.90～1.00范围时，余泥渣土体抗剪强度指标c、φ和饱和渗透系数K(sat)的变化规律。

4. 1 剪切强度与试验土样压实度的关系分析

为了研究压实度k对于余泥渣土体抗剪强度τ的影响，选取试验土样的颗粒级配为缓一、含水率为14%，其压实度分布在0.90～1.00之间，梯度为0.02，用击样法制备扰动土的重塑试样，共计6组，每组5个重塑试样，然后依次完成不固结不排水剪切试验，试验土样的剪切试验结果见图9。

图9 不同压实度下试验土样的剪切曲线Fig.9 Shear curves under different compaction degrees

不同压实度下试验土样抗剪强度指标黏聚力和内摩擦角的变化曲线，见图10。

图10 不同压实度下试验土样黏聚力c和内摩擦角 φ的变化曲线Fig.10 Change curve of cohesion c and internal friction angle φ of the test soil samples under different compaction degrees

由图10可见，试验土样黏聚力c与压实度k大致呈抛物线型的函数关系，其随着压实度的增加而不断增大，当压实度接近最大值，即试样的干密度接近最大干密度时，试验土样黏聚力的增长速度变缓，逐渐趋于某一个定值；试验土样内摩擦角φ随压实度k的变化并不很大，浮动范围很小，大致呈抛物线的函数关系，而且在研究的压实度范围内其存在最小值，即k=94%时，试验土样的内摩擦角φ最小，其值为12.05°。

由库仑定律可知，在同一竖向荷载压力下，土体剪切强度主要受黏聚力的影响较大，所以假设竖向荷载为单位1，拟合得到试验土样剪切强度与压实度的关系曲线，见图11。

图11 δ=1时试验土样剪切强度τ与压实度k的 拟合关系曲线Fig.11 Relationship between shear strength τ and compaction degree k of the test soil samples at δ=1

由图11可见，试验土样剪切强度与压实度呈抛物线型的函数关系，随着压实度增加，土体剪切强度值逐渐增大至某一定值。

该试验结果与王来贵等[9]的研究结果相互印证，岩土体抗剪强度随着压实度的增加而呈线性上升，岩土体黏聚力逐渐增大，内摩擦角增加较小。同样，李振等[5]在对河床卵石的试验过程中也得到类似的结论，即土体抗剪强度参数随着干密度的增加而增大，最终趋于某一定值。而在王林浩等[7]在黄土的试验研究中也得出类似的结论，压实黄土状粉土的抗剪强度指标c、φ值均随干密度的增加而增大。

4. 2 饱和渗透系数与压实度的关系分析

为了研究压实度对于余泥渣土渗透能力的影响，选取与研究强度特性相同的渣土重塑试样，进行了变水头渗透试验，其试验结果见图12和图13。

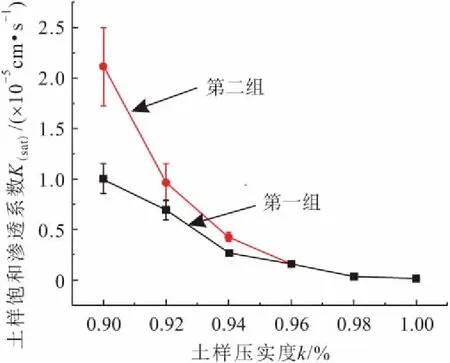
图12 试验土样饱和渗透系数与压实度的关系曲线Fig.12 Relationship betweensaturated permeability coefficient and compaction degrees of the test soil samples

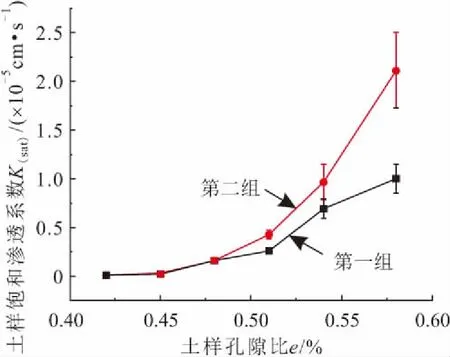
图13 试验土样饱和渗透系数与孔隙比的关系曲线Fig.13 Relationship between saturated permeability coefficient and porosity of the test soil samples

由图12可见，在研究的压实度范围内，试验土样的饱和渗透系数K(sat)与压实度k呈负相关关系，当压实度为0.90～0.94时，试验土样的饱和渗透系数急剧减小，后半段逐步平缓，即压实度增加到一定程度，试验土样的饱和含水率则会维持在一定水平。根据土体物理参数之间的内在关系，得出一定压实度下土体的孔隙比e，并根据试验数据结果，绘制试验土样饱和渗透系数K(sat)与孔隙比e的关系曲线。

由图13可见，试验土样的饱和渗透系数与孔隙比呈正相关关系，大致呈指数关系增长，即岩土中空隙体积所占比例越大，土体越疏松，而土体的饱和渗透系数也越大。本次试验研究的孔隙比范围之内，随着孔隙比的增加，试验土样饱和渗透系数的数值也越来越大。

本试验的研究结果与邵健伟等[19]的试验结果一致，对于同一粒度成分的粗粒土而言，其渗透系数随干容重的增加而减小，随相对密实度的增加而减小。而武科等[6]对于填土渗透系数与压实度的关系研究中，也同样表明填土的渗透特性随着压实度的增加而呈现非线性减小的变化规律。

5 结 论

本文采用正交试验的方法，探究了深圳地区余泥渣土体抗剪强度指标c和φ随着颗粒级配A、含水率B和压实度C的变化规律，并针对余泥渣土体剪切强度τ、饱和渗透系数K(sat)与压实度k的关系，展开了室内土工试验，得到如下主要结论：

(1) 在研究的影响因素中，对深圳地区余泥渣土体抗剪强度指标黏聚力c的影响程度从强到弱依次为B>C>A，而且在A=“缓二”、B=10%、C=95%时，土体抗剪强度指标黏聚力c达到最大值。从试验结果来看，含水率的增加会促使土体黏聚力急剧下降，降低了土体的剪切强度。

(2) 在研究的影响因素中，对深圳地区余泥渣土体抗剪强度指标内摩擦角φ的影响程度从强到弱依次为A>C>B，而且在A=“缓一”、B=16%、C=95%时，土体抗剪强度指标内摩擦角φ达到最大值。从试验结果来看，含水率的增加可能会引起土体内摩擦角的降低，而土体内摩擦角与压实度则大致呈现正相关关系。

(3) 各因素对不同竖向荷载下余泥渣土体剪切强度的影响并不完全一致，综合极差分析和方差分析结果可以认为，在不同竖向荷载下，含水率B为影响土体剪切强度τ最显著的因素，而且两者之间均呈现负相关关系，即随着含水率的增加，土体抗剪强度显著降低。

(4) 为了进一步揭示余泥渣土体剪切强度τ和饱和渗透系数K(sat)与压实度k的关系特征，开展了相关试验。试验结果表明：在压实度k研究范围内，土体内摩擦角φ和黏聚力c分别存在最小值和最大值，土体黏聚力和内摩擦角与压实度大致呈现二次函数的关系特征；土体剪切强度τ与压实度k亦呈现抛物线型关系特征，且在压实度研究范围内土体剪切强度τ存在最大值;而土体饱和渗透系数K(sat)则与压实度k呈现负相关关系，大致呈指数函数型关系特征。由此可见，密实度的增加，导致土体颗粒内部空隙减小，渗水通道被压密破坏，致使其渗透系数急剧降低。