漏喷同存地层吊灌作业安全时间研究

吕晓平,张 敏,田 径,蔡明杰

(1.西部钻探工程有限公司国际工程公司,新疆 乌鲁木齐 830013；2.西部钻探工程有限公司玉门钻井分公司,甘肃 玉门 735200;3.西南石油大学石油与天然气工程学院，四川 成都 610500)

随着深层油气的勘探开发，钻遇裂缝性储层的可能性迅速增大，裂缝性储层中常出现多压力系统，会造成频繁的钻井液漏失[1]。当钻井液漏失导致环空液面下降时，钻井液柱压力下降，可能会引发溢流，进而造成井喷事故，这种现象被称为“漏喷同存”[2]。“吊灌”技术是指钻井液漏失发生后，在一定时间内将钻井液注入井筒，以平衡井筒内的压力，从而防止井喷事故的发生[3]。其中，吊灌技术的时间间隔是平衡井筒内压力的关键因素。为了防止井喷事故的发生，国内外许多油气开发地区都广泛采用了吊灌技术，但是目前针对吊灌技术的时间间隔研究还处于起步阶段，吊灌技术的时间间隔往往由经验决定，存在较大的误差。漏喷转化时间是指钻井液从液位下降到溢流开始的时间。吊灌技术主要是控制井眼的漏失阶段，从而防止漏失与溢流之间的转换，避免造成井下事故。因此，吊灌技术的时间间隔必须小于漏喷转换时间。

在过去的几十年里，许多学者对井漏事故进行了研究。如赵良孝[4]研究指出，钻井液漏失有两种类型，即天然渗透层的漏失和重泥浆压裂诱导缝的漏失；Yuan等[5]基于事故致因理论，建立了钻井井漏的概念模型，将钻井井漏的风险源分为地质条件、井底压力、漏采因素和打捞失效，并推断地质因素是钻井井漏的最大影响因素；王贵等[6]建立了诱导裂缝性漏失堵漏的断裂力学模型，研究了堵漏材料在不同封堵位置对阻止诱导裂缝延伸的影响，并指出堵漏材料在裂缝入口较短距离内的封堵为封堵诱导裂缝延伸的最佳位置；Shi等[7]分析了地层破裂压力与井漏压力之间的关系，指出地层破裂压力不能代替井漏压力；Verga等[8]提出了一种检测天然裂缝的新方法，并指出单一天然裂缝与网格结构的天然裂缝在漏失特性上是不同的；刘绘新等[9]采用井筒漏失动态分析方法,建立了吊灌作业安全时间数学模型,并给出了多种漏失速率的积分结果，结果表明适当增加吊灌量可以增加吊灌作业安全时间，适当减少吊灌钻井液密度也可以增加吊灌作业安全时间；贾红军等[10]分析了钻遇多压力系统裂缝性气层形成溢流和漏失并存的问题，并建立了多压力系统裂缝性气层溢漏同存的物理模型，结果表明溢漏同存时井筒环空压力迅速下降，溢流态势更加严重，且井筒环空的液体流量急剧减少,气体迅速向上滑脱和运移,导致气液两相流型分布变化较大；舒刚等[11]针对直井钻遇单条裂缝时由于重力置换而引起的漏喷同存问题,建立了气相模型和液相模型,并通过气液分界面将这两个模型耦合起来，模型计算与试验验证结果表明,对漏失速率和气体溢流量影响最大的因素是缝宽,其次是压差、钻井液流变性能；晏凌等[12]针对碳酸盐岩裂缝性储层在钻井过程中极易发生喷漏同存的复杂情况，引入精细控压钻井技术在四川盆地GS19井的窄密度窗口超高压二叠系栖霞组进行了成功应用。

目前关于多压力系统裂缝性地层漏喷同存问题的研究并不多，多为定性、半定量化地研究漏喷同存问题出现的原因和针对喷漏同存采取的堵漏压井技术,缺乏针对裂缝性地层漏喷转换时间的深入研究。本文的目的是研究漏喷同存裂缝性地层的漏喷转换时间，建立了多压力系统裂缝性地层漏喷转化时间计算模型，并通过再现明格油田现场数据和已发表文献的模拟结果，对模型进行验证。在此基础上，对漏喷转换时间的影响因素进行了研究，以期研究成果能为现场吊灌作业安全时间的选取提供指导。

1 多压力系统裂缝性地层漏喷转换时间计算模型

当钻遇裂缝性储层时，储层中常出现多压力系统，会造成频繁的钻井液漏失。钻井液发生漏失后，由于钻井液漏失循环，井筒内的钻井液液位将会下降，这会导致高压地层上方的有效液柱压力降低。当有效液柱压力小于高压地层的压力时，高压地层的流体将从地层中溢流到井筒中，这就形成了漏喷同存现象。对于多压力系统裂缝性地层来说，漏失层和高压层可以位于同一地层，也可以位于不同地层，如图1所示。

图1 多压力系统裂缝性地层漏喷同存现象的 物理模型Fig.1 Physical model of leakage-overflow-coexistence in fractured stratum with multi-pressure system

基于以下假设，本文建立了漏喷转换时间计算模型：①仅存在一个漏失层，而高压层中的一层或多层中有可流动的流体；②漏失层有一个水平裂缝；③钻井液呈层流流动，垂直方向的裂缝值可忽略不计；④钻井液的流变特性在流动过程中不改变。

图2 一维径向裂缝中钻井液的流动模型Fig.2 Flow model of the drilling fluid in one-dimensional radial fracture

如图2所示，在上述模型假设的前提下，钻井液向裂缝横向延伸r方向流动的连续性方程为

(1)

式中：w为裂缝初始宽度(mm)；r为裂缝横向延伸距离(mm)；t为时间(s)；v为钻井液流速(mm/s)。

动量守恒方程为

(2)

式中：ρ为钻井液密度(kg/m3);vr为沿r方向钻井液流速(mm/s)；τ为钻井液动切力(Pa)，其下标表示方向;z为裂缝纵向延伸长度(mm)。

偏微分方程为

(3)

式中:n为钻井液流性指数(无量纲)；K为钻井液稠度系数(Pa·Sn)；p为压力(MPa)。

结合方程(1)、(2)和(3)，可以得到流体压力梯度与钻井液漏失速率(V)之间的关系式如下:

(4)

式中：V为钻井液漏失速率(m/s)。

对上式采用牛顿-辛普森法，可以得到径向裂纹内的流体压力梯度为

(5)

当流体压力降至孔隙压力值时，钻井液停止漏失。则钻井液最大侵入深度与钻井液压降的关系式如下：

(6)

式中：pw为井底压力(MPa)；pf为孔隙压力(MPa)；rf为钻井液侵入深度(m)；rw为井筒半径(m)。

由此可以得到钻井液在径向裂缝中的漏失速率为

(7)

式中:Δp为钻井液漏失正压差(MPa)。

随着钻井液液面的下降，压力平衡方程为

pa+0.009 8ρh=pw

(8)

h=H-l

(9)

式中：pa为井口压力(MPa)；ρ为钻井液的密度(g/cm3)；h为井筒内液柱的高度(m)；H为地层的深度(m)；l为钻井液的高度降低量(m)。

因此，当地层中的流体开始溢流到井筒时，可以通过方程(8)和(9)得到井筒中的液位，并结合方程(7)、(8)和(9)可以得到径向裂缝中钻井液的漏失速率为

(10)

当钻井液发生漏失后，井筒中的钻井液液位将会降低，这会导致高压地层上方的有效液柱压力降低。当有效液柱的压力小于地层的压力时，高压地层的流体将从地层溢流到井筒，这个过程所花费的时间称为漏喷转换时间。显然，漏喷转换时间取决于钻井液的漏失速率和钻井液排量。 因此，可以得到如下等式：

(11)

式中:A为单位长度钻井液体积(m3/m)。

因此，结合公式(10)和积分求解式(11)，可以得到漏喷转换时间的计算方程为

(12)

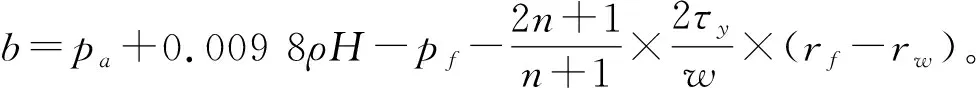
2 模型验证

为了验证上述模型的准确性，本文对明格布拉克油田明15井二开井段多压力系统裂缝性地层漏喷同存现象进行了模拟计算，其基础数据见表1。根据建立的漏喷转换时间计算模型，计算得出该井段漏喷转换时间T为397.6 s，而该井段实际漏喷转换时间大约为412 s，误差为3.5%，表明本文模型具有较高的精度，可用于多压力系统裂缝性地层漏喷转换时间的预测。

表1 明格布拉克油田明15井2开井段基本参数数据

为了进一步验证数学模型的准确性，根据文献[13]和[14]中的具体数据，将本文模型计算得到的该井段漏喷转换时间的计算结果与Shahri’ s模型和Wang’ s模型的计算结果进行了比较，其比较结果见图3。

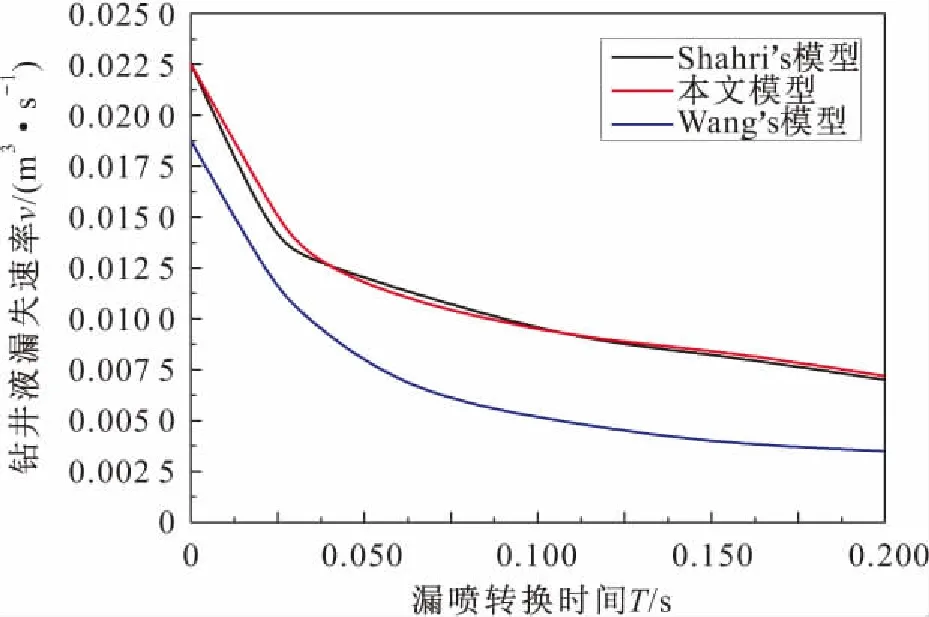
图3 本文模型与Shahri’ s模型和Wang’ s模型计算 结果的比较Fig.3 Comparison results of loss speed between proposed model,Wang’s model and Shahri’s model

由图3可见，本文模型计算曲线与Shahri’ s模型计算曲线吻合较好，但与Wang’ s模型计算曲线之间存在一定的误差，这可能是由于各自模型所采用的流体类型不同造成的，Wang’ s模型使用的是宾汉姆流体，而Shahri’ s模型和本文模型使用的是赫巴流体。

3 多压力系统裂缝性地层漏喷转换时间的影响因素分析

3. 1 钻井液流性指数对漏喷转换时间的影响

图4为漏喷转换时间与钻井液流性指数之间的关系曲线。

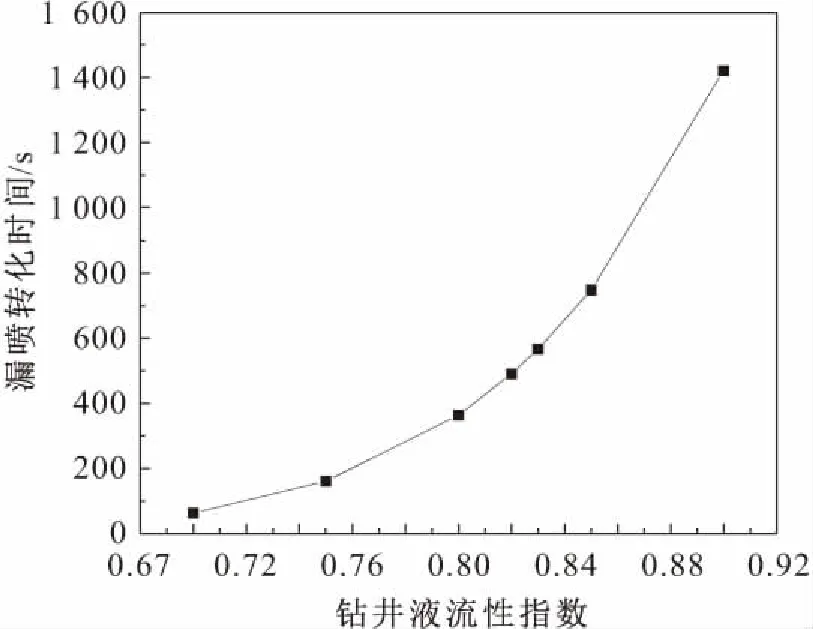
图4 漏喷转换时间与钻井液流性指数之间的关系曲线Fig.4 Relationship between conversion time between lost circulation and overflow with the liquidity index of drilling fluid

由图4可见，随着钻井液流性指数从0.80增加到0.90，漏喷转换时间显著增加，这种现象是由于随着钻井液流性指数的增加，钻井液的流动能力显著下降，导致钻井液漏失速率与地层流体溢流速度都降低，进而导致漏喷转换时间增加；当钻井液流性指数达到较高的值(例如0.9)时，钻井液几乎不会流动，漏喷转换时间显著增加。

3. 2 钻井液密度对漏喷转换时间的影响

图5为漏喷转化时间与钻井液密度的关系曲线。

图5 漏喷转换时间与钻井液密度的关系曲线Fig.5 Relationship between conversion time between lost circulation and overflow with the drilling fluid density

由图5可见，随着钻井液密度从1.34 g/cm3增加到1.42 g/cm3，漏喷转换时间呈现出增加趋势。这种现象可能归因于两个原因：其一，当钻井液密度增加时，井筒内的液柱压力将增加，导致井筒内钻井液静液柱压力增大，环空液面需要下降到更低的位置才能达到漏喷转化时间的阀值；其二，当钻井液密度较大时，其流动摩阻较大，流体流动更加困难，进一步增加了漏喷转化时间。因此，随着钻井液密度的增加，漏喷转换时间增加。

3. 3 裂缝宽度对漏喷转换时间的影响

图6为漏喷转换时间与裂缝宽度的关系曲线。

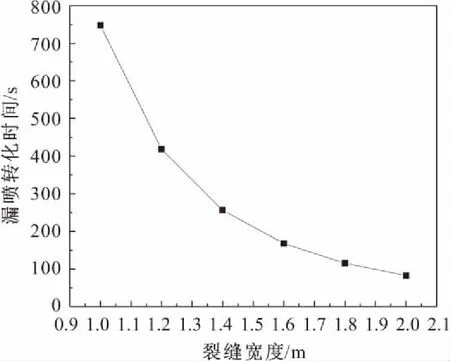
图6 漏喷转换时间与裂缝宽度的关系曲线Fig.6 Relationship between conversion time between lost circulation and overflow with the crack width

由图6可见，随着裂缝宽度从1.0 mm增加到2.0 mm，漏喷转换时间显著减少。漏失通道和存储空间是影响钻井液漏失的两个重要参数，随着裂缝宽度的增加，漏失通道将比以前更宽，钻井液的储存空间也将更大。因此，随着裂缝宽度的增加，钻井液更加容易漏失，即钻井液的漏失速率增加，漏喷转换时间降低。

3. 4 钻井液侵入深度对漏喷转换时间的影响

图7为漏喷转换时间与钻井液侵入深度的关系曲线。

图7 漏喷转换时间与钻井液侵入深度的关系曲线Fig.7 Relationship between conversion time between lost circulation and overflow with the drilling fluid intrusion depth

由图7可见，漏喷转化时间随着钻井液侵入深度的增加而显著增加。这是因为：当钻井液漏失到地层后，钻井液中的固相颗粒会堵塞地层，降低地层渗透率，且钻井液侵入深度越大，地层渗透率越低。因此，随着钻井液侵入深度的增加，钻井液从井筒进入漏失层的时间增加，漏喷转换后，地层流体进入井筒的速度也降低，漏喷转换时间大大减小。

吊灌作业的安全时间间隔必须小于理论计算的漏喷转换时间才能避免溢流甚至井喷事故的发生。因此，适当增加钻井液的流性指数和钻井液的密度可以有效地增加多压力系统裂缝性地层漏喷转换时间，确保吊灌作业的及时性，保证井控安全。

4 结 论

(1) 基于一维径向裂缝中钻井液的流动模型，建立了多压力系统裂缝性地层漏喷转换时间计算模型，通过对数学模型的求解，得到了漏喷转换时间的计算方程，并以川东北油井资料和已发表文献对模型进行了验证，结果表明：本文建立的模型具有较高的精度，可用于多压力系统裂缝性地层漏喷转换时间的预测。

(2) 漏喷转换时间随着钻井液流性指数、钻井液侵入深度和钻井液密度的增加而增大，随着裂缝宽度的增加而减小，其中钻井液流性指数对漏喷转换时间的影响最大，其次是钻井液侵入深度，而裂缝宽度和钻井液密度对漏喷转换时间的影响次之。