连续刚构桥不等长悬臂施工控制措施数值分析
陈猛

摘 要:连续刚构桥具有诸多优点,能够有效满足特大跨径桥梁的受力要求。针对某连续刚构桥悬臂不等长施工方案,本文研究长跨继续施工和短跨压重荷载之间的控制措施,解决不等跨梁桥悬臂浇筑施工过程中可能存在的偏载问题,分析不同加载方式产生的内力和变形,然后依据分析结果,提出合理的建议。
关键词:连续刚构;悬臂不等长;配重;加载
中图分类号:U448.23文献标识码:A文章编号:1003-5168(2020)23-0104-03
Abstract: Continuous rigid frame bridges have many advantages and can effectively meet the force requirements of super long span bridges. Aiming at the unequal-length cantilever construction scheme of a continuous rigid frame bridge, this paper studied the control measures between the continuous construction of long-spans and short-spans under heavy load, solved the possible eccentric load problems during the cantilever pouring of unequal-span girder bridges, and analyzed the internal forces and deformations caused by different loading methods, then put forward reasonable suggestions based on the analysis results.
Keywords: continuous rigid frame;cantilever unequal length;counterweight;loading
連续刚构桥梁墩固结、梁体连续、无伸缩缝、行车平顺,同时可以产生较大的横向抗扭刚度和顺桥向抗弯刚度,优点突出,能满足特大跨径桥梁的受力要求[1-2],因此,连续梁桥发展迅猛。随着桥梁事业的发展,近年来,悬臂施工法在国内外大跨径预应力混凝土桥梁中得到广泛运用 。
国内对于高墩大跨度变截面曲线箱梁桥等悬臂施工控制方面的研究较为成熟,但对于不等长连续刚构桥悬臂施工控制所需要采取的措施,相关研究较少。本文针对65 m+110 m+65 m连续刚构桥悬臂不等长施工方案,在两侧等跨悬臂施工完成后,研究长跨继续施工和短跨压重荷载之间的控制措施。
1 工程概况
某大跨连续刚构桥跨越两山间峡谷,谷底有一河流,桥位处河流宽为7.5 m,上部结构为(65+110+65)m+3×30 m预应力砼装配T梁+连续刚构,桥长为336.24 m。箱梁为三向预应力混凝土结构,全幅桥采用分离式单箱单室截面。箱顶板宽度为12 m,底板宽为6 m,箱悬臂长为3 m,顶板最小厚度为18 cm,底板跨中厚为32 cm、根部厚为80 cm,腹板厚为50~80 cm。箱梁中线处跨中及边跨现浇梁段高为2.5 m,墩顶0号梁段高为6.5 m,箱梁高度和底板厚度从合拢段中心到悬臂根部按1.8次抛物线变化。
联结墩墩身高为57 m,设计为高桩承台,边跨现浇段底板与原地面高差超过60 m,边跨现浇段长为9 m,悬挑出墩顶长度达到7.2 m。设计合拢顺序为先边跨后中跨,即边跨现浇段需要独立浇筑,现浇段的全部荷载必须全部由过渡墩上或者承台及地面承担。搭设墩旁托架安全风险极大,联结墩渡墩偏心受力不利,施工控制难度极大。搭设落地支架,承担现浇段全部荷载,支架搭设高度超过60 m,国内罕见,安全风险评估难以通过,由于山体陡峭,地基必须进行特殊处理。施工成本极高,施工周期极长,安全风险极大。
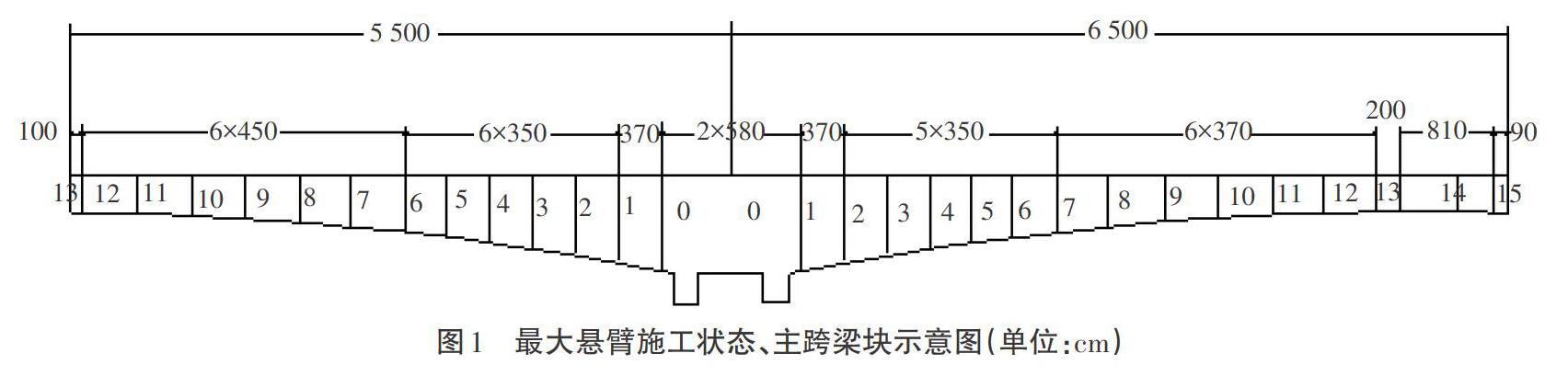
鉴于以上原因,本研究提出不等长连续刚构桥悬臂施工的方案。最大悬臂长分别为55 m和65 m,最大悬臂施工状态的平面图如图1所示。
因悬臂不等长,人们需要考虑配重的位置和大小。在实际施工操作中,配重应尽量靠悬臂前端施加,因为人们要综合考虑加载卸载的方便程度以及必要的作业空间等因素。在横桥向,配重应在横桥向均衡对称施加,这是为了保持梁体横向平衡,保证桥梁不发生侧向倾斜和扭转。配重的大小则与配重施加的位置等因素有关。根据悬臂端下挠变形值相同,配重大小通过计算求得。基本配重大小按等效代换合拢段重量引起的悬臂端下挠效应计算得到。至于附加配重,除需要考虑施加位置外,还需要考虑实际应起的作用和梁体安全。
本文的关键问题在于不等跨梁桥悬臂施工应该采取怎样的措施来解决不等跨梁桥悬臂浇筑施工过程中可能存在的偏载问题。墩的两侧梁段数不同,由图1可以看出,2号墩右侧比左侧多出两个梁块,这种偏载就会产生不平衡的受力。为了消除这种不平衡的受力,短跨侧需要添加压重荷载。
2 有限元建模
本文采用Midas/Civil有限元软件建立了某高架桥主跨的有限元模型,进行曲线和纵坡的建模。荷载有自重荷载及施工荷载。由于模型未建桥墩,所以将支座简化成固定约束,然后将添加支承的两个节点与上方箱梁构建一个刚性连接,本模型针对的是合拢前的施工阶段,桥梁两端不用添加约束。
3 加载方式比选
3.1 水箱加载
在Midas/Civil有限元软件中,将平面荷载添加到图2中41、42、43、44结点围成的矩形中。其中,平面荷载选用均布面荷载,4点围成4 m×5 m的底面积,此平面荷载等效为水箱加载。在荷载工况中添加1号加载形式和2号加载形式,其中,1号加载方式是底面积为2 m×12 m的水箱,2号加载方式是底面积为4 m×5 m的水箱。
3.2 沙袋加载
在图2中38单元、39单元添加单元荷载,使两个单元受压等效为沙袋加载。在荷载工况中添加3号加载形式和4号加载形式,其中,3号加载方式是底面积为12 m×6 m的梁单元加载,4号加载方式是底面积为12 m×3 m的梁单元加载。
上述水箱加载和沙袋加载两种平面加载方式均是预加荷载,下面将通过对比选用更优化的水箱加载形式和沙袋加载形式。
4 结果与分析
4.1 水箱加载
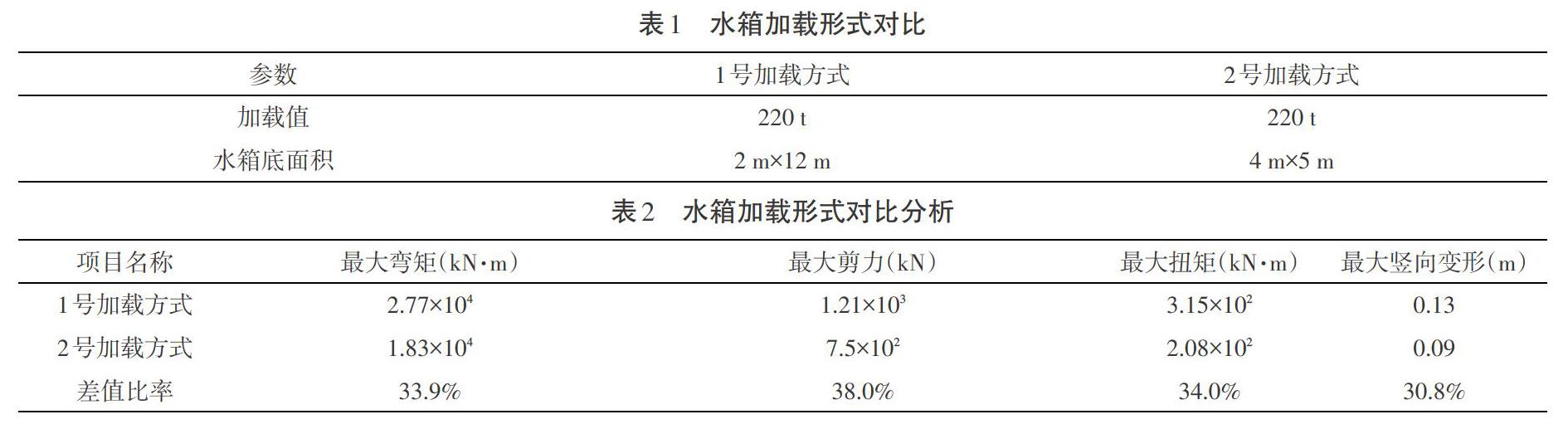
如表1所示,采用两种水箱加载方式进行受力及位移对比分析。利用Midas/Civil有限元軟件,先添加210 t的平面荷载,压载后重新运行分析,再以1 t逐级添加,直到加至220 t,两个悬臂的内力达到平衡状态。两种加载形式所产生的梁单元最大弯矩、最大剪力、最大扭矩、最大纵向变形如表2所示。
由表2可知,在短跨侧进行水箱压载,1号加载方式在最大弯矩、最大剪力、最大扭矩以及梁体竖向位移方面均高于2号加载方式,选用2号加载方式更优。
在施工中,采用水箱加载的压重方式,需要根据上述平面荷载加载位置,在短跨端部砌筑一个5 m×4 m×12 m的水箱,水箱最大加载量为240 t,最终长跨浇筑施工完成的同时,水箱加载到220 t。
4.2 沙袋加载
根据上述沙袋加载方式,利用Midas/Civil有限元软件直接在38单元、39单元上添加单元荷载,考虑更大的接触面积,先添加205 t的压载,得到的弯矩仍旧不平衡,再以1 t逐级递增和递减,最终得到:直到加至203 t,两个悬臂的内力达到平衡状态。这种加载方式采用的是底面积为12 m×6 m的梁单元加载。
同上述加载方式一样,再添加一种底面积为12 m×3 m的梁单元加载,得到的最大弯矩、最大剪力、最大扭矩、最大纵向变形如表3所示。其中,3号加载方式为底面积为12 m×6 m的梁单元加载,4号加载方式为底面积为12 m×3 m的梁单元加载。
从表3数据可以看出,在短跨侧进行沙袋压载后,3号加载方式在最大弯矩、最大剪力、最大扭矩以及梁体竖向位移方面均高于4号加载方式,选用4号加载方式更优。
在施工中,沙袋的加载形式有很多种,现选用由方木和沙袋组成的加载模块,在一个加载模块中,横向和纵向分别依次排列有多条方木形成的方木底座,方木上每隔一定距离设有一个钻孔,在横向方木和纵向方木通过钻孔用螺栓固定,方木底座的上方设有一层沙袋,在模型38单元、39单元梁端上加载,加载底座方木采用5 cm×10 cm×300 cm,采用平均质量为1 t的沙袋,沙袋规格为90 cm×90 cm×90 cm,布载长为3 m,宽为12 m,每层可放置33个沙袋,加载7层,最大布载总量为230 t。
5 结论
基于65 m+110 m+65 m连续刚构桥悬臂不等长施工方案,本研究分别采用水箱加载及沙袋加载方法,对内力及变形进行详细的有限元分析。结果发现,不等长悬臂高架桥有较大的不平衡弯矩,必须在短跨端部添加一定的配重才能达到稳定;若采用水箱加载,则需要在短跨上砌筑一个4 m×5 m×12.5 m的水箱,在长跨浇筑施工完成的同时,水箱加载到220 t时,悬臂两侧受力平衡;若采用沙袋加载,则选用由方木和沙袋组成的加载模块在短跨上加载,加载底座方木采用5 cm×10 cm×300 cm,采用平均质量为1 t的沙袋,布载长为3 m,宽为12 m,7层高,每层放置33个沙袋,沿桥面布置,最终布载203 t。根据上述分析结果,人们对现场施工进行指导,达到了预期效果,说明运用本文的分析方案对连续刚构桥悬臂不等长施工的模拟分析与实际情况是吻合的,完全满足受力及施工控制的要求。
参考文献:
[1]梁曾奇,李因富,黄海东.连续刚构桥长悬臂挂篮施工现浇段、合龙段结构行为分析[J].中外公路,2016(1):192-196.
[2]李定伦.连续刚构桥中跨合拢配重效应分析[J].中外公路,2014(3):131-134.

