一种基于网格的空间聚类算法及在基本农田规划中的应用
吴彦澎


摘要:针对当前基本农田划定过程中主观干预过多的问题,在综合考虑耕地质量情况、交通区位条件和耕地连片性等因素的基础上,提出一种基于网格的基本农田保护规划空间聚类算法。该算法以网格作为分析单元,首先以 K-Means 算法对网格的属性进行初步聚类;然后利用网格间的空间关系和相似性进行最大相似区的确定;最后再以模糊聚类方法对细碎区聚合归并,最终得到基本农田保护区域,可用于指导基本农田保护规划的实施。并通过具体案例分析证明了该算法的可行性和实用性,且具有较高的计算效率。
关键词:基本农田保护;网格;空间聚类;耕地质量;交通区位;连片性
中图分类号:S126
文献标志码:A
文章编号:1002-1302(2020)16-0250-05
耕地入选基本农田就是将总体规划确定的耕地按一定的面积指标有选择地划分为基本农田的过程。目前,在实际划定过程中主观随意性过强,缺乏一定的科学决策,只从经济建设的需求考虑,而忽视耕地的质量要求和耕地连片需求、忽视农田保护的政策规定,使基本农田保护流于形式,不能形成合理优化的空间布局[1]。
鉴于基本农田划定中存在的问题,如何划定基本农田保护区成为学术研究的热点。国内已有学者进行了大量的研究工作,获得了丰富的基本农田划定的理论结果和经验。宇向东等在耕地分等的基础上,将综合评价算法模型移植到基本农田空间配置过程中[2];唐宽金等以粮食生产能力为基础进行了基本农田保护区的划定[3-4];金志丰利用GIS空间分析技术提出依据土地适宜性指数和土地等引入农用地连片性的概念确定了基本农田划定的空间范围[5]。在已有的基本农田划定研究中,主要依据单一的因素进行划定,同时涉及多个因素进行综合分析的研究很少,主要原因是缺乏一种有效的统计单元和综合评价算法。
空间聚类分析可以对耕地地块对象进行聚类,将“属性相似,空间临近”的耕地地块对象划分在同一类别中,即把基本农田的划定看成是基于耕地地块统计单元的空间聚类问题。聚类过程中可以选取多个与基本农田划定相关的因素进行综合评价,同时根据耕地地块之间的空间位置关系进行邻接性调整,以达到优质的耕地连片的效果,最终确定基本农田保护区域。由于空间数据库中耕地数据大多是面状地理实体,最直接的方法就是采用面状数据的聚类算法,而面状数据的聚类过程又存在相似度评价难、不同尺度的面状数据聚类结果必然不同等问题[6-7]。因此,以耕地地块对象作为统计单元进行聚类时,若将不同尺度的因素数据统计到耕地地块中,势必造成无法解释的空间聚类结果。为了弥补统计单元在尺度上存在的不足,本研究采用一种设计稳定、标准化的空间统计单元——网格单元作为统计分析单元,并进而设计了新的聚类算法。
1 基于网格的空间聚类算法实现
陈述彭等从网格地图思想出发,提出建立网格信息系统,用不同精度的网格来划分、存储面状的空间数据及其属性数据[8-10]。用网格作为统计分析单元可以解决耕地地块对象作为统计单元在尺度上的问题。
将面状数据划分成网格后,进行分析时有很大方便,本研究提出的基于网格的空间聚类算法,从网格的数据结构——网格单元出发,统计基本农田划定因素的信息,采用K-Means聚类算法对网格属性进行初步聚类,利用网格单元之间隐藏的空间关系对网格属性聚类结果进行空间邻接性的调整,能够很方便地实现空间聚类。主要过程如下:
1.1 网格的建立
目前,统计数据的获取主要来自于土地利用数据和耕地分等数据,必须依照一定的条件,将现有的土地利用数据和耕地分等数据进行网格划分。本研究综合考虑现有的各种网格划分方法的优劣并结合实际研究的需求,采用基于经纬度坐标的地理网格划分方法[11]。主要步骤如下:
1.1.1 建立地理網格 根据研究区域的最小整经纬度范围、空间对象的尺度进行等经纬度(经纬分)划分。网格大小可根据实际需要的精度确定,例如15″×15″、30″×30″、1′×1′等。
1.1.2 网格属性的获取 地理网格建立后,与土地利用数据、耕地分等数据叠加,获取基本农田划定因素的属性值。部分因素的属性需通过空间计算获取,本研究针对一些基础属性和交通区位条件属性提供了一些统计方法。
基础属性的获取。基础属性包括耕地地块个数、地块面积、平均地块分维数等。针对地块个数,首先构建每个耕地地块的最小外接矩形;其次计算最小外接矩形的中心点坐标及落入的网格编号;最后统计每个网格中落入的中心点个数,即为网格中耕地地块的数量。其他基础属性可根据各指标的计算公式进行获取。
通达度属性的获取。通达度属性是指耕地到主干线、城镇、村庄的距离。在当前计算的耕地地块所在的网格内可能不存在主干线等地物,本研究针对此情况采用8邻域迭代检索的方法获取邻接网格内主干线等地物,并计算与其最短距离(图1)。以主干线通达度计算为例,高亮显示的耕地地块所在的网格0中不存在主干线地物,因此需要在网格0周边8个方向的网格内寻找。检索到网格6、7、8存在主干线地物,当前计算的耕地地块分别同3个网格内的主干线进行距离计算,选取最小距离进行存储。若网格0的8邻域网格内都不存在主干线地物,则向外扩展检索范围,直至寻找到为止。
1.2 网格聚类步骤描述
本研究采用基于密度思想的K-Means算法作为基础算法对网格属性进行聚类[12-13],通过相似网格的扩张得到空间聚类结果,这种方法能够充分利用网格的数据结构。算法主要分为4个步骤:
1.2.1 确定K-Means算法的初始聚类中心 考虑到聚类结果受随机选取的初始聚类中心的影响,本研究采用基于网格密度的初始聚类中心选取方法,确定最优的初始聚类中心。网格密度为属性中统计的耕地地块的个数,个数越多,网格密度越大。
1.2.2 属性聚类 地理网格建立后,每个网格单元就是一个待分类对象,对所选属性进行归一化处理。根据步骤1确定的初始聚类中心,应用 K-Means 算法进行属性聚类,得到每一个网格的聚类类别。该步骤完成“属性相似”的聚类过程。
1.2.3 最大相似区和核心区的确定 对网格数据进行线性扫描,获取当前处理的网格聚类类别并判断8邻域内的网格单元是否相似(即类别是否相同),若存在相似的网格单元则进行扩张获取更多相似网格单元形成最大相似区。设定最大相似区域网格数阈值θ,将小于阈值θ的最大相似区标记为“临时噪声区”,大于阈值θ的最大相似区标记为核心区。
1.2.4 “临时噪声区”的处理 遍历步骤3中的“临时噪声区”,判断每个“临时噪声区”内的网格是否为无效网格,若是,则标记为噪声区;若否,同邻接的核心区进行相似度计算,合并到相似度最大的核心区中。该过程中的无效网格是指网格区域范围内无耕地存在的网格。
1.3 网格聚类算法过程
输入参数:网格划分步长λ,K-Means聚类数目k,最大相似区网格数阈值θ。
1.3.1 建立地理网格 第一步,根据输入网格划分步长λ建立地理网格。
第三步,依次遍历所有网格,重复第二步。
第四步,对网格属性set={I1,I2,…,Im}进行归一化处理,形成网格单元聚类维度属性set′={I1′,I2′,…,Im′}。
1.3.2 基于密度的K均值聚类 第一步,从网格属性集set′中获取网格密度,将密度最大的网格单元G[i]作为第一个初始聚类中心,存入初始聚类中心集合C。从set′中寻找下一个密度最大网格,该网格到C的欧氏距离最远。当C中网格个数等于k时结束。
第二步,引用K-Means算法对参与聚类的因素属性进行聚类,得到每个网格单元的属性聚类结果ClassID。聚类过程中采用加权的欧氏距离作为相似度判断的依据。
1.3.3 最大相似区域获取 第一步,所有网格单元初始遍历标志Visit=false,最终聚类结果FinalID=0,最大相似区AreaID=0。
第二步,创建一个队GridArray,存放邻域网格ID。
第三步,从G[0]开始对所有网格进行线性扫描,检索访问标识Visist=false的网格单元G[i],获取其8邻域内网格单元集,设定该网格遍历标志Visit(G[i])=true,最终聚类结果FinalID(G[i])=ClassID(G[i]),相似区AreaID(G[i])=1。若8邻域网格单元集中存在遍历标志Visist=false且FinalID(G[i])=ClassID的网格单元,将该网格ID加入GridArray。若不存在,访问下一个遍历标志Visist=false的网格单元。
第四步,当GridArray不为空时,读取队头网格,转下一步。当GridArray为空时,重复第三步,AreaID加1。
第五步,取队头网格,设其遍历标志Visist=true,FinalID=FinalID(G[i]),AreaID=AreaID(G[i])删除队头网格,重复Step3。
第六步,最大相似区获取结束。
1.3.4 “临时噪声网格区”的处理 第一步,统计每个最大相似区内网格个数Count。若Count>θ,则该最大相似区标记为核心区;若Count<θ,暂时标记该相似区为“临时噪声区”。
第二步,若“临时噪声区”内网格单元为无效网格单元,则标记为“噪声区”。否则将“临时噪声区”同邻接的核心区做相似度计算,合并到相似度最大的核心区。相似度采用加权的欧氏距离作为判断的依据
第三步,处理结束,将核心区结果作为最终聚类结果。
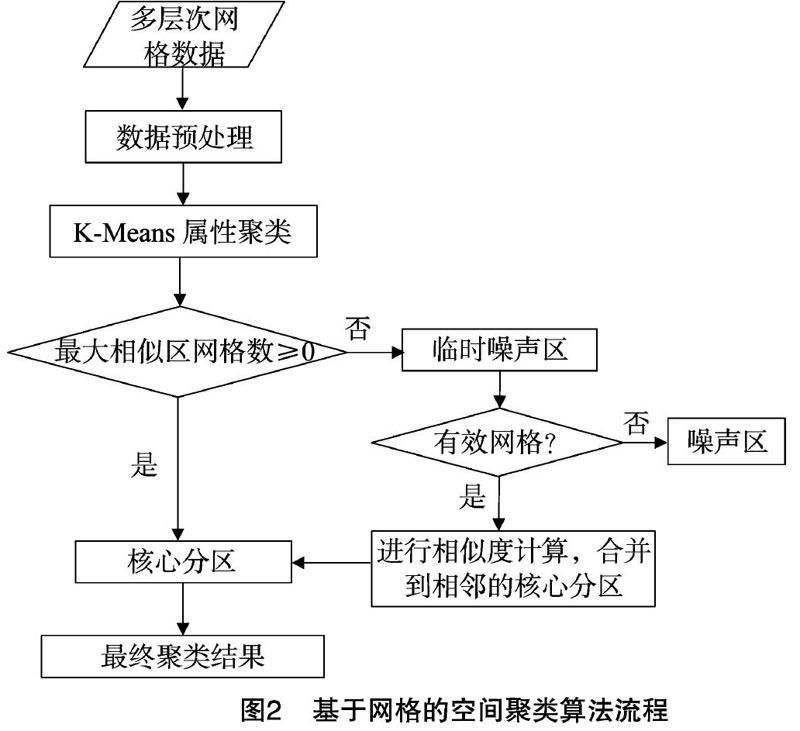
具体算法流程见图2。
2 应用案例分析
2.1 应用区现状与数据源
选择江苏省宝应县为研究区,宝应县地处江苏省中部,京杭运河纵贯南北,县域东西长55.7 km,南北宽47.4 km,全境总面积1 467.4 km2。該县属黄淮冲击平原,分成东西2部分,西高东低;沿运河两岸高亢,东西边缘低洼;运东南北两侧略高,中间偏低。
本研究以2008年全国第二次土地调查的 1 ∶ 5 000 宝应县土地利用现状数据作为基本分析图件,以1 ∶ 25万宝应县耕地分等数据、宝应县土地
利用总体规划(2006—2020年)数据作为辅助分析资料。
2.2 结果与分析
依据高标准农田、农田保护的概念及内涵以及基本农田保护区规划的影响因素,在确定基本农田划分区域时应首先考虑耕地的质量水平、耕地地块所处区域的区位交通条件,优先将利用程度高,耕作便利的耕地优先确定为保护网格;还应考虑耕地的集中连片条件、土地利用结构等因素。本案例最终确定宝应县基本农田划定指标和权重见表1。
(1)本研究网格采用经纬差30″为网格间距,生成网格数=24×33的图层,其中有效网格数为536。网格属性的获取主要来自宝应县土地利用现状数据,土地利用现状数据中道路、城镇、村庄图斑参与通达度计算,耕地质量等级指标利用耕地分等数据获取。宝应县建立后的地理网格和基本数据情况见图3。
(2)设定K-Means算法的聚类数目k=3,在阈值参数θ=4的水平下,得到33个最大相似区,其中细碎区占50%以上,但细碎区网格个数仅占总网格的5.03%。这些分区的具体统计信息见表2。
(3)细碎区的处理。根据“1.2”节中针对细碎区的处理流程对细碎区进行合并,最终得到9个核心区。属性聚类结果和细碎区调整后的最终聚类结果见图4。为了清晰起见,给出了每个类别调整前后的统计信息(表3)。
本案例对3个类别中参与聚类的网格属性进行统计分析,最终划定第一类网格区域作为宝应县基本农田保护区,主要集中在宝应西北部、东部和南部地区。与宝应现行基本农田保护规划对比,宝应县东北部的基本农田保护区与规划不一致,分析认为,该地区耕地面积比例较低、连片性差,且自然等级相对较低,因此不适宜作为耕地保护区。宝应县南部耕地面积集中,耕地连片性指数、耕地的自然等和利用等指数相对较高,因此适宜作为基本农田加以保护。由于案例中聚类算法得到的基本农田保护区考虑的因素同规划有所差别,虽能确定耕地保护区的空间位置,但并不能同规划区域完全一致。总体来说,利用本研究的空间聚类算法进行基本农田保护区的划定能够指导基本农田保护规划的实施。
3 结论与讨论
以网格作为统计单元,可以获取不同尺度的耕地入选基本农田的指标信息,进行多因素综合分析。同时可以利用网格间的空间位置关系完成空间聚类,确定基本农田保护区域。在全面考虑基本农田划定影响因素的基础上,以江苏省宝应县基本农田划定为例,验证了算法的可行性和实用性。算法只需对网格进行1次线性扫描即可完成整个聚类过程,具有较高的效率。
科学地划定基本农田并非一个简单随意的过程,它需要综合考虑多方面的因素,既包括耕地自身的条件,如质量状况、区位条件等,还包括人为因素的影响,如行政干预、政策限制等,而这些因素之间又相互影响、相互交叉,有时甚至相互矛盾、相互冲突。因此,本研究空间聚类算法的应用必须经过一个综合分析、评价和判断的过程,才能作出科学的决策。
参考文献:
[1]展瑰琦,郑伟元. 关于基本农田保护区规划与划定的几个问题[J]. 中国土地科学,1997,11(1):12-14.
[2]宇向东,郝晋岷,鲍文东. 基于耕地分等的基本农田空间配置的方法[J]. 農业工程学报,2008,24(增刊1):185-189.
[3]唐宽金,郑新奇,姚金明,等. 基于粮食生产能力的基本农田保护区规划方法研究[J]. 地域研究与开发,2008,27(6):105-109.
[4]金志丰. 基于GIS空间分析的基本农田配置研究[J]. 水土保持通报,2010,30(5):134-137,164.
[5]周尚意,朱阿兴,邱维理,等. 基于GIS的农用地连片性分析及其在基本农田保护规划中的应用[J]. 农业工程学报,2008,24(7):72-77,封3.
[6]杨 帆,米 红. 一种基于网格的空间聚类方法在区域划分中的应用[J]. 测绘科学,2007,32(增刊1):66-69.
[7]吴信才,刘少雄. 基于邻接关系的空间数据挖掘[J]. 计算机工程,2002,28(7):89-91.
[8]陈述彭,陈秋晓,周成虎. 网格地图与网格计算[J]. 测绘科学,2002,27(4):1-6.
[9]周成虎,欧 阳,马 廷. 地理格网模型研究进展[J]. 地理科学进展,2009,28(5):657-662.
[10]陈述彭,周成虎,陈秋晓. 格网地图的新一代[J]. 测绘科学,2004,29(4):1-4.
[11]国家质量监督检验检疫总局,国家标准化管理委员会. 地理格网:GB/T 12409—2009[S]. 北京:中国标准出版社,2009.
[12]刘智杭,于 鸣,任洪娥. 基于改进K均值聚类的葡萄果穗图像分割[J]. 江苏农业科学,2018,46(24):239-244.
[13]Arthur D,Vassilvitskii S . K-Means+ +:the advantages of careful seeding[C]. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms,New Orleans,2007.

