基于混合测量模式的压缩感知研究

杨云仙,梁卫文

(深圳技师学院 信息与通信学院，广东 深圳，518000)

压缩感知理论自从2006年问世以来[1，2]，引起了全世界学者的极大关注。其打破了传统的对模拟信号幅值进行等间隔逐点采样的方法，将对信号的采样变成了对信息的采样，突破了奈奎斯特采样定理所要求的最低采样频率下界，使得人们可以用极低的采样频率对模拟信号进行采样。并且，压缩感知理论表明，当信号具有K稀疏性时，原信号可以通过测量值以高概率精确恢复。该理论的出现无论对于理论研究还是实践应用都具有极大的吸引力。例如，对于目前常用的数码相机，像素值动辄达到上千兆，然而实际更多使用的是经过JPEG压缩之后的图片。这种对模拟信号进行过采样，再使用压缩算法进行压缩以丢弃冗余采样点的采样方式极大地浪费了硬件及软件资源，为信号的存储、传输带来极大的不便。

压缩感知理论的出现，为上述问题的解决提供了一条有效的途径。然而，对于自然世界中的信号而言，一般是不满足稀疏性这个压缩感知理论应用的大前提的，若原始信号不稀疏或在某一正交基下也不稀疏，则利用压缩感知理论对信号进行测量后恢复出来的信号与原信号误差较大，这使得压缩感知理论的应用受到了极大的限制。对于此，文献[3]、[4]针对信号的稀疏表示提出了一些解决算法，从而提升压缩感知算法的恢复效果。另外，文献[5]中根据小波变换高频系数和低频稀疏的特性提出了基于单层小波变换的压缩感知算法，较大地提升了压缩感知对图像的恢复质量。本文在文献[5]的基础上，进一步将基于单层小波变换的压缩感知算法改进为混合模式的压缩感知算法，使得算法具有更好的灵活性及实用性。最后，还将对小波分解层次、测量值数量的选取进行详尽的实验分析，为进一步的工程实践应用提供可靠的依据。

1 压缩感知理论简介

设x∈R×1为一维信号，ψ={ψ1,…,ψN}为一组正交基，则x可由ψ线性表出，即

(1)

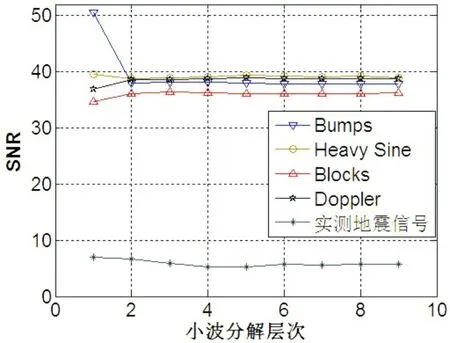
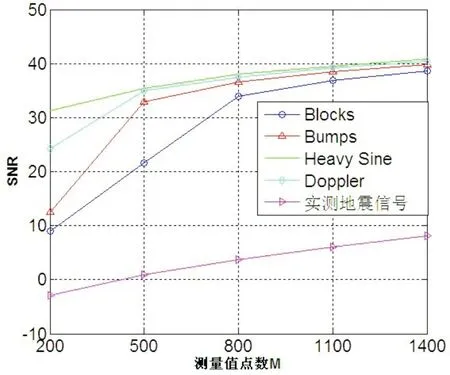
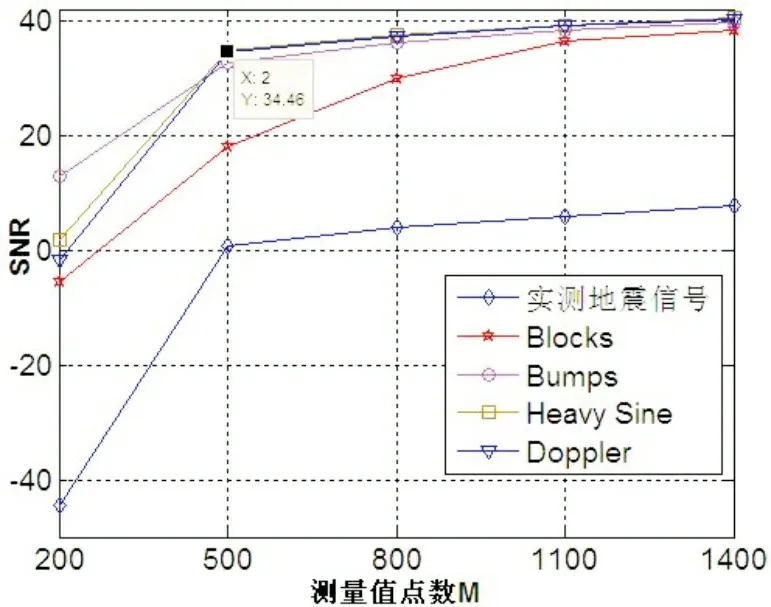
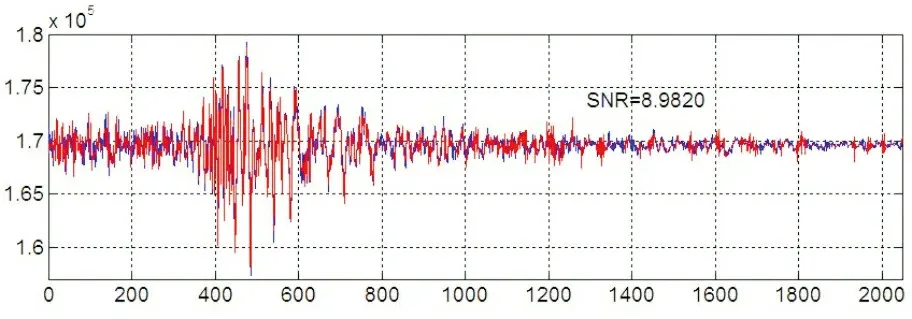
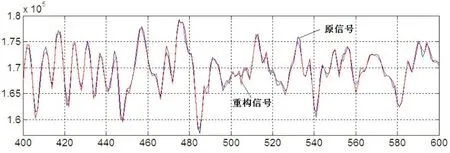
其中αk=

由(1)式可知，若信号不稀疏，其经过正交变换后，可以得到稀疏的系数，这即满足了压缩感知理论所需的前提，我们可以利用测量矩阵对稀疏系数进行测量，得到测量值(采样值)，然后对测量值进行熵编码以便于数据的存储及传输。在解码时，只需对编码值进行熵解码，然后根据压缩感知的理论，利用凸优化算法即可得到系数的稀疏逼近，再利用正交逆变换重构原信号。设Φ={φ1，…，φN}为一M×N，M▯N的测量矩阵，则对于稀疏的系数进行测量可得到M个测量值，即：

y=φα=φψHX

(2)

由此可以看到，压缩感知将N维信号x降维为M维信号y。由于式(2)中未知数的个数N大于方程个数M，因此若直接求解式(2)来重构信号x不能得到确切解。但系数α是K稀疏的，即至多有K个非零系数，且K

min‖α‖l0,s.t.φα=y

(3)

而l0范数的求解是个NP-hard问题，因此可以将问题转换为[10]：

min‖α‖l1,s.t.φα=y

(4)

对于式(4)中l1最小范数下的最优化问题，目前的求解算法有匹配追踪法[6]、正交匹配追踪法(OMP)[7]，梯度投影法(GP)[8]、链式追踪法[9]等。

2 基于混合测量模式的压缩感知算法

在文献[5]中，由于图像进行小波变换后，低频系数不稀疏，高频系数稀疏，若对全部的低频和高频系数利用测量矩阵Φ一起进行测量，则由于低频稀疏的不稀疏性会导致压缩感知重构效果较差，因此需要尽可能增大对图像的小波变换层数。这一方面带来了运算量的增大，另一方面，即使是使用了最大的小波分解层数，压缩感知重构的图像质量也不能满足实际的需要。由于低频系数是原图像的逼近，其在小波重构中具有重要的作用，因此[5]中仅对图像进行一层小波变换，且仅对高频小波系数进行测量，而保持低频系数不变，从而提升图像重构质量。这便存在一个问题，即该方法会极大地限制了压缩感知算法对高维信号的降维作用，例如，对于一个256×256的图像，其经过一层小波变换后，得到{LH1, HL1, HH1, LL1}四个小波子带系数，LL1为低频子带，其大小为64×64，因此，测量值M必然要满足M>64×64，即对原图像的压缩率至多为1/4。若对于一维信号采用此方法，则压缩率至多为1/2。因此，在本文中，将单层小波分解进一步拓展为多层小波分解，结合文献[6]中保留低频系数的思想，使得测量值M的选取具有更大的灵活性，在保证一定的信号重构质量的同时进一步增大压缩率。

我们改进的混合模式的压缩感知算法思想为：首先对原信号进行J层小波变换，得到各层高频系数及第J层低频系数{aJ,dJ,dJ-1,…,d1}，其中aJ为第J层低频系数，dj，1≤j≤J为j第层高频系数。由于低频子带系数对于信号的小波重构起到了很重要的作用，因此对低频子带系数不进行测量，以避免由于压缩感知算法而带来的误差；对于{dJ,dJ-1,…,d1}，利用测量矩阵进行测量。这样对低频不测量仅对各层高频进行测量的混合测量模式能进一步增大压缩感知算法对信号的压缩率，且由于保持了低频系数不变，与经典的压缩感知算法相比，重构信号质量也能得到有效提升。对一维信号而言，算法具体实现步骤如下：

步骤1， 对N(N=2L)点信号x进行J层小波变换，得到各层高频系数及第J层低频系数{aJ,dJ,dJ-1,…,d1}，则aJ有2L-J个低频系数点，各层高频系数共有N-2L-J个系数点。

步骤2，选择合适的M值，构造M×N-2L-J大小的服从(0,1/N)高斯分布的测量矩阵Φ对{dJ,dJ-1,…,d1}进行测量，得到M×1的测量值向量y。低频子aJ带系数则保持不变。

3 仿真结果

从图1可以看出，当小波分解层次大于等于2层以后，本文算法对各个信号的重构质量基本相同，但是这样可以使得测量值M取小于原信号长度的一半以下，增大了压缩感知算法对信号的压缩率。通常，小波分解层次取为4～6层即可。图2给出了当小波分解层次为5层时，随着测量值M的增大，各个信号重构的SNR图，小波函数同样使用sym8小波。此处为了叙述方便，对于本文提出的基于混合测量模式的压缩感知算法而言，M值指的是原信号经过J层小波分解后第J层低频系数个数及对各层高频系数测量值个数之和。图1和图2中明显看出，由于实测地震信号非常复杂，其经过小波变换后稀疏度较差，重构信号的质量较差。

图1 不同信号在不同小波分解层次下使用本文算法得到的重构信号SNR，M=1024

图2 不同信号在不同测量值点数下使用本文算法得到的重构信号SNR

图3 不同信号在不同小波分解层次下使用经典压缩感知法得到的重构信号SNR，M=1024

图4 不同信号在不同测量值点数下使用经典压感知算法得到的重构信号SNR

为了便于比较，我们还给出了经典基于小波变换的压缩感知算法对此5种信号的仿真比较图。在经典的压缩感知算法中，对原信号进行J层小波分解，然后对包括低频系数在内的所有小波系数利用测量矩阵进行测量，得到M个测量值点，最后再利用凸优化算法恢复。其中小波函数仍然选用sym8小波，图3给出了不同的小波分解层次下各个信号的重构SNR，其中测量值点数为1024点。可以看出，当分解层次大于等于4层以后，重构信号SNR基本保持不变。当分解层次为5层时，在不同的测量值点数下，5个信号的重构信号SNR如图4所示。

比较图1和图3可以看出，当小波分解层次大于等于5层之后，本文算法与经典的压缩感知算法重构信号质量差别不大，这是因为对于2048个点的原信号，若进行5层分解，则第5层的低频系数只有64个，而5层高频系数共有1984个点，低频系数个数已经远小于高频系数个数，因此本文算法中保留低频系数的方法不会对SNR有很大的提高。但是在分解层次小于等于4层时，由图1和3可以看到，本文算法重构信号质量与经典压缩感知算法相比有很大的提高。

对于图2和图4，可以看到，当测量值点数M较小时，例如M<500时，由于本文算法保留了低频系数，对于重构信号起到了很重要的作用，避免了由于随机矩阵测量和凸优化算法带来的重构误差，因此重构信号质量大大优于经典压缩感知算法。当M值较大时，使用经典压缩感知算法也能较好的获取原信号的信息，因此信号重构质量与本文算法相当。

图4给出了在地震信号在小波分解层次为3层、M=1400情况下重构的地震信号与原始信号的比较图。图5给出了同样条件下doppler信号的时域比较图，可以看出，对于doppler信号，已经几乎完全恢复了原信号。

(a)利用本文算法对实测地震信号重构结果

(b) 图3(a)中400～600点放大图

图6 利用本文算法对Doppler信号重构结果与原信号比较

4 结语

本文提出了基于混合测量模式的压缩感知算法，利用本文算法，可以克服文献[5]中对于测量值点数的限制，使得算法更具有实用性。并且，将经典的压缩感知算法结合[5]中保留低频系数的思想，得到了本文提出的混合测量模式，即对最大低频层系数保持不变，只对各层高频系数进行测量，从而提高压缩感知算法的压缩比及重构质量。最后对算法进行了详细的仿真，仿真结果表明本文算法可以较好地对信号进行压缩采样，且能获得较好的信号恢复质量。