台风影响期间文昌航天发射场浅层风预报技术研究

贵志成 王艳莹 赵小平 甘思旧

（1 63796部队，西昌 615000；2 民航海南空管分局，海口 570100）

0 引言

浅层风是近地面层中的风，近地面层是大气边界层最接近地表面的部分，约为距离地表10～100 m的大气。航天发射任务中，火箭在垂直转运和加注发射阶段，遇到强浅层风天气，可能会影响航天发射任务成败，因此浅层风预报一直是航天气象保障的重点。热带气旋是最具破坏力的自然灾害之一[1]，文昌航天发射场（以下简称场区）位于海南岛东北海岸，年平均受到3.58个热带气旋影响，大多数台风都是从东南方向移近海南岛，海南岛东部海岸受台风影响最严重，受到台风影响时间也较长[2]。而出现强浅层风天气个例中，热带气旋造成的浅层风风速大、大风影响时间长、风速变化规律较复杂。夏秋季场区频繁受到台风影响，受台风影响时浅层风变化特征一直是浅层风预报研究的重点和难点。日常浅层风预报保障中，台风影响文昌场区时浅层风风速的定量化研究较不足，台风开始影响的具体时间也较难把握，如2016年台风莎莉嘉登陆万宁时，24 h风速预报最大偏差为14.5 m/s。场区受台风影响时，浅层风强风是造成设备设施的损坏、危害人员安全的主要因素，提高浅层风预报准确率可以为航天发射任务气象保障提供支撑。

目前对台风机理研究和台风引发区域大风研究的主要方法是基于动力学的数值模拟分析[3-5]。孙学金等[6]利用WRF-LES模式对大气边界层内大尺度湍涡进行解析，提高了干旱湖区近地面风场数值模拟的真实性和准确性。冯慧敏等[7]利用数值预报资料进行郑州市地面风的多模式预报试验，发现在数值预报的基础上，通过统计降尺度预报能进一步提高地面风预报准确率。

对基层气象预报员来说，统计学方法在计算效率和应用层面上较数值模式更具优势，在数据趋势描述方面，线性回归具有直观性和简洁性。黄奕武等[8]利用T639数据线性回归方法，建立了台风中心预报误差与环境风整层垂直切变的24～120 h线性预估模型，且预估模型有较好的预估效果。农吉夫[9]也通过条件数分析方法，建立了西北太平洋台风强度多元回归模型。科研单位主要研究重点为台风发生发展机理和台风结构分析，地方业务单位主要进行地面风预报，对浅层风的预报技术研究较少。风力发电站有浅层风精确预报的需求，但是大多是向气象公司寻求商业服务，利用统计学方法进行台风影响时浅层风特征及其预报技术的研究相对较少，本文针对业务工作中的实际需求，以提高预报准确率为目的，通过统计分析的方法研究台风影响场区时浅层风预报偏差的影响因子，进行因子设计试验，建立受台风影响时场区浅层风24 h预报回归方程。

1 数据来源及统计范围

浅层风实况数据是架设在文昌场区内的三个浅层风测风塔探测2015—2017年50 m高度10 min平均风向风速。资料统计范围为2015年6月—2017年10月影响场区的9个台风个例。

场区浅层风受台风影响日的定义：

1）台风开始影响日：浅层风风速比上一日平均风速增大4 m/s或以上。

2）台风影响结束日：当日浅层风平均风速比前一日浅层风平均风速减小4 m/s且最大风速小于10 m/s，则前一日为台风影响结束日。

2 浅层风预报偏差分析

2.1 预报概况

场区24 h浅层风预报共分为四段，分别为18：00—24：00、00：00—06：00、06：00—12：00、12：00—18：00。预报每个时段50 m高度最大风速和最大风对应风向。根据台风影响场区的定义，共筛选出受台风影响日数26 d，每天数据分为4段，共整理了台风影响场区共26 d（104段）实况和预报数据。26 d浅层风24 h预报准确率为67 %，离浅层风精准精细预报的要求还有一定差距。

2.2 预报偏差的过程能力分析

台风影响期间，由于浅层风风速较大，风向变化相对连续[10]，浅层风风向预报准确率高，按照风向的评分标准基本不会出现风向预报错误的情况，因此本文主要对风速预报偏差进行分析。

通过正态检验发现，浅层风预报偏差服从正态分布，且各数据间相互独立，可以进行过程能力分析。过程能力指数反映过程在受控状态下时，客户要求与过程表现（产品质量或服务质量的变动程度）的比值，如果过程表现越能满足顾客要求，则过程能力指数值越大[11]。

根据浅层风预报评定标准，设定目标为浅层风预报准确率大于80 %，假设24 h 4段浅层风预报和实况风速偏差均小于等于3 m/s时，预报准确率为84 %（在风向全部正确的情况下），满足目标要求。因此将上下限规定为±3 m/s，即USL=3 m/s，LSL=−3 m/s。

通过计算得到各段浅层风预报偏差的能力直方图（图1），其中，Cp值反映过程的潜在能力，Cp值越大，则过程受控程度越高，Cpk反映过程的实际表现，能反映出工序偏离规格中心的问题，Cpk值越大，则过程偏移量越小。

浅层风预报平均绝对偏差为3.46 m/s，预报偏差组内标准差为4.72，平均偏差Cp值为0.21，Cpk值为0.13，4段浅层风预报偏差都存在正偏倚情况，即实况风速大于预报风速出现次数较多。

3 台风关键因子的识别

从台风特点出发，考虑台风强度、台风相对场区位置和台风与场区距离三个影响因素与预报偏差的关系[12]，通过统计发现，台风与场区距离对预报偏差有正相关关系，即台风距离场区越近，越容易出现预报偏差。接下来将对台风强度、台风相对场区位置两个要素与预报偏差的关系进行分析。

3.1 台风强度与预报偏差的分析

从影响场区浅层风台风强度对预报偏差的卡方检验来看（图2），热带风暴级出现的频数最高，且对预报偏差的贡献率最大，其次为强热带风暴级影响场区时容易出现浅层风预报偏差。热带低压级虽然出现频数第二，但是对预报偏差的贡献率较小，即热带低压影响场区时浅层风预报偏差较小。总的来说不同强度台风对预报偏差有显著差异，但二者并不是呈正/负相关关系。

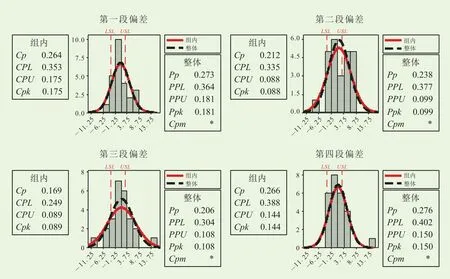
图1 浅层风预报偏差的过程能力分析Fig. 1 Analysis of process forecast capability based on shallow layer wind forecast deviations

3.2 台风方位与预报偏差的分析

影响海南岛台风生成源地为南海和西太平洋，台风主要从海上向西或西北方向移动影响场区[13]，不同方位的台风对场区浅层风的影响有一定差别，为了将不同方向移近并影响场区的台风进行区分，对受台风影响时浅层风风向进行划分，将水平方向风向划分为八个象限，角度分别为（0°≤第一象限＜45°、45°≤第二象限＜90°、90°≤第三象限＜135°、135°≤第四象限＜180°、180°≤第五象限＜225°、225°≤第六象限＜270°、270°≤第七象限＜315°、315°≤第八象限＜360°），按照八个象限对浅层风风向进行划分，不同的象限反映出台风相对于场区的方位。通过统计风向和预报偏差的卡方拟合度检验（图3），发现场区受到台风影响的风向主要在第一至第六象限，未出现第七、第八象限风向。场区浅层风风向为七、八象限时，台风位于场区西北方向，很有可能已经登陆大陆地区，台风登陆后强度减弱明显，大风区影响范围也显著减小，因此对场区影响也不明显。从图中分析可以发现，风向为第一、第三象限时对浅层风偏差贡献率最大，且出现频率也较高，第六象限卡方值的贡献较大，但主要为负贡献。台风影响场区时，南风（包括西南风、南风、东南风）比北风（包括西北风、北风、东北风）出现偏差的可能性更高，浅层风为北风时台风位于场区东侧海上，浅层风为南风时，台风位于场区西侧，很有可能已经登陆海南岛，因此台风中心距离场区位置相对于北风时更近，风速变化幅度更大，所以也更容易出现浅层风预报偏差。

4 台风影响时浅层风预报方程建立与检验

图3 影响场区浅层风预报偏差和风向的卡方拟合度检验Fig. 3 The goodness of Chi-Square fitting test between shallow wind forecast deviation and typhoon wind direction

台风的预报主要依靠数值预报模式，数值预报模式对未来24 h内台风强度的预报准确率可达80 %左右[14]，24 h内台风路径预报的偏差不超过100 km。浅层风预报中主要参考场区附近数值预报低层风速，在研究中发现，建立回归方程时选取925 hPa高度风场作为回归方程自变量有较好的显著性。因此在建立回归方程时考虑四个自变量，分别为925 hPa数值预报风速、台风强度、台风象限、台风相对场区距离。

由于数值预报产品中925 hPa高度风场分辨率为0.25°×0.25°，场区位置没有处于数值预报网格点中，因此选取场区周围4个网格点进行数据分析（图4），4个点的经纬度分别为场区左上（19.75°N，110.75°E）、左下（19.50°N，110.75°E）、右上（19.75°N，111.00°E）、右下（19.50°N，111.00°E），下文分别以a、b、c、d代表4个网格点，对4点数据进行单因子试验设计。

4.1 数值预报风速的单因子检验

分别对选取的4点数据进行一天4段的相关性分析（表1），从表中可以看到，a、b、c、d点和四点平均与实况的相关系数均在0.6以上，且均通过水平为95 %的可信度检验，纵向来看，数值预报与第一段实况的相关系数最大为0.81，与第四段实况的相关系数最小为0.68，相关系数由第一段实况向第四段实况逐渐递减。横向比较a、b、c、d点和四点平均与实况的相关系数，发现各点之间相关系数差异较小，a点和四点平均与实况的相关系数略大。

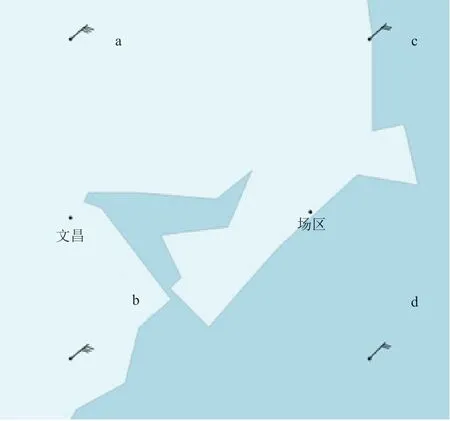
图4 场区位置及网格点的选取Fig. 4 Location of the site and grid selection

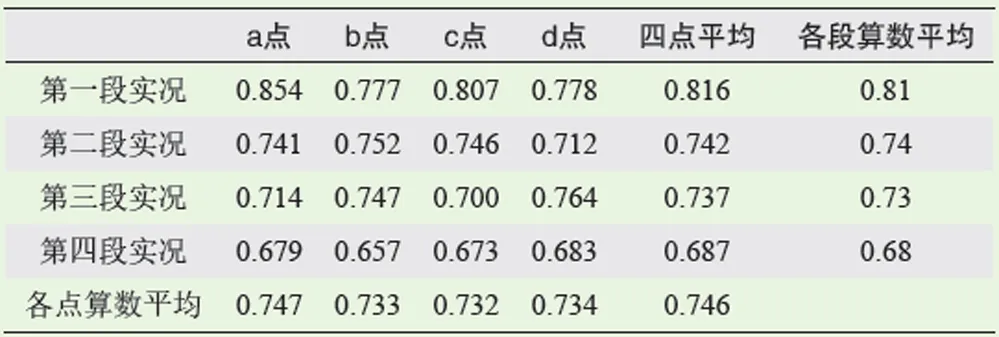
表1 数值预报与实况序列的相关系数Table 1 Correlation coefficient between numerical prediction and observed data

分析各点数据与实况风速偏差的基本统计量（表2），可以看到，b点的平均偏差值最小，四点平均偏差数据的标准差、标准误差最小。综合考虑相关系数与基本统计量结果，选取相关系数最大，且偏差的标准差、标准误差最小的四点平均数据作为拟合方程中的基本数据。

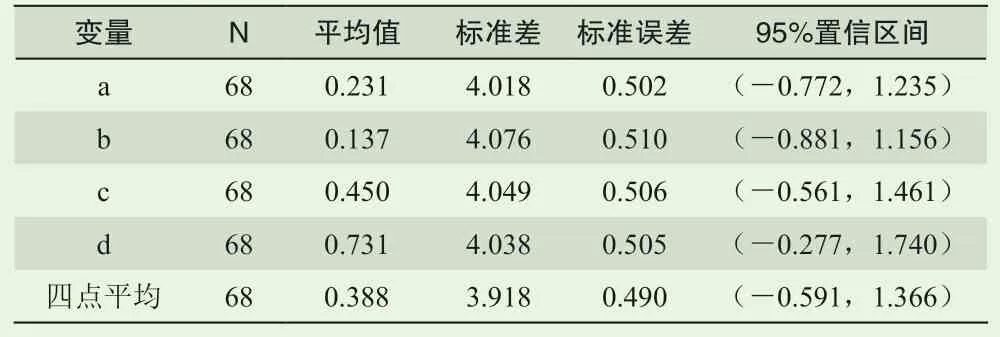
表2 各点数值预报值与实况偏差的基本统计量 Table 2 Basic statistics of numerical prediction and observed data deviation in different grids

通过相关性检验可以发现，数值预报风速与实况风速有很高的相关性，而台风强度、台风方位、台风距离与实况风速的相关性均不超过±0.3，因此在因子设计中主要分析这三个要因与实况风速的检验。

4.2 因子设计分析

为了确定因子对响应变量的影响，确定关键因素的适当设置以取得响应变量的变异最小化。对925 hPa数值预报风速、台风强度、台风方位（象限）、台风与场区距离四个因子进行因子设计。考虑到进行因子设计、选定回归模型后要进行模型效果检验，因此在进行因子分析时选取2015—2016年场区受台风影响的17 d×4段共68段数据，在模型效果检验阶段选择2017年5次台风的9 d×4段共36段数据进行效果检验。

因子设计阶段共设计三组对照试验（表3），通过因子逐步剔除的方法，将回归方程中不显著项剔除，方程中自变量能通过显著性检验，则方程的稳定性较高，因此试验1至试验3的因子数量逐渐减少。在建立回归方程过程中，首先考虑回归方程的稳定性，其次考虑回归方程拟合度。

对比三组试验回归效果（表4），其中S为残差的标准差，R-Sq为回归模型误差占总误差的百分比，取值范围为0～100%，数值越大，表明回归模型数据温和越好。R-Sq（调整）为调整后的R-Sq，与R-Sq数值越接近，表明回归模型越可靠。各试验间S、R-Sq和R-Sq（调整）差距不大，但从因子的显著性来看，试验3中各因子都能通过显著性检验，而且在回归效果差距不大的情况下，选择更少的因子可以节约计算量。

表3 试验设计及各试验回归方程Table 3 Tests designs and the regression equations

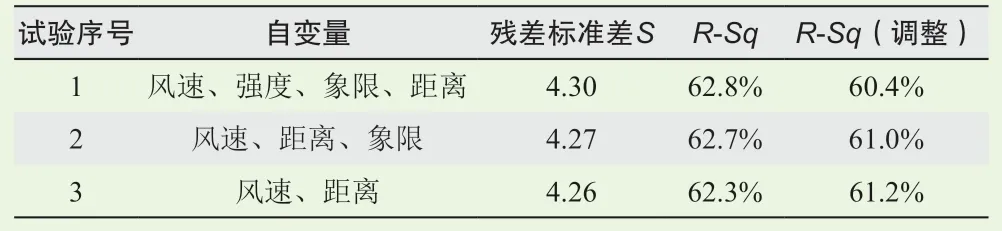
表4 各试验效果对比Table 4 Comparison of test results

4.3 试验3可靠性分析

通过逐步剔除法找到试验3为最理想回归方程，对试验3回归方程的可靠性进行分析，回归方程的显著性检验P值为0.0，可以通过可信度为99 %的显著性检验。从回归方程的残差图中可以看到（图5），图5a为残差正态性概率图，累计的概率点列沿对角线分布，则说明残差服从正态分布，且概率点越接近对角线分布，说明回归效果越好。图5b为响应变量对应的残差图，残差点在横轴上下随机波动，即不存在某种连续性的波动趋势。图5c为残差的正态分布图，可以看到残差分布集中的区域为−4～4。图5d为按观测值顺序的残差分布，残差分布为随机波动。通过对残差图的分析，认为试验3回归方程（Y=12.2+0.523×风速−0.0133×距离）稳定性较好，且方程结果不发散，是逐步剔除试验中的最优选择。

4.4 回归方程效果检验

将2017年9d 36段风速数据代入试验3回归方程Y=12.2+0.523×风速−0.0133×距离，算出预报风速后与实况对比，对偏差进行过程能力分析（图6），偏差的组内标准差为3.74，整体标准差为3.68，Cp值为0.27，Cpk值为0.19。

将试验3的回归验证结果与浅层风预报偏差的过程能力分析进行对比（表5），回归方程得到预报风速有8次偏差大于等于4 m/s。改进前预报偏差有12次风速大于等于4 m/s。建立回归方程后得到的回归风速标准差比改进前减小21 %，Cp值提高28 %，Cpk值提高46 %，说明运用回归方程的预报准确率有提升、稳定性更好。

5 结论

本文通过分析2015—2017年台风影响场区的26 d浅层风实况、24 h预报数据，分析预报偏差与台风强度、台风与场区方位的关系，找出建立回归方程的4个因子（数值预报925 hPa风速、台风强度、台风方位、台风与场区距离），通过因子试验设计，找到显著性和稳定性最高的浅层风预报回归方程，并对最优回归方程进行数据检验，通过研究发现：

1）不同台风的强度、台风的方位对浅层风预报偏差影响不同，这种影响为非线性关系。

2）场区周围4点算数平均的数值预报925 hPa风场数据与实况偏差最小，最适合作为建立回归方程的自变量之一。

3）利用2015—2016年72段数据，通过因子分析试验发现，台风强度、台风方位两个因子在回归方程中显著性不明显，选取显著性、稳定性最高，且标准差最小的试验3方程作为浅层风预报回归方程。

4）利用2017年36段数据对试验3回归方程效果进行检验，发现回归方程能有效减小预报偏差，且减少较大误差出现次数，回归效果较好。

图5 试验3风速的残差四合一图Fig. 5 Four-in-one diagram of wind speed residuals in test 3

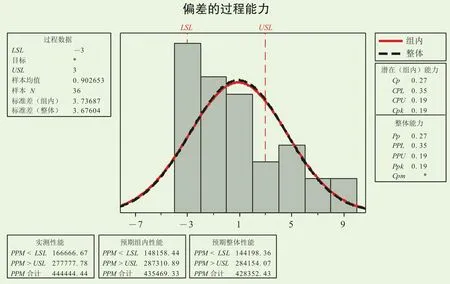
图6 试验3回归方程的效果检验Fig. 6 The verification of regression equation in test 3

表5 试验效果对比Table 5 Comparison of verified results

通过建立风速预报回归方程，可以有效提高24 h预报准确率，但由于场区受台风影响时浅层风数据积累不够多，还需进行资料收集，通过增大样本数据个数改善回归方程。后续研究中还应进行回归方程效果评定，针对台风影响后期风速明显减小时拟合效果不好的情况进行改进提高。