基于量子算法的电热系统双层优化模型*

邓博夫，张铁岩，回 茜，3

(1.沈阳工业大学 电气工程学院，沈阳 110870；2.沈阳理工大学，沈阳 110159；3.国网辽宁省电力有限公司 营销服务中心，沈阳 110006)

可再生能源因其具有清洁、分布广泛等特点受到众多关注，然而新能源发电的波动性和不确定性影响电力系统的稳定运行，导致弃风、弃光现象的存在[1].为了提高能源利用率，多能源系统的整合成为了学术界研究的重点[2-3].其中，电热联合系统由于热电联产机组的技术成熟及热力网络巨大的储能能力已成为目前最为广泛应用的联合系统.然而热电联产机组内在的电热耦合特性制约了电热联合系统的灵活性，以热定电的调度方式导致北方地区冬季供暖时产生大量弃风、弃光情况[4-6].

提高热电联产机组灵活性的常用方法有：电网侧增加电储能、热网侧增加热储能以及应用热泵、电锅炉等能源转换装置[7-9].由于储能元件成本较高，目前无法大规模应用，因此增加电转热装置是当下解耦热电联产机组的最优方式.伴随着分布式发电和能源互联网的快速发展，越来越多的研究集中于去中心化的多能源联合系统[10-11]，同时，系统间的双边和多边交易机制也亟待完善[12].

基于上述分析，本文提出了一种以电力系统为主体，考虑热力系统的能量流动和网络约束的双层优化调度模型.研究了以电价补贴等方式引导热网中的热电联产机组、热泵和电锅炉等电转热机组的决策，从而在新能源发电高峰时段降低热电联产机组的出力，进而减少弃风等现象的发生.提出了一种以实数量子编码优化为基础的求解方式，在利用KKT条件将双层问题转化为单层问题后，用平滑函数将问题线性化，进而求得均衡解.

1 电热联合系统双层优化模型

在电热联合系统的双层优化模型中，电力系统包含燃煤机组、风电机组、电网络和电负荷，热力系统由热电联产机组、热泵、热力管网和热负荷组成.热电联产机组分别向电网和热网出售电能、热能，热泵从电网购买电能的同时向热网出售热能来进行套利.双层优化调度模型结构如图1所示.

图1 双层优化调度模型结构示意图

1.1 上层电力系统调度模型

上层问题优化目标为电网的收益最大化，其主要由三个部分构成：售电收入、购电支出、弃风/切负荷惩罚.目标函数表达式为

CWC+CLC-CLOAD

(1)

上层问题优化的约束为电力系统约束，包含功率平衡约束、电网潮流约束及机组运行约束，表达式分别为

(2)

(3)

(4)

1.2 下层热力系统调度模型

下层问题在电力系统中用以对提供电价修正后的热泵、热电联产机组决策行为进行预测，其优化目标为热电联产机组和热泵总的收益最大化，主要由3部分组成：售电/售热收入、购电支出、二次项成本，其表达式为

(5)

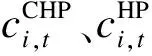
下层问题优化的约束为热电联产机组运行约束、热力系统的能量流动约束及管道约束，热电联产机组的电热出力表达式为

(6)

(7)

热力系统的网络约束包含节点温度约束、热力平衡约束、热力延迟约束、热力损失及能量流动约束等，本文将这些约束简化到相关矩阵中，并表示为

SH×u=v

(8)

式中：SH为系数矩阵；u为节点流入/流出温度变量矩阵；v为热站热出力、热负荷及其他变量矩阵.

(9)

1.3 双层优化问题削减方法

对于含有不等式约束的平衡约束双层优化问题，可以采用拉格朗日乘子法将下层问题利用KKT条件转为无目标的约束[13]，使其成为一个单层优化问题，下层问题转化后的表达式为

(10)

2 基于实数编码量子的优化算法

2.1 下层约束的平滑函数

以第一个热电联产机组的上限约束为例，该约束可以表达为

(11)

利用平滑函数可以将该约束近似为

(12)

隶属度函数可以保证优化过程中其解落在可行域内并逼近全局最优值，其表达式为

(13)

2.2 实数编码量子优化算法

基于等位基因的实数编码量子进化算法采用等位基因的实数编码方式，继承了传统量子比特编码的优点，使种群具有极强的多样性[14-15].在此基础上，采用一种基于等位基因“相对优良性”的混合进化策略，充分利用已知的信息加快收敛速度，同时采用变尺度的变异来搜索未知的空间，等位基因动态的相互转化增强了算法的局部搜索与全局搜索的平衡性.对于“较优基因”，充分利用现有信息，使其在当前最优解的指导下向着当前最优解逼近，并沿途搜索更优解，其表达式为

(14)

(15)

式中：U(-1，1)为-1～1之间的随机分布；r为当前代数；g为最大迭代代数；Δd为允许变异的范围，如当U(-1，1)为负数时，Δd=xi-ximin.

对于“较差基因”则按式(14)和(15)交替进行，即奇数代变异，偶数代趋向当前最优解进行同化.这样的进化方式使其在进化的前期有更好的全局搜索能力，而在进化的后期又有较强的局部搜索能力，且不至于与当前最优解有较大的偏离.优化方法的步骤如下：

1)首先设置种群数M与最大迭代数E，在边界约束内随机产生初始种群，设置e=1；

2)当给定的ε≥0且固定每个x∈X，求解式(13)；

3)对于每个y∈Y，采用量子优化算法求解式(6)，获得最优解x与最优值F，令x*=x，y*=y，F*=F，e=e+1；

4)当迭代次数达到最大值时算法终止，否则令e=e+1并转向2)，可以得到另外一组最优解(x′i，y′i)与最优值F′(x′i，y′i)，若F′>F*，则x*=x′，y*=y′，F*=F′，e=e+1；

5)达到设定最大迭代数之后，得到近似最优解(x*，y*)与NBLP的近似最优值F(x*，y*).

3 实验结果与分析

本文采用IEEE 6节点电力系统和8节点热力系统进行仿真实验，开发工具包括Matlab和优化软件Gurobi.电力系统由一个上下限为69.4 MW/38 MW的热电联产机组和最大功率为40 MW的热泵与热力系统相连接，燃煤机组的出力上下限为200 MW/115 MW，换热站在配热网络中可看作热负荷，联合系统结构如图2所示.

图2 电热联合系统示意图

图3给出了风电24 h内的预测功率，由图3可见，风电在24 h内的波动性较大，峰值与低谷时段风电预测功率相差约100 MW.图4、5分别给出了热力负荷和电力负荷的预测值，从中可以看出，热力负荷和电力负荷在24 h周期内有相反的趋势，这是因为夜晚是用电低谷阶段，白天是用电高峰，供热情况相反.

图3 风电预测功率

图4 热负荷预测

对于现今以热定电模式下，首先要保证热力供应充足，此时由于热电联产机组的成本较低，会提供更多的热能，同时产生更多的电能，供热高峰时段一般为用电低谷时段，此时会产生大量的弃风，传统以热定电模式下的发电机组出力如图6所示，图7为热电联产机组电出力及热泵功率曲线.

图5 电负荷预测

图6 以热定电情况下各机组出力

图7 热电联产机组电出力及热泵功率

从图6与图3的对比中可看出，风电在前8个时间段，即用电低谷时段被大量削减，总弃风量为432.3 MW/h.此时的热电联产机组运行平稳，保持最大出力.而在后半段风电出力较低时，燃煤机组的出力提高，保持电力系统的平衡，减少切负荷的风险.由图7可更直观地看出，热泵的运行功率和热电联产机组的出力基本维持在一个稳定的状态，并未受到风电波动的影响.

当采用基于量子算法的双层电热联合系统模型时，由于电价信号的引导，独立调度中心能够根据价格信号对热力系统的机组进行调整，在双层优化调度模式下仿真结果如图8所示.根据图8可以看出，与以热定电的发电模式相比，热电联产机组降低了出力.在基于量子算法的双层优化模型中，由于电价的引导，在风电较多的用电低谷时刻，热电联产机组卖电的价格会降低，同时热泵消耗电能的价格也降低.在这种模式下，24 h弃风量为234.1 MW/h，相比于以热定电模式多接纳风电198.2 MW/h.

图8 双层优化模型下热电联产机组电出力及热泵功率

为了验证量子算法相比于普通遗传算法的优越性，本文在单层优化后采用遗传算法进行优化，优化的具体参数如表1所示.

表1 遗传算法和实数编码量子优化参数设置

图9对比了两种算法的迭代过程，设机组买/卖电的价格为浮动值，约为500元/MWh，热能价格约110元/MWh，弃风惩罚约1 000元/MWh.由图9可以看出，实数编码的量子算法在初期比遗传算法的收敛速度快，大约在150代左右，遗传算法和实数编码量子算法达到搜索的最优值，分别为640 370和663 756元/MWh.实数编码量子算法的平衡全局优化和局部优化的能力更强，能够更好地避免落入局部最优值，从而得到最优解.

图9 遗传算法和量子算法优化过程对比

4 结 论

本文提出了基于量子优化算法的电热联合系统双层优化模型.该模型包含了电力系统和热力系统能量流动及相关约束，充分考虑了热力潮流中管网的延时及热力市场不完善等因素.通过双层模型上、下层的博弈来实现综合收益的最大化，提出了实数编码量子优化算法，有效解决局部最优及对于变量众多的大系统无法求得有效解的问题，对电热联合系统的综合市场机制及风电消纳等问题具有重要的理论意义和实践价值.