基于CA模型的危险品运输网络节点失效传递研究

何春燕，张凌煊，李 静，李林卿

基于CA模型的危险品运输网络节点失效传递研究

何春燕1，张凌煊1，李 静1，李林卿2

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 国家铁路局市场监测评价中心，北京 100070）

为科学管理危险品运输，本文基于元胞自动机（CA）理论，结合节点负载重分配策略，研究了城市危险品运输网络节点失效传递的动力学行为。研究表明该模型能反映危险品运输网络节点失效的平均传递趋势及规模，能有效辨识网络中关键节点，具有可行性和准确性；加强对关键节点的保护力度，适当提高节点承载力，增强节点自我恢复能力可降低节点失效对危险品运输网络失效传递规模的影响。

公路运输；节点失效；元胞自动机（CA）；危险品运输网络；传递

0 引 言

危险品运输网络（Hazardous Materials Transportation Network，HMTN）是以上下游企业、储存中心、转运中心和交通运输枢纽等为节点，节点间交通路线为边，主要从事易燃、易爆、有强烈腐蚀性和放射性危险物品运输的复杂网络[1]。网络节点作为危险品运输过程中的重要载体，容量有限，一旦发生交通事故或恐怖袭击等突发状况，会直接造成整个HMTN功能受损甚至崩溃。因此，研究节点失效传递行为，加强关键节点识别，对HMTN正常有序运行具有重要意义。

目前复杂网络节点失效问题的研究成果主要集中于以下2个方面：（1）网络性能分析。种鹏云等[1, 2]根据恐怖袭击条件，定义了正常、失效、暂停3种节点状态，并对HMTN级联失效抗毁性进行了定量研究；步琼阅等[3]分析了不同去点攻击策略下成都市HMTN的毁伤阀值及毁伤特点等网络抗毁性性能；郝羽成等[4]考虑现实网络中节点对负载的冗余能力，对节点过载状态下的复杂网络级联失效模型进行抗毁性仿真；胡鹏等[5]将液体透过缝隙自然渗流和复杂网络渗流理论相结合，开发了一种智能评估HMTN节点失效渗流鲁棒性的方法[6]。（2）关键节点识别。王延庆[7]定义了节点“过载函数”，提出了基于负载接连失效的节点重要性评估方法；吴俊等[8]用节点权值演化代替网络拓扑结构的演化，提出了考虑级联失效的复杂负载网络节点重要度评估方法，以识别网络中潜在的关键节点；周漩等[9]通过定义节点效率和节点重要度评价矩阵，提出了一种利用节点重要度来识别复杂网络关键节点的方法。这些研究大都侧重于抗毁性、鲁棒性等复杂网络整体性能分析以及关键节点的识别，其评价指标往往从结果性角度出发，忽略了节点的自我恢复能力，较少深入分析HMTN节点失效传递的动力学行为。

笔者将综合考虑节点突发失效以及节点负载重分配策略，采用元胞自动机（Cellular Automata，CA）模型定量分析HMTN节点失效传递趋势及规模，辨识网络关键节点，以期为HMTN规划与管理提供理论依据。

1 HMTN节点失效定义及传递过程

1.1 HMTN节点失效定义及传递过程

定义1 节点失效是指一定时间和空间范围内，HMTN节点因恐怖袭击、交通事故等突发状况或交通负载渗流（节点负载超过其节点承载能力）而无法继续完成危险品运输任务时的节点状态。

（1）在一定时间和空间范围内，因恐怖袭击、交通事故等突发状况而失效的节点，不具备自我恢复能力，所有关联于该节点的边同时失效，并对其及相连边做删除处理。

（2）因交通负载渗流而“暂时失效”的节点，在其负载重新分配后，具备一定程度的自我恢复能力，可以以一定概率恢复到正常状态。

（3）本文设定初始失效节点为突发失效。

定义2 节点承载力是指在一定时间和空间范围内，HMTN节点所能支撑危险品运输和交通运行的最大数值。计算公式如下[5]：

定义3 节点失效率是指一定时间和空间范围内，HMTN节点突发失效开始直至网络中失效传递规模不再变化为止，失效节点数与总节点数的比值，用来衡量节点失效的传递规模。计算公式如下：

1.2 HMTN节点失效传递过程概述

根据前面对节点失效的描述，本文将HMTN节点失效传递过程分为三个阶段，如图1所示。

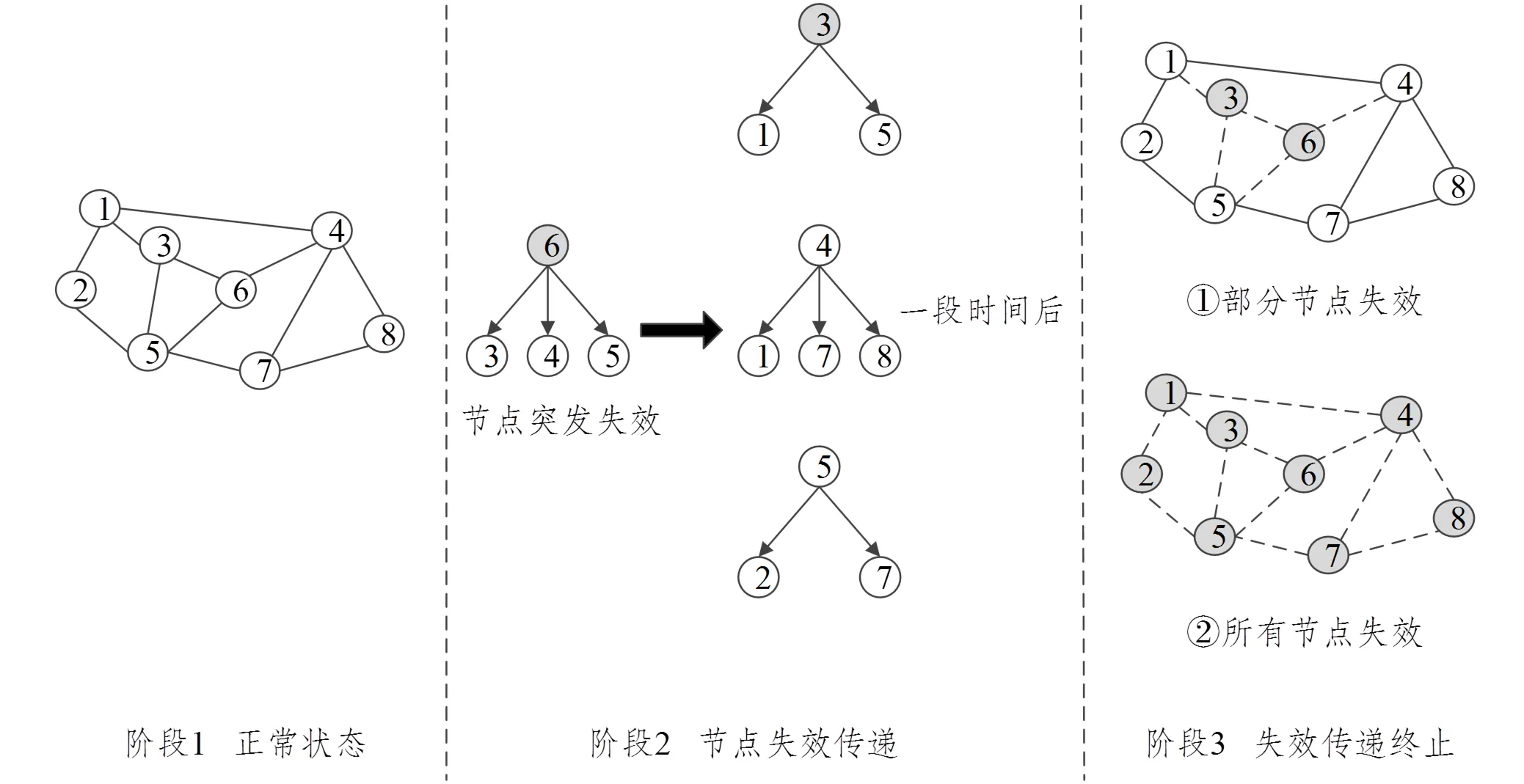
图1 HMTN节点失效传递过程

（1）阶段1，正常状态。网络无任何突发状况，各节点正常运行，无任何不良状态。

（2）阶段2，节点失效传递。节点突发失效，交通负载渗流。例如：节点6突发失效，与之相连节点3、4、5均会受渗流影响而重新配流。

（3）阶段3，失效传递终止。① 部分节点失效：一段时间内，失效节点只有3、6，其余节点仍然正常运行，网络达到一个新平衡状态，即新的阶段1；② 所有节点失效：网络节点接连失效，网络运输功能严重受损，且在一定时段内难以恢复到正常运行状态。

2 基于CA模型的节点失效传递研究

CA模型[10]是一种时间、空间、状态均离散，并按照一定局部规则演化的网格动力学模型，能模拟复杂系统的时空演化过程。该方法已广泛应用于复杂网络，文献[11-16]证实了CA模型在复杂网络性能分析方面的可行性，为本文研究提供了依据。在HMTN中，将网络节点视作元胞，节点间拓扑结构关系用元胞邻接矩阵表示。

2.1 模型假设

根据上述相关定义和节点失效传递过程描述，本文建立基于CA的节点失效传递模型，假设如下：

（1）无向网络。本文关于网络节点失效传递的研究是在复杂网络理论的基础上，为研究方便，假定该HMTN为无向交通网络。

（2）突发状况次数。假设在一定时间内，只发生一次突发状况且使得该节点失效。

（3）交通负载配流策略。按照节点度重分配策略配流，网络节点流量不超过其最大负载限制。

（4）考虑HMTN节点自我恢复性能。因负载渗流而“暂时失效”的节点，在仿真时间内，均能以一定概率恢复到正常状态。

2.2 CA模型

式中：表示元胞空间，即元胞所在空间网点的集合；表示有限状态集，可以根据所研究系统的特点来确定元胞状态；表示元胞邻域，即系统中某个元胞所有邻居节点集合；表示状态转换规则，即元胞状态转换函数。

2.2.1 元胞空间

HMTN元胞空间可以表示为由个元胞构成的一维元胞空间，其中每个元胞表示HMTN的一个节点。

2.2.2 元胞状态

2.2.3 元胞邻域

2.2.4 状态转换规则

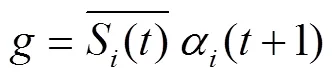
2.3 模型算法

为统计节点失效率，判断节点失效传递趋势及规模，算法过程如下：

step1 初始时刻，随机确定HMTN中任意节点突发失效。

step2 节点突发失效，其邻居节点因节点负载重分配而“暂时失效”。按失效节点邻居节点的节点度比例分配负载，公式为：

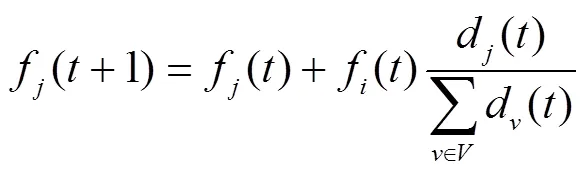
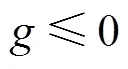
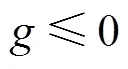
3 案例分析

3.1 原始数据

不同于普通货物的运输网络，危险品运输网络是一种特殊的交通复杂网络，是从道路交通网络中“筛选”出来的，不仅具有危险品运输网络安全风险等属性，还包括道路交通网络的拓扑结构、流量等属性。以一个典型的HMTN（见图2）为实例[5]，相关网络参数值见表1。

图2 某城市HMTN

表1 网络参数值

Tab.1 Network parameter values

3.2 结果分析

根据既有HMTN及其参数，模拟节点突发失效下的传递特性，以识别网络中关键节点，仿真结果如下。

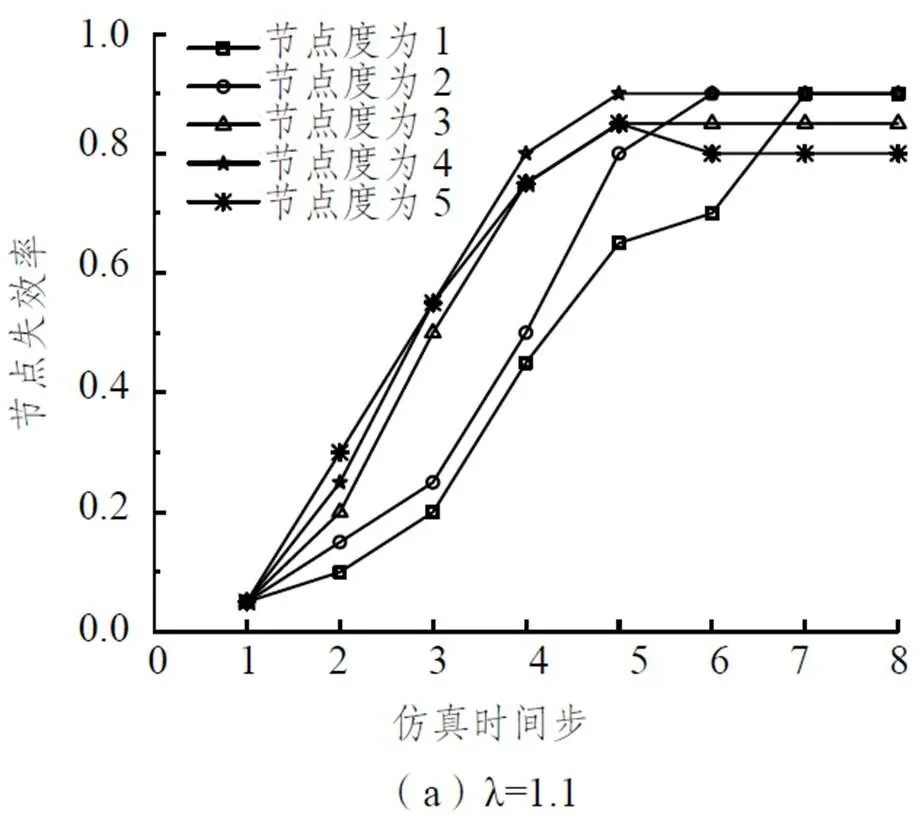
（1）节点失效传递趋势描述

图3 突发状况下节点失效传递图

（2）关键节点辨识

根据节点失效传递速率，可以识别网络中一些潜在的关键节点。如表2所示，对节点重要度进行排序。并非所有高节点度节点比低节点度节点更重要，例如节点18（节点度为2）和节点15（节点度为3）均为低节点度节点，而其重要度排序分别为第4和第5，因此节点重要度排序除了考虑节点度的大小外，还需综合考虑节点在网络中的聚集度、紧密度等。

表2 节点重要度排序

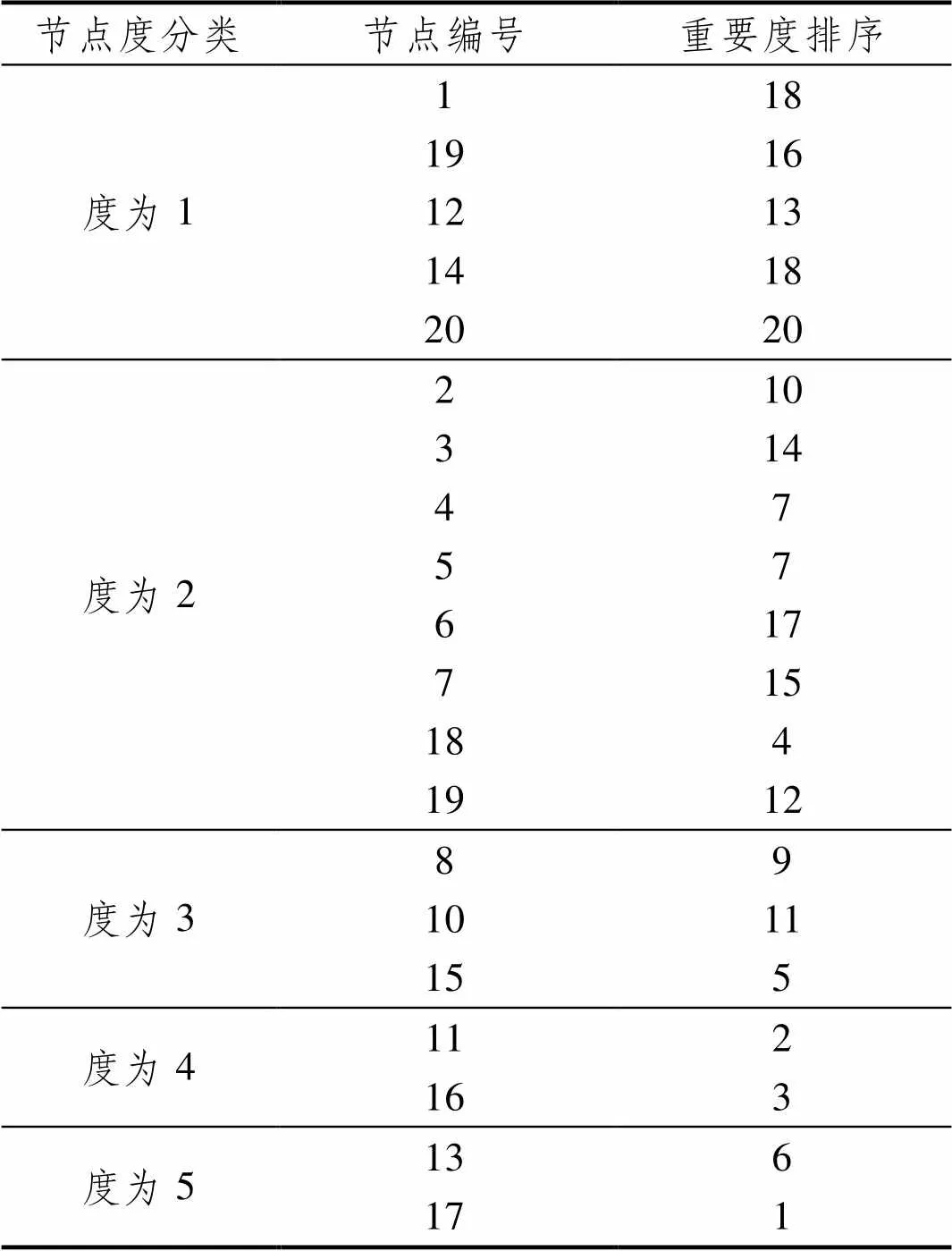
Tab.2 Node importance ranking

（3）不同节点承载系数对HMTN节点失效传递规模的影响

（4）不同节点恢复率对HMTN节点失效传递规模的影响

4 结 论

通过对危险品运输网络节点失效传递过程的建模与仿真，可以得到以下结论：

（1）CA模型可探究突发情况下HMTN节点失效的传递趋势及规模，能有效辨识网络中潜在的关键节点。

（2）高节点承载系数可控制突发状况下节点失效传递规模，因此可适当提高HMTN节点承载系数以降低节点突发失效对网络的损害，这一结论与文献5相同，验证了该模型的合理性与可行性。在相同情况下，节点恢复率越高，越能适应网络拓扑结构和交通行为的变化。

（3）使用CA模型可以定量分析HMTN节点失效传递的动力学行为，但模型中仅将节点状态分为0和1两种状态，未考虑不同失效程度下的节点状态，在未来需要进行深入研究。

[1] 种鹏云, 尹惠. 蓄意攻击策略下危险品运输网络级联失效仿真[J]. 复杂系统与复杂性学科, 2018, 15 (1): 45-74.

[2] 种鹏云, 帅斌. 恐怖袭击下危险品运输网络节点风险评估方法[J]. 中国安全科学学报, 2012, 22 (8): 104-109.

[3] 步琼阅. 基于复杂网络理论的危险品运输网抗毁性分析—— 以成都市为例[D]. 成都: 西南交通大学, 2014.

[4] 郝羽成, 李成兵, 魏磊. 考虑节点过载的复杂网络级联失效模型[J]. 系统工程与电子技术, 2018, 40 (10): 2282-2287.

[5] 胡鹏, 帅斌, 赵佳虹. 危险品运输网络节点失效渗流鲁棒性建模仿真[J]. 交通运输系统工程与信息, 2014, 14 (5): 181-187.

[6] 胡鹏, 帅斌, 吴贞瑶. 危险品运输网络渗流鲁棒性智能评估方法[J]. 中国安全科学学报, 2019, 29 (2): 57-62.

[7] 王延庆. 基于接连失效的复杂网络节点重要性评估[J]. 网络安全技术与应用, 2008 (3): 59-61.

[8] 吴俊, 谭跃进, 邓宏钟, 等. 考虑级联失效的复杂负载网络节点重要度评估[J]. 小型微型计算机系统, 2007, 28 (4): 627-630.

[9] 周漩, 张凤鸣, 李克武, 等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报, 2012, 61 (5): 1-7.

[10] WOLFRAM S. Theory and applications of cellular automata[M]. Advanced: Series on Complex Systems, Singapore: World Scientific Publication, 1986.

[11] 王亚奇, 蒋国平. 基于元胞自动机考虑传播延迟的复杂网络病毒传播研究[J]. 物理学报, 2011, 60 (8): 116-124.

[12] 李辉, 贾晓风, 李利娟, 等. 基于元胞自动机的电网隐性故障传播模型关键线路识别方法[J]. 电力系统保护与控制, 2018, 46 (6): 16-23.

[13] 李钊, 徐国爱, 班晓芳, 等. 基于元胞自动机的复杂信息系统安全风险传播研究[J]. 物理学报, 2013, 62 (20): 1-10.

[14] 叶夏明, 文福拴, 尚金成, 等. 电力系统中信息物理安全风险传播机制[J]. 电网技术, 2015, 39 (11): 3072-3079.

[15] 张柠溪, 祝会兵, 林亨, 等. 考虑动态车间距的一维元胞自动机交通流模型[J]. 物理学报, 2015, 64 (2): 303-309.

[16] 王丹彤, 王芙蓉, 黄凯. 基于元胞自动机的高速铁路列车群追踪运行仿真模型[J]. 铁道标准设计, 2018, 62 (4): 87-91.

Node Failure Transmission of Hazardous Materials Transportation Network Based on CA Model

HE Chun-yan1，ZHANG Ling-xuan1，LI Jing1，LI Lin-qing2

（1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China；2. Market Monitoring and Evaluation Center of National Railway Administration, Beijing 100070, China）

To scientifically manage the transportation of hazardous materials, node load redistribution strategy was combined with the cellular automata (CA) theory to observe the transmission characteristics of urban hazardous materials transportation network (HMTN) nodes. Results show that the CA model can reflect the average transmission trend and scale of the failure of HMTN nodes and effectively identify key nodes in the network; furthermore, it is feasible and accurate. By strengthening the protection of key nodes and improving the bearing capacity and self-recovering ability of the nodes, the impact of failed nodes on the failure transmission scale of the HMTN can be reduced.

highway transportation; node failure; cellular automata (CA); hazardous materials transportation network; transmission

U16

A

10.3969/j.issn.1672-4747.2020.03.016

1672-4747（2020）03-0133-09

2019-08-30

何春燕（1994—），女，湖北荆门人，硕士研究生，研究方向为交通运输规划与管理，E-mail：cyh5161@126.com

何春燕，张凌煊，李静，等. 基于CA模型的危险品运输网络节点失效传递研究[J]. 交通运输工程与信息学报，2020，18（3）：133-141

（责任编辑：李愈）