核心素养为导向的2020年全国Ⅰ卷理科第12题赏析*
林松云
福建省柘荣县第一中学 (355300)
1.试题回放
(2020年全国Ⅰ卷第12题)若2a+log2a=4b+2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 2020年全国Ⅰ卷第12题以指数、对数函数、不等式为载体,体现函数与方程思想,化归与转化思想,突出对逻辑推理、数学运算、数学抽象、直观想象、数据分析等核心素养的考查,注重对思维品质、关键能力的考查,具有很好的选拔功能. 角度一:(特殊值法)逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养,其中包括从特殊到一般的推理.特殊值法就是从已知出发通过一些特例推翻一些错误的结论,从而得出正确的结论.考查逻辑推理、数学运算、数据分析等核心素养. 解:令b=1,则2a+log2a=4,所以1 评析:可以看出此题特殊值法简洁,考生容易想到. 角度二:(数形结合法考虑)数学学科核心素养的直观想象中提出“利用图形,建立起数与形的联系,利用几何图形描述问题,借助几何直观理解问题”.数缺形时少直观,形少数时难入微.本题是以方程的形式呈现,把方程问题转化为函数的图像问题,从而借助函数图像形象直观的解决问题. 评析:转化为函数图像交点问题.考查直观想象、逻辑推理、数学抽象等核心素养. 角度三:(函数与方程思想考虑)严谨性是数学学科的基本特点,命题、结论的推理论证理由需充分、清楚、严格、周密.逻辑推理素养中提出要培养学生重论据、有条理、合乎逻辑的思维品质和理性精神. 而f(a)-f(b2)=2a+log2a-(2b2+log2b2)=22b+log2b-(2b2+log2b2)=22b-2b2-log2b,当b=1时,f(a)-f(b2)=2>0,此时f(a)>f(b2),有a>b2,当b=2时,f(a)-f(b2)=-1<0,此时f(a) 评析:通过已知条件中给的方程转化为比较函数值的大小问题.解法三考查了逻辑推理、数学运算、数学抽象等核心素养. 数学学科六大核心素养内核是数学思维品质、创新意识.在解题教学中,核心价值在于培养学生的思维品质.上述不同的方法体现了不同的核心素养要求.解法一主要是考查逻辑推理素养,解法二主要考查直观想象、数学抽象素养,解法三主要考查了逻辑推理、数学运算素养. 普通高中数学课程标准(2017年)在“实施建议”中提出“树立以发展数学学科核心素养为导向的教学意识,将数学学科核心素养的培养贯穿于教学活动的全过程”,那么解题教学中该如何落实数学学科核心素养? 核心素养指向下该如何设计教案,教案中教学目标要如何体现.学科素养的培养不是一蹴而就,而是日积月累的一个阶段性过程,在教学设计中要思考核心素养的孕育点、生长点,思考每节内容与学科核心素养的有何关联.数学基础知识、基本技能、基本思想、基本活动经验是培养核心素养的“土壤”,教学设计中应该思考让学生理解这“四基”,促进核心素养的提高. 解题教学中,数学问题如何选择,哪些问题才更能落实核心素养的培养.首先问题要有开放性,让学生有思考的空间;要有层次性,调动不同学水平学生有兴趣参与教学活动,让不同水平的学生得到不同的发展;要有针对性,直击核心素养的培养.因此教师在平时应该多研究、探索、实践,理解数学,理解学生,理解教学,提升自己数学素养,才能积累、创新好问题,好试题.2.解法探究

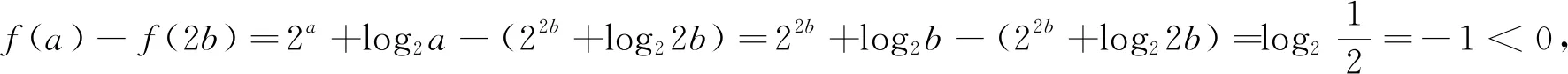
3.解题教学中如何培养数学核心素养
3.1教案设计中要体现数学学科核心素养
3.2解题教学中数学问题设计要体现学科核心素养

