基于动态分析的软件不变量综合技术*

王 博 , 卢思睿 , 姜佳君 , 熊英飞

1(北京大学 信息科学技术学院 计算机科学技术系 软件研究所,北京 100871)2(高可信软件技术教育部重点实验室(北京大学),北京 100871)

软件不变量(software invariant,以下简称为不变量)是软件运行时在程序某位置必须保持的属性(property).不变量可以有多种表现形式,例如前条件(pre-condition)与后条件(post-condition)、循环不变量(loop invariant)、断言(assertion)、在面向对象语言中描述对象属性的类不变量(class invariant)以及描述对象之间关系的结构不变量(structural invariant)等等.

不变量被广泛应用在程序验证、程序理解、程序优化、程序维护、程序缺陷定位以及程序缺陷修复等领域.一般而言,不变量可以被编码为逻辑表达式,从而使用数理逻辑手段进行演算.例如在程序验证中,不变量可以视为规约(specification),通过把程序的语义转化为逻辑表达式,可以使用霍尔逻辑进行演算来验证程序是否满足规约.由于不变量是软件属性的高度抽象,人工构造不变量非常繁琐复杂,因此开发人员一般采用软件分析(program analysis)的方法从软件中自动地综合(synthesize)不变量.

软件分析技术主要包括静态分析(static analysis)和动态分析(dynamic analysis).静态分析不需要运行程序,仅根据程序自身的源码、文档或者可执行文件等等进行分析.为了分析得到不变量,静态分析在程序所有可能执行的路径(path)和状态(state)上进行推理,可以得到可靠的(sound)分析结果.然而,由于静态分析过于复杂,在实际中只能应用在小规模软件上,而且一般只能得到形式较为简单的不变量.动态分析则根据程序的执行踪迹(trace)来分析得到不变量.给定一组输入(例如软件的单元测试)运行程序,动态分析根据程序某位置运行时状态归纳分析结果.由于动态方法只执行全部可能的输入的一部分,并且只覆盖了一部分路径,因此动态分析的结果不保证可靠性与完备性,例如可能遗漏了某些不变量或者生成了错误的不变量.相比于静态分析,动态分析一般效率(efficiency)较高,有更好的可延展性(scalability),而且可以生成形式更复杂的不变量.

早在20 世纪70 年代,软件验证领域就开始了对不变量的研究.早期不变量相关研究主要是基于静态分析方法,例如使用抽象解释[1,2]分析不变量.2000 年左右,研究者们才开始研究基于动态技术来分析不变量.其中,里程碑式的研究工作是Ernst 等人在1999 年提出的Daikon[3].之后,研究人员逐渐开展基于动态分析的不变量综合研究,并且取得了一系列成果.本文的目标是分析、梳理这20 余年内基于动态分析的不变量分析的相关研究工作,以供研究人员快速了解该领域.有关基于纯静态分析的不变量分析方法不在本文讨论范围之内.

为了对该研究问题的进展进行系统地分析和比较,我们首先按以下步骤收集并筛选1999 年以来的相关研究文献.

(1) 使用谷歌学术搜索引擎以及ACM,IEEE,Springer,Elsevier 和CNKI 等论文数据库;

(2) 检索关键字包括在英文引擎中的“program invariant”和“software invariant”以及在中文引擎中的“不变量”和“不变式”等;

(3) 检索时间为1999 年至今的全部文献;

(4) 基于前述步骤检索到的论文,通过人工筛选移除无关论文.之后,浏览文献并移除与动态分析技术无关论文.在此文献列表上,总结出该领域的活跃研究者,进一步在研究者的论文列表中检查是否有遗漏的工作.在选取过程中,主要倾向选取软件形式化、软件工程、系统软件以及程序设计语言等相关领域的会议和期刊.

我们最终选取了90 篇论文,其中绝大多数是所涉及领域的高质量会议和期刊,例如POPL 会议(2 篇)、PLDI会议(10 篇)、OOPSLA 会议(1 篇)、SOSP 会议(1 篇)、CAV 会议(2 篇)、ICSE 会议(14 篇)、ESEC/FSE 会议(5篇)、ASE 会议(8 篇)、ISSTA 会议(7 篇)、ESOP 会议(1 篇)、TACAS 会议(1 篇)、SAS 会议(2 篇)、FM 会议(1篇)、ISSRE 会议(1 篇)、TSE 期刊(6 篇)、TOSEM 期刊(2 篇)、软件学报(2 篇).

图1 统计了2001 年～2019 年的与动态不变量分析技术的发表文章数,从中可以看到该领域的研究趋势.自从1999 年以来,每年都有高质量文章发表,说明相关研究依然十分活跃.该领域的研究获得了一些重要奖项,包括ICSE 会议2009 年[4]和2012 年[5]的SIGSOFT 杰出论文奖,PLDI 会议2018 年[6]和2019 年[7]的杰出论文奖.

国外已有一些与不变量分析技术相关的英文综述论文,与已有的综述[8-10]相比,我们的工作有以下不同.

· 首先,我们总结出基于动态分析的不变量综合技术的研究框架.现有的综述主要以软件验证领域的视角来梳理文献.我们希望在建立统一的研究框架之后,可以打破软件形式化、系统软件、软件工程、程序设计语言等不同领域之间的壁垒,更系统地分析和比较研究成果;

· 其次,本文重点对动态分析相关的不变量综合技术进行综述,对于不变量的种类并不限制.相比Furia 等人的综述[8],我们不仅分析了循环不变量的相关工作,还总结了结构不变量等其他种类的不变量;

· 再次,我们在文献选取与分类上使用了新的视角.我们按照生成不变量的方法将所综述的文献划分为基于模板穷举的方法、基于数值计算的方法、基于统计学习的方法和基于符号执行的方法这4 个类别.在此基础上,我们尝试总结出动态不变量综合技术发展的不同阶段,以方便研究人员掌握该领域的发展脉络并预测发展趋势.另外,我们分析并总结了不变量在软件维护、软件测试和软件调试等相关领域的广泛应用;

· 最后,在上述综述之后,该领域又出现一些新的进展.研究者们不但提出一些新的不变量动态综合方法,还把该技术应用在新问题和新场景上,例如最近两年不变量被应用在信息物理系统错误检测[11,12]和神经网络模型验证[7,13]等领域.我们补充了相关的最新研究成果.

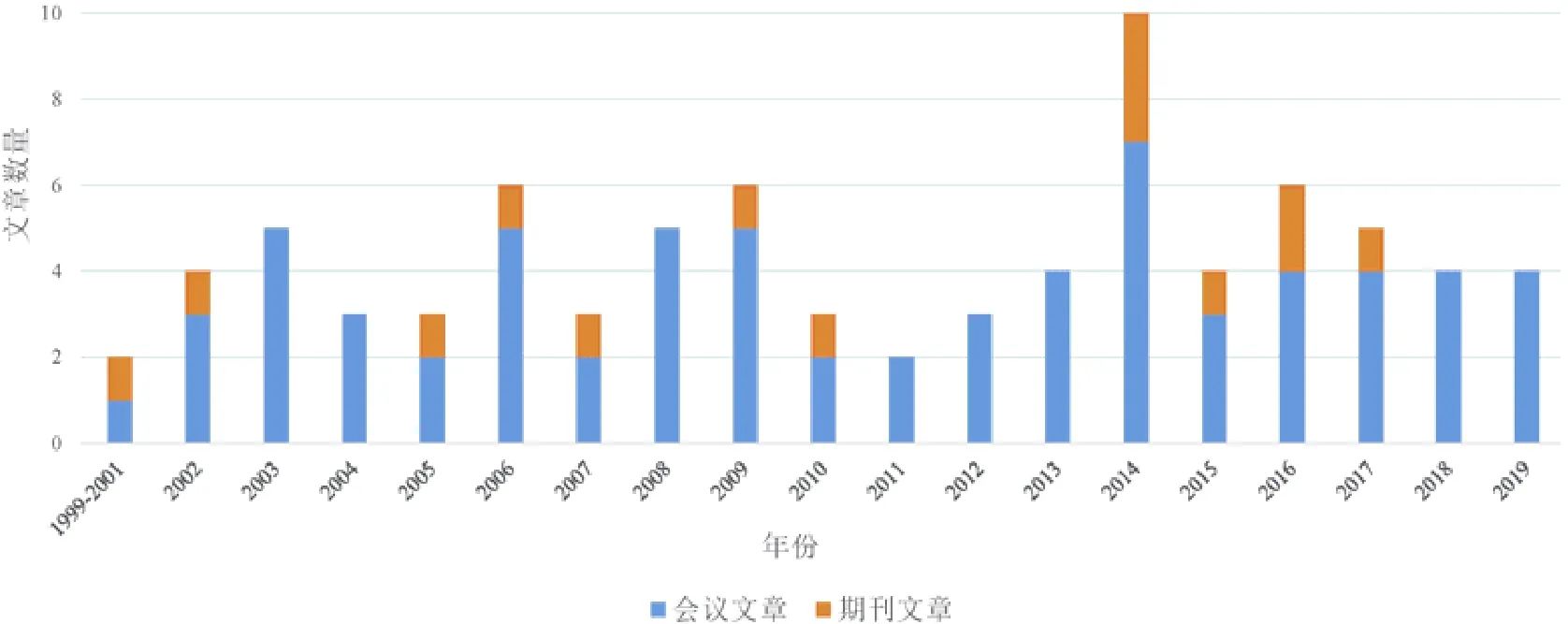
Fig.1 Publication numbers in different years图1 在不同年份发表的文章数

本文贡献可以总结如下.

(1) 系统地分析了基于动态分析的不变量综合技术.通过梳理与该领域相关的90 篇国内外高水平论文,提出了“学习者-预言模型”研究框架概括基于动态分析的不变量综合技术;

(2) 在该研究框架下,我们对于收集到的方法根据其技术特点进行分类,并分析得到该领域的演进趋势;

(3) 系统地总结了基于动态分析的不变量综合技术的相关应用;

(4) 总结了该领域的经常使用的数据集和开源工具.

本文第1 节介绍本领域的基础,包括不变量的概念与形式,提出了“学习者-预言”研究框架.第2 节对已有的基于动态分析的不变量综合方法进行梳理分析,并分析技术演进趋势.第3 节总结动态分析综合不变量的相关应用.第4 节总结常用的测试程序以及重要的开源工具.最后,第5 节总结全文并展望未来研究方向.

1 基于动态分析综合不变量基础

1.1 不变量的概念与形式

不变量的字面是表达“不会改变的量”或“常量”的含义.在计算机程序中,不变量是指在程序某个片段在所有执行过程中需要保持为真的逻辑断言.根据程序的位置不同,不变量约定的名称也会随之改变.例如:在循环初始位置和结束位置都被保持的属性,一般被成为循环不变量;在面向对象语言中,描述对象方法(method)或者域(field)的属性的,一般被称为类不变量.另外,当不变量所描述的对象为数据结构实例(instance)之间的关系时,被称为结构不变量(例如二叉树中一组左、右孩子节点的双亲节点必须相同).

以下给出不变量的形式化定义.

定义1(不变量).在命令语言中,对于任意的可终止程序P,c是P中的命令集合.在关于P的任意输入上,执行到c中命令之前时,程序的状态始终满足的逻辑表达式I,则称I是该位置上的不变量.

根据定义1,我们可以描述不同类型的不变量.例如:当c仅包含一条命令,在其执行之前必须满足的逻辑表达式I为c的断言(assert);若c仅包含循环的第1 条命令以及循环之后的第1 条命令,在这两个命令执行前必须满足的逻辑表达式I成为循环不变量.

在逻辑上,不变量必须保证是正确的,这就要求生成不变量的算法必须是可靠的.然而在程序分析中,尤其是动态分析中,可靠性难以保证.因此,该领域的研究者提出各种方法来生成最可能正确的不变量.

1.2 基于动态分析的不变量综合技术研究框架

本文重点综述基于动态分析的不变量综合技术,其目标是在动态分析的基础上归纳得到不变量.图2 总结了典型的基于动态分析的不变量综合技术的研究框架.

Fig.2 Overview of general dynamic invariant synthesis framework图2 基于动态分析的不变量综合方法研究框架概览

受到预言指导下的归纳综合(oracle guided inductive synthesis)技术[14]的启发,我们提出基于动态分析的不变量综合方法的研究框架,如图2 上半部所示.该框架可以大体分为两个模块,即基于归纳的学习者(inductive learner,后文简称为学习者)模块以及预言(oracle)模块.预言模块也可以被称为教师(teacher).其中,学习者的任务是综合生成不变量,而预言的任务是判断学习者产生的不变量是否正确以及为学习者提供不变量综合用的辅助信息.学习者和预言之间存在交互,交互方式是学习者向预言提出请求(request),请求的内容可以是验证其生成不变量的正确性、程序符号执行的结果、正例、反例等.预言负责回应(response)相应的结果.一般而言,学习者不掌握程序内部细节,视其为黑盒.学习者主要通过预言返回的数据样例等信息归纳产生不变量.预言掌握丰富的程序内部信息,以便能够回应学习者的请求.二者经过有限次的交互后,得到最终的不变量集合.基于此,我们将该研究框架称为“学习者-预言”模型.

预言模块把程序视为白盒,除了掌握程序代码、程序规约(specification)、程序属性(property)等信息之外,还能产生正例(example)和反例(counter-example).值得注意的是:程序规约既可以是程序的完全规约,也可以是测试等形式的不完全规约.为了响应学习者的请求,预言可以执行多种操作.例如:学习者请求验证猜想的不变量是否正确时,预言可以使用测试执行程序验证或者通过静态分析验证;学习者请求提供程序的符号执行结果时,预言可以进行动态或静态符号执行,返回程序中变量的符号表示以及路径约束;学习者请求反例时,预言通过静态分析和约束求解器得到反例并返回.

学习者是不变量综合技术的核心,也是该领域一直以来的研究重点.我们根据所依赖预言提供数据的种类以及学习者所采用的归纳方法,大致将其分为4 类,即基于模板穷举的方法、基于数值计算的方法、基于统计学习的方法以及基于符号执行的方法.

本文提出相关方法的一种划分,可以看出,这几种分类有着明显的递进关系.大致的趋势是生成不变量形式越来越复杂,方法的步骤从单次到循环迭代,依赖预言提供的信息越来越多.值得注意的是:如果某几种方法之间有交叉重叠之处,我们将依据一个方法的主要创新之处来将其归类.

通过上述不变量的综合过程,我们总结对于生成不变量的质量的影响因素以及对不变量综合技术的评价指标,如图2 下半部所示.

影响生成的不变量质量的因素主要包括学习者的归纳能力、时间/内存等约束以及预言提供的信息等.学习者的归纳能力越强,得到的不变量形式越复杂、越精确.由于“学习者-预言”模型可能需要多次迭代,时间/内存等约束会影响最终的生成结果,例如在达到最优解之前因为超时停止,会导致产生次优解.另外,一般而言,预言提供的信息越多,对学习者的帮助就越大,最终得到的不变量集合质量越高.

对于不变量综合方法,我们可以从效率(effciency)、表现力(expressiveness)、精确度(precision)和效用性(utility)这4 个方面对其进行评价.

· 效率是单位时间内某方法生成的不变量数目.对于动态分析而言,效率越高的方法可延展性越好.一些不变量综合方法依赖于插装、动态符号执行等代价较高的动态技术,其运行代价限制了它们在大规模程序上的应用.因此,高效率的方法具有更高的实用价值;

· 表现力是某方法能够生成不变量的种类.一般形式越复杂的不变量越难生成,例如二元不变量难于一元不变量,高阶多项式形式的不变量难于线性形式的不变量.复杂不变量在现实世界中大量存在,生成方法更有表现力意味着其能生成更复杂的不变量,从而更好地刻画软件属性.值得注意的是:表现力虽然从某种程度上可以反映召回率(recall),即发现的不变量占理论上所有存在的不变量的比例,但是二者并不相同.在现有相关论文中,评价方法的表现力往往依赖于不变量的复杂程度,即通过能够生成其他方法理论上无法生成的形式的不变量证明其优势,而不是简单比较挖掘到的不变量的数目;

· 精确度是指所生成的不变量中正确的不变量的比例.动态分析方法一般不保证结果的正确性,对于产生的假阳性(false positive)不变量,需要较高的代价去过滤.因此,高精确度的方法更容易部署为全自动方法,具有更好的实用性;

· 效用性是指所生成的不变量是否满足应用需求的比例.虽然方法的精确度十分重要,但是如果不满足应用的需求,生成大量正确而无用的不变量,也会影响任务的完成.例如在软件验证任务中,不变量过多会导致程序的验证耗时过长,甚至因超时导致任务失败.因此在实际应用中,我们需要精简而正确的不变量集合.效用性与应用类型高度相关.例如,动态监测非法内存访问时,与内存边界有关的不变量有更高的效用性.

2 基于动态分析的不变量综合技术

本节主要在第1 节中提到的“学习者-预言”框架下讨论基于动态分析的不变量综合技术.首先,从学习者的视角来看,根据学习者的归纳得到不变量的方法,我们将当前的基于动态分析的不变量综合技术大致分为4 类:基于模板穷举的方法(例如Daikon[3,15,16]和DIDUCE[17])、基于数值计算的方法(例如DIG[5,18],NumInv[19]和SLING[20])、基于机器学习的方法(例如ICE[21],PIE[22]和DORDER[23])以及基于符号执行的方法(例如DySy[24]和KRYSTAL[25]).本节依次介绍4 个分类.针对每个分类,我们主要介绍该分类整体的技术特点,该分类下已有的重要方法,并简要概括该类方法的优缺点及其适用场景;其次,对预言来说,验证学习者提出的不变量正确性是其核心任务,因此,我们以预言验证不变量的方式将已有方法进行简要归类分析;最后,我们做出小结,分析本领域研究的现状与发展趋势.

2.1 基于模板穷举的不变量综合技术

在基于模板穷举的方法中,学习者在程序上选择需要生成不变量的位置,根据预先设计的谓词模板,与当前位置的变量尝试所有可能的组合之后得到猜想不变量集合,根据预言提供该位置程序正确执行的状态集过滤掉被违反的不变量.预言一般需要执行测试集来收集正确的程序状态返回给学习者,并根据测试等部分规约对猜想不变量进行验证.学习者与预言之间存在一次或者多次交互,最终将不变量集合返回.

最早在1998 年,Vaziri 等人检测动态运行中两个变量是否保持=,＜,＞,≤或≥等比较关系.该工作可视为基于模板的动态不变量分析的早期探索[26].

1999 年,Ernst 等人提出并实现了Daikon[3],并在2001 年将其扩展为期刊论文[15].Daikon 是本领域的里程碑,同时也是应用最广泛的不变量分析工具.Daikon 的学习者是基于模板穷举来生成不变量.具体来说,在程序员指定的程序位置和变量上,学习者根据模板穷举填入变量,得到猜想的不变量集合.之后,学习者将变量提交给预言验证,预言通过运行测试,过滤测试中被违反的不变量,返回最终的不变量集合.例如,有变量a,b和不变量模板x=0,穷举后得到不变量是a=0 和b=0 提交给预言.预言运行所有测试后,发现该位置存在a≠0 的情况,则a=0 被删除,最终输出不变量b=0.学习者的模板可以大致分为一元操作、二元操作、标量的三元操作以及列表变量相关的模板.表1 列出了Daikon 的所有模板.相比之前的早期探索,Daikon 大幅扩充了模板的数量和表现力,增加了多元表达式以及自动添加了求和等重要的临时变量,可用于挖掘更多的列表元素的不变量.Daikon 支持二元比较关系、三元以内的线性关系等等,同时允许用户添加自定义模板.

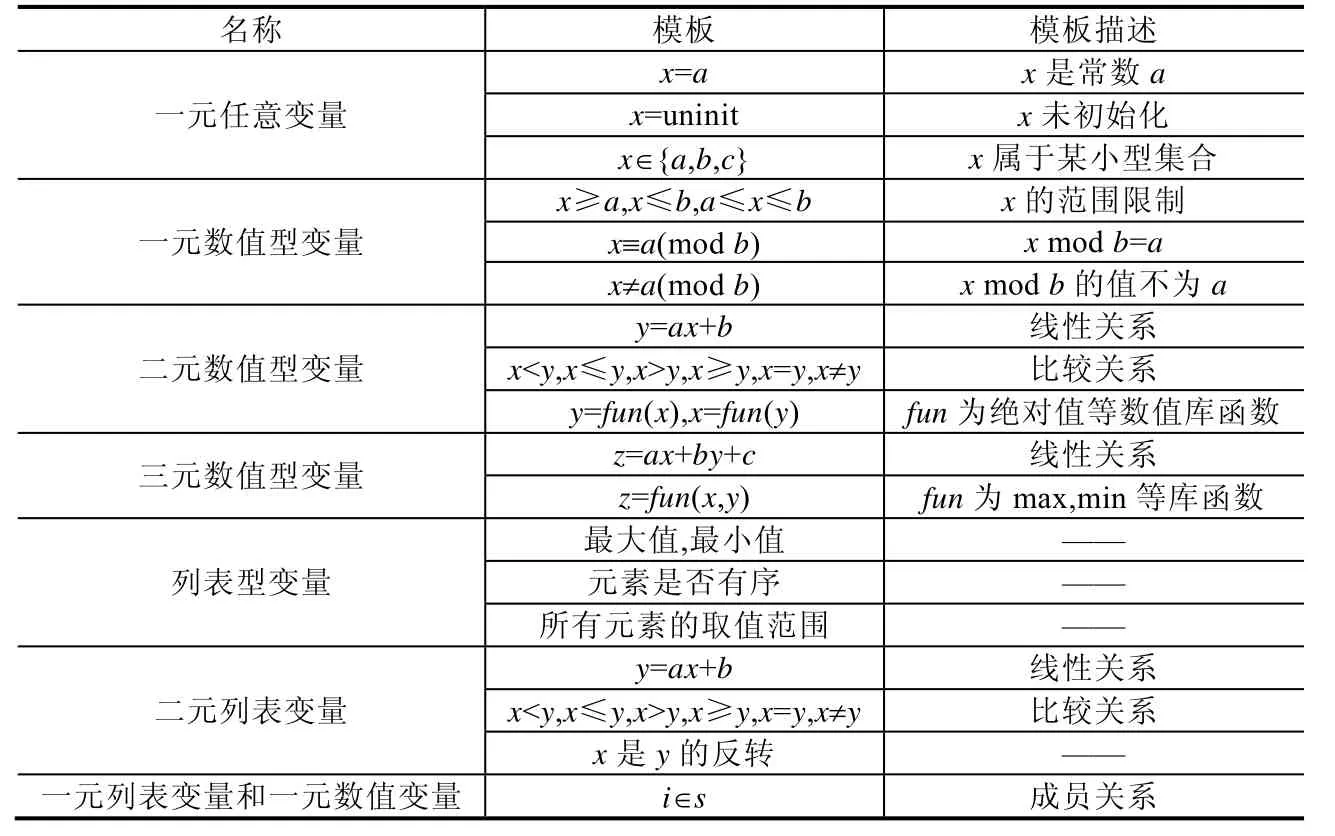
Table 1 Templates of Daikon表1 Daikon 的模板

Daikon 可以在程序的任意位置收集不变量,在收集位置上被观测的变量在执行时的值的集合称为一个样本(sample).若设被分析程序中需要收集的位置数为P,对于某个收集不变量的位置,其所有可能的不变量数为I,在该位置上报告的不变量数为RI,且样本数为L,则Daikon 的空间复杂度为

时间复杂度在最差情况下为

由于实际执行中大多数情况下候选不变量的值是False,会很快被过滤,因此一般情况下的时间复杂度是

由上述3 个公式可知:Daikon 分析的代价很高,特别是I是关于变量个数的高阶多项式.例如:若在当前位置有3 个变量,仅仅模板ax+by+cz=d就会产生152 个可能的不变量[27].Daikon 的空间复杂度和时间复杂度随着程序规模的增大呈指数级增长,导致将其很难扩展在较大规模的程序上.

在Daikon 类似的方法中,学习者算法的复杂度导致其在复杂模板上代价很高,而主要依赖于简单的模板又导致其表现力不足.另外,Daikon 的预言采用单元测试验证不变量的正确性,预言的验证能力十分依赖于测试集的质量[16].为了克服这些缺点,随后,研究人员从学习者和预言两方面对Daikon 的生成方法进行优化.

为了提升Daikon 的学习者效率,Perkins 和Ernst 等人分析了Daikon 算法,发现其简单增量算法中存在多处冗余[27]:首先,当变量x和变量y满足不变量x=y时,对于其他任意的Daikon 模板f,都满足f(x)=f(y);其次,若某变量x满足恒等于常数a,即有不变量x=a,则会产生很多冗余不变量,例如,x=0 必然可得x≥0;再次,面向对象语言中的变量存在层次,生成的不变量可以同时影响多个位置,例如,面向对象中某个公共方法返回处的不变量既是该方法的后条件,又是对象不变量;最后,不变量之间存在蕴含关系,例如x＞y蕴含x≥y.针对这4 个方面的冗余,作者们提出使用增量算法进行削减.另外,为了尽快过滤错误的不变量,他们引入了5 轮次(pass)分析,即:在早期的轮次中分析简单的不变量,后面的轮次中分析复杂的不变量.通过上述加速方法,大幅提升了Daikon 的效率.

在Daikon 等方法中,预言的验证能力高度依赖于测试集的质量,初始测试集的大小和覆盖率等指标直接影响方法的精确度.为了缓解这一问题,张令明等人提出了基于反馈的动态不变量生成方法iDiscovery[28],在预言中引入测试自动生成方法:首先,使用Daikon 生成不变量;然后,将不变量作为断言插装回原程序;随后,使用符号执行在插装后的程序上生成测试,将新测试加入原测试集中;最后,使用加强后的测试运行Daikon.迭代上述过程,直至达到不动点.实验证明了在Daikon 生成的不变量中,该方法可以过滤很多其中的错误不变量,并且能发现新的不变量.值得注意的是,该方法是基于模板穷举的方法和基于符号执行的方法的结合,详见第2.4 节.

Daikon 对结构不变量的支持非常有限,仅能分析简单的数据结构.因此,Malik 等人提出针对复杂数据结构的动态不变量提取算法Deryaft[29].通过将程序的堆(heap)建模为图,其中,图的节点代表内存对象,图的边标记为域,之后在图上分析其性质.Deryaft 把性质设计为模板,然后在图上迭代验证性质是否成立.其所设计的模板主要有可达性(如无环性)、数据结构中描述大小的属性是否与遍历所得的节点数相等、树中不同节点到根节点的距离等等.实验表明:对于结构不变量,Deryaft 的表现力和效用性优于Daikon.

另外,与Daikon 在同一时期,由Hangal 等人在2002 年提出的DIDUCE 也是影响力较大的工作[17].与Daikon相比,DIDUCE 的优势在于:(1) 它是一种全自动的方法,不必像Daikon 一样需要人工指定分析的位置和变量;(2) DIDUCE 通过削减分析的状态,可以延展到较大规模程序上;(3) 对程序输入要求不高,甚至可以使用无测试预言(test orcale)的随机生成的测试.DIDUCE 只分析全局变量上的不变量,缩小了分析的范围.DIDUCE 通过将状态映射为整数上的位(bit),从而将每个插装位置的不变法分析运算约减为几个逻辑位运算,在运行中未改动过的位即是不变量.DIDUCE 拥有动态检查错误的能力,在实验中,它可以发现长时间运行后进入的非法状态.在预言中,与Daikon 使用测试作为规约不同,DIDUCE 使用程序一部分正常运行作为验证手段.

之后,Fei 等人提出了针对动态监控的加速技术Artemis[30],并应用在C 语言版本的DIDUCE 的方法上,提升了该方法的效率.

Hangal 等人将Daikon 的方法移植在硬件验证上,针对硬件设计了新的模板并实现了工具IODINE[31].基于动态分析的不变量一定程度上可以代替人工提取的规范,从而减轻硬件工程师的负担.

在Daikon 的启发下,Boshernitsan 等人提出了方法Agitator,并将其实现为商业工具[32].Agitator 采用的模板包括等式(如x=y),区间(如a≤x≤b),非空(x≠null)以及从源代码中收集的属性,并将动态挖掘出的不变量报告给开发者,辅助他们提升软件的测试集质量.

上述方法的不变量模板主要是基于命题逻辑的形式,即一阶逻辑(first-order logic).后来,研究者也尝试探索使用更复杂的逻辑的模板,例如二阶逻辑(second-order logic)和时序逻辑(temporal logic).

Li 等人使用二阶约束加强Daikon 的一阶命题逻辑不变量,提出方法Meta-Inv[33].二阶不变量又称元不变量(meta invariant),是命题逻辑不变量之间蕴含的不变关系.二阶不变量甚至可以在一阶不变量未知的情况下推导.作者提出了若干二阶不变量模板.例如在数据结构栈中,top 方法入口处的不变量集是pop 方法入口处的不变量集的子集,即可得二阶不变量:“top 方法的前条件蕴含pop 方法的前条件”.作者设计了5 个二阶不变量的模板,用于描述对于不同方法的入口和出口处的不变量集合之间的关系.在Daikon 的基础上,该方法预言也使用测试验证不变量.二阶不变量可以加强一阶不变量的推理,另外还可以扩展到大规模软件上并且有较高的精确度.

Beschastnikh 等人提出Synoptic 方法,根据系统的运行日志自动建模,构造出系统的有限状态自动机[34,35].Synoptic 在日志中挖掘事件的时间序列关系,在时间不变量(temporal invariant)模板的约束下探测模型空间.Synoptic 使用了3 种时间不变量来描述事件发生的顺序关系,包括事件B永远发生在事件A之后、事件B永远不发生在事件A之后、事件A永远在事件B之前.

随后,Beschastnikh 等人提出InvariMint 方法改进Synoptic 方法[36].InvariMint 明确地指定了最终的模型中属性的类型,并且将属性挖掘和属性规约两个机制独立出来,降低耦合.

Beschastnikh 等人提出Perfume 方法[37,38],在Synoptic 方法提出的模型迭代使用基于反例的抽象精化算法不断改进模型,直至模型满足所有的属性.

Beschastnikh 等人提出CSight 方法[39].CSight 为并行程序进行日志分析,挖掘日志中的时间不变量,推理出系统的有限状态自动机.开发者可以使用得到的简洁精确的自动机理解系统的行为或发现缺陷.

Lemieux 等人提出了线性时间规约挖掘方法Texada[40],该方法允许用户自定义任意的线性时间规约模板,同时挖掘用户支持的且在置信区间内的规约.

基于模板穷举的方法简单直观,不依赖于符号执行、约束求解和统计学习等其他复杂技术,而且有Daikon等成熟的工具体系支持.正如第3 节介绍的相关应用中,该类技术的应用范围最广,部分成果也被应用于工业界.该类方法的缺点是其效果高度依赖于模板.模板形式的单调会限制不变量的表现力,但是丰富而语义多有重叠的模板又会降低效用性.因此,该类方法需要用户根据应用特点选择合适的模板.另外,该类方法对测试集的质量需求较高,不但需要测试有较高的代码覆盖率,也需要测试输入有足够的多样性.

2.2 基于数值计算的不变量综合技术

根据第2.1 节中对Daikon[3,15,16]复杂度的分析,随着模板所需变量数以及合法变量数的增多,候选不变量的数量呈指数级增长.受限于模板与变量结合生成的巨大空间,基于模板穷举的技术只适合探索较为简单的线性关系,对不变量表现力有较大限制.例如,Daikon 无法生成三元不等关系的不变量、非线性多项式的不变量、四元或四元以上的相等关系以及嵌套数组关系.为了探索更复杂的不变量,研究者结合数值计算方法生成不变量.在该类方法中,学习者将模板参数化,使用方程组求解方法和多面体近似方法计算不变量,并满足覆盖预言提供的状态集合.在该类方法中,预言通过程序的正确运行的状态集验证学习者猜想的不变量.此外,在部分方法中,预言还可以根据学习者猜想得到的错误不变量使用SMT 求解得到反例反馈给学习者,帮助其在下一轮迭代中产生更好的不变量.

在2012 年,Nguyen 等人首次将数值计算方法应用在动态不变量生成方法上[5].受到静态分析方法中抽象解释等方法的启发,他们使用的数值计算方法主要包括方程组求解和多面体(polyhedra)技术,分别用于处理多元相等关系、多元不等关系.最后,使用SMT 求解技术删除冗余的不变量.具体来说,对于多元相等关系,学习者根据当前变量生成多元多次的等式模板.学习者向预言请求一组正例,将正例中变量的值带入等式,即得到关于系数的一次方程组.根据线性代数方法求解该方程,就得到了等式不变量中的系数.例如,当前位置存在变量a和b,并且需要得到最高项为二次的等式关系,学习者会产生等式方程:

然后,学习者向预言请求多组正确运行中(a,b)的具体值带入上述等式,就可得到关于等式不变量系数c1～c6的一个方程组.若该方程组存在唯一解,使用线性代数方法求解该方程组后就可得到不变量的系数.用类似的方法,将不等关系转化为给定一组点,求一个可以覆盖它们的凸多面体问题.最后,由于不变量之间可能存在蕴含关系,通过SMT 求解器判断不变量之间是否满足蕴含关系,从而过滤冗余的不变量.对于数组不变量,通过将未知数用数组的元素和索引表示,可以将上述计算方法用于数组上不变量的生成.虽然该方法的精确度和效用性不高,但是相比基于模板穷举的方法,其表现力大幅增强.

之后,Nguyen 等人继续将上面的方法进一步扩展为DIG 方法[18]:首先,对于不等关系,DIG 添加了使用几何推理的方法,用下八面体等形状代替多面体,用于得到下近似的结果;其次,将八面体不等式用于数组边界元素上;最后,作者理论分析了所涉及算法的复杂度.

之前相关工作中的不变量都是命题的合取形式,Nguyen 等人首次提出生成析取(disjunctive)不变量的动态分析方法,提升了方法的表现力[41].析取不变量可以用于表现程序分支,是一种十分重要的不变量.例如在程序if(p)a=1; elsea=2;中,析取不变量(p∧a=1)∨(¬p∧a=2)可以表现分支的性质.然而,传统的动态不变量综合方法主要针对合取(conjunctive)、多项式以及凸多面体的不变量,并不适合生成析取不变量.生成析取不变量需要借助非凸多面体,而DIG 等方法使用的加法和乘法仅能描述凸多面体.因此,作者使用了最大加(max-plus)关系代替加法和乘法来描述非凸多面体.同时,针对当且仅当(if-and-only-if)结构,作者使用双最小加(dual min-plus)约束来描述.为了加速计算,作者提出了上述两个算法的弱化版本,使其复杂度降至多项式时间.最后,作者引入静态分析过滤不变量,使用迭代并行的k推导算法.

研究者注意到:在不变量的过滤阶段,SMT 求解技术可以提升过滤非法不变量并产生反例.于是,研究者引入了“猜想-检测”技术,将生成和验证两个步骤统一了起来.

2013 年,Sharma1 等人提出了基于“猜想-检测”的循环不变量生成技术[42].学习者负责“猜想”,使用类似DIG的算法动态推导等式不变量,提交给预言.预言负责“检测”,使用SMT 过滤不满足的不变量,并生成反例返回给“猜想”部分,辅助其生成不变量.“猜想-检测”可视为是一种基于反例引导的方法.算法重复这两个步骤,直至发现满意的循环不变量.

Nguyen 等人提出了在符号执行基础上的基于反例引导的不变量生成技术NumInv(又称DIG2)[19].首先,NumInv 使用DIG[18]得到一组不变量.对于程序位置L上的不变量p,将原程序转换为if (¬p)L.在转换后的程序上运行符号执行.如果符号执行中,L是可达的位置,则p必定不是不变量.对符号执行的环境求解后可得反例,用于指导DIG 的不变量生成.若符号执行中L不可达,则认为p是正确的不变量.在预言的验证部分中,NumInv 使用的符号执行引擎是KLEE,依赖于SMT 求解器.相比于“猜想-检测”[42]方法,NumInv 可以处理不等关系的不变量,表现力得到增强.该方法在基于数值计算的方法基础上结合了符号执行技术.

Nguyen 等人继续改进NumInv[19]的方法,提出了方法SymInfer(又称DIG3)[43].首先,在学习者中设定初始的符号执行最大分支数,在被测程序上运行符号执行,收集各个路径的抽象的符号状态.然后,SymInfer 将抽象状态实例化得到具体状态,进入推理阶段运行DIG 得到候选不变量集合.最后,学习者把不变量提交给预言,预言使用SAT 求解器判断所有符号状态是否能推导出某个不变量,如果推导可满足,就认为是合法的不变量;否则,就求解生成反例,用于返回给学习者,用于下一轮推导过程中指导DIG.学习者和预言之间不断交互,直到得到了稳定的结果后终止.与NumInv 相比,SymInfer 不是将符号执行当做黑盒使用,而是深入符号执行引擎内部,使用实际的符号状态.在验证中,SymInfer 得到的不变量精确度更高,证明该方法的有效性.值得注意的是:NumInv/DIG2 和SymInfer/DIG3 也可视为是基于符号执行的方法.二者都建立在DIG 的基础上,并且DIG,DIG2 和DIG3是同一个团队的连贯研究.为不破坏其完整性,本文将上述三者放在本类别下介绍.

Le 等人提出了SLING,用于在动态分析的基础上提取复杂数据结构中的结构不变量[20].SLING 使用分离逻辑(separation logic)[44]对堆内存建模推理,最终输出的不变量也是用分离逻辑的公式描述的.对于某个数据结构,如列表或树等,SLING 需要设计基于分离逻辑的谓词.然后记录程序在某位置踪迹,得到程序某位置上的堆和栈内存对象变量.根据变量和谓词生成候选不变量集合.最后,使用SMT 模型检查过滤不可满足的不变量.

基于数值计算的不变量综合技术是目前表现力最强的一类方法,可以生成多种复杂的不变量,例如多元多次等式不变量和析取不变量.通过把固定的模板参数化,极大地扩展了可探索的不变量空间,同时也导致不变量空间爆炸式增长.由于面临更巨大的搜索空间,该类方法的精确度和效用性低于其他方法.该类方法对测试集的质量需求非常高,例如DIG 方法使用方程组求解等式不变量时,如果不提供使之恰好有唯一解的数据,就无法解出相应不变量.

2.3 基于统计学习的不变量综合技术

之前所述的方法不论是使用模板穷举还是使用数值计算方法,核心都是使用确定、可解释的算法.近年来,随着统计机器学习技术受到了广泛关注,研究者尝试将统计学习技术应用在基于动态分析的不变量综合技术中.该类别方法一般称预言模块为教师.预言可以通过静态分析的手段验证学习者提出的不变量假设,同时给学习者提供正例和反例.学习者使用统计学习方法,例如决策树(decision tree)和支持向量机(support vector machine)等算法提出不变量假设给预言.当得到最终的不变量集合或达到时间/内存约束后,返回结果.

Sankaranarayanan 等人使用决策树来生成保证程序正确运行的前条件[45].该方法根据程序的输入变量用启发式规则产生一组命题.根据这组命题构造出一个SAT 满足的命题公式,该公式的真值用于表示是否满足某性质(例如是否触发缓冲区溢出).同时,根据各个命题的赋值,可以生成具体的测试输入.运行具体输入可得到该公式的真值(例如该输入触发了缓冲区溢出).之后,以命题赋值及公式的真值为训练集,使用决策树算法从中学习出命题组成的前条件.

Garg 等人提出了基于学习的数值不变量生成技术ICE[21].ICE 分为学习者和教师两个模块.学习者不掌握程序及其规约的任何信息,通过运行踪迹中的具体值来综合出不变量假设.作者将这样的不变量生成器称为黑盒(block-box)方法.教师掌握程序信息和规约,可以为学习者提供训练数据,也可以对学习者返回的不变量假设进行验证,当教师拒绝不变量假设时,会报告提供新的反例.教师和学习者仅通过具体的数据沟通,这样切分的好处是可以让学习者应用机器学习技术.作者发现:仅使用正例和反例用于训练产生的不变量归纳性(inductive)不强,如果把数据之间的推导关系作为训练数据的一部分,则可以减轻过拟合现象.ICE 会根据预定义的数值关系原子命题模板(仅包括x+y＜a或x≠y等简单形式)综合出复杂的不变量.

随后,Garg 为ICE 的学习者设计更复杂的学习算法[46].作者提出了针对逻辑蕴含的决策树算法.同时,理论证明该算法的收敛性,以及如果存在不变量,则该学习算法必然能在有限次迭代中发现.

Padhi 等人发现:ICE 等方法所用的原子命题需要事先用给定的模板定义,限制了不变量的搜索空间.当这些方法生成的命题无法区分正确输入和错误输入时,就不能产生正确的不变量.他们提出PIE 方法,不再需要提供命题模板,而是用基于搜索的程序综合来生成[22].

Ezudheen 等人发现,ICE 生成的不变量并不适合用于程序验证,因为程序验证需要霍尔子句(Horn clause)进行程序推理.作者提出了HORN-ICE 方法,将ICE 的思想应用于生成霍尔子句形式的不变量上[47].霍尔约束是非线性的不变量,为了解决这一挑战,作者提出了基于决策树的学习算法来从样本中学习.作者从理论上证明了:如果存在不变量,该算法可以在多项式时间内找到.随后,Neider 等人在HORN-ICE 的基础上提出了SORCAR方法[48].SORCAR 的学习者在每次交互中,尽量挑选与所验证属性最相关的谓词来生成不变量.

Gehr 等人提出了新的基于机器学习的黑盒方法提取交换性规范(commutativity specification)[49].交换性规范是指两个操作可以交换顺序,在多线程程序验证中十分重要.作者收集数据时采用类型感知采样技术,得到足够多样性而且冗余少的数据集.该高质量数据集可用于过滤冗余的谓词.最后使用谓词生成公式覆盖当前的样例集合,以得到最终的不变量.

Zhu 等人提出了自动生成形状规约的方法DORDER[23].给定一个数据结构的定义和执行踪迹,DORDER 可以在自动生成描述形状和顺序的谓词.首先,DORDER 对数据结构使用随机测试技术产生一组”输入-输出对”(input-output pair);然后,DORDER 自动地分析数据结构,得到一组原子命题;最后,使用机器学习算法根据踪迹学习原子命题.

Zhu 等人提出了数据驱动的受约束的霍尔子句(constrained Horn clause)求解方法LinearArbitrary[6],该方法能使用任意的原子谓词来任意地组合成受约束的霍尔子句.该方法由反例制导的抽象精化验证(counterexample guided abstraction refinement)部分来采样有代表性的正例和反例,并提供给机器学习工具链.机器学习工具链由两层模型组成,用于归纳得到不变量.该方法的验证模块也使用到了基于数值计算方法的多面体求解方法.

Brockschmidt 等人认为,动态分析下生成不变量是搜索出程序已经运行的状态的上近似(over approximate)公式,从某种角度就是统计学习问题.他们提出了技术Locust 用于学习结构不变量[50],用于描述堆对象的形状(shape).Locust 定义了一套分离逻辑公式的文法来描述不变量空间.给定一个初始文法节点,Locust 根据当前状态在机器学习模型的指导下展开非终结节点,直至生成一个合法的公式.

近年来,不变量也与新场景和新问题结合起来.信息物理系统是软件与传感器等硬件结合的系统,在与现实世界的交互过程中需要构建复杂的模型,因此往往难以靠人力进行精确地分析和验证.信息物理系统在使用中会产生大量数据,Chen 等人利用机器学习方法学习其中的不变量[11,12].作者使用了监督模型,即收集正常运行以及非法运行状态下的数据,使用支持向量机算法训练出分类器,用于描述系统变量之间的不变关系.作者使用了变异测试来产生非法运行的数据.

基于统计学习的方法一般采用形式较为简单的不变量模板,表现力受到限制.有的综合方法依赖于较为复杂的学习算法,结果会有不确定性,也影响了综合方法的精确度和效用性.同时,类似神经网络等模型可解释性较低,难以对生成的不变量给出形式化证明.理论上,该类方法可以实现跨项目的不变量预测,但是可迁移性仍需实验验证.该类方法效率较高,适用于需要快速产生不变量的场景.

2.4 基于符号执行的不变量综合技术

上述的3 类方法的学习者主要依靠程序执行踪迹和反例分析得到不变量,而忽视了许多代码文本自身的信息.在此类方法中,学习者除了请求具体执行的数据,也会请求程序符号执行(symbolic execution)的结果,即变量的符号表示和路径约束.除了能得到程序的语义信息,也可以根据需要将符号执行的约束进行求解,预言既可以根据约束的可满足性来验证不变量,也可以产生具体测试输入来增强已有测试.

在2008 年,Csallner 等人最早将符号执行应用在动态不变量生成技术上,提出了方法DySy[24].学习者向预言请求软件的运行状态时,除了在测试上运行的具体执行的状态,也会请求符号执行的状态.预言部分在使用测试进行具体执行的同时进行符号执行.当遇到分支时,符号执行使用具体程序的执行流而非像传统符号执行探索其他路径.当具体执行结束时,符号执行中保存的就是该具体执行的路径条件和变量的符号表示,即获得了本次执行的前条件/后条件,由预言将其返回给学习者.学习者将所有测试的前条件/后条件合并后,即可得该程序的不变量.与Daikon 相比,Dysy 生成的无关不变量更少,提升了方法的精确度和效用性.

同一时期,Kannan 等人提出KRYSTAL 技术,基于符号执行提取结构不变量[25].KRYSTAL 技术提出了一种新的符号执行的变体:普遍符号执行.该变体不会映射赋值运算中的左值,例如程序x=1;y=x+1;中左值y的符号表示是x+1 而非传统符号执行中的2.KRYSTAL 首先通过普遍符号执行收集程序的路径条件和变量的符号表示,使用二者生成局部谓词.由局部谓词生成局部不变量的模板.在这一组模板上执行传统的动态不变量分析.在实验中,KRYSTAL 生成了很多之前方法无法生成的高质量的结构不变量,提升了方法的表现力和效用性.

符号执行的核心思想是将程序中的具体值抽象为符号值,并在符号值上运行程序.符号执行可以探索程序中的路径,并且可以产生覆盖某条已探索路径的具体输入.符号状态可以通过约束求解技术得到具体状态,如前文所述NumInv/DIG2[19]和SymInfer/DIG3[43]就在基于数值计算的方法基础上辅助符号执行技术.另外,符号执行的一个典型应用是自动生成测试.如前文所述,iDiscovery[28]使用符号执行生成高覆盖率的测试提供给Daikon,以生成质量更高的不变量集合.

基于符号执行的不变量综合技术的使用前提是目标程序必须支持符号执行,该类别方法的优势和劣势都可以追溯至符号执行技术自身的优缺点.符号执行的优势是能够获得程序的语义信息,使得学习者能在掌握代码信息的情况下归纳综合不变量.同时,这类方法对原始测试的质量需求也不高,因为可以根据符号执行求解出高覆盖率的具体测试输入来补全当前测试.相对而言,该类方法生成的不变量精确度较高.然而,符号执行也面临许多挑战,例如路径爆炸、内存建模、约束求解以及对浮点数和并发等功能支持不足等.这就需要目标程序满足一系列要求,例如程序所需的第三方库都已被建模以支持符号执行;程序仅有串行执行模式;程序没有浮点计算,没有过于复杂的内存对象和复杂的循环结构等.该类方法适用于规模较小、结构简单或者测试不充足的程序,适合对不变量的精确度要求较高的场景.

2.5 预言的验证方法

在前4 节中,我们主要介绍学习者综合不变量的过程中采用的不同归纳方法.在“学习者-预言”的研究框架内,预言主要承担不变量正确性验证、提供正例/反例、实施符号执行和实施具体执行等.在预言的多个功能中,验证学习者提出的不变量的正确性是最重要的,因此我们主要介绍预言中不同的验证手段.其他预言相关问题,例如运行程序方式等详见前述方法细节,不在此进行讨论.在本节中,我们主要介绍预言中不同的验证方法,并举例介绍典型技术.预言主要使用的验证手段有测试、程序一段时间内的正常运行、静态分析等.

· 测试是软件的部分规约,软件单元测试的运行状态可以视为正确的状态.因此,预言常用测试来检测学习者提出的不变量猜想.如果不变量违反了测试中出现的状态,预言则拒绝该不变量.使用测试验证不变量正确性的代表的技术有Daikon 及其衍生的相关方法、DIG、DySy、KRYSTAL 等;

· 操作系统和网络服务器等软件等需要长时间运行,在这些程序中,可以将程序一段时间内的正常运行视为正确的状态.在这些运行上归纳出的不变量,可以用于检测后续运行的状态.代表技术有DIDUCE以及其衍生方法、信息物理系统中异常检测等;

· 在有的方法中,预言掌握程序的完全规约和属性等信息,可以使用静态分析手段验证不变量的正确性.另外,预言还可以通过约束求解给出违反当前规约的反例,反馈给学习者辅助下一轮的不变量生成.使用静态分析的代表方法有ICE 及其衍生方法、DORDER、Locust 等.

2.6 小 结

本节尝试总结该领域大体的研究现状、发展脉络以及领域分布等情况.表2 对主要的研究方法进行总结,包括方法名称、相关论文、发表的会议/期刊名称、发表年份、方法类型以及生成的不变量类型.该表按照方法的年份排序,方便读者发现并分析研究趋势.

从现有方法出现的时间来看,依次出现的是基于模板穷举的方法、基于符号执行的方法、基于统计学习的方法以及基于数值计算的的方法.基于模板穷举的方法最直观简单,因此出现得最早.该类方法的相关研究主要集中出现在2000 年～2010 年之间.Daikon 不但是该类方法的开创者,也是使用动态分析综合不变量的先驱工作.基于符号执行的的方法随后出现,由于符号执行的自身限制,导致该类方法论文数量仅有2 篇.基于统计学习的方法虽然最早出现在2008 年,但是该类方法在2014 年ICE 出现之后才涌现该领域代表性的研究工作,即使用“学习者-教师”模型,为学习者提供反例指导不变量的生成.基于数值计算的方法出现于2012 年,并且近几年依然有该类方法的论文出现.相比于之前的方法,该类方法不再拘泥于固定模板,而开始使用参数化的模板,能够生成的不变量的表现力大幅增强.我们可以分析出:根据出现时间的先后顺序,基于动态分析的不变量综合技术整体上经历了方法从简单到复杂,依赖信息从少到多的演化趋势.

从现有方法生成的不变量类别来看,最多的是多项式不变量,其次是时间不变量和结构不变量,其他形式的不变量只作为个例出现.我们认为,出现该现象主要有3 个原因:(1) 软件验证技术对这3 种类型的不变量需求较多;(2) 这3 种类型的不变量相对其他类型的不变量更容易生成和验证;(3) 整体的研究活跃,相关的实验对象和开源工具较多.

从研究的领域分布来看,当前已有方法主要来自于软件工程、程序设计语言以及验证领域.其中,基于模板穷举、基于数值计算和基于符号执行的方法主要发表在软件工程领域的会议和期刊上,例如ICSE,ASE,TSE 等.基于统计学习的方法则主要发表在程序设计语言和验证领域的会议和期刊上,例如PLDI,OOPSLA,CAV 等.在查阅文献的过程中,我们发现不同领域之间的一些术语也存在差异,例如预言模块在不同领域中称呼不同,在验证领域的文章中多被称为“教师”(teacher),而在软件工程领域的文章中没有统一的称呼,多用诸如“测试预言”或”规约”等具体描述.而且文章中介绍相关工作的部分也多是介绍自身领域,较少涉及其他领域的相关工作.说明不同领域的研究团队之间的合作与交流需要加强.

Table 2 Summary of dynamic analysis based program invariant synthesis approaches表2 基于动态分析的不变量综合方法总结

3 基于动态分析综合的不变量的相关应用

不变量作为程序规约的一种形式,可以在软件开发的各个阶段发挥出关键作用.不变量在程序的设计、编码、测试、验证、优化和维护中都扮演着关键角色.例如,本领域的先驱Daikon 中提出了一些可能的应用,例如增强文档、辅助调试和缺陷修复、增强测试、辅助静态验证[3,15,16]等等.近年来,随着物理信息系统和深度神经网络等新领域研究的展开,也有研究者使用动态分析产生的不变量在新场景下保证软件的质量.本节介绍基于动态分析提取的不变量的主要相关应用.

3.1 动态错误检测

基于动态分析综合的不变量需要运行程序获得执行踪迹,这使得该技术能够很好地与其他软件动态分析技术结合起来.一般而言,动态监测错误方法可以分为直接验证模型以及“训练-验证”模型.直接验证模型是指运行时指定不变量模板,可以直接用于验证运行时状态.“训练-验证”模型是指先在一部分运行数据上综合得到不变量(训练阶段),之后用于监测后续的执行(验证阶段).为了提高不变量的质量,训练阶段可以使用单元测试或者有代表性的正常运行数据.

(1) 直接验证模型.

直接验证模型的代表有杀菌剂(sanitizer)技术.最初,杀菌剂技术用于动态监测内存对象的边界溢出(bounds overflow)等错误,目前也支持指针双重释放、浮点数精度不合要求、整数溢出等未定义行为、多线程错误以及类型错误等.以内存对象溢出错误检测为例,其大致思路是使用指针访问内存时,为了保证是合法的访问,指针ptr必须满足不变量(ptr≥base)∧(ptr＜base+size).其中,base是目标内存对象的基址,size是该内存对象分配时的大小.该不变量意味着指针访问必须在内存对象的界内,从而杜绝上溢出(overflow)和下溢出(underflow)漏洞.在程序分配内存时,杀菌剂会给每个内存对象动态记录base和size,即填充模板得到不变量.当触发非法访问时,杀菌剂会抛出警告或直接终止程序.代表性杀菌剂技术有AddressSanitizer[51],LowFat[52,53]和EffectiveSan[54]等.尤其是AddressSanitizer 等杀菌剂被集成在Clang 编辑器中,发现了现有软件中大量的安全漏洞.

(2) “训练-验证”模型.

“训练-验证”模型的代表有Daikon[3,15,16]以及DIDUCE[17].以Daikon 为代表的相关技术使用单元测试训练[24,28,31-33],即在单元测试的运行踪迹上收集不变量.而以DIDUCE 为代表的相关技术会首先运行一段时间程序,在这个过程中收集不变量,并将其用于监视之后的运行状态.二者适用于不同的场景,前者适用于测试比较充分的软件,如库(library)等;后者适用于运行数据量庞大或者需要长时间运行的软件,如信息物理系统.接下来,我们介绍一些代表性应用.

Wang 等人将Daikon 应用在并发程序(concurrent program)上[55].相比于传统的串行程序,并发程序线程之间的交互非常复杂,难以分析.作者将不变量和调用图结合起来,用于监测并发程序中的缺陷.Baliga 等人将Daikon应用在内核“后门”的监测上,提出了方法Gibraltar[56,57].Gibraltar 在训练阶段得到内核数据结构的不变量,其中包括内核中控制和非控制相关数据结构.在之后的运行中,如果不变量被违反,则认为发现了后门.如第2.4 节中所述,Chen 等人利用“训练-验证”模型在物理信息系统上生成不变量,用于监视制水机的工作状态[11,12].马骏驰等人使用基于模板的动态不变量分析技术监测高辐射空间环境下软件系统的软错误[58].Lorenzoli 等人使用不变量监视系统状态,并在执行进入错误状态时尝试修复[59].

3.2 调试和缺陷定位

在调试和缺陷定位中,被违反的不变量可以帮助开发者缩小可疑的代码和输入的查找范围,分析出错原因,从而辅助程序员更好的理解、定位和修复缺陷.早在2002 年,Raz 等人就将Daikon 用于检测输入数据的一致性上[60].随后,不变量分析技术也被用于自动缺陷定位技术上.

在统计调试(statistical debugging)中,通过猜想程序运行时在某处需要满足的不变量,通过统计谓词违反情况来自动定位缺陷[61].该方法与基于频谱的定位技术互补[62].谢涛等人通过比较软件不同版本之间变量值的差异来定位缺陷[63].Liblit 等人利用统计方法判断出导致程序出错的不变量[64].Brun 等人利用机器学习方法挑选出最可能揭示缺陷的不变量[65].Groce 等人使用Daikon 帮助开发者理解多个版本中的同一个缺陷[66].

3.3 程序验证

在软件验证中,需要耗费大量人力为程序添加注解.开发者普遍认为,添加注解的代价大于其收益,因此在开发实践中不愿采用验证技术.基于此,研究者发现,基于动态分析综合的不变量可以辅助开发者实施验证技术.基于动态分析技术综合得到的不变量是根据程序执行的数据样例归纳得到的,在不掌握代码信息的情况下,很难保证分析结果的正确性.但基于动态分析的不变量较为高效、精确并且不需要复杂的人工操作,依然被应用在程序验证上.另外,由于动态分析和静态分析技术的互补性,也有研究者将二者结合起来克服各自的缺点.

Nimmer 等人探索了将动态分析和静态分析结合起来解决生成程序形式化规约的问题[67].通过Daikon 生成不保证正确性的不变量,然后使用静态分析进行验证.静态分析可以保证结果正确.作者发现:即便在小测试集上,动态分析得到的不变量的质量也足够静态分析使用.同时,作者也证实了Daikon 方法的有效性,相比静态分析,Daikon 生成的不变量的准确度和召回率都在90%以上.

动态分析工具和静态分析工具都可以辅助开发者添加注解.Nimmer 进行实证研究对比二者在辅助用户添加注解的作用[68].作者选用的静态分析工具Houdini 和动态分析工具Daikon,使用二者生成程序属性提供给用户.实验证明,二者都起到了积极作用而且效果互补.其中,Daikon 能让用户发现更有表现力的不变量,同时动态不变量的不正确性造成的阻碍很小.新手程序员认为,Daikon 提供的信息更有帮助.

Polikarpova 等人在实证研究中对比了Daikon 动态挖掘出的合约(contract)与人工定义的合约[69],发现基于动态分析生成的不变量可以用于增强人工添加的合约,但是并不能产生全部的人工合约.相比于人工合约,Daikon 生成了大约5 倍数量的合约,但是只覆盖了其中的60%,而且大约1/3 的合约是无关的或者是错误的.作者还发现,代码的一些度量指标与Daikon 生成不变量的质量相关,例如行数和类的继承深度等.

合约规范(contract specification)是软件验证和调试的重要手段.Schiller 等人通过实证研究调查程序员实际开发中合约规范的使用情况和效果[70].作者发现:动态不变量可以使程序员更好的理解程序的合约,并实现了工具Celeriac 用于将动态不变量自动植入合约.

Schiller 等人提出了VeriWeb 方法[71],使用Daikon 降低人工添加规约的代价.在实证研究中,探索时间和资金代价与开发者添加的规约数量的关系,从实际的经济角度来审视软件验证的可行性.

由于神经网络等机器学习模型结构复杂、可解释性较低,难以应用传统方法进行验证.有研究者使用不变量分析技术对其辅助验证.Gopinat 等人使用凸面体不变量自动推理深度神经网络的形式化属性[13].通过神经网络模型的输入和输出建立前条件/后条件推理关系.同时,作者也研究了输入和网络内部层的推理关系.Zhu 等人使用不变量指导程序综合方法生成可验证的程序来辅助强化学习模型的验证[7].

如前文所述,动态分析挖掘的不变量在时序逻辑验证中也有重要应用[36-39,40,72].通过生成系统中的有限状态自动机来判断事件之间存在的时序逻辑,从而验证程序的模型.

3.4 软件测试

软件测试是与动态不变量分析紧密结合的技术,测试可以指导不变量的生成,不变量反过来也可以给测试反馈.研究者将不变量分析技术应用于测试生成、测试选择、变异测试等领域.

测试选择的目的是选取测试集中最有效的子集来运行,从而减小测试代价.传统上,研究者一般使用代码覆盖率度量测试的有效性,即:通过分析代码的文本结构有多少被执行过来判断测试质量,覆盖越高的测试被认为质量越好.Harder 等人提出使用语义覆盖情况来选择[73],即检查一个测试覆盖多少软件不变量.作者通过该语义评价标准选择更有效的测试集.谢涛等人使用该指标选择测试[74].类似地,Pacheco 等人使用不变量过滤无效的测试,并预测测试的结果[75].

软件剖析(profiling)技术有助于帮助开发者指定测试计划.Elbaum 等人对软件剖析策略进行了实证研究[76].作者制定了多个评价指标,包括代码覆盖率、错误检测能力以及Daikon 输出不变量的质量等.

Gupta 等人发现,覆盖率良好的测试不一定在生成不变量上表现良好.因此,他们提出了不变量覆盖标准,并使用该标准指导测试生成,最终证实了可以生成更精确的不变量[77].

根据测试的执行状态归纳得到的不变量可以用于测试生成.Yuan 等人使用Daikon 在初始测试集上得到的不变量用于生成软件的集成测试[78].谢涛等人根据不变量的抽象操作用于指导自动生成单元测试[79].在d’Amorim 等人的单元测试自动生成技术的实证研究中,Daikon 的不变量是生成指导之一[80].Csallner 等人使用Daikon 生成的不变量与静态分析结合用于指导测试生成[81].

变异测试是衡量测试集质量的技术,通过植入大量已知的人造缺陷来判断测试的查错能力.然而,变异是否与原程序语义等价是不可判定问题,需要复杂的人工验证去排除.Schuler 等人认为,违反了程序不变量的变异更容易违反原程序的语义.若此类变异没有被测试检测出来,则更值得人工验证是否是等价变异[82].

AJAX 技术是Web 2.0 技术的重要组成部分,AJAX 通过客户端与服务端的复杂异步交互来支持在客户端动态修改网页的DOM 树.这也使得传统的网络应用测试方法不适用于AJAX.Ali 等人利用动态提取的状态不变量使AJAX 的测试自动化[4].

3.5 软件维护

当软件交付使用后,需要软件维护来修复缺陷和修正需求.不变量作为规约的一种形式,可以在该过程中起到重要作用.在Daikon 的最初论文中,作者就提出不变量可以应用在软件维护中,例如提升文档质量、辅助软件修复等方面[15,16,83].

McCamant 使用不变量分析技术预测组件升级可能引入的缺陷[84].通过Daikon 生成系统旧的组件的操作抽象,将其用于检查更新的组件.

Perkins 等人提出了ClearView 方法,使用不变量指导软件自动修复[85].ClearView 在程序的正确执行中学习得到不变量,当监测到缺陷发生时,查看被违反的不变量.之后,ClearView 生成满足不变量的候选补丁,再观察打补丁之后的程序的后续运行,留下最有可能正确的补丁.

也有研究者使用基于动态分析的不变量用于可靠性计算.Ding 等人使用Daikon 挖掘的不变量计算在线运行软件的可靠性[86].周远等人提出计算可靠性的方法是:在Daikon 提取的不变量中提取出失效数据,再提供给可靠性计算模型Nelson 得到最终结果[87].

Wei 等人使用合约在给定的错误执行上自动修复程序[88,89].作者使用前条件/后条件作为合约,用于发现缺陷并尝试修复.

4 常用实验对象与重要开源工具总结

本节总结第2 节中不变量综合方法常用的基准实验对象(benchmark test subject)以及重要的开源工具,以方便读者检索.

4.1 常用实验对象

为了有效地评估不变量综合方法,需要合适的程序作为实验对象.一般而言,为了增强实验的可信度,实验对象程序一般需要具备以下特征:(1) 程序需要有多样性(不能只考虑某一种类型的程序);(2) 实验程序集需要有一定规模(包括程序总数以及每个程序的规模);(3) 程序需要是实际的算法或项目(而非作者定制的程序);(4) 程序需要提供足够的预言(包括高质量的测试、规约、属性描述等).

本节对第2 节中常用的实验对象进行总结,结果见表3,该表总结了程序集名称、使用的编程语言、首次使用的时间、常见的用于生成的不变量类型以及使用的不变量综合方法的名称.其中,常见不变量类型是指该数据集被用于生成该类别的不变量,数值代表等式以及不等式等不变量类型,结构代表结构不变量,霍尔代表霍尔子句不变量.

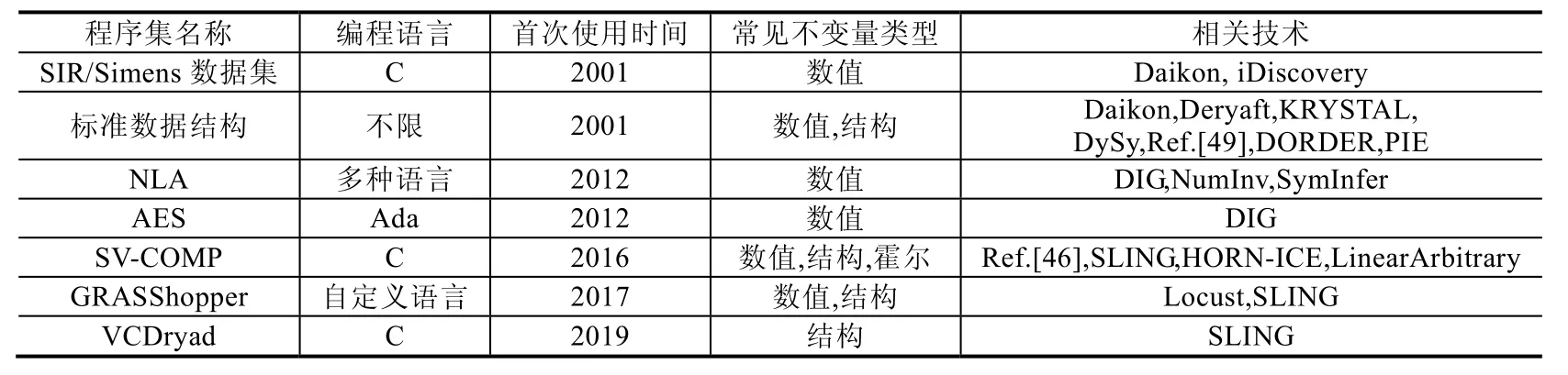
Table 3 Summary of frequently used experiment subject programs表3 常用实验对象总结

SIR/Simens 程序集包含C,Java 等多种编程语言的程序,被广泛应用于软件测试等相关研究中.该程序集的应用类型比较广泛,同时也有较大规模的程序.其中,tcas 是经常被使用的程序.SIR 程序集中每个程序都拥有大量的测试用例和一些植入了缺陷的版本.

标准数据结构包括常用基础数据结构,例如无环列表、有环列表、有序列表、二分查找树、AVL 树、堆、栈等.常见的标准数据结构程序包括C 语言中的glibc 和Java 语言中JDK 对应的包.标准数据结构常用于验证结构不变量的综合技术.

NLA(nonlinear arithmetic)包括27 个C 语言程序.该程序集的程序规模较小,每个程序在20 行左右.该程序集涉及复杂数学运算,包含非线性不变量.

AES(advanced encryption standard)包含27 个Ada 程序.该数据集包含多种不同类型的不变量,总计有868行代码以及25 个函数.

SV-COMP 是依托TACAS 会议举行的软件验证比赛.在2019 年的TACAS 会议上进行了第8 届比赛,并将在2020 年举行第9 届.以2017 年的比赛为例,其中包含超过8 900 个验证任务,每个任务提供了C 语言程序以及相应的规约.任务类型包括溢出、内存安全以及并发安全等问题的验证.

GRASShopper 是一个验证工具,它提供了基准程序集.该数据集是其自定义的编程语言.

VCDryad 是软件验证中常用的基准程序集,其中包含153 个堆内存操作相关的C 语言程序.

从表3 中我们可以发现:针对不同类型的不变量综合方法之间采用的数据集之间存在一些交集,例如标准数据结构被用于生成数值不变量和结构不变量的实验中;而在相同类型的不变量综合方法间,数据集存在很大的多样性,目前还没有一个较为公认的基准程序集.同时,我们可以发现实验对象大多来自库、算法以及数据结构的实现,这从侧面反映了当前方法可延展性普遍较低,应用在大规模软件项目上依然存在困难.

4.2 重要开源工具

不变量综合工具是重要的基础软件框架,支持着验证、测试以及维护等多个研究方向,因此一直以来备受研究者的重视.本节总结前文中出现的重要的开源不变量综合工具,见表4.该表展示了工具的名称、相关文献、论文发表时间、最新版本发布时间、支持的语言和工具的网站.为方便读者查阅,该表按照工具的发表时间排序.其中,参考文献可以检索工作采用的不变量生成算法,发表时间是该工具最早提出的年份,最新版本发布时间可以展示工具的更新和维护情况,同时可供读者根据时间选择对应版本的工具链.支持语言可以方便读者选择合适的工具.表中工具的下载地址收集于2019 年11 月.

Table 4 Summary of tools for dynamic analysis based program invariant synthesis表4 基于动态分析的不变量综合工具总结

5 总结与展望

不变量分析与动态分析是结合了软件验证、系统软件、软件工程和程序设计语言多个学科的重要研究领域,本文讨论二者结合下的基于动态分析的不变量综合方法.自Daikon 以来,该领域得到研究者们的持续关注,新的研究进展不断涌现.学术界的一些研究成果也已经在工业界落地,广泛应用在验证相关的商业工具上,例如IODINE[31]和Agitar[32]等.本文提出该领域的研究框架,即“学习者-预言”模型,并按学习者产生不变量的方式将其分类.正如前文所述,本文根据学习者和预言的交互方式、学习者内部算法以及预言提供信息的不同,不变量综合方法大致可以分为4 类:基于模板穷举的方法、基于数值计算的方法、基于统计学习的方法、基于符号执行的方法等.我们尝试梳理方法之间异同以及该领域整体上的演化进程.之后,本文讨论了动态分析生成的不变量在软件错误检测、软件调试、缺陷定位、软件验证和软件测试等领域上的相关应用.最后,本文总结本领域的重要实验对象程序集以及工具.

经历20 余年的发展,基于动态分析的不变量综合方法已经初步构建出一个研究体系,同时也存在一些有待研究的问题.下面我们讨论该领域还存在如下值得进一步研究的问题.

(1) 结合更多静态分析方法

本文主要讨论动态分析基础上的相关研究.然而,动态分析与静态分析有各自的优势,也有各自的短板,二者的结合可以良好地弥补对方的缺点.另外,不变量分析作为软件静态分析的传统问题之一,存在大量成熟的解决方案,势必存在对动态分析领域有所借鉴的方法.通过第2 节、第3 节可以看出,已有一些相关方法结合了静态分析技术,例如反例指导下的程序综合等.我们可以看到,当前的方法主要是浅层的结合,即仅仅把静态分析技术视为黑盒应用.我们认为还需要分析二者的内部原理,加深二者的结合层次.例如,在分析大规模程序时,如果为预言添加访问上下文的谓词,上下文敏感分析(context sensitive program analysis)就能与基于归纳产生的不变量结合,从而形成新的“上下文”,从而提升相关的程序分析和验证方法的性能.

(2) 提升当前不变量综合方法的性能

正如前文所述,当前基于动态分析的不变量综合技术主要在规模较小、功能特定的程序集上验证,在大型实际项目上部署相关技术依旧面临很大挑战.而且,在工业界应用的方法还是以基于模板穷举的方法为主.这些从侧面说明许多当前已有方法的性能还不足以大规模实用化.通过第2 节我们可以发现:目前已有方法主要集中在提升表现力上,需要研究者更多地提升综合方法的效率、精确度、效用性等其他方面的性能.

(3) 提出更多特定类型不变量的综合方法

根据第2 节不变量综合方法的分析,我们可以看到针对特定类型的不变量综合方法逐渐增多,例如提出时序逻辑、二阶逻辑以及分离逻辑描述的不变量.我们认为:依然存在很多未知类型的不变量还没有被挖掘,有待研究者以新的视角去发现.也可以从应用的角度出发,通过限定应用范围,设计出高精确度且高效用性的不变量综合方法.

(4) 与新的应用场景结合

通过第3 节可以看出,基于动态分析综合的不变量已经成功应用于很多领域,例如软件测试和软件验证等.从历史上看,该领域也一直尝试在与新的应用场景结合,例如早期被应用于多线程程序的验证,以及近年来被应用在信息物理系统错误监测和神经网络模型验证等新领域上.我们还需要积极寻找新的应用场景,例如近年来备受关注的区块链技术和物联网技术.这些领域对软件正确性验证有着很高的需求,与不变量的应用场景十分契合.在已有技术的基础上,我们需要充分分析新的场景的特点,提出针对新问题的解决方案.

(5) 实验对象和工具

通过第4 节,我们可以发现目前该领域的实验对象普遍存在一些问题,例如程序规模不大、程序类型过于单一以及实际工程项目较少等等.我们认为:针对不同的不变量类型,需要统一的高质量实验对象集,从而使新的方法验证更有说服力.另外,Daikon 作为本领域的成熟工具的代表,极大地推进了该领域的发展,在研究中经常被用于基准工具.然而,在Daikon 之后还没有新的不变量综合方法的成熟工具能起到类似的作用.我们认为,结合新的不变量综合方法的成熟工具能在本领域的研究中起到十分重要的作用.