车辆装备维修器材消耗预测方法研究

朱倩倩

摘要：本文运用移动平均数法和贝叶斯方法对车辆装备维修器材消耗规律进行了探索研究，针对不同消耗规律数据进行预测，丰富了车辆装备维修器材消耗预计的思路和方法。下一步可着手开发维修器材数据分析和消耗预测的软件和系统，实现数据的自动化处理，提高预测工作效率。

关键词：移动平均数法;贝叶斯方法;车辆装备;维修器材;消耗

Abstract： In this paper， the consumption law of vehicle maintenance materials was studied by moving average method and Bayesian Method. According to the different consumption law data， the prediction was carried out. It enriches the ideas and methods of vehicle maintenance materials consumption. In the next step， we can start to develop software for data analysis and consumption prediction of maintenance materials， improve the efficiency of forecasting work by automating data processing.

0  引言

车辆装备维修器材消耗规律是维修器材管理工作的核心和基础，维修器材消耗量预测的准确与否直接关系到维修器材筹措、申请和供应等活动的科学性，关系到维修器材保障效益，因此必须对维修器材消耗规律进行探索，对消耗量进行科学预测。针对部队进行维修器材保障工作以历史经验和维修器材相关消耗标准为主要依据造成的维修器材积压与短缺严重、保障效益低等问题，运用装备保障、维修器材管理学、维修工程、统计学等理论，立足于车辆装备维修保障体制，依托可得的消耗数据，对维修器材消耗规律进行深入研究具有重要的意义[1]。

维修器材消耗数据是维修器材消耗规律的外在表现和直接反映，研究维修器材消耗规律可以从维修器材消耗数据入手。但是，维修器材品种众多，消耗影响因素复杂，因此，可得到的用于研究维修器材消耗情况的消耗数据也不尽相同。为此，在广泛调研和收集资料的基础上，总结归纳得出消耗数据类型，并给出了相应的数据分析和处理方法[2]。

不同的方法和模型，有着不同的特点和适用条件。因此，对不同类型的消耗数据，对消耗数据呈现出的不同特点，很难用一个统一的标准和模型来解决所有的维修器材消耗预测问题。为此，运用了多种方法和模型对维修器材消耗预测进行研究，解决了维修器材消耗预测的问题，实现了消耗数据与预测方法的对应。

1  器材消耗模型

1.1 移动平均数法

装备每年在基层单位正常训练过程中，有些单元发生故障后要进行换件修理，这样就产生了检修消耗数据。表1给出了某型车辆历年检修时消耗火花塞的统计数据。

为方便计算，可以将表1中某型车辆历年检修时消耗火花塞的统计数据统一换算成每年20台车辆保障训练、每年保障时间为0.5年时，火花塞检修消耗数据。尝试使用移动平均数法对下一年火花塞检修消耗数量。

移动平均数法中的“平均”是取预测对象的时间序列中最近一组实际值（或历史数据）的算术平均值，其中的“移动”是指参与平均的实际值随预测期的推进而不断更新，可以简单地推导出移动平均数法的计算公式。

移动平均数序列与原时间序列相比，前者比后者平滑，它是滤除了原序列的某些干扰后的结果，因此更能体现出原序列的趋势变化。

按趨势递推原理，以xt作为t+1期检修消耗的预测值，即

移动平均数法对时间序列中数据变化的反映速度及对干扰的修匀能力，取决于N的值。随着N的减小，移动平均数法对时间序列数据变化的反映敏感性增加，但修匀能力下降;而N增大，移动平均数法对时间序列数据变化的反映敏感性减小，但对时间序列的修匀能力却上升。所以移动平均数法的修匀能力与时间序列数据变化的敏感性是矛盾的，两者不可兼得，因此在确定N的时候，一定要根据时间序列的特点来确定[3]。

1.2 贝叶斯方法

车辆装备在等级维修过程中，有些单元要进行换件修理，这样就产生了等级维修消耗数据。

设D=（t1，t2，…，tn）表示车辆维修器材消耗样本数据，π（t）是车辆维修器材消耗的先验分布概率密度函数，π（t|D）表示车辆维修器材消耗的后验分布概率密度函数，f（t）为通过车辆维修器材消耗样本数据D=（t1，t2，…，tn）而获取的车辆维修器材消耗样本分布概率密度函数。

在连续条件下，车辆维修器材消耗的后验分布概率密度函数π（t|D）为[4]

其中，a和b分别为t取值范围的上限值与下限值。

可以看出，器材消耗的后验分布概率密度函数与先验分布概密度函数和样本分布概率密度函数的乘积成正比。

2  示例分析

【例1】以表1中某型车辆历年检修时消耗火花塞的统计数据为例，已知2020年装备实力为26台，训练时间为0.4年。试用移动平均数法预测2020年的火花塞消耗。

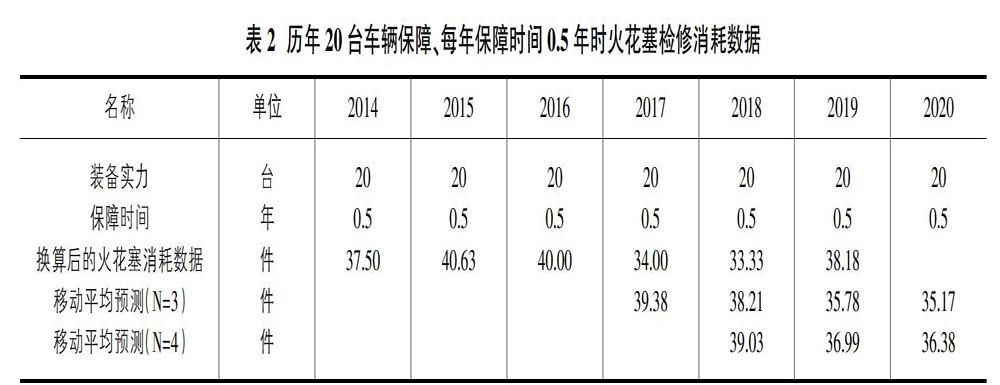
解：为方便计算，首先将表1中某型车辆历年检修时消耗火花塞的统计数据统一换算成每年20台车辆保障、每年保障时间为0.5年时，火花塞检修消耗数据，如表2所示。

通过计算可知，当N=3时，用移动平均数法预计2020年20台车辆保障、每年保障时间0.5年消耗火花塞数量为35.17，当N=4时，用移动平均数法预计2020年20台车辆保障、每年保障时间为0.5年的火花塞消耗数量为36.38。

由于2020年车辆实力为26，保障时间为0.4年，所以，当N=3时，用移动平均数法预计2020年车辆检修时消耗火花塞数量为;当N=4时，用移动平均数法预计2020年车辆检修时消耗火花塞数量为。

由表2中所列的结果看来，由移动平均数法计算后所得到的新数列，其数据起伏波动的范围变小了。移动平均数法有较好的抗干扰能力，可以在一定程度上描述时间序列变化的趋势。移动平均数法，使用起来比较简单，但是由于受加入平均值之中的前面年份火花塞消耗数据的影响，预测结果会出现滞后偏差，如果近期内情况变化发展较快，利用移动平均数法预测就不太适宜。这是由于一次移动平均数法对分段内部的各数据同等对待，而没有强调近期数据对预测值的影响。

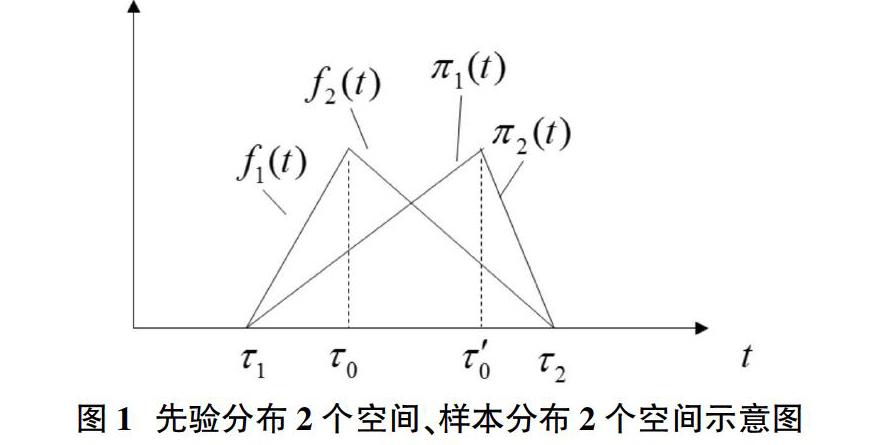
【例2】已知某部队车辆装备在2020年定期维修时发动机空气过滤器的消耗情况。通过判断，该部队消耗发动机空气过滤器的样本分布函数类型为三角形分布，参数为τ1=6，τ2=12，τ0=8。同时，对其它单位消耗发动机空气过滤器的数据进行组合，得到该部队消耗发动机空气过滤器的先验分布函数类型仍为三角形分布，参数为τ1=6，τ2=12，τ0'=8。当先验分布、样本分布均由2个空间构成时，其示意图如图1所示。试运用贝叶斯理论，判断该部队2020年消耗发动机空气过滤器的后验分布，并对2020年车辆装备定期维修时发动机空气过滤器消耗进行预计。

可以看出，2020年6月～8月发动机空气过滤器的消耗单调递增，变化速率较快;8月～9月发动机空气过滤器的消耗仍为单调递增，但变化速率逐渐趋于平缓;9月～12月发动机空气过滤器的消耗单调递减，一开始下降速率较快，到后期趋于平缓。依据2020年发动机空气过滤器消耗后验分布，还可以确定任意时间段发动机空气过滤器消耗的比例，这样可以实现发动机空气过滤器的精确化保障。

3  结束语

本文运用移动平均数法和贝叶斯方法对车辆装备维修器材消耗规律进行了探索研究，针对不同消耗规律模型进行验证，丰富了车辆装备维修器材消耗预计的思路和方法。本文选用的模型复杂程度、预测精度、工作量各不相同，下一步应该对各种消耗预测模型作全面比较，并给出統一的评价标准。消耗数据的处理及有些预测模型的计算工作量较大，下一步应该着手开发维修器材数据分析和消耗预测的软件和系统，实现数据的自动化处理，提高预测工作效率。下一步可以考虑从仿真的角度研究维修器材消耗规律。上述问题有待于后来者进行更进一步的深入探讨。

参考文献：

[1]高崎.军械维修器材管理学[M].北京：国防工业出版社，2012.

[2]Corchado J M， Brian L. A Hybrid Case-Based Model for Forecasting [J]. Applied Artificial Intelligence， 2001， 12（2）：105-127.

[3]潘红宇.时间序列分析[M].北京：对外经济贸易大学出版社，2006.

[4]Clair L.Alston. Case studies in bayesian statistical modelling and Analysis [M]. Queensland University of Technology， 2013.