分形理论在模拟电路故障诊断中的效果分析

盛沛

摘要：提出了一种利用分形理论中的盒维数算法对模拟电路故障进行分类的方法。首先对模拟电路故障状态进行输出信号样本采集，其次对所采信号进行盒维数计算并取得状态区间，最后利用所得状态区间对故障状态进行判别以实现故障状态的区分。仿真结果表明，该方法能够有效对模拟电路的故障进行区分。

关键词：分形;盒维数;模拟电路

Abstract： A method is introduced to classify analog circuit faults by using the box dimension algorithm in fractal theory. Firstly， the fault state of the analog circuit is sampled， then the box dimension is calculated and the state interval is obtained. Finally， the fault state is distinguished by the obtained state interval. The simulation results show that this method can distinguish the faults of analog circuits effectively.

0  引言

分形理论是用来刻画对象的不规则性和自相似性的有力工具，在处理复杂非线性系统中具有独到之处[1]。合理运用分形理论，提取有用的诊断信息，不仅可以定性，而且可以定量地分析系统的工作状态。如果抛开采样精度及存储深度的限制，模拟电路故障信号特征与分形理论的描述是十分吻合的。

模拟电路的各种故障现象往往与其运行状态存在着对应联系。在一些技术部门中经常会存在这样一种现象：对于一些常见的故障，有经验的业务骨干往往可以通过某个测点电压波形形态的变化，判断出哪个元件出现了怎样的问题。事实上，在各专业都有这种“听音诊脉”的业务骨干存在，他们有的看一眼波形、有的听一下噪声，便可判断出装备处于何种运行状态。从这一现象出发，本文研究了相应的模拟电路中的分形理论。目的在于将该种现象提炼、转化为可供利用的故障特征提取方法。

1  分形维数计算

数学家Mandelbrot于1967年在《Science》上发表的一篇文章中提出一个关于英国海岸线长度的著名问题：每个临海国家都有海岸线，而每一个海岸线都具有一个长度值，可是这个值要如何计算出来却是个问题。通常人们可能会采取折线近似来计算，该方法首先要确定度量单位r，r表示度量海岸线长度的折线段长度，然后再通过长度r计算所需要折线段的数量N（r），由此可以得到海岸线长度L（r）=r·N（r）。但是，海岸线包含了许多海角和海湾，这就对折线段的尺度r的选择产生了限制——选取过大就会忽略海角和海湾等因素。若尺度r变小，那么需要被测量的地方N（r）将随之变大。Mandelbrot通过对折线法的研究，给出了一个规律：rD·N（r）=常数。其中D与r值变化无关，通常是非整数。由此，分形维数早期雏形逐渐形成。

分形是具有以非整数维形式填充空间的形态特征，而分形维数是描述分形最主要的参量，简称分维[2]-[3]。分形包括规则和无规则分形两种。对于规则分形，其自相似性、标度不变性是无限的，即无论在何种尺度上对其观察都具有一样的自相似性质;而无规则分形自相似性是近似的或统计意义上的，可借助规则分形的思想进行求解[4]。与欧氏几何图形维数取整数值不同，分形维数能够取得分数值。Hausdorff于1919年提出分数维数，并建立了维数理论和测度。在此基础上，逐渐发展处诸多分形维数计算方法，如盒子维数、信息维数、网格维数、关联维数等。其中盒子维数与其它维数计算方法相比，在故障诊断时的经验估计和计算复杂度都比较简单，故障诊断速度也比较快，其具体计算方法如下：

若非空集合F，且F？奂Rn。N（F，δ）代表覆盖F所需直径最大为δ集的最少数目，则F的上、下盒子维数为：

根据特征性不同，某些等价形式也会用这一定义。假设N（F，δ）取以下几种情形，那么上述的极限值不变：

①与F相交的δ网格立方体数量;

②直径最大为δ，覆盖F的互不相交小球的最大数量;

③半径为δ，中心在F里的互不相交的小球的最大数量;

④边长为δ，覆盖F的立方体的最小数量;

⑤半径为δ，覆盖F的闭球的最小数量。

对N（F，δ）的取值进行比较就可以获得这些定义形式的等价性。Rn中δ网格立方体可表示为：[m1δ，（m1+1）δ]×…×[mnδ，（mn+1）δ]。很显然的，当n的取值不同時，这一网格立方体有不同的含义，譬如：n取1时，网格立方体为区间;n取2时，网格立方体为正方形;n取3时，网格立方体为立方体……其中n取2时的情况也是本文所要研究的重点。在实际应用中，假设一平面集F，计算盒维数，就需要建立一些盒子，定义其边长为δ，盒维数值就是F与δ相交的数量。该盒维数值可通过函数lnN（F，δ）-lnδ的斜率估计出来。

2  盒维数算法应用建模

对于模拟电路信号特征的提取，分形理论主要针对的就是分形维数值，通过分形维数就可以识别它们的分形特征。假设现有表征同一故障状态的某一被测信号，对其进行采样可得到两组故障数据。可能由于采样起始位置、长度、采样周期的影响，其形态特征会有所不同，但是基于分形特征自相似的理论，在相同测度下其分形维数是比较接近的[5]。这是将分形理论应用于电路故障诊断的理论依据。基于此，可利用分形维数作为故障特征，以期达到区分故障状态的目的，具体步骤如下：

步骤1：选取非线性模拟电路中N种典型的故障状态，包括正常状态在内共计N+1种。

步骤2：在第i种状态下，对测试点输出电压信号进行测量并进行盒维数值的计算，则该盒维数值即为一次实验样本。

步骤3：重复1、2步骤m次，取得m个状态i下的样本，求取平均值及区间范围。

步骤4：重复上述步骤N+1次，取得所有状态i的样本区间及均值。

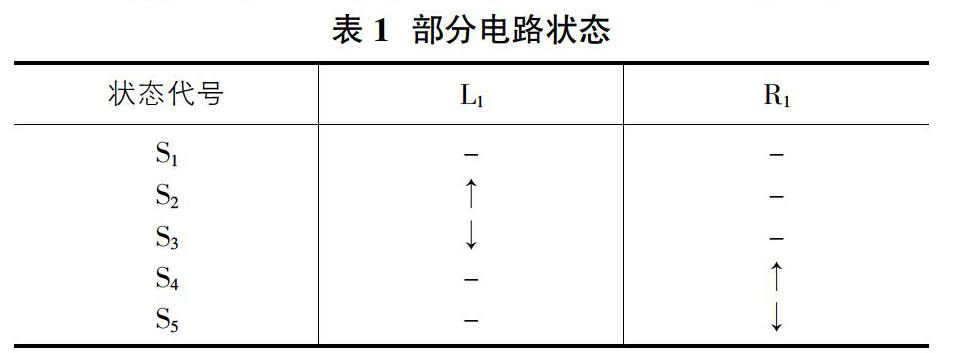
为了验证上述方法的有效性，以较为简单的某开关电源作为仿真验证对象，电路图如图1所示。电路中元件故障状态设定为标称值的正（↑）、负（↓）20%，节点OUT为输出测试点。仿真平台Orcad CIS 7.0和Matlab 8.5，采样点数1024。取电路状态集合如表1所示。当输入激励信号设定为时，对电路不同故障状态进行盒维数值计算。更进一步地，调整数值，考察不同频率下输出信号盒维数值变化趋势，结果如表2、表3及表4所示。

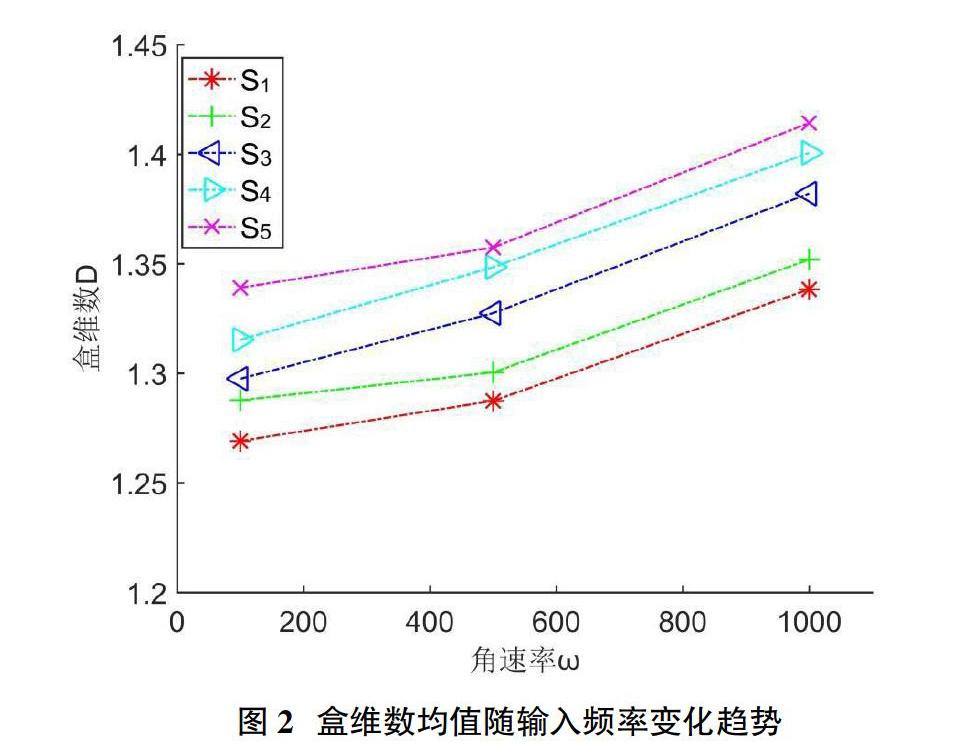
可以看出，对于同一输入频率，不同电路状态下的测试点输出信号分形维数是不同的。因此，利用分形维数进行电路故障特征识别进而进行故障诊断的方法是可行的。为了更进一步说明方法有效性，考察分形维数D随输入频率变化趋势，结果如图2所示。在输入信号频率相同的情况下，不同的故障状态对应着不同的盒维数值，说明各状态的分形特征是不同的;随着频率的增加，各故障状态盒维数值均有所增加，这是因为在采样参数不变的情况下，输出信号会显得更为复杂，也就是说其“填充空间的能力[6]”增加了。

虽然在该算例中，各故障状态在不同输入频率下分形维数同时升高，均值并未出现交叉混叠的现象。但是，由于每个单独的样本盒维数值围绕中心值上下波动较大，导致了其部分样本数据存在如图3所示的混叠现象。导致此种现象产生的原因是由于盒维数计算误差所致。图中明显可以看出，正是由于在频率为500Hz处S5状态下部分样本数据发生了较大偏差，导致其与S4状态发生了混叠。通过更进一步的研究发现，在面对更加复杂的装备模拟电路时，这种现象将会变得更为严重，导致该方法误差较大甚至完全失效。

3  建模效果分析

目前，模拟电路故障诊断方法多以时频分析为主。本文基于分形盒维数算法的故障诊断方法是以输出信号的分形维数为特征样本，考量的是其非线性特性、填充空间能力，是从另一个角度对故障特征的一种提取，是对传统方法一次有益的扩充。通过将模拟电路故障状态划分为不同的数值区间，被测电路输出信号与其进行对比后即可进行状态判定。基于盒维数算法的诊断方法以数值的形式判断电路故障状态，描述起来更加简单直观，其可操作性及直观性大大由于传统的故障诊断方法。并且此方法仅需要少量的先验样本即可完成对诊断系统的训练。因此，该算法在模拟电路故障诊断方面具有一定优势。然而，虽然基于盒维数算法的模拟电路故障诊断方法可以简单直观地进行故障状态判别，但仍存在许多方面不足：

①由于盒维数算法受自身定义限制，在无标度区及记盒数量影响下，其数值具有一定波动性。主要体现在：受仪器精度限制及无标度区影响，不同故障信号存在个体差异;受采样参数及噪声影响，相同故障信号盒维数值会略有差异。这一现象将对该方法的实际应用造成一定影响。

②该方法虽然不需要大量的先验数据，但是必须克服上述波动因素的影响，本章的做法是观察其平均值趋于稳定，而其样本数量已超过100个。

③与传统算法相同的是，该方法也需要对故障信号的整个波动状态范围进行全覆盖，因此，采样参数的选择也需要人为进行掌控。

④该方法所反映的是故障信号整体的分形特征，但仅仅是在一个测度上，并不能全面体现信号的局部特征，为此导致的混叠现象对故障诊断是极为不利的。

4  结束语

分形理论的应用范围十分广泛，将其作为一种信号处理的有力工具，应用于模拟电路故障特征提取有其明显的优势。但是，分形维数归根结底仅仅是在被测信号众多特征之中取出的一种，仅凭这一种特征无法对信号做到更加准确的刻画。因此，仅仅依靠分形维数一种手段解决本文所要研究的问题是不够的，还需将故障信号做进一步处理，比如利用多重分形对其进行扩维。

参考文献：

[1]Liangliang Zhang， Yuanhua Jia. The Arrival Passenger Flow Short-Term Forecasting of Urban Rail Transit Based on the Fractal Theory[M]. Springer Berlin Heidelberg， 2014.

[2]MichaelFrame， AmeliaUrry. Fractal Worlds[M]. Yale University Press： 2019.

[3]侯榮涛，朱飞.分形理论及其意义[J].信息与电脑（理论版），2011（01）：196.

[4]Rama Cont. Fractals in Engineering[M]. Springer London：2005.

[5]孙霞.分形原理及应用[M].北京：中国科学技术大学出版社，2003.

[6]Yu. V. Gulyaev， A. A. Potapov. Application of Fractal Theory， Fractional Operators， Textures， Scaling Effects， and Nonlinear Dynamics Methods in the Synthesis of New Information Technologies in Radio Electronics [J]. Springer journal， 2019， 64（9）.