农林牧渔行业CAPM模型有效性检验
林 纯
(四川大学 四川 成都 610000)
一、引言
农林牧渔业是民生之基,民生之本。当前,我国“三农”领域内仍存在许多重大难题,而这些难题也是党自十九大以来出台的各种政策所要攻克的对象。尤其在2018年至2020年初的这段时间,受到非洲猪瘟和新型冠状病毒疫情的影响,国内母猪产能大幅度下滑,生猪供给缺口仍然较大,连带其他种植业、畜禽养殖、饲料动保等子行业受到影响,给整个行业稳定有序的生产发展带来了重大的挑战。针对这一严峻形势政府在2020年2月5日出台的《2020年中央一号文件》中指出,要保障农产品的有效供给稳定农业生产。而在稳生产的过程中农业上市公司则起着领头的重要作用。因此,作为农业生产的重要一环,我们有必要对农业上市公司的股票收益率进行分析。
二、文献综述
在CAPM模型建立不久后,许多学者相继对其适用性及有效性进行检验。总体来说,检验结果分为两大派,一部分学者的实证结果支持CAPM模型的基本结论,而另一部分学者则发现利用CAPM模型对股票收益率进行解释还不够充分。
在支持CAPM模型的研究方面,John Lintner(1965)和Jan Mossin(1966)发现股票收益率与回归系数呈现正相关关系,并且还对Sharp所提出的模型进行了一定的修正和完善。Fama and MacBeth(1973)采用横截面的检验方法,以美国股票为研究对象,以1935年-1972年为研究区间,证明股票收益率与市场风险所代表的系统性风险存在正相关关系,符合CAPM模型的基本结论。相应的,我国学者也将CAPM模型用于我国金融市场,并对其有效性进行检验。朱宝宪和何治国(2002)以1995年前在沪深上市的公司为研究对象,发现股票收益率与系数呈正相关。吴世农和许年行(2004)以1995年2月至2002年6月在沪深两市上市的A股为研究对象,通过三维分组对CAPM模型进行实证检验,他们发现该模型的拟合优度在55.6%-92.5%之间,平均值约为79.4%,也就是说,市场因素能在很大程度上对股票收益率进行解释。国内学者不仅以股市整体作为研究对象,还分行业检验CAPM模型的有效性。陈倩(2019)以银行业为研究重点,通过利用日数据进行实证发现CAPM模型适用于银行业。张燕和王一登(2019)则以A股市场证券业为研究对象,考察了8个牛熊市周期中系统性风险和总风险的变化。经过实证发现CAPM模型适用于证券业,并且模型在熊市的拟合度高于牛市的拟合度。
相比于支持CAPM模型的研究,实证结果发现CAPM模型存在瑕疵的研究更多。Lakonishok and Shapiro(1986)发现在70年代后股票收益率和贝塔之间的正相关关系消失了。不仅在国外,我国也有学者发现类似的现象。丁琳和刘文俊(2013)探讨了上海证券交易所678只股票的平均超额收益率和系数之间的关系,并通过动态分组的方法来验证资本资产定价模型。他们发现虽然股票收益率和贝塔系数之间有线性关系,但是其斜率却是显著为负的并且截距项显著大于零。不仅正相关关系受到质疑,整个模型的有效性也有研究将其推翻。陈小悦和孙爱军(2000)采用分组识别法和截面回归法对中国A股和B股验证传统的资本资产定价模型,结果发现贝塔对中国股市股票收益率不具备解释能力,并以此否定该模型在中国的有效性。更进一步在行业层面,陈梦媛(2019)参考FM横截面检验方法,以房地产行业为研究对象,探讨2015年至2017年连续上市的股票的在CAPM模型的适用情况,经研究发现该模型不适用于房地产行业,她认为可能的原因是在样本期间内相关政策的频繁发布及变化影响了其适用性。总体来说,我国大部分学者认为CAPM模型在我国的适用性不强的原因在于我国股市起步较晚,金融市场发展不够成熟,仍然存在信息不完善、信息不对称等重大问题,从而使得我国市场不够有效。
三、研究设计
(一)样本选择
本文将针对农林牧渔行业验证CAPM模型的有效性,并通过参照Fama French和MacBeth的横截面检验方法展开。根据证监会2012年对行业的分类,农林牧渔行业共 47家上市公司。考虑到ST股票可能有财务状况或其它状况异常的情形,在停牌期间其股价会一直保持不变,不利于计算股票回报率,因此本文剔除了8只ST股票。同时,在剩下的股票中,由于太湖股份的股价异常,在较长的时间段内一直保持1元,本文也将其剔除。立华股份在2019年2月份上市,不符合本文的研究时间段,因此也将其剔除。最终,本文将以剩余的37只股票作为研究对象并以2017年—2019年作为研究区间采用Stata统计软件对该行业股票的日数据展开验证,其中数据来源于Wind数据库和CSMAR数据库。
(二)实证方法及变量说明
鉴于研究区间为2017年-2019年,因此本文将其根据年份划分为三个研究阶段,分别是2017年、2018年及2019年。在第一阶段即2017年初至2017年末,本文将利用市场模型,估计出每一只股票的系统性风险度量值,并将由小至大按照升序排列。同时根据的排序将其划分为6组,由于研究对象为37只股票,因此本文将多余的一只股票划分至最后一组,即值最高的一组有7只股票,其余组均为6只股票。根据市场模型,本文将以沪深300指数作为市场的代表计算市场收益率。其中,市场收益率与个股收益率均按照[(今日股价—昨日股价)/昨日股价]计算,具体计算公式如下:
(1)
Ri,t=αi+βi*Rm,t+εi,t
(2)
在第二阶段即2018年初至2018年末,根据第一阶段的分组结果,构建面板数据,同时再一次利用市场模型分别计算得出每一组的βp,计算公式如下:
Rp,t=αp+βp*Rm,t+εp,t
(3)
在第三阶段即2019年初至2019年末,将第二阶段所得出的βp以及残差εp,t的标准差代入以下模型来验证CAPM模型的有效性。其中无风险收益率Rf选取的是一年期定期整存整取利率,由于2017年—2019年没有发生变化,因此将其折合为日利率即为0.0041%在三年内一直保持不变。同时,第三阶段组合平均收益率按照市值加权得出。
Rp,t-Rf,t=α1+α2βp,t-1+θp,t
(4)
(5)
Rp,t-Rf,t=α1+α2βp,t-1+α3σp,t-1+θp,t
(6)
(7)
四、实证结果
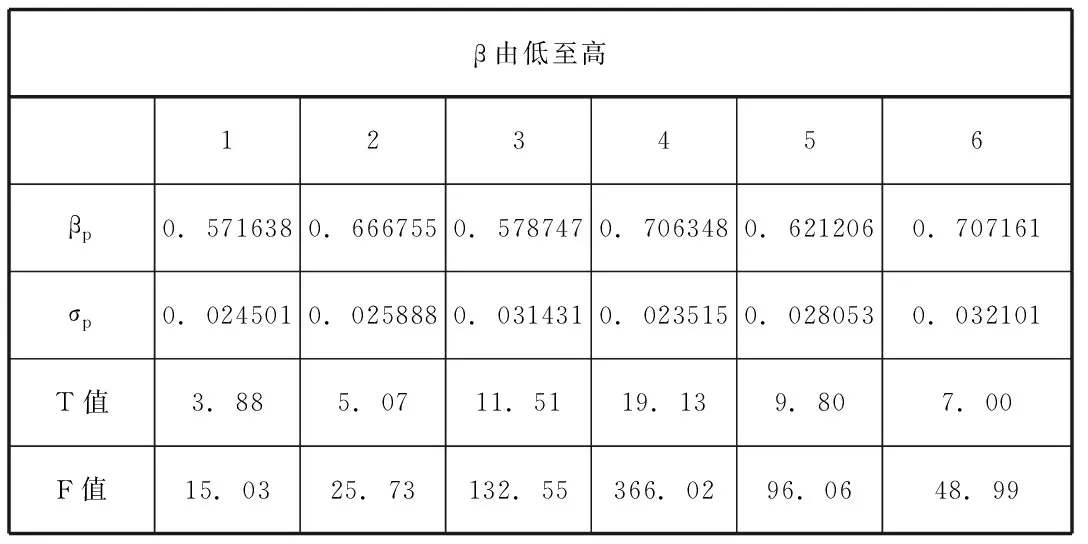
表1 第二阶段β分组情况
根据第二阶段回归结果可发现,每组的值均大于零,除去第一组在1%的水平不显著,在5%和10%的水平下显著,第二组至第四组均在1%的水平下显著。也就是说,市场风险在一定程度上能解释农林牧渔行业的股票收益率变动情况。同时,由上表可发现每组的值均小于1,这符合农林牧渔行业的特点,即存在一定的行业周期性,更大的程度上会受到自然环境的影响面对国家的宏观调控政策比如利率、汇率、通货膨胀政策,对金融或者房地产等行业的敏感度更大,而农林牧渔行业的敏感度相对较小,因此该行业的值相对较小。
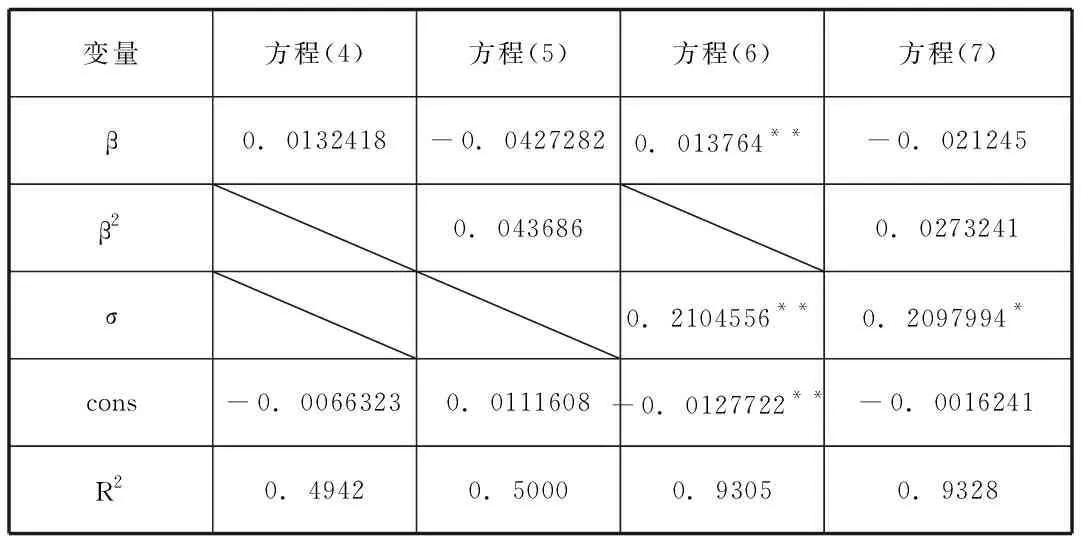
表2 第三阶段实证结果
根据上表可发现,拟合的最好的是方程(6),其β值显著异于零且大于零,说明农林牧渔行业风险与收益存在正相关关系,即风险越高收益越高,符合CAPM模型基本理论。鉴于σ是第二阶段所得出的残差的标准差,代表非系统性风险,并在在方程(6)显著异于零,说明系统性风险不能完全解释股票收益的变化,结合方程(4)(6)(7)可发现还存在一些有关公司特征的变量对股票收益率会产生影响,可能的原因是该样本容量较小,在第二阶段进行组合时非系统性风险没有得到充分分散。
总体来说,从方程(4)至方程(7)来看,农林牧渔行业其风险与收益之间不存在非线性的相关关系,但风险和收益存在正相关关系。并且,以β为代表的资产系统性风险不能完全解释该行业股票收益的变化,从加入解释变量后拟合优度R2来看,还存在一些非系统性对股票收益产生了较大的影响,也即CAPM模型在农林牧渔行业的适用性不强,其有效性不足。

