基于分布式内点法的输配协同优化调度
林敏洪, 侯祖锋, 王 超, 刘谋君, 许 桐, 郭 烨
(1. 广东电网有限责任公司 珠海供电局, 广东 珠海 519008; 2. 清华大学 深圳研究生院, 广东 深圳518055)
0 引言
可再生能源是分布式能源的重要组成部分,但可再生能源因其随机性、波动性以及不确定性,为电网运行带来了潜在风险。 分布式电源(Distribution Generation,DG),特别是光伏发电等可再生能源广泛接入配电网[1],使电网运行模式更为多样,因此,须要更为有效的方法实现对可再生能源的消纳。同时,输电网和配电网之间的互动也日益密切, 配电网的运行方式转变也将影响输电网的运行, 这势必对传统的输配分离管理模式造成挑战[2]。 基于输、配电网的天然耦合特性,若能实现输配两级网之间的有效协同, 则整个系统运行的安全性和经济性都将得到显著提升[3]。
目前输电运营商 (Transmission System Operator,TSO)和配电运营商(Distribution System Operator,DSO)相互独立,无法形成有效的联动。集中式输配联合调度策略需要采集全网模型和数据,根据模型拼接完成联合计算,但随着配电网主动资源的增多, 集中式计算无法满足大规模优化问题求解需求。 同时,DSO 和TSO 分属不同利益主体,现实中也无法完全共享关键信息[4]。
分布式优化方法仅须交换少量边界信息,即可以完成不同主体间全局优化问题的求解[5],因此,在输配协同调度中逐步受到学者们的关注。文献[6]提出了一种“异质分解”方法,利用输电网和配电网的物理特性, 两级电网分别交互不同类别的物理量, 解决输配协同机构及调度问题。 文献[7]进一步建立了广义主从分裂方法,适用于输配协同系统中的潮流计算、电压稳定、经济调度和最优潮流等多个应用场景。 文献[8]基于目标级联法, 提出了考虑高比例可再生能源接入的输配协同分层分级调控策略。 文献[9]基于并行子空间算法构建输配两级电网近似模型, 利用分解协调的调度策略,避免输配网间频繁的信息交互,但结果为近似解。 以上研究采用梯度类迭代求解策略或采取近似等值策略,实现快速求取全局次优解,但迭代次数对输电网和配电网间的通信成本以及联合问题的计算效率有着重要影响, 全局最优策略同时能够确保调度成本最小。所以,对既具有较少迭代次数, 又能获得和集中式方法一致全局最优解的输配分布式联合优化策略, 需要进一步深入的研究。
针对输配协同联合优化的迫切需求和基于研究现状, 本文提出一种基于分布式内点法的输配协同优化调度策略, 能够在保证和集中联合优化结果一致的情况下完成快速的分布式迭代优化。该策略利用内点法牛顿迭代的二次局部收敛性减少TSO 和DSO 间通信次数, 提高计算效率。 同时,基于矩阵分裂技术实现问题的分布式求解,保护TSO 和DSO 各自的信息隐私, 完成优化问题的本地分解计算。 仿真算例结果验证了本文所提输配协同分布式调度策略的准确性、 经济性和收敛性。
1 输配协同动态经济调度模型
在本文研究的输配协同动态经济调度模型中,定义输电网节点集合Ntrans和支路集合εtrans,配电网n 节点集合Ndist,n和支路集合εdist,n。
1.1 目标函数

式中:K 为动态经济调度的总时段数;gtrans为输电网发电机组集合;am,bm,cm分别为机组发电耗量成本系数;RU,m,t,RD,m,t分别为机组在t 时刻正备用和负备用;pU,m,pD,m分别为机组正备用和负备用价格;Ptrans,g,m,t为机组在时刻t 有功出力;pn,t为 配电网n 与输电网边界在时刻t 的电价;Pdist,n,t为配电网n 在时刻t 向输电网购买的有功功率;Qdist为配电网集合。
配电网n 经济调度优化目标由DG 发电成本CDG,n和购电成本CPT,n组成,即:

本文DG 为微型燃气轮机和分布式屋顶光伏发电设备。 微型燃气轮机成本函数形式和CTG相同。 对于分布式光伏发电,目标函数为弃光惩罚,即:
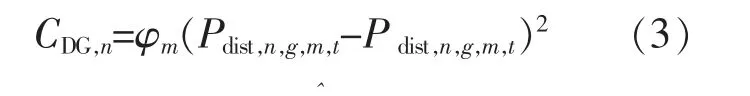
式中:φm为弃光惩罚系数;Pdist,n,g,m,t为预测光伏出力, 假设光伏设备运行在最大功率跟踪点模式(Maximum Power Point Tracking,MPPT)。
1.2 功率平衡约束
输电网采用直流潮流模型[8],[10],仅考虑有功功率平衡,其表达式为

式中:Dtrans为输电网负荷节点集合;Ptrans,i,d,t为输电网节点i 在时刻t 的预测负荷, 即输电网的总发电功率等于输电网的总负荷与输电网向配电网输送的总功率之和。式(4)反映了输电网和配电网边界联络线耦合关系。
与输电网不同, 主动配电网中存在众多分布式发电机,同时线路电阻较大,运行时网络损耗不能忽略,配电网采用文献[11]中基于一阶泰勒展开配电网线性化潮流方法,即:

式中:Pdist,n,iu,t,Pdist,n,ji,t分别 为 配 电 网n 中t 时 刻 节点i 流向节点u 和节点j 流向节点i 的有功功率; ~Pdist,n,ji,t, ~Qdist,n,ji,t为t 时 刻 节 点j 流 向 节 点i历史潮流; ~Vdist,n,j,t为t 时刻节点j 的历史运行电 压;rdist,nji为(i,j)支 路 电 阻;Pdist,n,d,i,t为t 时 刻 负荷 预 测 值;Pdist,n,g,m,t为DG 在 时 刻t 的 有 功 出 力;gdist,n为DG 集 合;i∈Btrans为 配 电 网 与 输 电 网 连 接的边界节点。
1.3 安全运行约束
对于满足系统安全运行的线路潮流约束、联络线功率约束和旋转备用约束在文献[9]中已有详细叙述。
1.4 发电机出力约束
对于输电网, 常规发电机组受到爬坡约束限制,有功出力无法在时刻间大幅变动,即:


1.5 输配协同优化调度模型
将上文变量整理为输电网变量xtrans和配电网变量xdist,n两类。 因输电网和配电网潮流平衡约束均为仿射形式,故式(4),(5)整合为Ax=b 形式,然后输配协同动态经济调度模型抽象为紧凑形式,即:

式中:A为常数矩阵;b 为常数向量;x={xtrans,xdist,n|n∈Qdist};g(x)=[gtrans(x),gdist,n(x)]T为输配联合调度模型中各项不等式约束;(·)T为转置;v 和λ 分别对应等式和不等式约束拉格朗日乘子。
2 分布式内点法
2.1 原对偶内点法

因牛顿法超线性收敛性质, 其迭代可在少量次数内高效完成,求得最终解为

式中:dk为搜索步长通过回溯线搜索方法确定[12]。
2.2 矩阵分解
Y 中H-1为对角矩阵,AAT代表输配一体网络中节点间的连接关系, 故Y 为稀疏对称矩阵,如图1 所示。 对于一个连接两配电系统的输电系统矩阵稀疏性, 输配电网间耦合菱形元素仅涉及联络母线的相关节点,具有可解耦性。

图1 Y 矩阵稀疏示意图Fig.1 Sparsity schematic of Y


2.3 收敛准则

3 分布式输配协同动态经济调度
设输电网节点i 与配电网n 节点j 为边界节点, 利用分布式内点法,TSO,DSO 优化求解流程如图2 所示。

图2 分布式输配协同经济调度流程图Fig.2 Distributed transmission distribution coordination economic dispatch procedure
由图2 可知,TSO,DSO 既能保护各自主体隐私,同时也极大提高计算效率。
4 仿真及结果分析
本文算例采用文献[10]的24 节点输电网和33 节点配电网系统,其结构如图3 所示。

图3 算例系统Fig.3 Test system
输电网的节点3 和节点19 分别和两个配电网连接。 其中,配电网的DG 配置参考文献[11]的算例系统,同时,为设计两个不同DG 接入配置的配电网,本文对一些DG 接入节点做了微调,选取文献[11]中算例系统中接入节点的邻近节点作为新DG 接入节点。配电网1 中配置17 节点为常规发电DG,21 和32 节点为分布式光伏发电设备,配电网2 中配置14 和26 节点为常规发电DG,22 和33 节点为分布式光伏发电设备。
仿真场景为以1 h 为间隔的全天日前调度,负荷和光伏预测出力标幺值曲线如图4 所示。

图4 负荷和光伏预测值曲线Fig.4 Load profiles and PV predictions
图中配电网1 的负荷占系统总负荷的15%,配电网2 的负荷占系统总负荷的35%,基于Matlab 验证所提出的分布式输配协同动态经济调度算法。
4.1 结果准确性验证
基于同一输配协同模型, 将分布式方法和集中式方法进行对比分析,结果如表1 所示。

表1 集中式和分布式计算结果对比Table 1 Comparison between centralized and distributed methods
由表1 可知, 分布式输配协同动态经济调度结果和集中式输配协同动态经济调度几乎一致。以集中式调度结果为基准, 输配协同分布式调度的总成本误差仅为0.027%,分布式策略能够取得和集中式策略相同的结果, 保证了所提方法的准确性。同时,由于循环终止准则造成的误差在可接受范围内。 本文所提分布式方法中分解计算的核心在于基于矩阵分裂技术完成对Y 矩阵的计算,其余计算步骤与集中式方法一致, 使得最终分布式和集中式方法从原理上分析应为同一结果。
4.2 经济效益对比
为体现输电网和配电网的协同经济调度的经济优越性, 将协同调度策略和传统的输电网配电网分离调度进行对比。 对于输电网配电网分离调度,在配电网侧,将输电网视作主动电源,起着传统调度中供能的作用。在输电网侧,将配电网看作被动负荷,其值为配电网负荷扣除DG 容量总额。输配分离调度中, 输电网和配电网基于上述假设分别独立计算各自内部的调度计划结果, 在实际运行中输配边界处会出现失配不平衡量, 影响实际调度效率,不能完全利用输配网的优势资源。由表1 可以发现, 传统的输配分离调度无法得到联合模型的最优解, 输配协同调度结果成本明显更低,可以节省16 442 美元,资源利用效率更高,在实际运行中具有重要意义, 可以进一步利用配电网中的灵活性资源, 降低未来实时调度中系统发电不足的潜在风险, 避免边界联络线计划不平衡量超过系统可调范围,保障系统运行安全。 同时,选取15:00 典型时刻作为弃光对比, 该时刻光伏发电充分,但负荷较少容易出现弃光现象。由于目标函数中对光伏惩罚二次项的加入, 优化模型会优先降低弃光量, 在联合调度中可以发现弃光现象均未发生, 而输配分离调度则会出现一定程度的弃光现象。
4.3 收敛性质分析
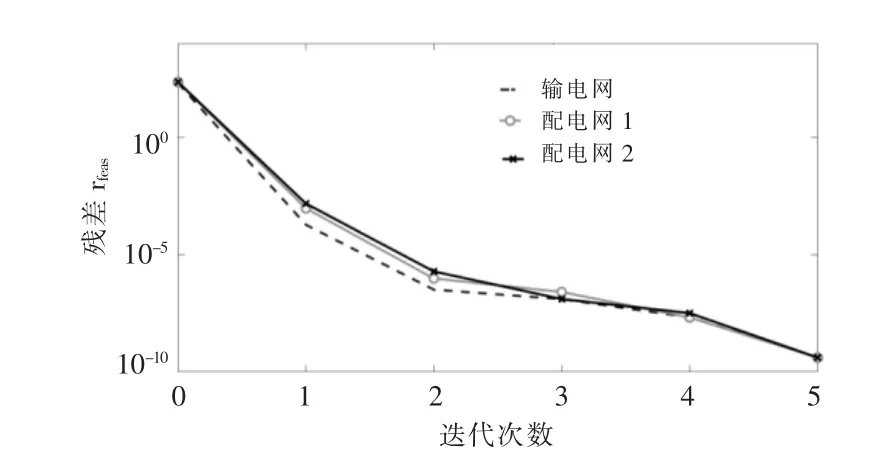
图5 分布式输配协同经济调度收敛图Fig.5 Distributed transmission distribution coordination economic dispatch convergence performance
为了进一步说明所提策略的优越性, 将本文所提方法与其他输配协同优化调度方法进行对比,如表2 所示。

表2 多种输配协同分布式方法对比Table 2 Comparison among various transmission distribution coordination distributed dispatch methods
由表2 可知,对比而言,文献[8]中基于目标级联ATC 法须要较高的迭代次数才得到与集中式方法一致的解。 文献[9]中改进CSSO 方法也须要较多次迭代才能收敛,同时只能求得近似解,精确度有待改善。 本文所提方法快于另外两种典型输配协同调度策略,收敛快速、调度结果准确,同时仅需要交互边界少量信息, 即可最大限度地保护TSO 和DSO 不同主体的隐私。
5 结论
本文针对传统输电网配电网分离调度造成的资源利用不充分、 输配联合优化信息隐私不受保护以及分布式优化通信成本较高的问题, 基于内点法和矩阵分裂技术, 提出了一种高效的输配协同联合优化调度策略。仿真算例分析表明,与传统输配分离方法相比, 该方法可有效调用输配两级电网资源,加强对可再生能源如光伏发电的消纳,降低系统总运行成本, 保障系统的运行安全。 同时,所提策略能够实现快速收敛,极大降低通信负担,主配网间仅需交换边界节点信息,不仅降低了通信负担更保证了不同运行主体内的信息隐私。随着坚强智能电网和泛在电力物联网的建设推进,各级网架之间的智慧耦合进一步深化,硬件建设将逐步完备, 合理高效的输配协同调度体系将会发挥更大作用, 有效调控主动配电网中渗透加深的可再生能源。

