基于分段随机FFT的干扰分析方法*

陈帅霖,陈 炜,吕 芳,刘 坤,刘满国，闫小东

(1 西安现代控制技术研究所, 西安 710065； 2 93811部队, 兰州 730000)

0 引言

现代战争已进入了电子战的时代，传统的以陆、海、空为主的战争已发展成为加入了天、电、网的“多维立体战”[1]。雷达对抗是电子战的研究热点[2]，面对各式各样的有源与无源干扰以及复杂的电子环境，根据所面临的干扰信号类型和特征，有针对性的选择相应的抗干扰措施，是雷达抗干扰技术的研究重点[3]。快速而准确的发现干扰并分析干扰信号的参数是雷达抗干扰的基础和前提[4]。

传统的干扰分析方法都需要从干扰信号的时域、频域或其他变换域提取特征。文献[5]对干扰信号的功率谱密度进行建模，提取了时变干扰相干时间和时变干扰相干带宽参数；文献[6]分析了卷积干扰形成的机理，提取了矩峰度系数等特征参数；文献[7]研究了弹载雷达对有源干扰的分析与识别方法。但若要在大带宽下分析频域特性并提取参数，运算量巨大，在某些特殊平台，如弹载平台，很难工程实现。

文中将结合相关课题，研究在有限资源的条件下，高效的对有源干扰信号进行分析的方法。通过低复杂度的算法流程，分析、提取干扰信号的多维特征，为后续的抗干扰措施打好基础。

1 干扰分析原理

重点研究有源干扰信号的参数分析。干扰种类有宽带压制、窄带瞄准、扫频。宽带压制分为连续型干扰和噪声型干扰；窄带瞄准分为欺骗式稀疏假目标和密集假目标；扫频干扰分为连续调频干扰和步进频脉冲干扰。所有干扰可以看作脉冲型、连续型、噪声型以及密集假目标等4种干扰在不同时间、频率上的组合。

假设我方雷达工作在S波段，跳频工作带宽为1 GHz，天线转速为6 r/min，脉冲重复频率为1 kHz，波束宽度为1°。敌方干扰源在固定方位对雷达进行干扰，雷达在机械扫描过程中接收干扰信号，进行分析。

1.1 干扰有无判断

雷达接收到的干扰信号可以分为两种情况，一种是大功率压制式干扰，可以直接用门限来判断是否有干扰；另一种情况是欺骗式干扰，干扰信号会淹没在噪声中，无法超过门限，需要用到某种自相关算法来提高干噪比，再进行判断。干扰有无的判断可分两步，首先用门限判断出压制式干扰，如果未检测到压制式干扰，再用自相关算法判断有无欺骗式干扰。在判断出干扰同时，可以得到干扰信号的起止时间和脉冲宽度。

1.1.1 双门限法

首先估计出无干扰情况下雷达的接收机底噪，并记录下来，作为门限标准。再设置门限为比底噪高3 dB。若有信号持续一段时间超过门限，则认为有干扰，反之则认为无干扰；同样，检测到干扰后，信号持续一段时间低于门限，则认为干扰结束。

具体方法为：在连续m个数据中若有n个超过门限，则检测到干扰，起始点为信号第一次过门限的时刻。干扰起始后，在连续m个数据中若有n个低于门限，则干扰结束，结束点为信号第一次低于门限的时刻。经过双门限判断，得到了干扰信号的起止时间，继而可得到干扰信号的脉宽。

1.1.2 滑动自相关法

较低干噪比(JNR)的情况下，门限法失效，而对信号做自相关运算，能够提高干噪比，增加检测概率，继而以较高的精度估计出干扰信号的起止时间[8]。假设接收信号x(n)为干扰与噪声的复合：

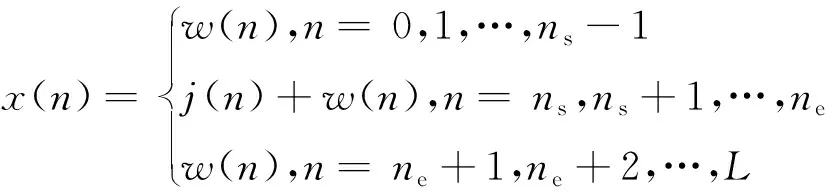
(1)

j(n)=Aexp{[j2πfcnΔt+φ(n)+θ0]}

(2)

其中，j(n)为干扰信号；A为信号幅度；fc为载频；Δt为采样间隔；φ(n)为调制相位；θ0为初相；w(n)为服从N(0,σ2)的复高斯白噪声。

对x(n)进行相关运算，得到其相关函数y(n)为：

(3)

通过化简可以得出如下的递推公式：

(4)

式(4)相当于对接收信号序列进行了窗长为L的滑动自相关，递推开始后只需进行增量计算，运算量很小，易于实时处理。经过自相关运算之后，相互独立的噪声被削弱，而干扰信号被加强，有利于干扰信号的检测。

1.2 干扰参数估计

1.2.1 起止时间与脉宽估计

由于干扰类型与干噪比未知，起止时间的估计需要结合双门限法与滑动自相关法等方法，步骤如下：

1)为了检测到噪声型干扰，首先用双门限法进行第一次检测，若干扰信号的干噪比较高，则可直接得到干扰信号的起止时间与脉宽；

2)找出接收信号的最大值，若最大值小于4倍门限值，则上一步估计出的起止时间与脉宽有误，需要进行滑动自相关(由于此时还未估计出起止时间，故不能计算信噪比，考虑到干扰叠加噪声的随机性，这里取4倍门限值作为判定标准)；

3)根据第2)步估计出的值来修正起止时间和脉宽。

1.2.2 干噪比估计

接收信号x(n)的二阶矩M2和四阶矩M4为：

(5)

由式(5)解得A2、σ2的估计值为：

(6)

可得干噪比估计值为：

(7)

工程实现时，二阶矩和四阶矩的估计可以采用接收序列的时间平均来近似[9]，二阶矩和四阶矩的近似表达式为：

(8)

式中N为接收信号序列的长度。

(9)

1.2.3 频率分析与雷达频点选择

将起止时间内的干扰信号变换至频域。先对功率谱进行平滑去除毛刺，有利于频率分析。令S(k)为平滑后的功率谱，找出S(k)的最大幅值S(k0)，再找出超过最大值一半的所有谱线，即可得到3 dB带宽。令k表示S(k)中所有大于0.5S(k0)的谱线的序号，则干扰信号带宽的估计值为：

(10)

中心频率的估计值为：

(11)

其中，Δf为频谱变换对应的频率分辨力。

经过上述频率分析，可以得到干扰信号所占据的频率范围，这些频点就是在雷达跳频带宽范围内对应的受干扰的频点。找出跳频工作带宽范围内远离这些干扰频点的数频点，即可作为雷达的最小受干扰频率。寻找最小受干扰频率的步骤为：

1)求取跳频工作带宽内每个未被干扰的频点到干扰频点边界的最小频率间隔；

2)找出第1)步求得频率间隔最大所对应的N个频点。

经过这两步，便得到了N个最小受干扰频率。

1.3 干扰分类

经过上述步骤的分析，得到了干扰信号的脉宽、中心频率、带宽及干噪比。可以根据这些信息对干扰信号进行分类。

首先，根据脉宽区分出脉冲型干扰，若估计出的干扰脉宽小于500 μs，则认为该干扰为脉冲型干扰。

其次，根据直接功率估计与矩估计方法得到的干噪比差异，区分出噪声型干扰。采用矩估计方法对噪声型干扰估计出的干噪比偏小，而对其他类型干扰的估计准确，可以根据这个差异来区分出噪声型干扰。

再次，根据时域与频域信息区分连续型干扰。当干扰信号的中频与带宽和窄带信息不同，则确定该干扰为连续型干扰。但如果估计出的干扰脉宽符合连续型干扰，并且估计出的中频与带宽和窄带信息一致，则需要进一步判断，该干扰可能是一连串脉冲型密集假目标干扰的叠加。

最后，确定该干扰是否为密集假目标。对符合上述特征的干扰信号进行脉冲压缩，依据两种干扰信号的特性，若脉压结果出现周期性的峰值，则干扰为密集假目标干扰；若无此特征，则为连续型干扰。

2 分段随机FFT

受到雷达信号处理系统硬件平台运算能力的限制，工程中对大脉宽信号做完整频谱分析很难实现，对参数未知的干扰信号做全频带分段FFT谱分析也不现实，例如脉宽500 μs的干扰信号，若采样率为1 GHz，该信号时域的点数为500 000点，若要进行完整连续的256点分段FFT谱分析，需要将近两千次的FFT运算，运算量巨大。

为了减轻处理负担，减少运算量，可以不做连续的谱分析，而以一定的时间间隔来做谱分析。设定总共做N次FFT，每次256点，不同的干扰信号脉宽对应不同的分析间隔。可以理解为，将脉宽内的干扰信号均匀分为了N段，只对每一段的前256点做FFT。假如脉宽内点数小于256×N，则依照实际的时域点数进行连续的分段FFT。分段FFT的原理示意图如图1所示。

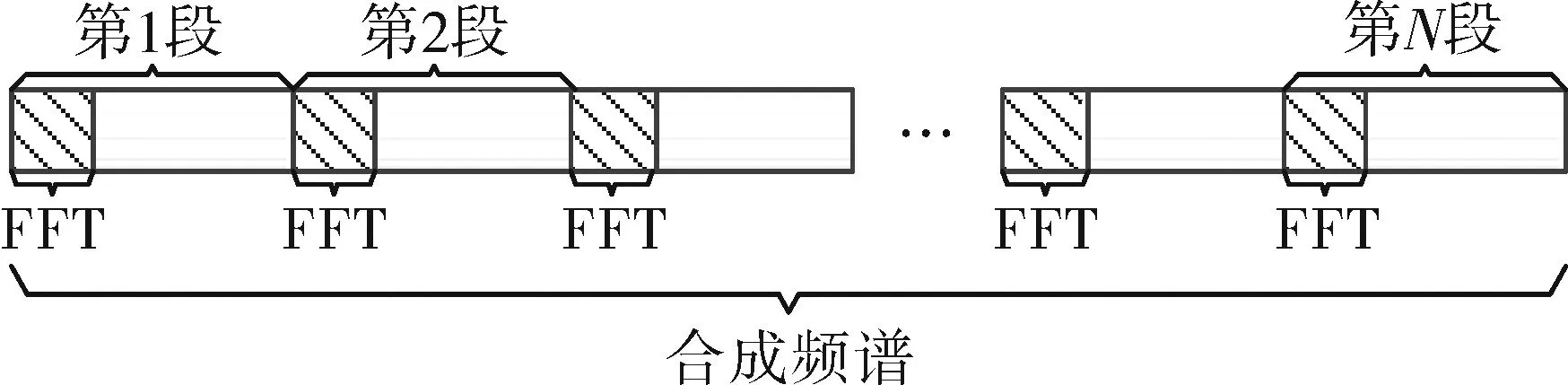
图1 分段FFT示意图

但是，当干扰为连续的密集假目标时，使用等间隔分段FFT方法进行谱分析，有可能谱分析的分段间隔与密集假目标干扰的重复周期“同步”，会造成总是重复的分析到子脉冲的同一频谱范围，使频谱损失掉一部分。这时可以采取间隔内“随机分析”，来避免这一现象的发生。即对干扰信号分段后，不是在每段数据的起始256点做FFT，而是在间隔内的数据中随机选取一点作为起始点做FFT，以便更“完整”的分析干扰信号的频谱。分段随机FFT的原理示意图如图2所示。

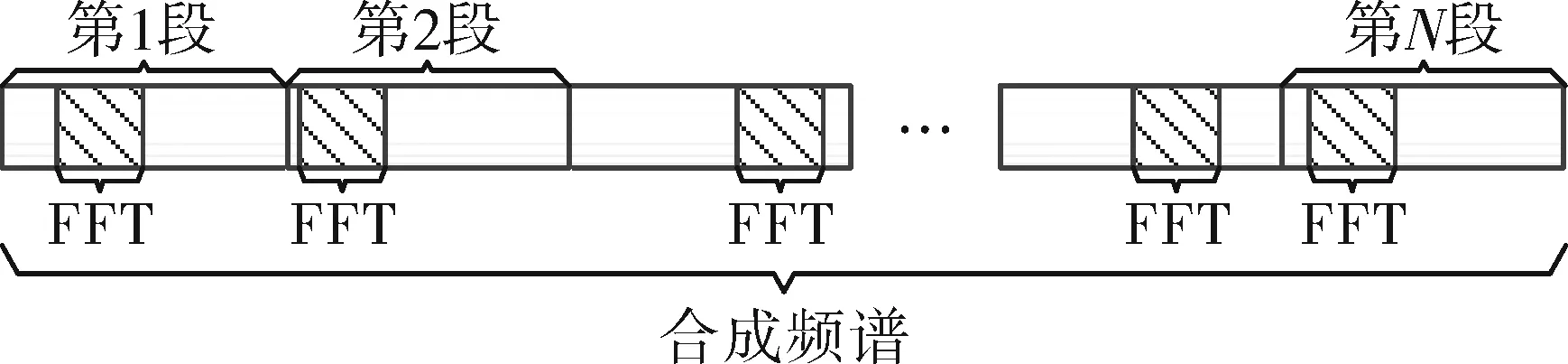
图2 分段随机FFT示意图

分段随机FFT的具体实现步骤为：

1)将待分析干扰信号均匀分为N段，计算段内点数(分段时若不能整除，可在分段前补零解决)；

2)在每段数据中随机选取一个起点，做256点FFT(需计算好点数，不能使FFT末端的点数超过分段长度)；

3)将N段FFT结果叠加起来，得到干扰信号的“完整”频谱；

4)采用1.2.3节中的方法进行中频与带宽估计。

下面分别对两种不同参数的密集假目标干扰信号进行传统分段FFT分析与40段的分段随机FFT分析。假设参数一为带宽40 MHz、脉宽80 μs；参数二为带宽70 MHz、脉宽55 μs。干扰由10个这样的脉冲信号连续拼接而成。两种谱分析方法的仿真结果如图3所示。

图3 谱分析结果

由图3(a)、图3(c)两图可以看出：对两种密集假目标干扰进行分段FFT谱分析，两个干扰信号频谱的右边都缺少一部分，估计出参数一干扰信号的中频为-10 MHz、带宽为24 MHz，参数二干扰信号的中频为-8 MHz、带宽为59 MHz，均出现了较大误差；对两个干扰信号进行分段随机FFT，由图3(b)、图3(d)两图可以看出：得到的频谱较为完整，估计出两个干扰信号的参数分别为中频-2 MHz、带宽40 MHz，中频0 MHz、带宽67 MHz，较为准确。

3 干扰分析方案

3.1 干扰分析步骤

根据上述干扰分析的原理与方法，对其进行整合，形成一套完整的干扰信号分析流程，详细步骤如下：

1)设置噪声门限，比接收机底噪大3 dB。若连续20个点的接收数据中有15个点过门限，则认为有干扰信号存在。

2)根据上一步的判断结果记录干扰信号的起始时间。干扰信号起始以后，若连续20个点的接收信号中有15个点低于门限，则认为干扰结束，记录下干扰信号的结束时间，并由此得到干扰信号的起止时间与脉宽。

3)估计干扰信号的功率及干噪比，并计算驻留时间内的干扰平均功率。

4)对起止范围内的干扰信号做分段随机FFT，计算干扰信号的功率谱，并对功率谱进行多点平滑，计算中心频率和带宽。

5)根据估计出的干扰信号中频和带宽，计算出最小受干扰频率。

6)根据干扰信号的脉宽判断出脉冲型干扰。根据矩估计与直接功率估计这两种干噪比估计的差异，判断出噪声型干扰。

7)根据窄带信息判断出确定的连续型干扰。

8)对不确定的干扰进行脉压，区分出连续型干扰和密集假目标干扰。

3.2 干扰分析流程图

完整的干扰分析流程图如图4所示。

图4 干扰分析流程

4 仿真验证

下面对脉冲型、连续型、噪声型和重叠密集假目标干扰进行试验仿真，以验证干扰参数分析与分类的正确性。

4.1 脉冲型干扰

模拟多种不同参数的脉冲型干扰，脉宽范围为2～500 μs，带宽范围为0～50 MHz，随机产生10种不同参数的脉冲型干扰，干噪比从4 dB变化到13 dB，每种干噪比进行100次蒙特卡洛实验，当估计的干扰参数与实际参数相符时认为分类正确。图5为脉冲型干扰识别概率。

图5 脉冲型干扰识别概率

经过多次仿真，可以看出本方法对脉冲型干扰的识别概率很高，参数提取准确。干噪比大于5 dB之后的识别概率已经接近1，干噪比较低时识别失败的原因主要是干扰脉宽的估计偏差，干噪比在4 dB时误差较大，干噪比超过5 dB之后最大的误差在0.15 μs左右。

4.2 连续型干扰

模拟多种不同参数的连续型干扰，脉宽范围为500～1 500 μs，带宽范围为30～1 000 MHz，随机产生10种不同参数的连续型干扰，干噪比从4 dB变化到13 dB，每种干噪比进行100次蒙特卡洛实验，当估计的干扰参数与实际参数相符时认为分类正确。图6为连续型干扰识别概率。

图6 连续型干扰识别概率

与脉冲型干扰相似，干噪比5 dB以上就能够准确识别。

4.3 噪声型干扰

模拟多种不同参数的噪声型干扰，脉宽范围为500～1 000 μs，带宽范围为100～1 000 MHz，随机产生10种不同参数的噪声型干扰，干噪比从4 dB变化到13 dB，每种干噪比进行100次蒙特卡洛实验。图7为噪声型干扰识别概率。

图7 噪声型干扰识别概率

图7中，蓝线表示估计频率与脉宽都准确时的识别概率，红线表示仅估计脉宽准确时的识别概率。由于噪声型干扰频谱较为杂乱，所以频率估计误差稍大，实验误差在8 MHz左右。仅考虑估计脉宽时的识别概率较高，干噪比6 dB以上识别准确。

4.4 密集假目标干扰

模拟不同干噪比情况下的密集假目标干扰，由于密集假目标干扰一般为转发式干扰，参数与雷达发射信号相同，所以仿真时只变换干噪比。干扰信号的干噪比从4 dB变化到13 dB，每种干噪比进行50次蒙特卡洛实验。图8为密集假目标干扰识别概率。

图8 密集假目标干扰识别概率

可以看出在干噪比大于5 dB时，该方法对叠加密集假目标干扰能够准确的识别，但方法中用到了脉冲压缩，计算量稍大。

5 结论

所提出的基于分段随机FFT干扰分析方法原理清晰、算法简明，考虑到一般硬件平台的运算能力，对算法进行了优化，易于实现。通过较低的运算量，解决了完整频谱分析运算量巨大、传统分段FFT方法频谱分析不完整的问题，并保证了干扰信号频率估计精度，适合通用雷达平台的工程实现。