利用海面温度和海面动力高度反演西太平洋月平均温度场

查国震，阮海林，梁建军，李 丽，吕海滨，成印河

(1.江苏海洋大学，江苏 连云港 222005； 2.自然资源部第三海洋研究所，福建 厦门 361005；3.中国科学院空天信息创新研究院，北京 100094)

海水三维温度场是海洋研究和海洋工程领域中最重要的数据资料之一。获取可靠的海水三维温度场有助于科研人员揭示海洋的三维结构及其变化规律。海水三维温度场也是海洋数值预报不可或缺的资料之一。目前获取海水三维温度场的方法主要有4种：通过温度链或者CTD进行现场观测的方法，因观测成本的限制，很难获得广阔大洋的三维温度场；声层析的方法同样成本高昂，且有不少技术问题亟待解决；利用海洋数值模式进行模拟的这类方法受到了国内外学者的重视，但存在精度不高的问题；利用卫星遥感资料反演这一类方法的缺点则是精度不高。

Argo海洋观测网的建立有效弥补了2 000 m以浅深度观测资料的匮乏，有助于为科学研究和工程应用提供可靠的数据资料。但Argo资料也存在一些缺陷：Argo浮标的平均布放距离是300 km，这使得Argo数据的空间分辨率较低，如果考虑到不同海区布放密度差异，某些海区的Argo资料非常稀疏；并且，Argo浮标是一种拉格朗日浮标，浮标空间位置不确定。以上原因导致基于Argo资料获得的三维温度场的空间分辨率也较低[1]。

卫星遥感技术的发展使得科研人员可以获取覆盖范围广、空间分辨率高、时间连续性强的海面温度和海面动力高度数据资料[2-5]。国内外学者给出了很多利用海面参数反演海水内部温度场的方法，这些方法主要分为3类。首先是基于动力学的方法，学者通常基于位势涡度守恒[6]，对海水进行绝热置换[7-8]，基于海面高度和次表层温盐关系、热成风关系等[9-10]，利用海面参数反演海水内部信息，这一类方法的物理意义清晰，但相关理论经过简化后难以反映复杂动力过程[11]。其次是基于变分法的方法，学者通常以温盐为控制变量，利用温盐场动力高度和海面动力高度之间的差异构造目标函数，进而反演海水内部温度场[12-15]。再次是基于统计学的方法，学者利用历史资料统计海面温度、海面动力高度和海水内部温度剖面之间的关系，然后利用卫星遥感资料反演海水内部温度场[16-23]。这类方法中，有的是基于经验正交分解，统计某些模态和海面参数之间的函数关系[24]，有的是基于耦合模态分析，找出温度和比容高度两个变量耦合模态振幅的函数关系，进而反演温度场[25]；正交函数分解法和耦合模态分析法的物理意义清晰，但均要求观测资料具有一定的时空连续性，当观测资料较少时，这两种方法的精度不高[11]。

在前人研究[26]的基础上，本研究基于量纲分析法获得了海面参数和海水内部温度剖面之间的函数关系，并给出了一种利用海面温度和海面动力高度反演大洋月平均三维温度场的方法。本研究首先基于最小二乘法确定方程中的待定系数，然后反演了西太平洋海域0～1 000 m深度范围月平均三维温度场，并将反演结果与基于Argo资料获得的三维温度场比较，二者具有较好的一致性。本研究旨在利用海面温度和海面动力高度估算海水内部的三维温度场，为海洋工程应用提供数据支持。

1 数据资料及其初步处理

本研究所用的卫星海面动力高度数据为法国Aviso卫星高度计数据中心提供的日平均海面动力高度(Maps of Absolute Dynamic Topography, MADT)数据产品。该数据产品融合了多颗卫星高度计数据，其空间分辨率为0.25°×0.25°(https://www.aviso.altimetry.fr/en/data/ products/sea-surface-height-products/global.html)。获得日平均海面动力高度资料之后，利用其计算月平均海面动力高度。

本研究所用的Argo资料为中国Argo实时资料中心提供的“全球Argo网格化产品”。该数据产品的Argo浮标资料来自于法国Argo数据中心。该网格化产品对数据的处理过程为：①对浮标剖面资料进行质控和温盐延时订正[27-28]；②对每个剖面剔除尖峰和毛刺；③利用时空加权平均技术对温盐剖面进行网格化处理；④基于Argo浮标资料，利用数据同化方法得到数据产品。该数据产品在0～2 000 m深度有26个标准层，其中1 000 m以浅有19个标准层，分别为0、10、20、30、50、75、100、125、150、200、250、300、400、500、600、700、800、900、1 000 m。该数据产品的时间分辨率为月平均，其水平空间分辨率为1°×1°(http://www.argo.org.cn/data/data1.html)。

为了评估本研究所述方法的有效性，选取西太平洋海域为反演海域。针对Argo温度场资料，截取经纬度范围为124.000°～140.000°E、15.000°～23.000°N之间的数据。针对卫星海面动力高度资料，截取经纬度范围为123.875°～140.125°E、14.875°～23.125°N之间的数据。

在水平空间，Argo数据格点和卫星海面动力高度数据格点存在空间位置不匹配的问题。如图1所示，在水平方向，Argo温度场的数据格点与海面动力高度的数据格点位置在经、纬度方向各出现了0.125°的差异。每个黄色区域内的4个蓝色点标出了与每个红色点最邻近的卫星海面动力高度数据格点。本研究利用每个黄色区域内的4个卫星海面动力高度数据计算出与红色点位置对应的卫星海面动力高度数据，计算的方法为将4个点取平均值。这样就得到了与每个Argo温度场数据格点对应的海面动力高度数据格点。

2 结果与讨论

2.1 反演模型

海水状态方程主要包括了4个参数，其表达式如下：

F[ρ,S,T,P]=0

(1)

式(1)中：ρ为密度(kg/m3)，S为盐度，T为温度(℃)，P为压强(Pa)。通过量纲分析得到下面的无量纲海水温度方程[26]：

(2)

(3)

为了利用方程(3)反演温度场，需要确定参数nz。对上式进行形式变换，得到

(4)

或者写为

(5)

得到关于参数nz的显式方程。

基于一个较大的海面温度、温度剖面和海面动力高度的样本空间，利用最小二乘法估计参数nz。为了方便叙述，取一些记号，记

(6)

(7)

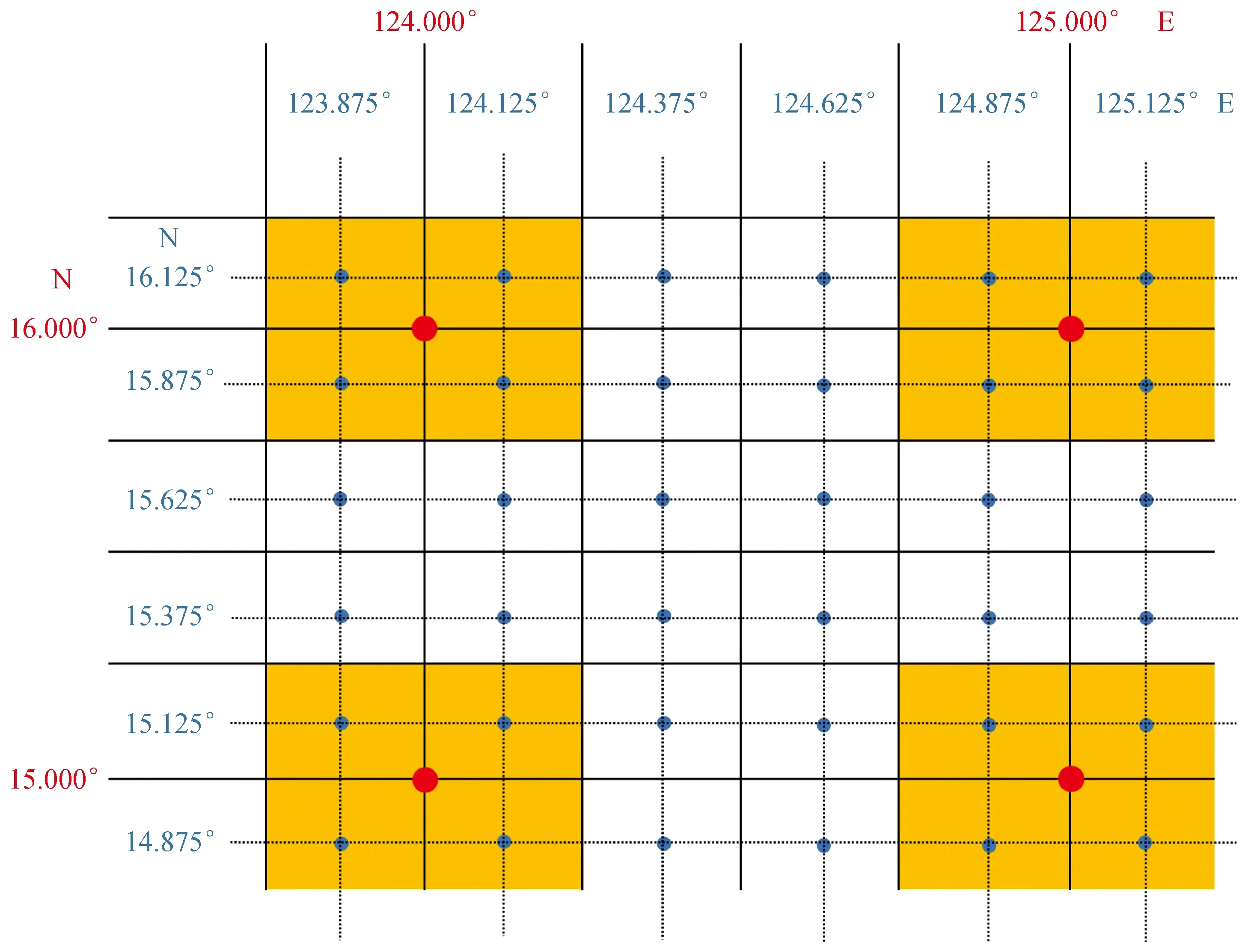
图1 Argo温度场和卫星海面动力高度数据水平空间格点位置示意Fig.1 Horizontal positions of the grids by Argo-based monthly-mean temperature field and dynamic sea surface height data红色点为Argo温度场数据格点位置，蓝色点为卫星海面动力高度数据格点位置；红色字标示Argo温度场格点的经纬度坐标，蓝色字标示卫星海面动力高度格点的经纬度坐标。

从而方程(4)变为

yz=-nz·xz

(8)

在每层深度z确定时，考虑

(9)

式(9)中：f为误差项，M为样本数，上标i为样本次序，考虑方程(9)关于参数nz的稳定点，得到

(10)

展开为

(11)

得到

(12)

最终得到

(13)

2.2 反演结果及误差评估

为了利用海面温度和海面动力高度估算研究区域内0～1 000 m深度范围月平均三维温度场，首先基于方程(13)估算参数nz。本研究利用2005年1月至2007年12月共36个月的月平均海面温度、海面动力高度和Argo温度场资料估算参数nz。考虑到数据的一致性，本研究将Argo温度场0 m处的温度作为海面温度。本研究所用海面动力高度为前文插值获得的月平均海面动力高度数据。

在反演区域内，Argo温度场在纬向有9个温度剖面，在经向有17个温度剖面，因而在整个反演区域有153个温度剖面。另外，Argo温度场在0～1 000 m深度有19层。在水平向，计算获得的nz剖面的位置和Argo温度场的剖面位置一致。反演区域内一共计算获得了153个nz的剖面。nz剖面层深也和Argo温度场的层深一致。由于反演温度场的表层温度直接等于海面温度，因而不需估算n0。图2(a、b)为估算的7月和12月每个水平格点位置的nz剖面。

图2 反演区域内7月和12月nz的剖面Fig.2 Profiles of parameter nz on the inversion area in July and December

获得nz的剖面之后，本研究利用2008年1月至2009年12月的月平均海面温度和海面动力高度反演了西太平洋海域0～1 000 m深度范围的月平均三维温度场，并将反演结果与对应时间和空间位置的Argo温度场进行了比较。作为示例，图3、4分别为2008年和2009年的3条反演的温度剖面和误差剖面。

图3 2008年反演区域内3个不同位置的温度剖面示例Fig.3 Temperatures on 3 different profiles in the inversion area of 2008(a-c)分别为1、7、10月的温度剖面，(d-f)分别为(a-c)对应的误差剖面。

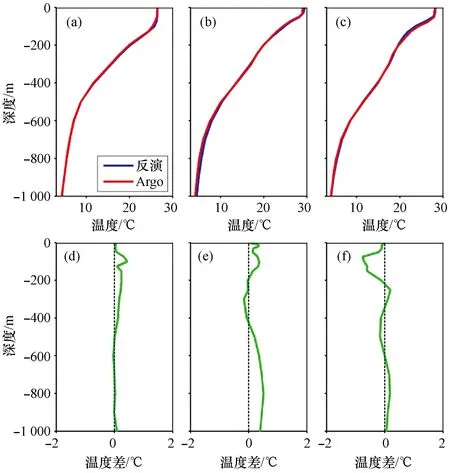
图4 2009年反演区域内3个不同位置的温度剖面示例Fig.4 Temperatures on 3 different profiles in the inversion area of 2009(a-c)分别为1、7、10月的温度剖面，(d-f)分别为(a-c)对应的误差剖面。

本研究将反演的温度场与Argo温度场进行比较，计算二者在对应时间、对应水平空间位置和对应深度的温度差，然后评估误差，其公式如下：

(14)

(15)

式(14、15)中：δ为平均误差(℃)，Ti为反演的温度(℃)，Ti′为观测的温度(℃)，σ为误差均方根(℃)，N为总样本数。

因海面温度不需反演，所以不参与误差估算。除去海面，反演的温度场共18层，水平空间共153个剖面，每年12个月，因而用于评估误差的2008年和2009年数据点个数均为33 048个，两年合计66 096个。计算的平均误差和误差均方根如表1所示。该方法估算的月平均温度场的平均误差为0.56 ℃，误差均方根为0.76 ℃。本研究还计算了除表层之外的各个深度的平均误差和误差均方根，获得了二者随深度变化的曲线，结果如图5所示。本方法的误差首先随深度增加而增加，但在400 m以深，误差随深度增加而减小，这可能与中层水月平均温度变化较小有关。

表1 平均误差及误差均方根

图5 平均误差和误差均方根随深度变化的曲线Fig.5 Curve profiles of mean error and root mean square error changes with depths

图6为统计的误差直方图，误差位于[0.0 ℃ 0.5 ℃]、(0.5 ℃ 1.0 ℃]和(1.0 ℃ 1.5 ℃]区间的数据点的占比分别为63.1%、22.8%和9.4%，误差大于1.5 ℃的占比为4.7%。以上计算结果表明，反演的月平均温度场具有较好的精度。

图6 误差直方图Fig.6 Error histograms

2.3 讨论

海洋内部有复杂的动力过程，不同时间和空间尺度的海洋和大气现象都可以影响海水三维温度场，例如洋流、中尺度涡、上升流、海洋内波和海面风剪切等。海面温度可视为海水三维温度场的边界条件，海面动力高度可从一定程度上反映海水内部的动力过程。本研究尝试以这两个参数为输入变量反演月平均海水三维温度场。通过将反演结果与中国Argo实时资料中心提供的全球Argo网格化产品的比较，证明该方法反演的月平均温度场具有较好的精度。在海洋研究和工程应用中，日平均温度场具有更重要的意义。与平均态的月平均温度场相比，日平均温度场的变化更加复杂。因为本研究推荐的反演模型仅仅考虑了两个参数的影响，所以是一个简化的模型。如果用其估算日平均温度场，会出现较大的误差，这一问题有待进一步探索。另外，上层海水直接受太阳辐射和海面风剪切等因素的影响，海洋中复杂的中尺度和次级中尺度海洋现象都会影响上层海水温度变化。与上层海水温度场相比，中层和深层温度场较稳定。实验结果表明，本研究推荐方法的误差在400 m以深随深度增加而减小，这和中层、深层水比较稳定有关。

3 结论

本研究利用量纲分析法获得了海面温度、海面动力高度和海水内部温度剖面之间的函数关系，进而提出了一种利用海面参数反演大洋月平均三维温度场的方法。基于2008年和2009年的海面温度和海面动力高度资料，本研究反演了西太平洋海域0～1 000 m深度范围的月平均三维温度场，并将反演结果与基于Argo资料获得的温度场进行比较。该方法反演的三维温度场的平均误差为0.56 ℃，误差均方根为0.76 ℃。此外，从本研究统计的误差直方图可知，其误差位于[0.0 ℃ 0.5 ℃]、(0.5 ℃ 1.0 ℃]和(1.0 ℃ 1.5 ℃]区间的数据点的占比分别为63.1%、22.8%和9.4%，误差大于1.5 ℃的占比为4.7%。结果表明，本研究提出的方法具有较好的精度。