波形钢腹板PC箱梁的等效计算方法

莫利君, 陈 华

(1.湖北省交通规划设计院股份有限公司, 湖北 武汉 430051; 2.湖北交投十巫高速公路有限公司, 湖北 十堰 442000)

波形钢腹板PC箱梁充分利用了混凝土抗压能力强和波形钢板抗剪能力强的特点，具有施工简便、梁体轻盈、预应力效率高、预应力可更换等优点。该桥型无腹板开裂问题，结构耐久性好，目前国内多座桥梁采用了该种结构形式[1]。

目前，波形钢腹板PC箱梁的计算大多采用有限元方法建立实体模型、梁单元建立组合材料模型。有限元模型建模复杂、单元数量多、计算时间长；组合材料模型建模中需考虑不同材料组合时参数取值的合理性和计算尺寸调整时模型修改的不便性。本文采用等效模型，将波形钢腹板等效为正交异性平板，然后利用正交异性平板来建立等效模型。将波形钢腹板等效为混凝土直腹板，采用与混凝土箱梁相同的计算方法，大大减小了计算工作量[2]。为了证明采用等效模型计算的有效性，本文以某波形钢腹板连续刚构桥为实例，将采用Midas Civil建立的整体模型和等效模型进行对比分析。

1 波形钢腹板纵向等效刚度

波形刚腹板箱梁中，波形钢腹板的纵向抗压刚度很小，因此承受的纵向压力和纵向弯矩均非常小。通过单位力法按刚度等效原则分别计算波形钢板的等效厚度和等效弹性模量，分别采用公式(1)和公式(2)进行计算[3]。

(1)

(2)

式中:a为直板段幅宽，mm；b为斜板段投影宽，mm；c为斜板段幅宽，mm；h为波高，mm；t为钢板厚度，mm；E为钢的弹性模量，N /mm2。

把波形钢腹板组合箱梁中与波形钢腹板纵向刚度相同的直钢腹板称为“等效直钢腹板”。等效直钢腹板既可以是厚度等效的直钢板，也可以是弹性模量等效的直钢板。为了便于分析，进一步把等效直钢腹板等效成混凝土直腹板。因此，式(1)可以改成：

(3)

式中:Ec为混凝土的弹性模量，N /mm2；tx为混凝土腹板的厚度，mm。

波形刚腹板采用纵向等效刚度的方式，将整体计算模型等效为混凝土直腹板的混凝土箱梁模型，从而使整体计算模型从钢板和混凝土组合材料的组合模型简化为常规的混凝土箱梁模型，简化了计算模型，提高了建模和计算效率。

2 工程实例

某波形钢腹板连续刚构桥，主桥跨径(57+100+57)m，主梁采用单箱单室截面，箱梁处根部梁高6.2m，边墩支点及跨中梁高3.0m，梁高按1.8次抛物线变化。箱梁顶板宽12.24m，底板宽6.5m；顶板厚0.3m，底板厚0.32～0.7m。波形钢腹板采用1600型波形钢板，材料为Q355NHD耐侯钢，采用无牵制模压法成形。钢腹板波形水平段长430mm，斜段长430mm，斜段水平方向长370mm，波高220mm，加工弯曲弯折半径不小于15 倍板厚。波形钢腹板的厚度分别为16、20、22mm。预应力体系采用体内预应力与体外预应力相结合的设置方式。体内纵向预应力采用12φs15.2mm、15φs15.2mm、17φs15.2mm、22φs15.2mm钢绞线，横向预应力采用3φs15.2mm钢绞线；体外预应力采用15φs15.2mm和22φs15.2mm钢绞线。主梁采用对称悬臂施工。

2.1 模型建立

1) 采用波形钢腹板截面建立模型。

采用Midas Civil自带的波形钢腹板截面建立主桥模型(下文简称实际模型)，波形钢腹板采用组合材料，模型断面和全桥模型分别如图1、图2所示。

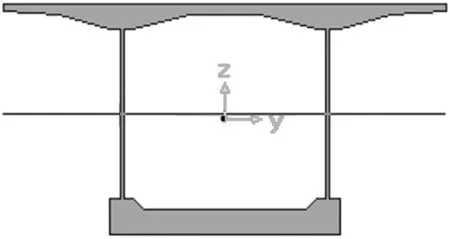
图1 实际模型的断面图

图2 实际模型的全桥有限元模型

2) 采用腹板纵向刚度等效建立等效模型。

根据波形钢腹板纵向刚度等效原理，将波形钢腹板等效为具有相同纵向刚度的混凝土直腹板，再按照全截面均为混凝土材料的要求建立有限元模型(下文简称等效模型)，其断面图和全桥模型分别如图3、图4所示。

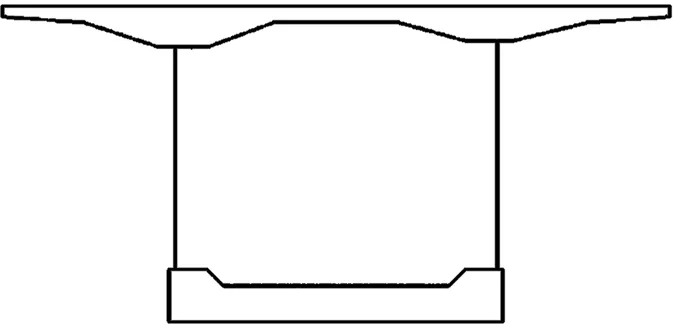
图3 等效模型的断面图

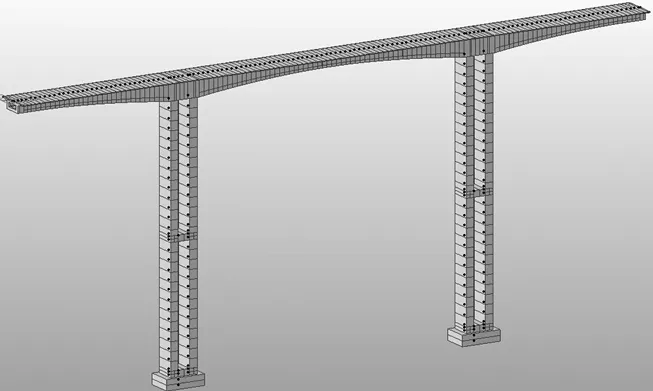
图4 等效模型的全桥有限元模型

2.2 纵向静力计算对比分析

1)顶、底板混凝土抗裂计算对比。

按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》6.3.1条第1款进行计算。实际模型和等效模型的顶板和底板的混凝土拉应力包络图如图5～8所示。

图5 实际模型顶板拉应力包络图(单位： MPa)

图6 实际模型底板拉应力包络图(单位： MPa)

图7 等效模型顶板拉应力包络图(单位： MPa)

图8 等效模型底板拉应力包络图(单位： MPa)

由图可知，实际模型顶板最大拉应力为1.1MPa，底板最大压应力为0.9MPa；等效模型顶板最大拉应力为1.1MPa，底板最大压应力为0.9MPa。等效模型计算的顶板和底板的拉应力与实际模型计算的结果相同。

2)顶、底板混凝土压应力验算对比。

按照JTG 3362-2018规范的7.1.5条第1款进行计算。实际模型和等效模型的顶板和底板的混凝土压应力包括图见图9～12。

图9 实际模型顶板最大压应力包络图(单位： MPa)

图10 等效模型顶板最大压应力包络图(单位： MPa)

图11 实际模型底板最大压应力包络图(单位： MPa)

图12 等效模型底板最大压应力包络图(单位： MPa)

由图可知，实际模型顶板最大压应力为17.9MPa，底板最大压应力为12.1MPa；等效模型顶板最大压应力为17.1MPa，底板最大压应力为11.5MPa。2个模型计算结果差异小于5%。

3)承载能力验算对比。

实际模型和等效模型抗弯承载能力验算见图13和图14。

图13 实际模型抗弯承载能力包络图(单位： kN·m)

图14 等效模型梁抗弯承载能力包络图(单位： kN·m)

由图可知，实际模型最大弯矩为38582.2kN·m，最小弯矩为-415329.7kN·m；等效模型最大弯矩为38921.8kN·m，最小弯矩为-419312.9kN·m。2个模型计算差异小于1%。

综上所述，采用等效模型计算波形钢腹板PC箱梁的正截面抗裂、抗压和抗弯承载能力均满足计算精度要求。

3 波形钢腹板验算

3.1 波形钢腹板的剪切验算

根据波形钢腹板等效模型的内力，按照波形钢腹板计算规范对波形钢腹板进行验算。

波形钢腹板PC箱梁桥的剪力全部由波形钢腹板承担，且剪应力沿腹板高度方向均匀分布，钢腹板的应力状态一般设为纯剪。因此，波形钢腹板PC箱梁桥的抗剪验算为对波形钢腹板剪应力强度进行校核，包括抗剪强度、局部屈曲强度、整体屈曲强度和组合屈曲强度4项校核内容。本文采用平均剪应力计算理论，对波形钢腹板进行设计和2种极限荷载状态下的抗剪强度校核。

3.1.1正常使用极限状态下的钢腹板剪应力验算

根据《波形钢腹板预应力混凝土组合箱梁桥设计与施工规程》(广东省地方标准)[4](下文简称广东标准)9.1.5条和9.1.7条进行计算。正常使用极限状态下波形钢腹板的剪应力的计算值与允许值如图15所示。

图15 正常使用极限状态钢腹板剪应力

由图可知，荷载标准值组合下，波形钢腹板的剪应力均小于Q355NHD耐侯钢的容许剪应力，最小安全系数为1.19，满足广东标准要求。

3.1.2承载能力极限状态下的钢腹板剪应力验算

根据广东标准，厚度16mm及16mm以下的Q345钢板抗剪设计值为160MPa；16～35mm的Q345钢板抗剪设计值为150MPa。根据广东标准9.1.6条验算波形钢腹板的承载能力极限状态抗剪强度，计算结果如图16所示。

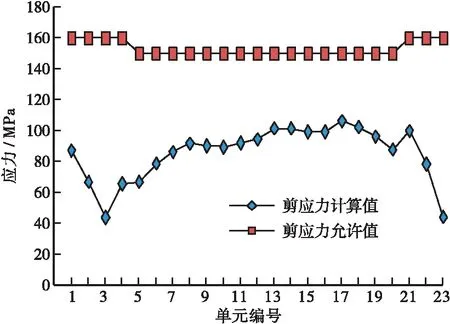
图16 承载能力极限状态钢腹板剪应力

由图可知，承载能力极限状态基本组合下，波形钢腹板剪应力均小于设计容许值，最小安全系数为1.48，满足广东标准要求。

3.2 波形钢腹板屈曲安全性验算

3.2.1局部屈曲验算

按照广东标准第9.1.9条进行波形钢腹板局部屈曲验算，计算结果如图17所示。

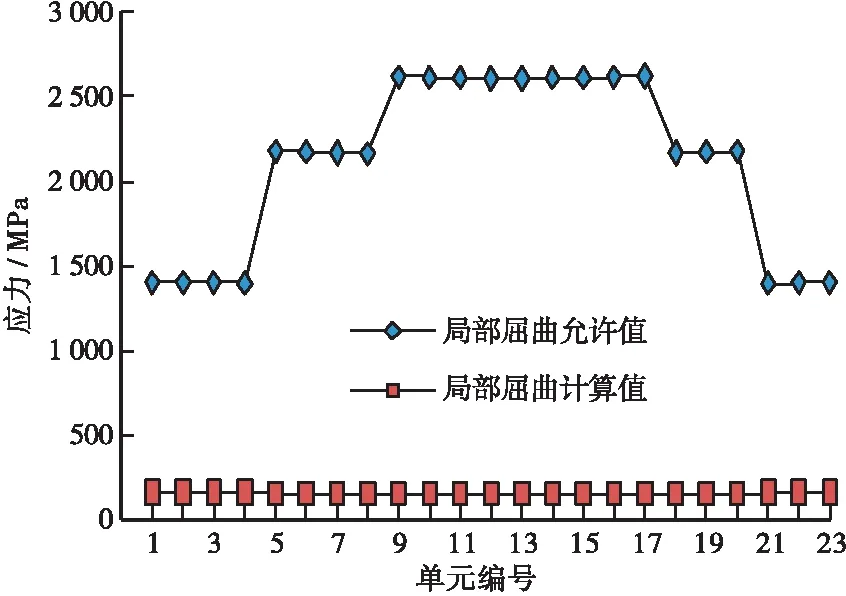
图17 波形钢腹板局部屈曲

由图可知，波形钢腹板最小局部屈曲临界强度为1400.366MPa，大于屈服剪应力的160MPa，波形钢腹板的局部屈曲验算满足规范要求。

3.2.2整体屈曲验算

按照广东标准中9.1.9条计算波形钢腹板弹性整体的屈曲临界剪应力，计算结果如图18所示。

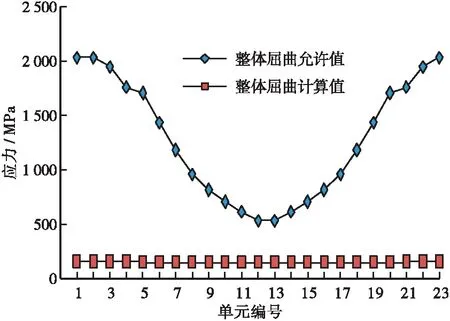
图18 波形钢腹板整体屈曲

由图可知,波形钢腹板最小整体屈曲临界强度为533.20MPa，大于屈服剪应力的150MPa，波形钢腹板的整体屈曲验算满足广东标准要求。

3.2.3组合屈曲验算

按照广东标准第9.1.8条验算波形钢腹板的组合屈曲，计算结果如图19所示。

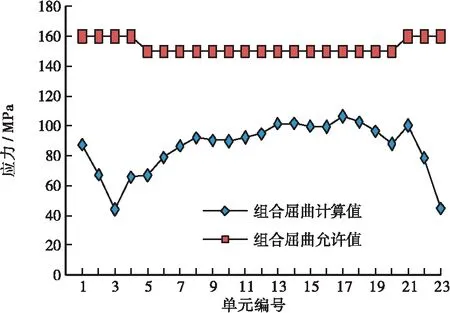
图19 波形钢腹板组合屈曲验算

由图可知，承载能力极限状态下，波形钢腹板的组合屈服强度最不利值为106MPa，小于组合屈曲临界剪应力的150MPa，最小安全系数为1.41，波形钢腹板的组合屈服验算满足广东标准要求。

4 结论

1) 波形刚腹板PC箱梁采用混凝土直腹板等效模型对箱梁的混凝土顶、底板的受力和变形进行计算，计算结果与实际模型的计算结果差异较小，误差均在5%以内。因此，可采用等效模型对混凝土顶、底板的受力和变形进行验算。

2) 采用等效模型能大大简化波形钢腹板混凝土箱梁的组合梁的计算工作量，简化计算，提高建模计算的效率。

3) 实际模型与等效模型均无法直接对波形钢腹板进行验算，需根据波形钢腹板的相关规范对波形钢腹板正常使用极限状态下的剪应力和承载能力极限状态下的剪应力、局部屈曲、整体屈曲和组合屈曲进行验算。