基于消费级无人机的模型构建精度研究

高 翔

（安徽理工大学测绘学院，安徽 淮南 232001）

1 摄影测量与消费级无人机的研究背景

近年来，随着我国地理信息行业的不断发展，数字城市、数字校园的建设也如火如荼。由于传统方法在大区域建模中存在效率低、速度慢等问题，航空摄影测量技术凭借着高效、快速的优点应运而生，使得大区域建模成为可能[1]。但是，传统航空摄影测量只能单角度获得像片信息，导致建立的三维模型存在遮挡、纹理信息不够完整等问题。针对这一问题，国内外学者进行了许多探索，并在航空摄影测量的基础上研究出一种新技术——倾斜摄影测量技术[2]。倾斜摄影测量技术利用同一传感器在不同角度获取像片，有效地解决了传统航空摄影测量单角度获取像片的问题。

目前，倾斜摄影测量技术通过在无人机上搭载传感器对目标物体进行多角度测量。无人机按照体积、用途可分为专业性无人机和消费级无人机，消费级无人机具有质量轻、成本低等优点[3]。

随着我国科技的不断发展，深圳市大疆创新科技有限公司（简称“大疆”） 等科技公司推出了“悟”“精灵”系列的消费级无人机产品，使用消费级无人机进行摄影测量变为可能。本文对其测区进行研究分析，并对消费级无人机建模精度进行验证，进而分析相对航飞高度、像控点对其建模精度的影响。

2 三维模型构建若干技术

2.1 畸变校正

消费级无人机因体积小、质量轻等原因，一般搭载的都是非专业型量测相机，也称为非量测相机，在制作、设计和安装过程中的误差会引起相机物镜畸变，使得像点偏离其理论位置，引起像点位移，导致在航拍过程中地物点、像点、摄影中心三点不位于同一条直线上[4]。因此，先对相机进行标定以获取相机镜头畸变参数，再根据以下模型进行相机镜头畸变校正，消除畸变误差。相机镜头畸变校正模型的表达式方程组为

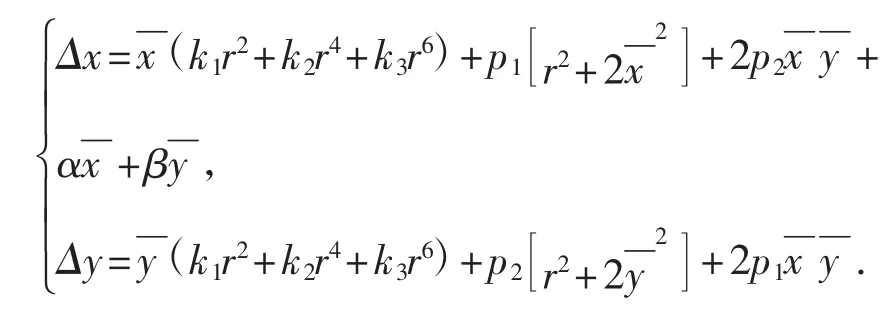
2.2 光束法空中三角测量

空中三角测量是通过在地面布设少量控制点，按照平差模型，求解出所有像片的外方位元素和地面未知点坐标的过程。空中三角测量按照平差模型分类可分为航带法、独立模型法和光束法，其中光束法平差结果最为严密[5]。

光束法将像点坐标作为观测值，首先获取所有像片的外方位元素和地面未知点坐标的近似值；其次，列间接平差方程求得所有像片的外方位元素改正值；最后，利用多张像片前方交会获取地面未知点坐标。

2.3 影像匹配

影像匹配是指在影像中寻找同名点的过程。随着数字摄影测量的发展，现阶段已使用计算机替代人工完成影像匹配。

影像匹配主要分为基于灰度的影像匹配和基于特征的影像匹配两种方式，其中基于特征的影像匹配被广泛用于摄影测量中。

尺度不变特征（Scale-Invariant Feature Transform，SIFT） 算法是一种对于图像的旋转、缩放和平移具有不变形性质的特征匹配算法，具有很高的稳健性[6]。

SIFT 算法首先通过对图像进行卷积运算构建图像尺度空间，生成像片金字塔；其次，剔除图像中的不稳定点；再次，记录特征点的方向并生成特征描述向量；最后，通过距离函数对特征点进行影像匹配。

2.4 TIN 的构建

首先，每张像片经过空中三角测量得到外方位元素真实值后，自动提取每张像片的特征点，生成点云数据，并对点云数据进行合并；其次，对点云数据构建不规则三角网（Triangulated Irregular Network，TIN） 模型，优化处理一些不合理的三角网；最后，生成TIN。

2.5 纹理映射

纹理映射技术是将纹理空间的纹理像素映射到屏幕空间的过程，即将地物纹理信息贴在三维模型上。对于无人机倾斜像片的纹理映射，国内外进行了许多研究。它的主要步骤为：首先，建立模型三角网与纹理三角网的对应关系；其次，建立像片纹理备选库；最后，选择合适像片进行映射并构建三维模型[7]。

2.6 基于Contextcapture Center 的集群技术

由于无人机采集的像片数据像幅小而导致采集像片数量多的问题，因此仅使用一台计算机处理会存在效率低的问题。

针对这一问题，英国奔特力系统软件公司开发出了Contextcapture Center 软件，在建立逻辑并行运算集群的基础上，使得多台电脑一起完成建模的任务[8]。

主机通过Contextcapture Center 软件将总任务进行人工划分，划分成多个子任务，并将子任务分配给多个副机，主机和副机一起完成任务，从而提高了数据处理效率。

2.7 三维模型质量评价

要对每个三维模型进行精度评价，就要对模型中的特征点平面和高程坐标进行评价。首先，通过全球导航卫星系统（Global Navigation Satellite System，GNSS） 与实时动态（Real-Time Kinematic，RTK） 载波相位差分技术获取每个特征点坐标（x测，y测，z测）；其次，在模型中量取检核点对应特征点坐标（x模，y模，z模）；最后，进行三维模型精度分析，其表达式方程组为

式中：Erms_xy为检核点的平面位置均方根误差；Erms_z为检核点的高程均方根误差；n为测区内检核点个数。根据CH/T 9015—2012 三维地理信息模型数据产品规范[9]中规定的三维产品模型的平面位置误差要求和高程误差要求（见表1） 对三维模型进行精度评价。

表1 平面位置误差要求和高程误差要求

3 消费级无人机模型构建精度评价的实验概况

3.1 实验测区概况

实验测区选择安徽理工大学山南校区（东经117.017 4°，北纬32.554 525°），主要以土地与环境学院及其附近区域为主，面积为0.03 km2，测区内包括教学楼、花坛、道路和斑马线等地物特征，可以较好地进行三维模型验证。

3.2 仪器参数

本次实验使用大疆“精灵”4 RTK 系列消费级无人机，搭载相机有效像素为2 000 万，相机焦距为8.8 mm，像元大小为2.4 μm，在飞行过程中具有自动避障功能。大疆“精灵”4 RTK 系列消费级无人机集成RTK 模块，定位精度可达水平10 mm、垂直20 mm。

测量像控点和检核点使用广州中海达卫星导航技术股份有限公司（简称“中海达”） 生产的i-RTK5 智能测量系统，搭载多星系统，i-RTK 平面定位精度为±（8+1×10-6D） mm，高程定位精度为±（15+1×10-6D） mm，其中D为被测点间距离。

航飞数据处理使用实验室高性能计算机进行处理，每台计算器均配置i7-8700 处理器和英伟达（NVIDIA） 公司生产的RTX1060 显卡，其内存为64 GB。

本实验使用6 台计算机搭载局域网组建集群，每台计算机上安装由英国奔特力系统软件公司开发的Contextcapture Center 软件进行模型构建。

3.3 数据采集

3.3.1 航飞数据采集

无人机采集像片时选择五向飞行，每一方案进行1 次正射飞行和4 次倾斜飞行，正射飞行时相机倾角为90°，倾斜飞行时相机倾角为60°。在飞行前，使用大疆开发的DJI GO 软件进行航飞规划，设置航向重叠率为80%，旁向重叠率为70%，依次设定80 m，100 m，120 m，140 m，160 m 的相对航飞高度飞行，不同相对航飞高度所对应的地面分辨率见表2。

表2 无人机的航飞数据采集相关参数

3.3.2 像控点布设和检核点采集

本次实验采用3 种像控点布设方案。图1 为像控点布设方案，其中圆点表示像控点。

1） 在测区4 个角点分别布设1 个平面高程点，共布设4 个像控点，见图1-a。

2） 在测区4 个角点分别布设1 个平面高程点，在2 条长边中点分别布设1 个平高点，共布设6 个像控点，见图1-b。

3） 在测区4 个角点分别布设1 个平面高程点，并在4 条边中点分别布设1 个平高点，共布设8 个像控点，见图1-c。

像控点标志使用红白相间长宽均为1 m 的标靶，见图2。

使用中海达i-RTK5 对像控点和检核点进行采集，采集像控点和检核点时，应查看手簿中接受卫星颗数、卫星高度角和位置精度衰减因子（Position Dilution of Precision，PDOP） 值，相关参数应遵循像控点观测要求，见表3。

应选择观测窗口状态为良好时进行采集，采集像控点时，每次采集30 个历元，采样间隔为1 min，同一个像控点应测量3 次，每次测量的像控点平面坐标不超过30 mm，高程坐标误差不超过50 mm。像控点坐标取3 次测量坐标的平均值。

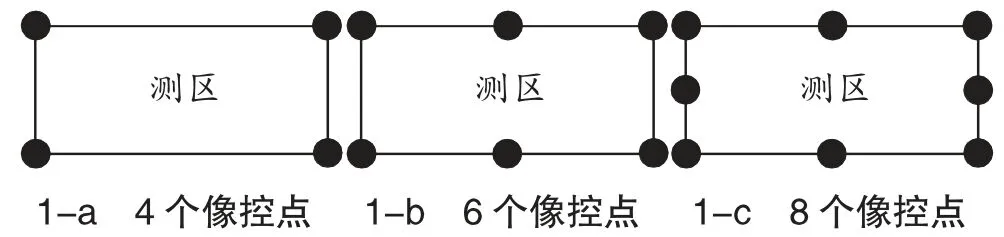
图1 像控点布设方案

图2 用于像控点标志的标靶

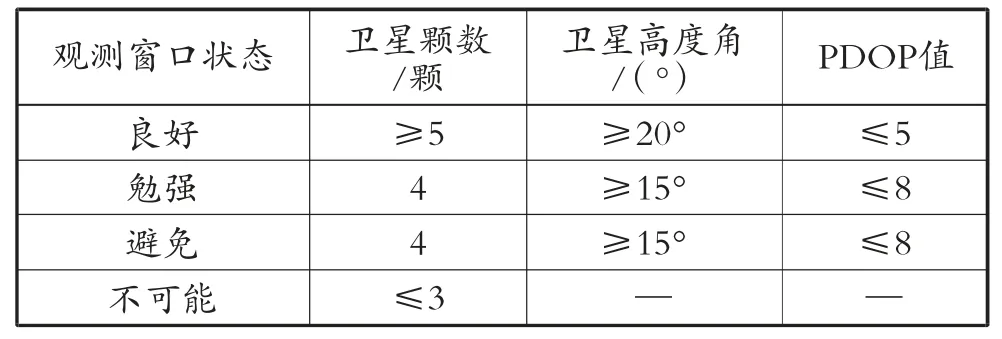
表3 像控点观测要求

由于实验测区位于学校内部，地物特征比较明显，因此在测区内选择斑马线端点、房屋角点等作为检核点，共选取21 个检核点。像控点和检核点坐标使用2000 国家大地坐标系（China Geodetic Coordinate System 2000，CGCS2000） 坐标，高程使用1985 国家高程基准。

3.3.3 三维模型特征点测量

在Contextcapture view 中打开构建的三维模型，通过模型的测量工具依次对21 个特征点进行测量，每个同名点测量3 次，同名点坐标取3 次平均值。

4 消费级无人机模型构建精度评价的实验分析

4.1 模型构建

本次实验设置了5 种不同相对航飞高度和3 种像控点布设方案，构建了15 个面积为0.03 km2的三维模型。

首先，通过对原始像片进行预处理和空中三角测量，导入像控点坐标；其次，生成三维密集点云，构造TIN 模型；最后，通过纹理映射等技术方法生成三维模型，见图3。

图3 当相对航飞高度为80 m 时的模型构建和展示

4.2 测区模型精度分析

首先，对不同相对航飞高度和不同像控点布设方案下的三维模型进行精度分析；其次，通过Contextcapture Center 软件中的模型测量工具，测量出检核点的模型坐标；最后，计算各个模型的均方根误差。

不同相对航飞高度所构建三维模型的平面位置均方根误差和高程均方根误差见图4。

1） 当相对航飞高度一定时，不同像控点布设方案的三维模型平面位置均方根误差和高程均方根误差不相同。

当相对航飞高度为80 m 时，当像控点布设数量为4 个、6 个、8 个时，对应的三维模型平面位置均方根误差分别为54 mm，50 mm，44 mm；对应的三维模型高程均方根误差分别为73 mm，56 mm，46 mm。

当相对航飞高度为160 m 时，当像控点布设数量为4 个、6 个、8 个时，对应的三维模型平面位置均方根误差分别为102 mm，97 mm，84 mm；同时对应的三维模型高程均方根误差分别为129 mm，112 mm，96 mm。

由图4 可知，当相对航飞高度一定时，随着像控点布设数量的增加，三维模型的平面位置均方根误差和高程均方根误差逐渐减小，精度逐渐升高。

2） 当像控点布设数量相同时，不同相对航飞高度所构建三维模型的平面位置均方根误差和高程均方根误差存在差异。

当像控点布设数量为4 个时，相对航飞高度分别为100 m，120 m，140 m 时构建的三维模型平面位置均方根误差为64 mm，74 mm，89 mm；高程均方根误差为84 mm，105 mm，114 mm。

图4 三维模型误差

由图4 可知，当像控点布设数量一定时，三维模型的精度随着相对航飞高度的升高而降低。

3） 构造的15 个测区三维模型中，平面位置的最高精度为44 mm，高程的最高精度为46 mm；平面位置的最低精度为102 mm，高程的最低精度为129 mm，均符合CH/T 9015—2012 三维地理信息模型数据产品规范[9]中规定的I 级要求。

5 结论

本文以安徽理工大学地球与环境学院周边面积为0.03 km2的地区为实验测区，通过外业数据采集并运用集群技术对内业数据进行处理，构造出15 个三维模型，通过不同像控点布设方案和不同相对航飞高度验证消费级无人机的建模精度，分析实验结果并得出如下结论。

1） 当像控点布设方案不变时，相对航飞高度越高，建模精度越低；当相对航飞高度一定时，像控点布设数量由4 个增加到8 个时，像控点数量越多，模型精度越高。

2） 在构建的15 个三维模型中，平面位置的最高精度可达44 mm，高程的最高精度可达46 mm，可以达到厘米级测量需求。

综上所述，消费级无人机建模精度能够达到厘米级，具有重要的工程实用价值。本文仅考虑相对航飞高度和像控点布设数量对消费级无人机建模精度的影响，下一步将会从像片重叠率、像控点排列方式等方面研究对消费级无人机建模精度的影响。