低压电器企业综合竞争力的动态因子分析
代迎波 孙琪荣 刘雯 李雪 王剑嵘 戴伟倩 聂军
中国电器工业协会通用低压电器分会(挂靠单位:上海电器科学研究院)
关键字:低压电器;动态因子分析;综合竞争力
0 引言
低压电器行业统计的实际工作中,为了全面系统地、动态地反映企业情况,往往逐年连续、收集较多变量,但因所收集的变量间存在较强相关关系,实际的评价往往是选取若干科学、 有效的指标,希望通过采用较少的新指标代替原来较多的原变量,这些新指标尽可能地反映原变量的信息,可对其进行采用因子分析,但如果要对行业在某一连续时间段的动态情况做出科学性的评价比较和排序分析,就需引入一个时间维度,通过动态因子分析对指标纵向变化进行对比分析,充分体现了动态性,使得分析更加透彻,差距结果更加明显。
1 因子分析模型
因子分析将具有错综复杂关系的变量(或样品)综合为数量较少的几个因子,以再现原始变量与因子之间的相互关系,探讨多个能够直接测量,并且具有一定相关性的实测指标是如何受少数几个内在的独立因子所支配的,同时根据不同因子还可以对变量进行分类,属于多元分析中降维的一种统计方法。
因子分析是通过研究多个变量间相关系数矩阵(或协方差矩阵)的内部依赖关系,找出能综合所有变量的少数几个随机变量,这几个随机变量是不可测量的,通常称为因子。然后根据相关性的大小把变量分组,使得同组内的变量之间相关性较高,但不同组的变量相关性较低。
各个因子间互不相关,所有变量都可以表示成公因子的线性组合。因子分析的目的就是减少变量的数目,用少数因子代替所有变量去分析整个经济问题。因子模型如下:
设有N个样本,P个指标,X=(X1,X2,…,XP)T为随机向量,要寻找的公因子为F=(F1,F2,…,Fm)T,则模型
矩阵A=(aij)称为因子载荷矩阵,引为因子载荷(Loading),其实质就是公因子Fi和Xj变量的相关系数。ε为特殊因子,代表公因子以外的影响因素,实际分析时忽略不计。
对求得的公因子,需要观察它们在哪些变量上有较大的载荷,再据此说明该公因子的实际含义。如果难于对因子Fi给出一个合理的解释,需要进一步作因子旋转,以求旋转后能得到更加合理的解释。
得到初始因子模型后,因子载荷矩阵往往比较复杂,不利于因子的解释。因子可以通过因子轴的旋转,使得载荷矩阵中各元素数值向0~1分化,同时保持同一行中各元素平方和(公因子方差)不变。通过因子旋转,各变量在因子上载荷更加明显,因此也有利于对各公因子给出更加明显合理的解释。
求出公因子后,还可以用回归估计等方法求出因子得分的数学模型,将各公因子表示成变量的线性形式,并进一步计算出因子得分,对各案例进行综合评价。
动态因子分析的思路是要引进时间。可以对要考察的n年指标矩阵,分别乘上相应的时间权重ω(ti),i= 1 , 2,…,n,得到一个时间加权矩阵,然后利用此矩阵数据进行因子分析。时间权重的确定有主观赋权法和客观赋权法。主观赋权法,可根据实际出发,选择适合的时间权重系数,方便进行分析。
2 2017~2019年低压电器行业企业综合实力
本文使用因子分析综合评价方法,对115家低压电器行业企业连续上报的经济报表中的2017~2019年的企业基本情况和财务情况表的面板数据进行分析,并综合实力评价各企业的地位和发展状况。在分析过程中,本文选取了年报中能足够反映经济发展总体水平的32项主要指标。我们首先用 SPSS统计软件将 2017、2018、2019年原始矩阵标准化,并根据距现在越近对于我们分析越有价值的实际情况,对2017、2018、2019年的时间权重主观赋值为16%、34%、50%,得出时间加权矩阵。分析的过程中,采用主成分法,将特征值大于1的主成分看作公因子,得到的方差最大的正交旋转后的特征值、贡献率,因子载荷矩阵、累计贡献率表如表1所示。

表1 KMO and Bartlett’s Test
为保证数据模型的结构效度,能够实施因子分析的必要条件是KMO的检验值大于0.5并且巴特利特球型度检验显著性P值小于0.05。由KMO统计量0.912可以看出并且Bartlett检验,Sig值为0.000小于显著水平0.05,可以看出非常适合做因子分析。
由相关系数矩阵R计算得到特征值、方差贡献率和累积贡献率,由表2可知,前4个特征根大于1,因此SPSS只提取了前4个公因子,前4个因子的方差贡献率仍为87.989% ,因此选前4个因子己足够描述2017~2019年低压电器企业的情况。
因子分析要求提取出的公因子有实际含义,为了使因子载荷矩阵中系数更加显著,可以对初始因子载荷矩阵进行旋转,使因子和原始变量间的关系进行重新分配,相关系数向0~1分化,旋转前后各变量散点的相对位置保持不变,即旋转并不改变因子分析的整体结果,只是影响各因子在各变量上的载荷分布,并影响各因子的贡献率。从而更加容易进行解释,本文采用方差最大正交旋转后的矩阵如表3如示。
可以看出:
1)第一公因子在主营业务成本、主营业务收入、全年工业总产值当年价、全年工业销售产值当年价、出口交货值、工业增加值、低压元器件收入、低压元器件产值等有较大的载荷,可以命名为盈利能力;
2)第二公因子在年末资产合计、年末所有者权益合计、流动资产小计、年末研究与试验发展人员、年末负债合计等有较大的载荷,可以命名为资本结构运作能力;
3)第三公因子在全年从业人员平均人数、自年初累计完成固定资产投资等有较大的载荷,可以命名为人员要素投入运作能力;
4)第四公因子在固定资产净值年平均余额、其他业务收入、固定资产小计等有较大的载荷,可以命名为长期资产价值能力。

表2 总方差解释
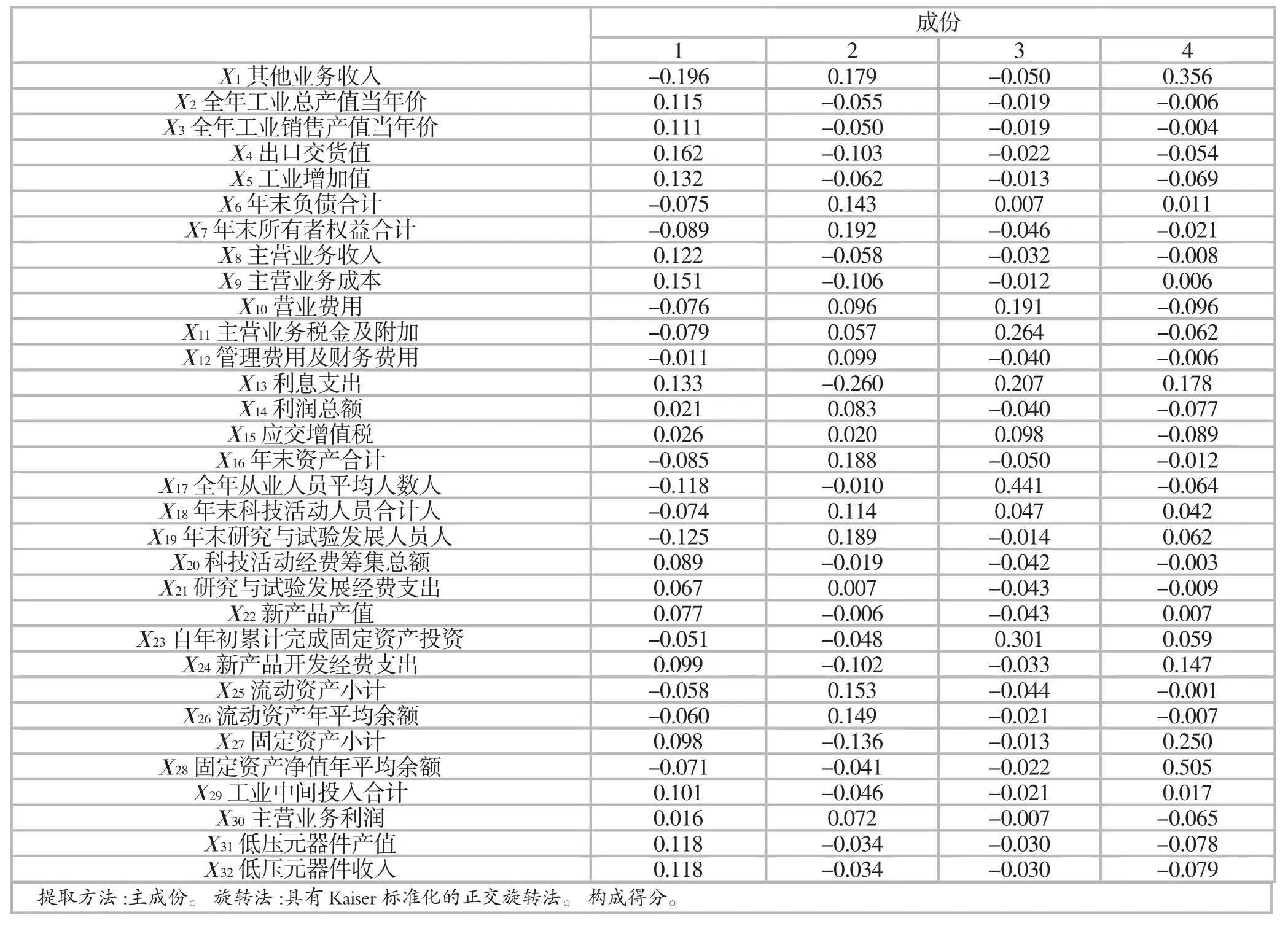
表3 旋转后的成份矩阵
这四个因子的性质及其顺序较好地体现了其代表的能力/资源对企业的实力的影响,也完全符合行业近几年的企业的发展的推力因素。
(3)2017~2019年低压电器企业的综合能力评价
为了考察各企业的发展状况,并对其进行分析和综合评价,采用回归方法求出因子得分函数,SPSS输出的函数系数矩阵如表4所示。
由系数矩阵将四个公因子表示为32个指标的线性形式。4个公因子得分函数为:
F1=0.115×全年工业总产值当年价计-0.196×其他业务收入+…
F2=-0.055×全年工业总产值当年价+0.179×其他业务收入+…
F3=-0.019×全年工业总产值当年价-0.050×其他业务收入+…
F4=-0.006×全年工业总产值当年价+0.356×其他业务收入+…
四个公因子分别从不同方面反映了行业企业的经济发展状况的总体水平,但单独使用某一公因子并不能对各企业的地位作出综合评价,因此,经过对4个公因子进行加权求和,权数取其方差贡献值或方差贡献率,本文中采用方差贡献率作为权重,4个旋转后的公因子的方差贡献率依次为39.240%、30.392%、10.582%、7.776%,于是可得个企业的综合得分(ZF)的计算公式如下:
ZF=39.240%×FAC1_1+30.392%×FAC2_1+10.582%×F AC3_1+7.776%×FAC4_1。其中,F1、F2、F3、F4的计算公式分别如下:F1=39.240%×FAC1_1、F2=30.392%×FAC2_1、F3=10.582%×FAC3_1、F4=7.776%×FAC4_1。
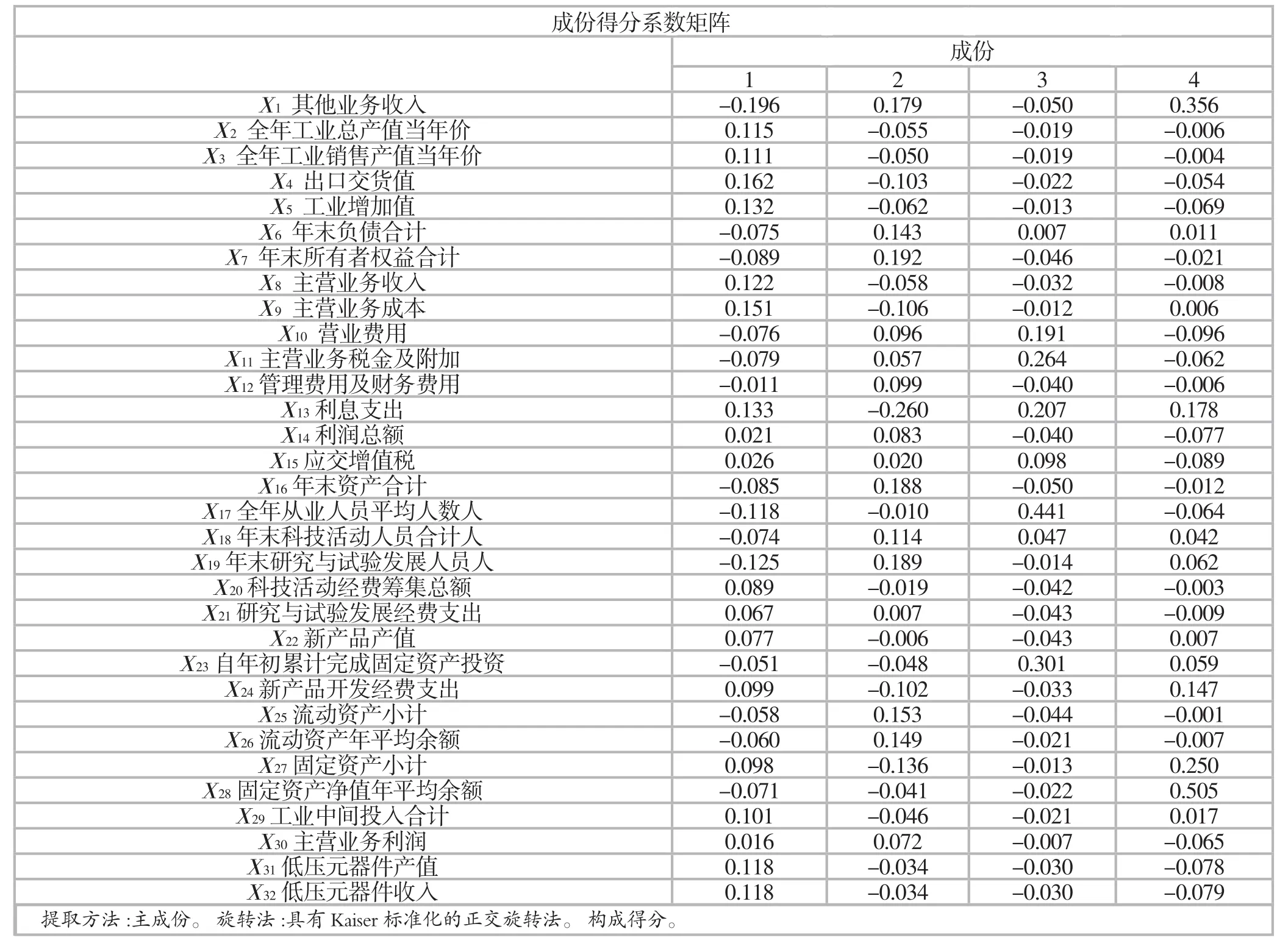
表4 成份得分系数矩阵
得到综合因子得分表 ,并求出各企业2017~2019年的各因子得分的排序,如表5所示,
到综合因子得分表 ,并求出各企业2017~2019年的各因子得分的排序,如表6所示。
在最终得到的综合得分里,显示了各企业、各年度动态变化情况。从表中结果可知:
第一公因子:盈利能力,可以看出,2017~2019年该因子得分数表现靠前的企业有:公司A、公司B、公司C、公司G、公司D、公司E、公司F、公司H、公司I、公司J、公司L、公司O等。
第二公因子:资本结构运作能力,可以看出,2017~2019年该因子得分数表现靠前的企业有:公司A、公司D、公司E、公司H、公司G、公司S、公司J、公司F等,与这些企业的资本运作、股权激励等事实一致。
第三公因子:人员要素投入运作能力,可以看出,2017~2019年该因子得分数表现靠前的企业有:公司F、公司C、公司E、公司G、公司B等。
第四公因子:长期资产价值能力,可以看出,2017~2019年该因子得分数表现靠前的企业有:公司F、公司H、公司K、公司L、公司A、公司I、公司S等、
ZF综合因子得分表现靠前的企业有:公司A、公司B、公司C、公司D、公司E、公司F、公司G、公司H等。
3 结束语
本文实证结果得知,低压电器企业综合实力受多个指标
影响,且每个指标的作用大小不尽相同,通过各种因子动态作用或助力个企业的实力的逐步形成,上述分析表明:

表5 2017~2019年行业企业各因子及综合因子动态变化情况

表6 2017~2019年行业企业各因子及综合因子动态变化情况
1)综合实力与公司规模大小基本一致,这说明企业综合规模对企业综合实力影响重大,这些结论都与实际相符。
2)动态因子的研究表明,行业企业的资本结构、人员要素投入运作、长期资产价值正在逐步形成,逐渐形成该企业的独特优势。
3)低压电器企业的综合实力构建是一项复杂的、动态过程。不仅受到企业自身投入的各种因素影响,更重要的是企业对所有要素的运营和打造的能力的过程,同时,也与整个社会经济环境、投资环境及国家政策息息相关。因此,今后还可以从国家政策、经济环境和产业布局等方面来全面考察行业的综合发展。

