基于EDEM 的洛稻籽粒堆积仿真研究

孔令今杨开敏王梦月

(山东建筑大学 热能工程学院，山东 济南250101)

0 引言

在粮食储藏过程中，稻谷等粮食籽粒的堆积进料是首要问题。 深入研究并掌握粮食籽粒堆积形成粮堆的机制，是简化籽粒模型构建过程和缩短籽粒堆积仿真模拟时间的重要措施。 在使用软件模拟粮食籽粒的堆积过程时，首要解决的是如何进行非球形粮食籽粒的填充，但是在构建非球形籽粒模型时，大多采用自动填充模式进行非球形籽粒的填充。 王美美等[1]对玉米籽粒进行自动填充，填充的过程需要引入二次开发系统，填充非球形籽粒所需的球形籽粒数量为351 个；原建博等[2]通过非接触式三维激光扫描法重构水稻籽粒，自动填充籽粒模型的填充球数为203 个，填充过程耗时为1 h；刘彩玲等[3]通过三维激光扫描等技术重构水稻籽粒，填充颗粒模型的球数为87 个。 但是，在实际的计算过程中，上述方法由于EDEM 的仿真模拟计算需要考虑到每一个球体之间的接触力和每一个球体与壁面的接触力，导致用数量多的球形籽粒填充非球形籽粒模型时计算的过程非常复杂，大幅增加了计算时间。

在仿真模拟过程中，多采用对比实验与堆积角测量以验证籽粒仿真模型各项参数的准确性。 目前，实验法测籽粒物料堆堆积角的主要方法有排除法[4-5]、注入法[6-8]和倾斜法[9]。 在大型粮食储备仓库中，进料时一般采用皮带传送，将粮食籽粒以抛物线形式送入粮仓，粮食籽粒在粮仓内的堆积过程为自由落体式下落过程，而注入法最符合实际的籽粒堆积过程，因此模拟实验中常采用注入法，使洛稻通过漏斗自上部流入，在底部形成圆锥状堆积角。

文章选取洛稻998 籽粒测量其长、宽、厚、球度等尺寸参数，统计出粮食籽粒粒径的分布规律等；利用软件EDEM 基于离散元法实现粮食籽粒堆积的仿真模拟，对非球形籽粒进行手动填充，同时实验采用注入法测得籽粒物料堆的堆积角，将结果进行对比分析，验证软件EDEM 以手动填充方式进行非球形洛稻籽粒填充的可行性，以期能够减少籽粒模型构建单体的数量，简化籽粒构建过程和缩短仿真模拟时间，为以后测量籽粒堆积体的孔隙率和探究料堆的传热传质等提供尺寸参数和籽粒模型，可以更好地指导实际的工程。

1 基于离散元法的籽粒模型建立

1.1 籽粒的理论接触模型

对球形籽粒建立接触模型，如图1 所示。

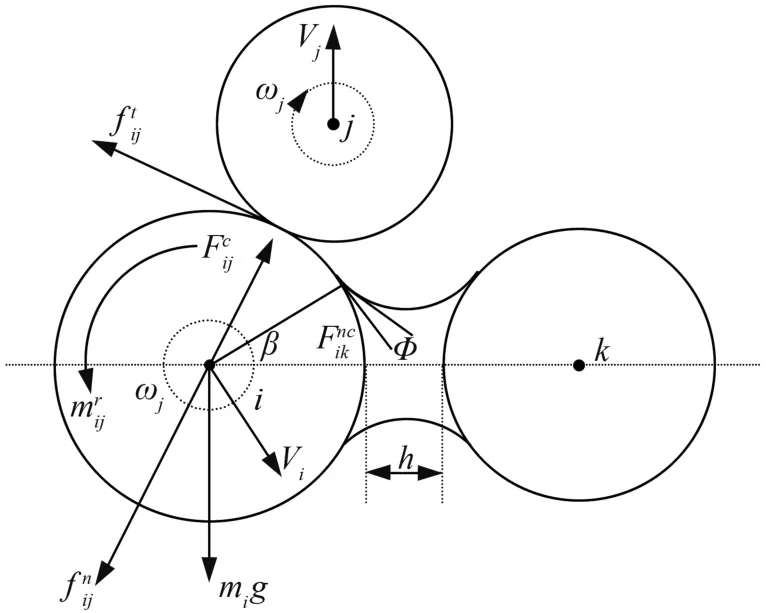
图1 球形籽粒接触模型图

籽粒i在任意时刻t的控制方程[10]由式(1)和(2)表示为

式中:mi为籽粒i的质量，kg；Ii为转动惯量，kg·m2；vi为速度，m/s；wi为角速度，rad/s；ki为与籽粒i发生接触的颗粒的数量；Tij为扭矩，N·m；mig为籽粒i的重力，N；fcontact，ij为接触力，N；fdamp，ij为阻力，N。

1.2 离散元法的接触模型方程

离散元法DEM(Discrete Element Method) 是Cundull 和Strack 于1971 年提出的一种模拟籽粒材料静态与动态行为的研究方法[10]。 离散元法将求解空间离散为离散单元阵，各个单元之间是不连续、可分离的，即一个单元可以与其相邻的单元接触或分开[11]，可将分析对象看成充分多的离散介质，每个籽粒或块体为1 个单元。 DEM 的基本思路是利用籽粒接触模型计算相互接触单元间的受力，并利用牛顿第二运动定律求解籽粒的运动参量[12]，即全过程中的每一时刻各籽粒间的相互作用，接触力和每个离散单元的运动状态。

引入时间步长的概念，递归地求解离散单元的运动过程，交替反复运算，实现籽粒运动情况的预测[2]。 对于非球形籽粒的接触模型可选用软球模型，其将籽粒间的法向力简化为弹簧、阻尼器和滑动器，引入弹性系数和阻尼系数参量，不考虑籽粒表面变形，依据籽粒间发现重叠和切向位移计算接触力[3]。

接触模型方程[13]如下:

将籽粒接触过程中的振动运动进行法向和切向分解，法向振动运动方程式Fn由式(3)表示为

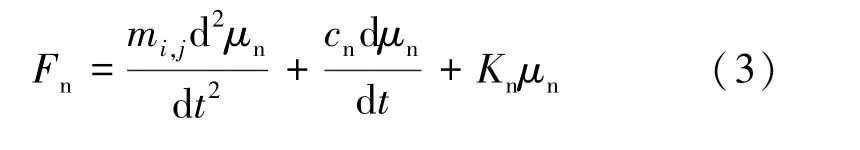
籽粒接触过程的切向振动运动表现为切向滑动与籽粒的滚动，其切向分量Fs方程式、籽粒所受的外力矩M分别由式(4)和(5)表示为

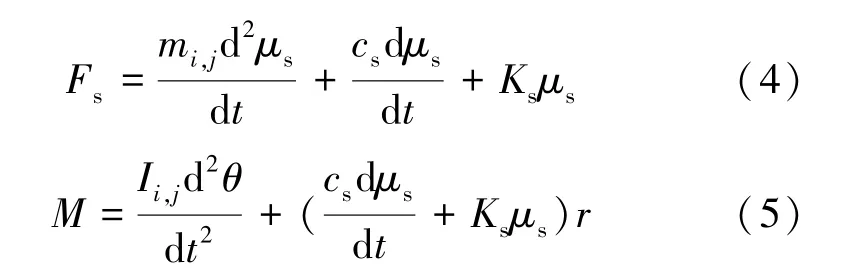
式中:mi，j为籽粒i、j的等效质量，kg；Ii，j为籽粒i、j的等效转动惯量，kg·m2；r为旋转半径，m；μn、μs分别为籽粒的法向和切向相对位移，m；θ为籽粒自身的旋转角度，rad；Kn、Ks分别为接触模型中的法向及切向弹性系数；cn、cs分别为接触模型中的法向及切向阻尼系数。

2 洛稻998 籽粒堆积的实验测定

2.1 实验测量仪器

实验仪器包括500 g 托盘电子秤(精度为0.01 g)、0～150 mm 电子游标卡尺(精度为0.02 mm)、量角器(精度为0.01°)、不锈钢漏斗(底径为15 mm)、不锈钢托盘(200 mm×200 mm)。

2.2 洛稻998 籽粒尺寸参数的测量

实验随机选取100 粒洛稻998 籽粒，重约3.06 g，利用游标卡尺对籽粒的长度L、宽度W、厚度T进行测量[14]，计算出球度，如图2 所示。 为避免随机误差，可测量100 次籽粒尺寸，求得平均值和标准差，获得数据见表1。

图2 籽粒尺寸参数测量图

表1 洛稻998 尺寸参数测定表/mm

对长度、宽度和厚度所测数据进行数据统计，并依据测量数据绘制洛稻998 籽粒的几何尺寸分布曲线，如图3 所示。 洛稻998 籽粒长度、宽度、厚度尺寸分别集中分布在7.2～7.4、3.3～3.4 和2.3～2.5 mm之间，尺寸参数的标准差较小，数据集中性较强，尺寸参数的比例分布符合正态分布规律。

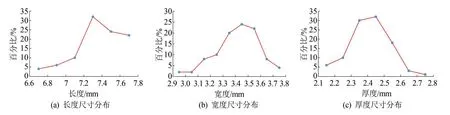
图3 洛稻998 种子几何尺寸分布图

王磊[15]在对类球形蔬菜种子进行了研究，得出了球度SP的计算方程由式(6)表示为

将所求的洛稻998 籽粒尺寸参数带入式(6)，计算得到球度为53.24%，因此在EDEM 中建立模型时将籽粒视为椭球型。

张桂花等[7]在对包衣稻种物理特性的研究中，将稻种的3 轴尺寸测得后以3 轴平均值作为单一粒径。 将洛稻998 籽粒的尺寸参数进行计算，得到单一粒径为4.40 mm。

综上所述，实验测得的洛稻998 籽粒尺寸可以作为下一步EDEM 仿真的数据依据。

2.3 洛稻998 籽粒料堆的堆积角测定

实验中参考田晓光等[6]做法，制作固定底面的不锈钢漏斗装置，漏斗底直径为15 mm，约为颗粒单一粒径的3 倍以上，防止在堆积过程中发生堵塞等对实验结果产生影响。 设置不锈钢漏斗的底端和不锈钢托盘的距离为100 mm，尽量真实地模拟粮食籽粒在粮仓堆积过程中的自由下落过程，以保证测得的堆积角数据可靠。

李海伟[16]根据JB/T 9014.7—1999《连续输送设备散状物料堆积角的测定》[17]对散状物料的堆积角进行了测定，堆积角定义为当散状物料自由堆积在水平面上，且保持堆形面与水平面的最大夹角。 籽粒在粮仓实际进料过程中，底部保持静止，粮食籽粒自由下落，静态堆积角θi测量方程由式(7)表示为

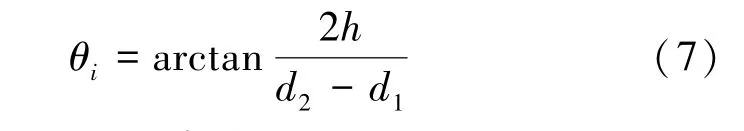
式中:h为料堆的测量高度，mm；d1为料堆测量上底底径，mm；d2为料堆的测量底径，mm。

随机选取洛稻998籽粒共计2000粒，重约为61.27 g。 将籽粒倾倒入不锈钢漏斗中，使籽粒在重力的作用下运动，最终形成的料堆静态堆积角如图4 所示。

图4 料堆静态堆积角图

重复实验10 次，计算料堆的测量高度和料堆的测量底径并取平均值，得到的统计数据见表2。

表2 料堆测量的高度和底径表/mm

测量料堆的平均高度h、上底底径d1、底径d2分别为4.05、3.98 和13.93 mm，将值代入到式(7)可得实验测得的堆积角为39.15°。

3 基于EDEM 的籽粒堆积仿真

3.1 非球形籽粒单体建模

基于上述实验所测得的尺寸参数可知，洛稻998 的外形可视为椭球型。 在EDEM 中用球形籽粒进行手动填充，分别选取7、11、16 个球形籽粒的3种工况，进行洛稻998 的非球形籽粒单体的填充，便于在测试堆积角过程中进行对比试验，填充模型如图5 所示。

由图5 可知，非球形籽粒填充单体模型的外形接近于洛稻998 籽粒，在模拟过程中的单一颗粒质量为0.03 g，实际籽粒的质量约为0.030635 g，在密度参数设定相同的情况下，非球形籽粒模型的体积与实际籽粒体积大致相同。

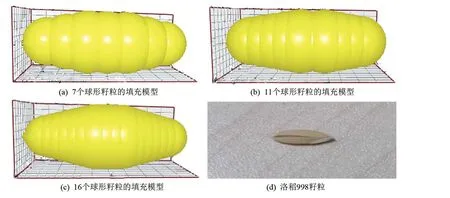
图5 非球形籽粒填充模型图

3.2 非球形籽粒堆积模型建立

在实际粮食籽粒的堆积过程中，粮食籽粒之间会存在静摩擦力和滑动摩擦力，籽粒与壁面之间也同样存在这两种摩擦力；籽粒与籽粒之间或者籽粒与壁面之间发生碰撞，会发生形变。 实验测定中的籽粒—籽粒和籽粒—壁面之间的滚动摩擦力在EDEM 仿真模拟时以滚动摩擦系数的设置体现；当籽粒从漏斗底部直径为15 mm 的漏口自由落下时，其与不锈钢托盘之间的滚动摩擦力和弹性模量会对籽粒堆积角的角度产生影响，在EDEM 仿真过程中同样要设置弹性模量等参数，才能够更加准确地模拟实际粮食籽粒在进料过程中的堆积现象，使仿真模拟的结果符合工程实际。

在EDEM 软件仿真构建时，设置漏斗材质为不锈钢材质，内部构建虚拟的静态籽粒工厂，颗粒总数设为2000 粒，底部托盘材质为不锈钢材质。 洛稻998-洛稻998、洛稻998-不锈钢的恢复系数、静摩擦系数和滚动摩擦系数等设置[18-22]见表3。

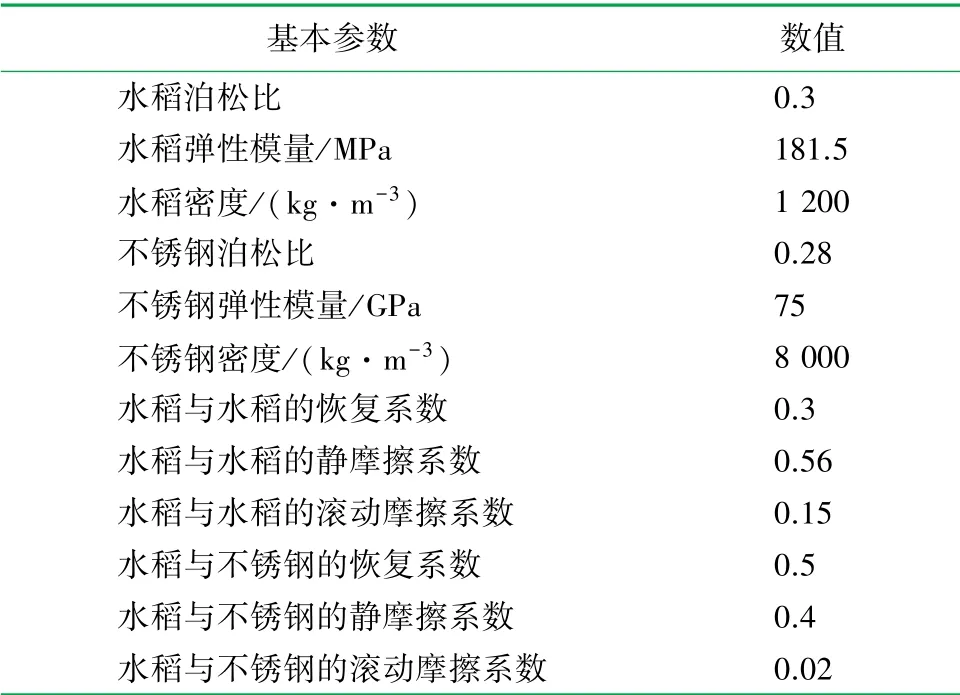
表3 基于EDEM 的籽粒堆积仿真模型所需参数表

对于洛稻998 的籽粒物理模型方程，选用软件中的Hertz-Mindlin(no slip)模型作为颗粒接触模型，建立籽粒堆积模型如图6 所示。 籽粒物堆积角仿真模拟实验采用Euler 模型，时间步长设为Rayleigh 时间步长的30%，计算单元格设为最小单元格的3 倍，总的仿真模拟时间设为6 s，其中重力加速度为9.81 m/s2，数据保存时间设为每0.01 s 保存一次，待仿真模拟过程完成后，进行堆积角的测量。

图6 籽粒堆积模型图

3.3 仿真模型堆积角的测量与分析

由7、11 和16 个球形籽粒构建的单体洛稻998进行堆积模型仿真模拟，如图7 所示，仿真模拟堆积完成的时间分别为2.68、2.84、2.96 s，实际的堆积时间分别为0.57、1.6 和2.7 h。

根据实验数据可知，在最大限度不改变非球形籽粒外形尺寸的前提条件下，随着堆积所需球形籽粒个数的减少，堆积所需的时间约可缩短为采用自动填充法用多个球形颗粒单体填充籽粒模型进行堆积所需时间的70%。

粮堆处于静态，将EDEM 后处理中的剪切(Clipping)和工具(Tools)中的量角器(Protractor)相结合测量堆积角的角度，以XOZ 面为基准建立切面，利用量角器进行角度的测量，如图8 所示，不断改变x轴和z轴的数值，使测得的角度更加接近实际值。 测量10 次后取平均值，测得的堆积角数据统计结果见表4。

图7 3 种单体籽粒堆积图

由表4 可知，由7、11、16 个球形籽粒构建的单体洛稻模型在相同的参数条件下堆积完成后测得的堆积角分别为42.82°、42.08°、41.88°，3 种工况测得的仿真堆积角数值上差别很小，与实验注入法测得的堆积角39.15°对比，偏差分别为9.37%、7.48%、6.97%，数据之间的偏差均＜10%，从而在EDEM 中验证了手动填充非球形籽粒具有可行性。

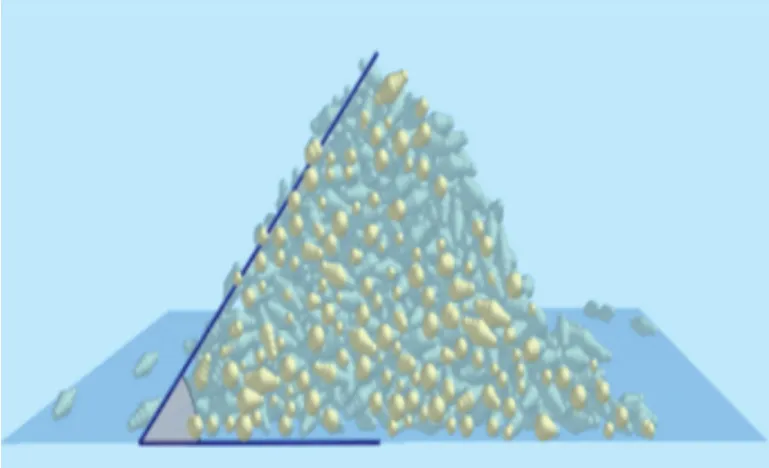
图8 堆积角测量图

表4 3 种单体模型堆积建模测得的堆积角统计表/(°)

4 结论

根据上述研究结果，可得出主要结论如下:

(1) 大量实测数据得到了洛稻籽粒平均尺寸参数，通过绘制长度、宽度、厚度的比例分布曲线，验证其符合正态分布，并基于此参数进行EDEM 非球形籽粒手动填充，填充的非球形籽粒模型体积与实际籽粒体积相近，进而验证了所测得的籽粒尺寸参数正确性。

(2) 球形籽粒构建的3 种单体洛稻998 模型进行堆积仿真模拟形成的静态堆积角与实验注入法测得的堆积角相比较，计算数据偏差＜10%，说明实际粮食籽粒的下落堆积过程可以通过EDEM 仿真模拟实现，验证了手动填充非球形籽粒具有可行性。

(3) 在保证非球形籽粒尺寸参数和接触参数等参数与实际测量值相同的情况下，EDEM 用较少的球形籽粒填充出来的非球形籽粒可以模拟实际的粮食进料过程，能够简化非球形籽粒的填充过程，堆积所需的时间约可缩短为采用自动填充法所需时间的70%。