运动单轴各向异性介质的电磁波传输特性
华雪侠
(咸阳师范学院 物理与电子工程学院,陕西 咸阳 712000)
对于电磁波在介质中的传播,很多专家学者都进行了研究和讨论,给出了静止各向异性介质的描述[1-4]。一些研究根据Lorentz变换,系统讨论了运动各向同性均匀介质的电磁波传播特征[5-7]。另外一些文献给出了单轴各向异性介质的状态方程的相关变换式[8-9]。但大多数文献都只对静止状态下的各向异性介质进行探讨,对电磁波在运动各向异性介质中传输的讨论较少。事实上介质往往是各向异性且运动的,因此分析电磁波在运动各向异性介质中的传播特性是很有必要的。本文在上述文献整理工作基础上,利用Lorentz变换矩阵,详细推导了运动坐标系下的单轴各向异性介质的本构关系,并讨论了电磁波在其中的传输特征。
1 运动单轴各向异性介质的本构方程
1.1 单轴各向异性介质描述
各向异性介质的本构关系可简写为

(1)
考虑单轴各向异性介质,则在直角坐标系中,介电常数和磁导率为对角张量,则媒质参数为
(2)
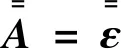
1.2 运动单轴各向异性介质的本构关系
s系中静止介质的状态方程为
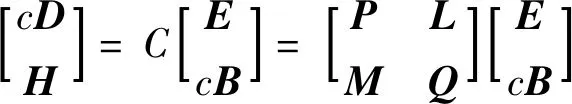
(3)
则相对s′系静止的介质的状态方程为

(4)
利用洛伦兹变换,s系中电磁场变换到s′系中为
(5)


(6)
根据上述公式,可解得运动各向异性介质本构关系:
(7)
式中:

(8)
当两坐标系相对静止时,则ν=0,β=0,式(8)则变为各向同性介质,即ε′=ε,μ′=μ。
2 波在运动单轴介质中的传播特征
2.1 运动单轴各向异性介质本构关系的DB表示
由状态方程(5)~方程(7)解得
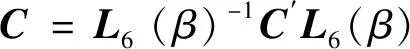
(9)
设s′系相对于s系以v速度沿z轴运动时,则对于运动单轴各向异性介质有
(10)
则单轴各向异性介质的本构关系的DB表示为
(11)
其中的本构参数为
(12)
由式(2)可知,速度v沿z轴方向,则矩阵元素取决于速度,并且在静止状态下,运动介质为单轴介质的时候,本构关系还是取于上式相应的状态方程。
2.2 单轴各向异性介质的波
在各向异性介质中,以D,B表示E,H,即
(13)
用方程形式表示为
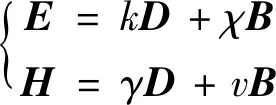
(14)
对于静止单轴介质:
(15)
对于运动单轴介质:
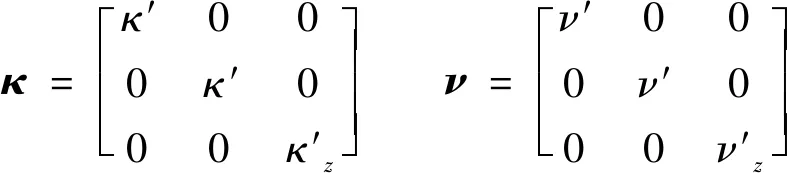
(16)
将运动单轴介质的本构关系CDB转到KDB系统中,则对应的状态方程的本构参数变为

(17)
将式(17)代入式(16)中,则可以得到以下方程:
(18)
由直角坐标系系与KDB系的转换关系可得:
(19)
由此得到传播参数:
Ⅰ型波:
(20)
(21)
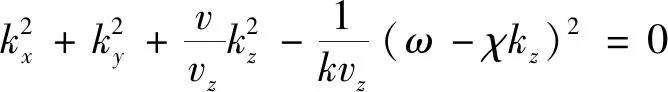
(22)
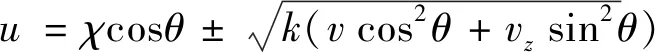
(23)
Ⅱ型波:
(24)
(25)

(26)
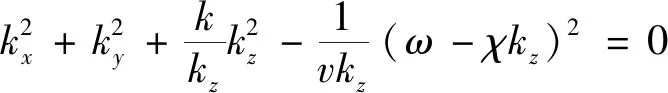
(27)
式中:±号表示方向,“+”表示与介质传播的方向相同,“-”表示则与介质的传播方向相反。
即对运动单轴介质V=zv时,有

(28)

(29)
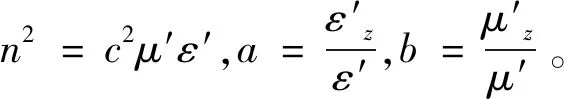
3 结论与分析
在洛仑兹变换的基础上,利用介质的状态方程,各向异性介质的性质,以及KDB系统的转换关系,详细地推导了运动单轴各向异性介质的本构方程以及传播中的参数。下面依据介质运动方向分为三种情况讨论:
(1)若介质速度在x轴方向传播,则kz=0,k矢量为
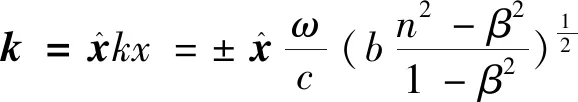
(30)

(31)
式中:±号表示介质沿x轴正方向和负方向传播。当β从0增到1时,k从anω/c或者bnω/c增加到无穷大。从而,当介质速度接近于真空中的光速时,沿z轴方向速度为0。
(2)若介质速度在y轴方向传播,则kz=0,k矢量为
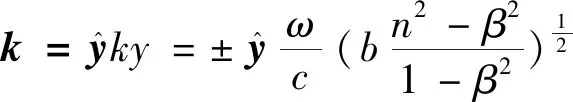
(32)

(33)
当β从0增到1时,k从anω/c或者bnω/c增加到无穷大。从而,当介质速度接近于真空中的光速时,沿z轴方向速度为0。
(3)若介质沿z轴传播,则kx=ky=0,这时候两种波转换为一种波,k则变成为
(34)
式中:对应的介质沿z轴正方向传播。当β从0增到1时,k从nω/c减为ω/c,对应的波速从c/n增到c。
(35)
式中:对应的介质沿z轴负方向传播。当β从0增到1/n时,k从-nω/c减为-∞,对应的波速从-c/n增到0。

