一种新型电磁真空泵的优化设计
柯燕峰,常思勤,谭 草
(南京理工大学机械工程学院,江苏 南京 210094)
1 引言
传统膜片式真空泵因具有密封性高,耐久性好,振动小,噪声低等优点而得到广泛应用。但其存在质量大、成本高等问题,因此提出了新型电磁膜片式真空泵,其利用新型双作用脉冲电磁铁直驱,具有工作频率可实时快速调节,质量体积相对小,成本、功耗低等优点[1],且无需中间转换机构,直接驱动膜片做往复变形运动,工作效率高[2]。
单向阀作为真空泵气体通断的关键部件,对泵的性能影响很大。目前,真空泵的单向阀大多以球阀、锥形阀等传统单向阀为主,但阀芯质量较重,响应速度慢,限制了真空泵的性能提升[3],因此采用簧片阀作为电磁真空泵的单向阀。
文献[4-6]采用理论计算与实验相结合的方法对真空泵性能进行研究,研究方法耗时较长,经济性差。文献[7]利用Matlab/Simulink建立了往复式压缩机工作过程的仿真模型,并利用实验验证了模型准确性。文献[8-9]通过优化旋片式真空泵的多个结构参数实现了性能的有效优化。因此鉴于上述研究,建立了电磁真空泵工作过程的Matlab/Simulink仿真模型,并通过实验验证了模型准确性。在此基础上,以抽气性能为优化目标,通过建立簧片阀刚度及等效质量与结构参数间的关系式,进行了簧片阀组的协同优化,从而有效提升了电磁真空泵的抽气性能。
2 结构与原理
电磁真空泵为往复膜片泵结构,两级串联工作,可有效提高极限真空度,它主要由作为驱动部件的双作用脉冲电磁铁(其运动部件为动铁)以及泵体、进口管、出口管、簧片阀、连接杆、膜片等部件组成。其结构和工作原理示意图,如图1所示。

图1 电磁真空泵结构示意图Fig.1 Schematic Diagram of Electromagnetic Vacuum Pump
簧片阀1、2以及连接杆、上膜片、泵体组成上泵腔;簧片阀2、3以及连接杆、下膜片、泵体组成下泵腔;进口管与被抽容器相连通;出口管与大气相连通;动铁与连接杆固定连接。动铁随着线圈中励磁电流的变化而带动膜片往复运动,使上下泵腔体积变化,同时簧片阀根据其两侧压差进行开启与关闭,从而实现连续抽排气。
3 仿真模型建立
3.1 簧片阀运动模型
簧片阀的力平衡方程为:

式中:M—簧片阀等效质量;y—阀位移;y0—阀预紧位移;k—簧片
阀刚度;Ft—气动力;C—阻尼系数。簧片阀结构,如图2所示。
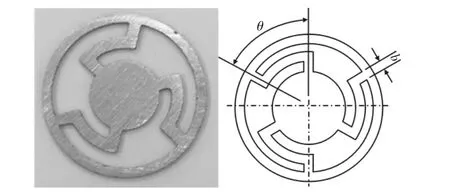
图2 簧片阀结构Fig.2 Structure of Reed Valve
首先,当簧片阀分别处于开启与关闭的状态时,所受到的气动力不相同,可表示为分段函数:
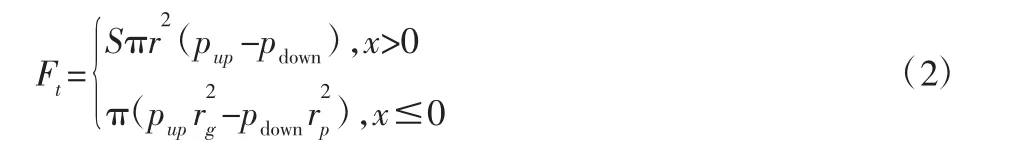
式中:S—面积系数;rp—簧片阀内盘半径;rg—通流孔半径。
为保证簧片阀的反向截止性能良好,使簧片阀内盘直径大于通流孔直径,从而使开启簧片阀所需压差大于开启后所需压差,因此在簧片阀开启初期,会产生高压侧到低压侧的气流脉冲,使簧片阀位移迅速增加。
其次,由于式(1)中只需用到簧片阀刚度和等效质量这两个参数,而未涉及簧片阀具体结构参数,不利于簧片阀后期结构优化。因此选择簧片阀的曲梁宽度、角度以及厚度作为结构变量,建立簧片阀刚度和等效质量与结构参数之间的关系式。
根据曲梁弯曲理论,簧片阀刚度k与厚度h及曲梁宽度b、角度 θ(rad)之间存在如下关系[10]:

式中:α—结构常数,f(θ)可由三次项逼近得到:

式中:β0~β3—结构常数。
现采用有限元法,固定曲梁宽度为1mm,厚度为0.15mm,改变曲梁角度为 60°,70°,80°,90°计算出簧片阀四种结构的刚度。再通过插值法得到结构常数:αβ0=-3.18e-18m5/N;αβ1=8.879e-18m5/N;αβ2=-7.353e-18m5/N;αβ3=2.733e-18m5/N。从而建立了簧片阀刚度与结构参数之间的关系式。
簧片阀等效质量M由内盘质量m1及部分的曲梁质量m2组成:

式中:γ—质量系数,取为0.5;由于内盘面积不变,故m1只与厚度
由于这里只讨论曲梁角度的变化范围为(60~90)°,故可以将曲梁角度θ0为60°,曲梁宽b0为1mm,厚度h0为0.15mm的簧片阀结构作为结构基准,得到如下关系式:
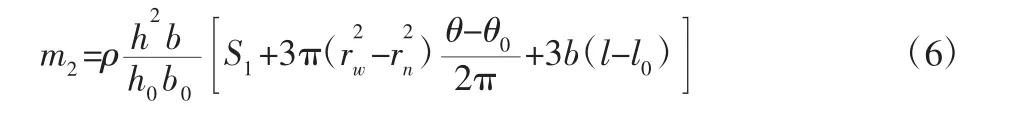
式中:材料为铍青铜(c17200),密度 ρ=8300kg/m3;rw—基准曲梁外半径;rn—基准曲梁内半径;S1—基准簧片阀曲梁总面积;l0—基准曲梁长度;l—曲梁长度。
为验证所建立的簧片阀刚度和等效质量与结构参数关系式的正确性,通过改变曲梁角度、宽度及厚度,分别利用有限元法和Catia建立仿真模型对以上两个关系式进行验证,如表1所示。其中簧片阀刚度的公式计算结果与有限元计算结果相比较,相对误差小于4%,而等效质量的公式计算结果与Catia计算结果几乎完全相同,从而验证了关系式的准确性,为后续簧片阀组的优化设计奠定基础。
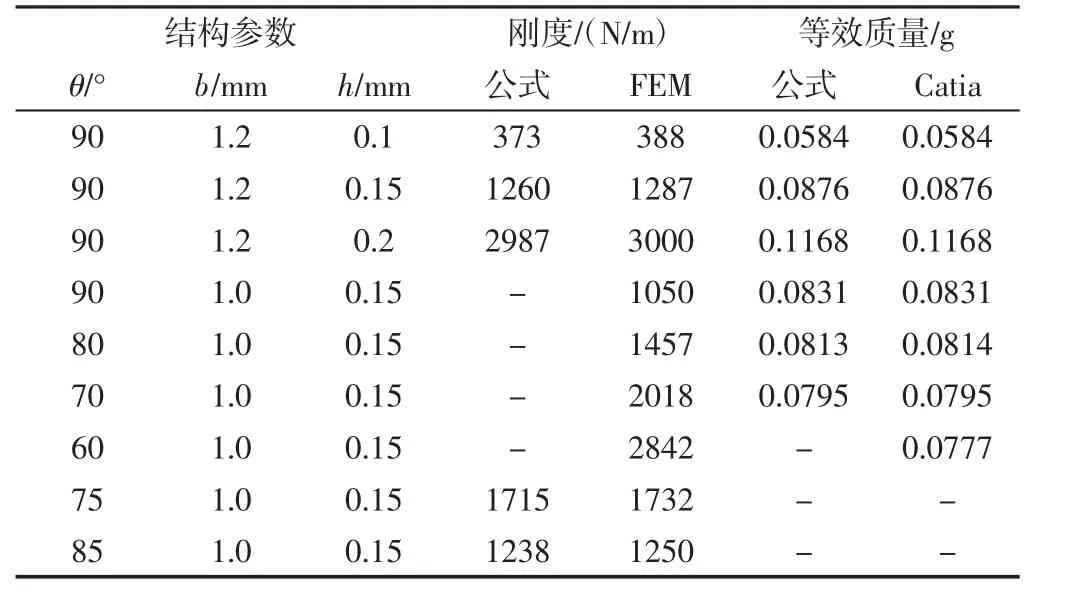
表1 簧片阀刚度与等效质量的公式验证Tab.1 Formula Validation of Reed Valve Rigidity and Equivalent Mass
3.2 泵腔气体质量及压强变化模型
被抽容器以及两个泵腔均会产生气体质量及压强的变化,而实际的进排气过程是非常复杂的,因此在对进排气的理论计算中,必须加以简化,以下计算公式将进排气过程视为绝热过程,且忽略腔体内压力脉动。由于上下腔体工作原理相同,因此只需将一个腔体作为研究对象。以下公式中以s、d为下标的分别表示进气口、排气口参数。由能量守恒方程推导可得:

并结合理想气体状态方程及绝热过程方程等基本微分方程,即可完成泵腔气体质量及压强变化模型的建立。
4 仿真模型实验验证及分析
4.1 实验验证
为验证仿真模型的准确性,搭建的真空度测试平台,如图3所示。

图3 真空度测试平台Fig.3 Vacuum Degree Test Platform
利用上位机调节电磁真空泵控制系统,使其在不同频率下稳定工作,运行结束后记录真空压力表所测得的真空度值。根据不同工作频率,分别在每个工作频率下测3组实验数据求平均值,并将其与仿真数据相比较,选取5种工作频率运行30s,得到实验与仿真的真空度对比,如图4所示。
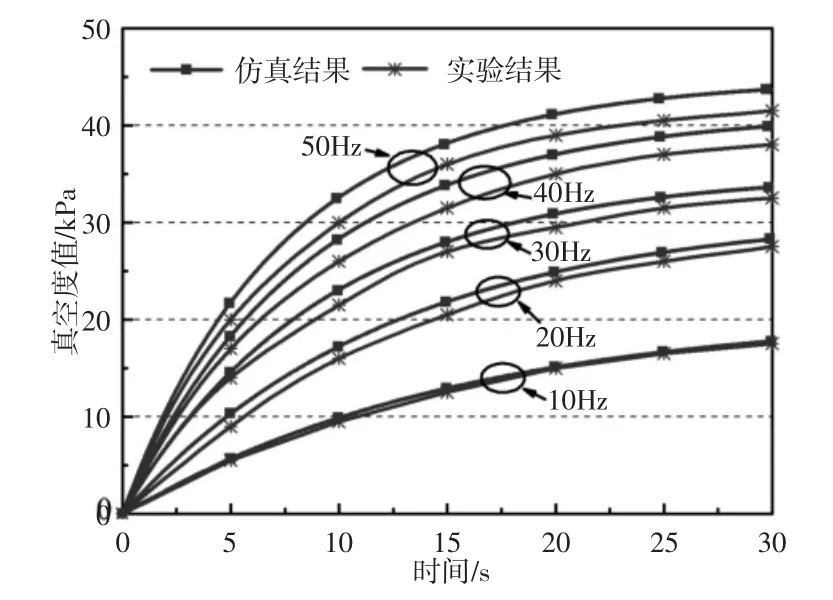
图4 实验与仿真真空度对比Fig.4 Comparison of Experimental and Simulated Vacuum Degree
由图4可知,仿真与实验的真空度最大相对误差为5.3%,可以验证模型具有一定的准确性。误差较大的原因为,本次实验设计的电磁真空泵在膜片及簧片阀安装方面的密封存在一定问题,存在气体泄漏、回流的情况,因此随着工作频率的增大,其相对误差相应增大,在低频时,模型吻合度更好。在后续的样机优化中会针对密封问题进行改进。
4.2 仿真模型分析
簧片阀作为电磁真空泵气体通断的关键部件,对泵的性能影响很大,当簧片阀刚度变化时,其位移曲线也会变化,从而导致泵的抽气性能也发生相应变化。若簧片阀刚度过大,会导致开启困难且关闭提前,影响气体通流能力;若簧片阀刚度过小,则会导致关闭延迟和密封不严,出现气体回流现象。因此选择合适的簧片阀刚度是至关重要的,尤其对于具有三个簧片阀的电磁真空泵而言,对抽气性能的影响更为严重。因此,针对提出的电磁真空泵,将簧片阀组结构参数作为优化变量进行优化能够较好地反映出电磁真空泵的结构特性,并能在更大程度上提升电磁真空泵的抽气性能。
在50Hz工作频率下,采用相同结构参数的簧片阀对电磁真空泵进行仿真,一个工作周期内簧片阀的位移曲线、泵腔压强变化曲线及动铁运动曲线,如图5所示。
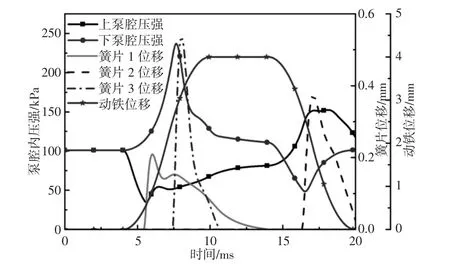
图5 泵腔压强及动铁和簧片阀位移Fig.5 Cavity Pressure and Displacement of Moving-Iron and Reed Valve
由图可作如下分析:
(1)当动铁由上端向下端运动时,由于上泵腔余隙容积远小于下泵腔余隙容积,两泵腔变化相同体积,上泵腔的压强减小速度大于下泵腔压强增大速度,因此簧片1比簧片3更早开启。又因为,簧片1上游初始压强及簧片3下游的压强均为大气压,因此簧片1两侧所形成的压差不超过1个大气压,而簧片3两侧所形成的压差超过1个大气压,因此簧片1开启位移远小于簧片3。由于簧片1开启位移小,所能通过的气体质量少,压差减小慢,因此其开启时间比簧片3更长;
(2)当动铁到达下端时,三个簧片均关闭,但上泵腔压强略微上升,下泵腔压强略微下降,说明此时有气体由下泵腔回流至上泵腔,其回流程度与簧片2两侧压差相关,通过样机实测确定压差与气体回流程度之间的关系;
(3)当动铁由下端向上端运动时,上泵腔压强增大,下泵腔压强减小,簧片2两侧压差为1个大气压左右,因此其开启位移大于簧片1位移,小于簧片3位移。
综上可知,簧片1开启位移过小,其簧片开启处为电磁真空泵的最小截面,很大程度地影响了电磁真空泵的抽气性能,因此需减小刚度以提升开启度;簧片2开启位移虽小于簧片3,但由于簧片2所承受反向压差大,对其反向截止性能要求高,因此刚度不可过小;簧片3所承受的正向压差大,反向压差小,因此其反向截止性能较为良好,仿真中所使用的刚度合适,但亦可适当减小刚度来提升抽气性能,刚度不可过小,会使位移过大而产生屈服形变。
5 优化设计
5.1 优化变量选择
以电磁真空泵在常用工作频率50Hz下工作30s所能达到真空度值最大为目标,优化三个簧片阀的结构参数。由于曲梁宽度和角度对簧片阀刚度的影响远小于簧片厚度对刚度的影响,且由试验可知曲梁宽度减小,角度增大可减小刚度,而刚度在一定范围内较小可有效提高抽气性能。因此为减少优化变量个数,选择将曲梁宽度固定为1mm,曲梁角度固定为90°,而只通过改变簧片阀组厚度来达到优化效果。
另外,需确定三个优化参数的范围,尽量减小变量范围,可减少计算量。通过仿真研究发现,当簧片阀组使用相同结构参数时,簧片阀1开启位移最小,而簧片阀2、3开启位移较大。因此认为簧片阀1应选用刚度较小的簧片阀,使开启位移增大;而簧片阀2对反向截止性能的要求高,因此刚度不可过小;簧片阀3开启位移较大,适当减小或不改变刚度均可。
由于初步仿真中所使用的簧片阀厚度均为0.2mm,经分析认为可以以0.15mm厚度作为基准厚度进行优化,为使优化更具有代表性,选择目标厚度与基准厚度的比值(Ki=h/h0,i=1,2,3)作为优化参数,可设置优化参数的范围为:K1∈[0.6,1.2];K2∈[0.8,1.4];K3∈[0.8,1.4]。
5.2 遗传算法
利用遗传算法优化簧片阀组厚度,选取种群个体数为20,变量个数为3,最大遗传代数为20,为使其精度达到0.01,设置各变量的二进制串长度为6位。通过选择、交叉、变异及重插入过程,不断更新种群中个体的基因,通过优胜劣汰,使种群中的个体适应度值更高,最终求得最优的簧片厚度组合及其对应所能达到的最大真空度[11]。
5.3 优化结果
经过遗传算法的优化,得到的电磁真空泵真空度优化收敛过程图,如图6所示。并确定优化变量分别为K1=0.91,K2=1.29,K3=1.13,即簧片厚度分别为 h1=0.1365mm,h2=0.1935mm,h3=0.1695mm时,30s内所能达到的真空度值最大,为66.9kPa。而在使用初始簧片组结构,即结构均为曲梁宽度1.2mm,曲梁角度60,簧片厚度0.2mm时,其在30s内所能达到的真空度值为41.9kPa。两者相比,在经过优化之后,电磁真空泵的真空度值同比增加37%,性能提升显著,说明了簧片阀组的固定结构参数及优化变量优化范围选择正确,也说明了优化具有意义。
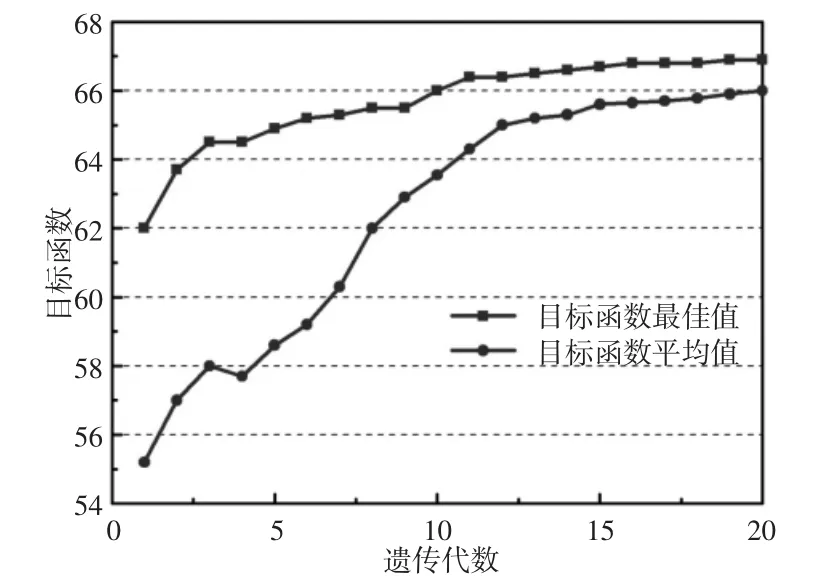
图6 真空度优化收敛过程Fig.6 Convergence Process of Vacuum Degree Optimization
6 结论
(1)提出了一种由电磁执行器直驱的两级串联膜片式真空泵,通过研究其工作过程建立了仿真模型,并进行了测试实验,验证了模型准确性,为样机的优化奠定了基础。(2)通过有限元法与插值法的结合,建立了簧片阀刚度与结构参数之间的关系式,并根据簧片阀结构建立了等效质量和结构参数之间的关系式,为样机的优化奠定了基础。(3)根据电磁真空泵的结构特性,选择三个簧片阀结构参数作为优化参数,并通过仿真分析确定了优化参数的范围,最后利用遗传算法完成了对初始样机的优化。通过优化,使电磁真空泵样机工作30s到达的真空度提升了37%,实现了抽气性能的有效提升,为电磁真空泵的后续研究提供参考。

