水声传感器网络中时钟漂移率跟踪方法

刘 迪，武岩波，朱 敏，李 栋

(1. 中国科学院声学研究所海洋声学技术中心，北京100190；2.中国科学院大学，北京100190；3. 北京市海洋声学装备工程技术研究中心，北京100190；4. 中国科学院声学研究所声场声信息国家重点实验室，北京100190)

0 引 言

基于水声通信技术的无线传感器网络作为海底观测网的重要组成部分，在维护国家海洋权益、开发和保护海洋资源方面有重要意义，在民用、军用海洋信息开发领域具有巨大的发展潜力，吸引了大量学者进行研究[1]。时钟同步是水声无线网各个节点协同观测的关键技术，对于某些声学或地震信号传感器，在长期工作过程中需要保持较高的同步精度才能检测和分析地震、海啸等突发事件。另外，为节省传感器节点能量，延长水下无线传感网络的生命周期，大多数工作节点采用睡眠-唤醒机制[2]，因此水下授时显得更为重要。

一般来说，水下获取精确时间基准的主要方式有：(1) 利用原子钟等高稳定度时钟授时，但该方法主要有两个缺陷。通常授时精度越高的系统，功耗、体积也越大。2016年，Woods Hole实验室[3]实验中使用的原子钟能耗在几十毫瓦量级，与普通石英晶振微瓦量级能耗间存在较大差异，而现阶段水下固定平台主要依靠自身携带的电池供电，能量非常有限，能耗是系统设计要考虑的首要问题。另外这种方式的时间累积误差也是不断积累的，长期工作也必须通过其他方式校准。(2) 水下声波协议授时，这种方式通常通过已知精确时间的节点和需要进行时间校准的传感器节点进行水声信息交互，进而实现授时功能。水下声波协议授时是本文研究的主要内容。

传感器节点使用晶振产生本地时钟。在实际使用中，出于对降低成本的考虑，普遍使用频率准确度低和稳定性差的廉价晶体振荡器[4]。因制造工艺、温度等因素的影响，不同传感器节点晶振的输出频率会不同。节点时钟输出频率的差异称为时钟漂移率。若两时钟之间的时钟漂移率为α，意味着记录相同一段时间T，第一个时钟相对于第二个时钟记录的时间的偏差为αT。时钟漂移率的存在会导致本地时钟之间产生累积误差，称为时钟偏差[5]。这就要求授时协议要同时获得时钟漂移率和时钟偏差并进行补偿。

现已有多种针对陆地无线传感网络的授时算法[6-9]。其中参考广播时钟同步协议(Reference Broadcast Synchronization, RBS)算法[6]、洪泛时间同步协议(Flooding Time Synchronization Protocol,FTSP)算法[7]、无线精确时间同步协议(Wireless Precision Time Protocol, WPTP)算法[8]认为信号的发送和接收可以瞬时完成，(Timing-sync Protocol for Sensor Networks, TPSN)[9]没有考虑同步消息交换过程中时钟漂移率的影响，而水声通信带宽窄、通信比特速率低[10]、传播时延大，这些特点使许多用于地上传感器网络的授时协议不能直接应用于水下。

针对水下传感网络授时问题，研究者们做了一系列的研究，并取得了一些成果。2006年，Syed等[11]提出高时延时间同步(Time Synchronization for High Latency, TSHL)水声网络授时协议，第一个考虑了时钟漂移率在高时延授时过程中对授时误差的影响。2009年，Tian等[12]提出的Tri-message授时协议在TSHL算法开销方面进行了改进，通过3次时间戳交换过程修正时钟漂移率和时钟偏差。2012年，美国海军研究生院在TSHL授时协议的基础上考虑了信道多径对授时精度造成的影响[13]，并对授时过程进行了湖试实验，实验中时钟漂移率最小估计误差为 9×10-6s。以上研究中，水声授时协议的设计都基于授时过程中时钟漂移率为常数的假设。2016年，德国Evologics公司研制具有授时功能的S2CR Series Modem，并用其在地中海进行了授时实验[14]。实验中接收节点与发送节点之间的时间戳交换过程基于双程信息交换模型，接收节点计算并记录本地时钟偏差随时间的变化情况。该水声授时实验进行的时间很短(5～10 min)，并没有对时钟漂移率进行修正，也未进行时钟漂移率的长期变化特性的观察和研究。然而，在实际应用中，温度是影响时钟输出频率最明显的因素。传感器节点若长时间运行在水下，时钟漂移率受周围环境的影响会产生变化。Sathiya等[15]为观察时钟漂移率变化特性与时间和温度的关系进行了实验并得出结论：各个节点的时钟受到外部条件的影响，时钟漂移率随温度和时间的变化呈现非线性特征。实时估计和补偿时钟漂移率，能提高授时精度并减少授时次数。然而，时钟漂移率的测量会受到噪声的影响，同时消息包的传输延时也具有不确定性，这些因素都会导致待同步节点无法对标准时钟节点进行准确测量和估计。

卡尔曼(Kalman)滤波算法可以较好地解决实时状态估计问题，但常规Kalman算法需要根据经验或先验知识设定滤波参数。Sage-Husa算法在Kalman滤波算法的基础上，可实时更新滤波参数来提高估计精度[16]。文献[17]中采用一阶线性模型对时钟漂移率进行建模，并利用Kalman滤波对时钟状态进行估计和纠正，但该文献未对变时钟漂移率进行分析和研究。Yang等[18]提出使用交互式多模型Kalman滤波对时钟漂移率进行估计，但处理的是高斯白噪声数据，滤波参数固定，且时钟漂移率的变化模型的提出也没有实验数据支撑。据我们所知，目前在水声通信授时领域，没有相关研究考虑长时时钟漂移率变化对授时误差的影响。

针对现有水声授时协议未考虑授时后时钟漂移率变化的问题，本文在对时钟模型深入分析的基础上，提出一种适用于水声传感网络授时的时钟漂移率估计方案。为了找到合适的时钟漂移率变化模型，本文首先根据海试实验数据确定时钟漂移率的漂移范围和趋势，使用多个模型描述其变化行为；其次，在使用现有授时协议仿真水声通信过程获得时钟漂移率的基础上，使用交互式多模型 Kalman滤波方法对变时钟状态向量进行估计，并在滤波过程中采用 Sage-Husa自适应方法动态确定滤波参数，提高估计精度；最后，通过仿真实验验证了该授时方法的有效性。

1 授时过程基本模型

本文假设场景中有一个标准的时钟节点(即已同步节点)A和一个为待同步的本地时钟节点B。假设t代表标准时间，T代表节点B的本地时间，α和b分别代表本地时钟的时钟漂移率和时钟偏差。节点的本地时间和标准时间之间的关系可以表示为

时钟同步的基本思想是节点间通过数据交换的方式，估计时钟漂移率和偏差，修正本地时钟，使得本地时钟与标准时钟保持同步[19]。

两节点间数据交换示意图如图1所示。B发送同步消息，该消息包含其发送时间T1，经过时间Δt后，信息到达A，A记录下该信息到达时间t2；两节点交换收发角色，A向B发送同步信息，信息中包含其发送时间t3和上次接收时间t2，经过时间Δt后，信息达到B，B记录下该信息到达时间T4。这样，B共获得4个时间戳，时钟偏差计算可得：

由式(3)可知，授时误差和时钟漂移率及数据包交换时间成比例增长，数据包交换时间越长，由时钟漂移率α导致的授时误差e越大。若能较好地对时钟漂移率进行补偿，就能很大程度提高授时精度。

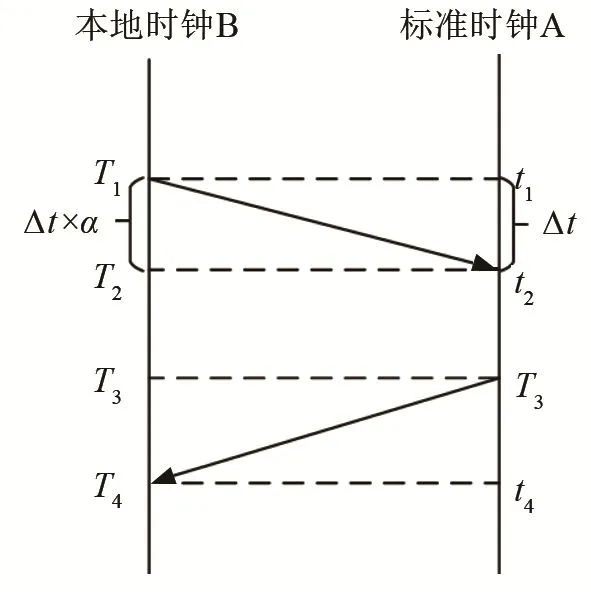
图1 两节点间数据交换示意图Fig.1 Schematic diagram of data exchange between two nodes

2 基于现有水声授时协议的时钟漂移率计算方法

现阶段，水声通信领域较为经典的授时协议主要包括 TSHL[11]和 Tri-message[12]等。其中，TSHL采用 25个时间戳消息线性拟合的方式估计时钟漂移率，估计精度高，但耗能高。Tri-message采用3次消息交换估计时钟漂移率，该方式估计精度较TSHL低，但耗能低。本文提出了组合通信方案，在保证一定精度的同时，多数情况下采用两种授时方式组合计算时钟漂移率。本文中采用两种方式组合使用的方式，示意图如图2所示。

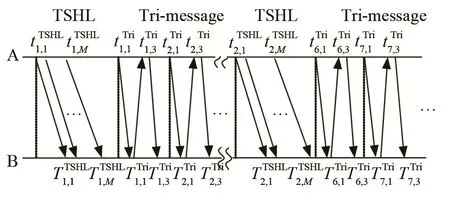
图2 时钟漂移率组合方式计算方法示意图Fig.2 Schematic diagram of combined clock skew calculation method

时钟漂移率具体计算方式如下：

(1) TSHL方法：标准节点A向待同步节点B连续发送M个标准时间信息(k表示第k次TSHL授时过程，k=1 , 2,⋅⋅)，节点 B 根据接收到的M个消息时的本地时间戳和相应的标准时间戳，在以下数据点进行线性拟合：，得到本地时钟B的时钟漂移率。

(2) Tri-message方法：采用3次信息交换，节点B获得6个时间戳后，用式(4)估计本地的时钟漂移率：

式中：l表示第l次Tri-message授时过程。本文假设使用 TSHL方式估计时钟漂移率的时间间隔为I1，使用Tri-message的时间间隔为I2，I1、I2的单位为h。TSHL与Tri-message方式交替使用，具体通信过程图示如图 2所示。参数满足M=25，2,⋅⋅)。

对3种授时方法的精度和耗能方面进行分析：授时方法的耗能主要来自于对时钟漂移率α的估计，α由接收节点对时间戳消息线性拟合得到。利用文献[12]中的方法对 TSHL、Tri-messgae和本文采用的组合授时方法进行线性拟合算法复杂度分析，结果如表1所示。

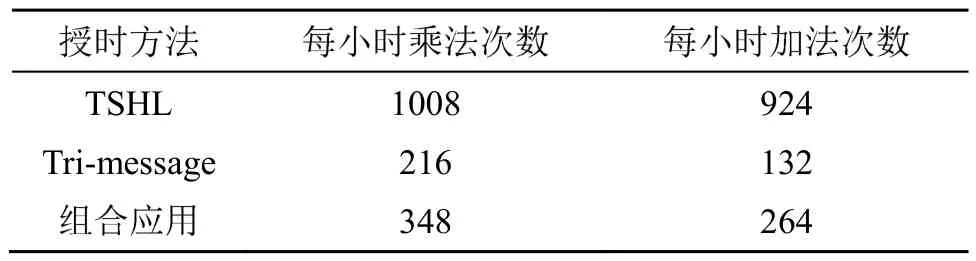
表1 不同授时方法线性拟合计算复杂度Table 1 The complexities of linear fitting computation of different time synchronization methods

授时精度方面：由于TSHL授时方法发送的时间戳数量多，接收节点可以利用到的时间信息较为丰富，利用该授时方法得到的授时误差较小，而Tri-message授时方法利用的时间戳数量少，该授时方法误差较大，本文采用的组合应用方法将两种授时方案结合使用，在保证一定授时精度的同时减少耗能。对24个大小不同的时钟漂移率α，3种不同授时方法的发送端分别向接收端发送不同数量时间戳，接收端通过对接收到的时间戳消息进行线性拟合对α进行估计，每次估计出的α值是100次实验的平均值。表2是通过上述3种方法计算的授时方法精度误差均值对比表。

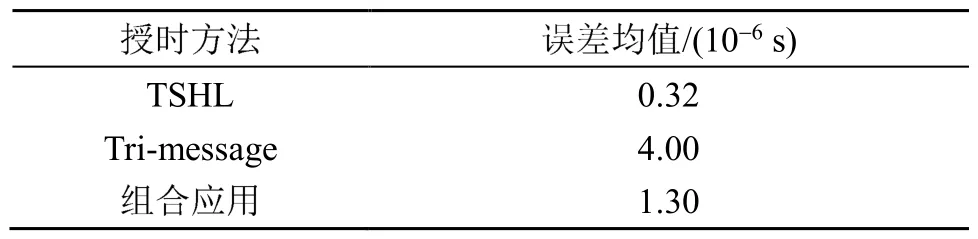
表2 不同授时方法授时误差均值比较Table 2 The average errors of different time synchronization methods

由表1和表2可知，本文采用的组合授时方法在保证一定同步精度的同时减少了耗能。

3 变时钟漂移率估计方法

通过使用第2节描述的方法获得时钟漂移率，本文采用文献[18]中提出的估计方法，将其作为交互式多模型Kalman滤波的输入。另外，为了更准确地追踪时钟漂移率的变化，提高授时精度，本文在滤波过程中采用Sage-Husa算法实时更新滤波参数。

时钟漂移率随时间和温度变化的情况是复杂的，不会保持在同一种状态。本文使用多个模型描述时钟漂移率的变化。交互式多模型Kalman滤波算法中的多个滤波器对应于不同的模型，各模型描述不同的时钟漂移率的变化特性。设时钟离散状态向量c(k) =[θ(k)α(k)ρ(k)]T，其中，θ(k)表示时钟偏差，α(k)表示时钟漂移率，ρ(k)表示时钟漂移率变化率；使用恒定加速模型表征时钟漂移率的变化情况：

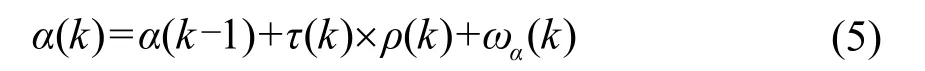
式中：τ(k)表示采样间隔，ωα(k)表示噪声量。将时钟模型改写为矩阵向量表达式：

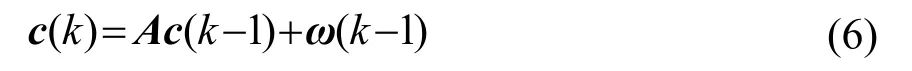
式中：A为状态转移矩阵，ω为系统噪声向量。定义z(k)=α(k)为观测值，则观测模型可写为

式中：H为观测矩阵，ν(k)为观测噪声。ω和ν分别表示系统噪声和测量噪声，其协方差矩阵分别为Q和R。并设模型间转移矩阵为马尔科夫矩阵。对具有n个模型的系统，系统的状态方程和测量方程如式(8)和(9)所示：

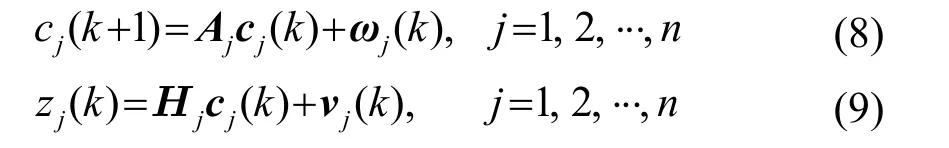
使用交互式多模型估计时钟漂移率的过程如图3所示。

图3 交互式多模型Kalman滤波结构图Fig.3 Structure diagram of interactive multi-model Kalman filter

交互式多模型估计时钟漂移率主要分为3个步骤：输入交互、Kalman滤波和输出组合。

(1) 输入交互。计算匹配模型mj(k)的混合初始条件。mj(k)表示模型j在k时刻的概率，pij表示模型i到模型j的状态转移矩阵。模型预测概率和模型转移概率µi/j分别表示为

输入交互后的混合输入表示为

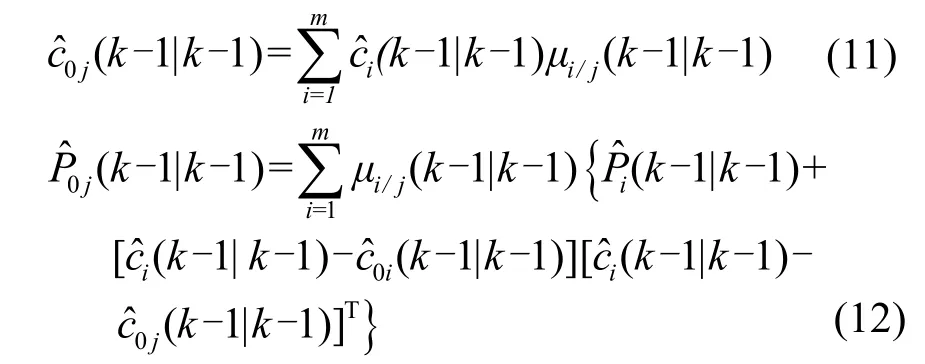
(2) Kalman滤波。对模型j，将及z(k)作为输入进行Kalman滤波。在滤波过程中，z(k)是通过仿真现有水声授时协议的时间戳交换过程计算得到，并不符合经典 Kalman滤波假设的高斯的统计特性，且实际应用系统中系统模型一般是复杂的，噪声统计特性往往是未知而且时变的，先验数据会因此失去意义，想获得噪声统计特性十分困难。于是，本文采用在工程上广泛应用的Sage-Husa方法[16]，根据新获得的观测数据，在线估计出系统噪声特性，实时更新滤波参数Q和R，保证滤波稳定性，提高滤波收敛速率和效果。更新参数过程如下：

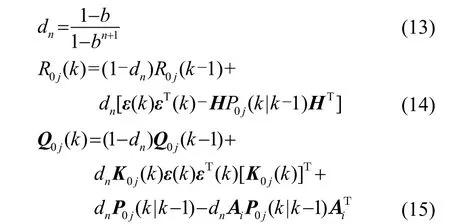
式(13)～(15)中：b为遗忘因子；ε(k)为信息矩阵。

(3) 输出组合。基于似然函数计算k时刻模型mj的动态权重Sj(k)，并由此获得多模型滤波器的输出。对m个模型，首先分别计算模型mj的更新概率：

则最终输出的状态估计可表示为

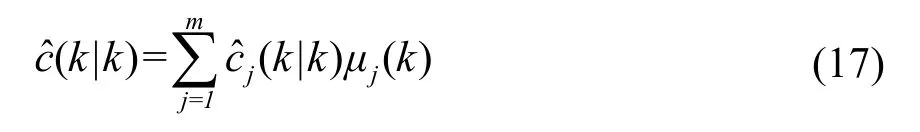
采用该滤波算法可以得到变时钟漂移率模型的估计结果，用估计结果对时钟漂移率进行修正和补偿，之后可进行双程信息交换，修正时钟偏差。

4 仿真结果和分析

2013年7月，在海南某浅海海域采集了一天内的温度变化数据。由这些数据可得水下节点晶振输出频率随时间的变化曲线，由温度变化导致时钟漂移率产生的变化最大可达10-5s左右，如图4中虚线所示。图4中阶梯状的变化曲线表示现有水声授时协议对变时钟漂移率的处理：每一次授时后不考虑时钟漂移率的变化(假设一天内进行了 6次授时过程)。这会导致在时钟漂移率变化程度较为明显时，授时误差大幅增加。极端情况下，一天时间内由时钟漂移率变化造成的授时误差可达20 s，整个时钟无法使用。

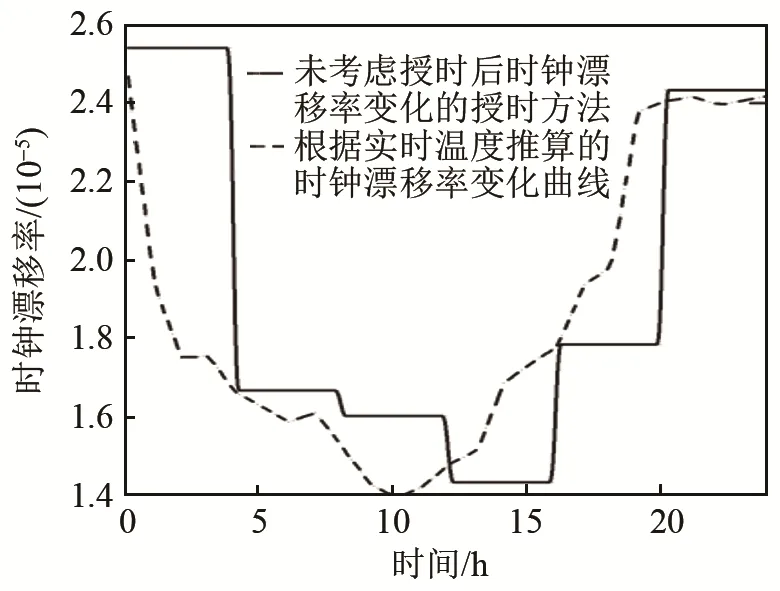
图4 时钟漂移率的海上试验数据推算结果(虚线)及现有授时模型的处理结果(实线)Fig.4 The clock skew calculated from sea test data (dashed line) and the clock skew processed by existing time synchronization model (real line)

将根据实时温度推算的时钟漂移率变化曲线作为参考曲线，本节对提出的变时钟漂移率估计方法进行了模拟仿真分析。估计方法使用 Sage-Husa自适应Kalman滤波对数据进行处理，可根据输入的数据实时估计系统的过程噪声和测量噪声协方差矩阵，追踪输入数据的变化并对滤波器参数进行修正，以此提高滤波效果。另外，用方法1表示基于现有水声授时协议的时钟漂移率估计方法，具体计算方案与参数设置详见第2节。方法2表示在通过现有水声授时协议估计时钟漂移率的基础上，使用不调整滤波参数的多模型Kalman滤波时钟漂移率估计方法。本节对提出的估计方法与方法1和方法2进行了对比实验。

图 5和图 6分别表示使用参数不变的标准Kalman滤波方法(简称：标准Kalman滤波)和Sage-Husa自适应滤波方法的滤波结果对比图和累计误差对比图。设时钟漂移率真实变化模型如图5中红色实线所示，对该模型的观察时间为200 s，前100 s模型噪声为高斯白噪声，后100 s用混合高斯噪声仿真滤波的Q、R参数的改变。之后分别用参数不变的标准 Kalman滤波和 Sage-Husa 滤波方法对该模型进行滤波处理。

图5 两种滤波方法估计结果对比图Fig.5 Comparison of estimation results of two filtering methods

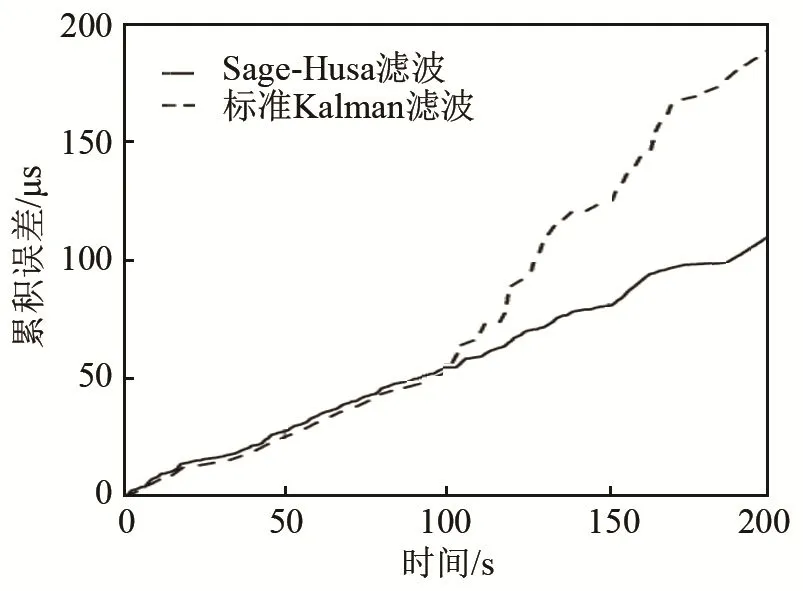
图6 两种滤波方法累积误差对比图Fig.6 Comparison of accumulation results of two filtering methods

由图5和图6可以看出，使用参数固定不变的标准Kalman方法在噪声发生变化的情况下，滤波效果不如滤波参数可以自适应调节的滤波方法。

之后，对实验数据进行分析、处理及仿真。仿真实验中，设待同步节点初始时钟偏差10 µs，时间戳接收抖动分布由均值为 0、标准差为 15 µs的高斯分布引入，时钟的仿真粒度为1 µs，标准节点发送时间戳的时间间隔为1 s。

图7显示的是一天内，采用本文授时算法、方法1和方法2对变时钟漂移率的估计情况。由图7可以看出，在0～4 h、8～12 h、16～20 h等时钟漂移率出现较大程度变化的时间段，可以对其进行较好的估计和跟踪，本文提出的时钟漂移率计算方法结果表现优于方法1和方法2。方法1因能耗因素，在大多数情况下采用 Tri-message授时方法计算时钟漂移率，精度不高，且该方法单次授时结束后，并未考虑授时后时钟漂移率的变化情况；方法2假设进行Kalman滤波的滤波参数是固定的，这在已知噪声分布的情况下是可以的，但本文授时方法的时钟漂移率的值是通过仿真现有水声授时协议过程得到的，噪声分布并不是已知的，故方法2只能跟踪时钟漂移率变化的大致趋势，对时钟漂移率模型判断不准确，授时误差较大。图8给出了3种时钟漂移率估计方法累积授时误差变化图。这3种方法的授时误差随着时间的推移都会有不同程度的增加，采用本文提出的时钟漂移率估计方案对其进行估计和修正，授时精度最高，一天内现有授时协议累积的授时误差大约为本文提出的估计方法的1.5倍。图9给出了3种时钟漂移率估计方法结果的均方误差变化图。本文使用的估计方法与其他两种授时方法相比，误差增加速度最小，一天内的授时均方误差可由3.0×10-9s2降低到5×10-10s2。

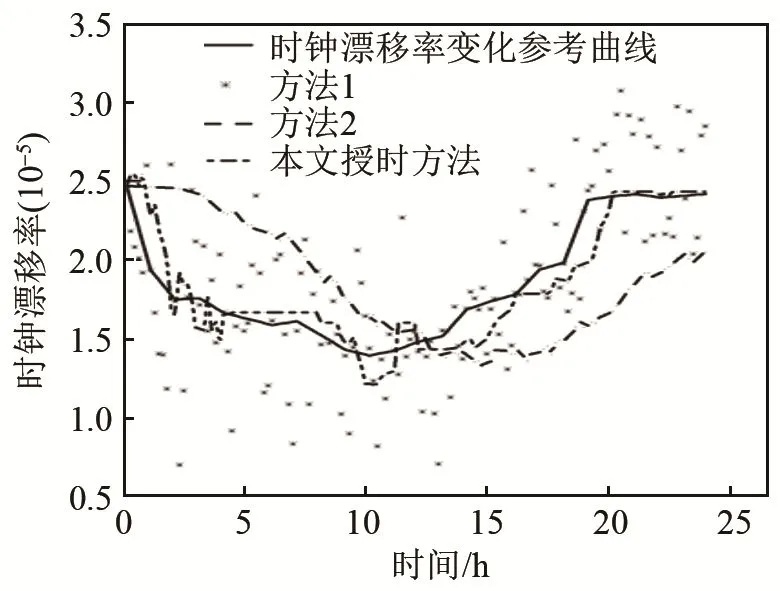
图7 3种授时方法估计时钟漂移率的对比图Fig.7 Comparison between the clock skews estimated by three time synchronization methods

图8 3种授时方法累积授时误差对比图Fig.8 Comparison between the accumulated timing errors of three time synchronization methods

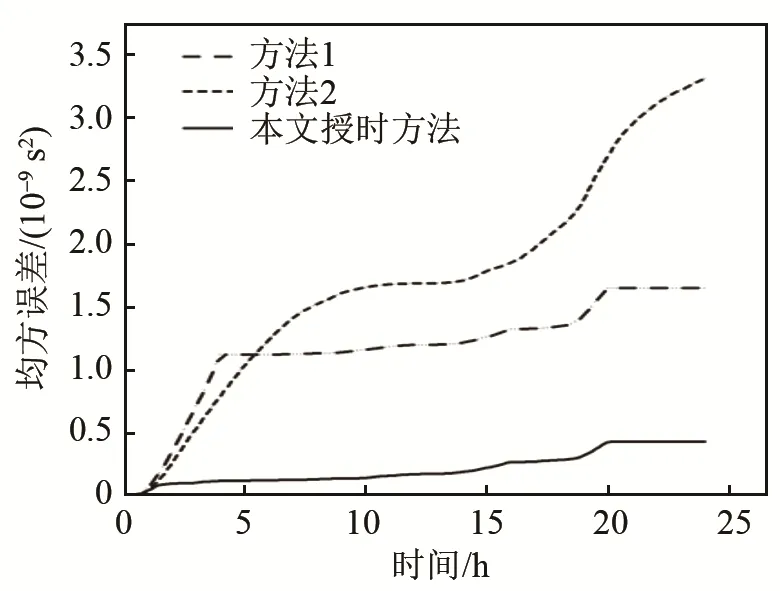
图9 3种授时方法的均方误差对比图Fig.9 Comparison between the mean square errors of three time synchronization methods

综上所述，该算法能实现对变时钟漂移率进行预测和追踪，有效地提高水声通信节点的授时精度，具有较好的性能。

5 结 论

本文针对长时时钟漂移率随周围环境产生变化的问题，提出了一种适用于水下传感网络的时钟漂移率跟踪算法。本文在水声通信授时领域提出，在进行水声授时的同时考虑长时变时钟漂移率对授时精度产生的影响。使用多个模型描述时钟漂移率的变化，在利用现有水声授时协议计算获得时钟漂移率的基础上，采用交互式多模型Kalman滤波对变时钟漂移率进行估计，并在滤波过程中实时更新滤波参数，提高时钟漂移率估计的准确性，进而提高水下节点的授时精度。仿真结果表明，该方法与现有的授时方法相比，累积授时误差小，授时均方误差可从 3.0×10-9s2降低到 5×10-10s2。