傅立叶变换下色散光纤信号的强度和相位计算*
苏红梅
(罗定职业技术学院,广东 罗定 527200)
目前,学者们关于在波长λ≈1.55 μm下运行的光纤通信系统的研究比较多,因为在该波长范围内光纤损耗较低.但是对于这个波长的标准单模光纤信号[1],会表现出明显的色散现象,从而产生对传输带宽的限制.为了减少信号在传输过程中出现的色散现象,笔者拟建立一个一般的小信号关系,利用傅立叶变换得到光纤输出处的强度和相位的调制情况,并且在光纤输入端,对于允许的、任意的输入强度和相位调制(或噪声)都有效.
1 傅立叶变换简介
傅立叶变换是一种分析信号的方法[2-5],是将一个时域非周期的连续信号转换为一个在频域非周期的连续信号.通过它可以分析信号的成分,也可以将这些成分合成信号.许多波形可作为信号的成分,如正弦波、方波和锯齿波等.
令f(t)是t的周期函数,若t满足狄里赫莱条件:函数在任意有限区间内连续,或只有有限个第一类间断点(当t从左或右趋于这个间断点时,函数有有限的左极限和右极限);在一个周期内,函数有有限个极大值或极小值;函数在单个周期内绝对可积.则将如下积分运算称为f(t)的傅立叶变换:
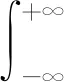
其中F(ω)称为f(t)的像函数,f(t)称为F(ω)的像原函数.将如下积分运算称为F(ω)的傅立叶逆变换:
傅立叶变换在物理学、组合数学、信号处理、密码学和声学等领域都有广泛的应用.在信号处理中,傅立叶变换的典型用途是将信号分解成频率谱,显示与频率对应的幅值大小.
2 光纤输出处光场的强度和相位的计算
首先介绍强度和相位调制信号在色散介质中传播的理论,利用傅立叶变换得到强度和相位的具体表达式.这里主要考虑的是具有平均光发射的单模激光二极管[1,6-10]频率ωth、相位φin(t)和强度(光学功率)Sin(t).令Ein(t)表示输入的场振幅,
(1)
则(1)式对应的傅立叶变换为

(2)
通过光纤传播的光信号可以用传播项e-jβL来表示,其中L为传播光纤的长度.相位常数β(忽略损耗)在ω=ωth附近的展开表达式为
(3)
其中
(4)
其中λ和c分别表示光的波长和传播速度.
如果由(3)式定义的β来确定传播项e-jβL,并应用到(2)式的输出信号中,那么输出光纤信号在频域里的复合场强度的表达式为
Eout(jω)=Ein(jω)e-jβL.
(5)
将(3)式代入(5)式,得到
(6)
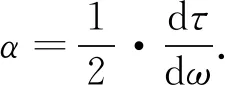
(7)
再将(6)式代入(7)式,得到
(8)
又因为
(9)
而Ein(j(ω+ωth))的时域傅立叶变换为
(10)
则(10)式的傅立叶逆变换为
所以
(11)
将(11)式代入(9)式,化简后的结果再代入(8)式,得到
(12)
为了方便起见,忽略相位β0L和群延迟τL,因为这2项只产生时延的载波信号和调制信号,对信号的失真没有影响.结合(4)式,进一步得到(12)式中的色散参数表达式:
(13)
将(13)式代入(12)式,则光纤输出处的振幅表达式为
(14)
其中:Sout(t)和φout(t)分别为光纤输出处场强的强度和相位;ΔE(t)为色散产生的附加场振幅,其表达式为
(15)
在小信号分析理论中,ΔE(t)假定为非常小,
|ΔE(t)|≪|Ein(t)|.
(16)
根据(14)式,光纤输出强度可以表示为
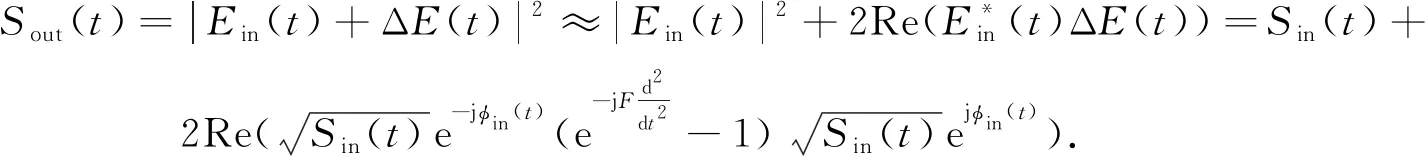
(17)
这里的计算利用了(15)和(16)式,略去了高阶小量.通过相同的估算和相似的步骤,可以推导出光纤输出相位的表达式为
(18)
(17)和(18)式分别是描述信号通过色散光纤传播后的光场强度和相位的一般方程.只要色散产生的附加场振幅ΔE(t)远小于输入场振幅Ein(t),那么(17)和(18)式对于任意的输入强度Sin(t)和相位φin(t)都是有效的.
3 结语
在输入信号为小信号的前提下,反复运用傅立叶变换和逆变换推导出光纤输出处的强度和相位的一般表达式.这可以给如何降低信号传输过程中的色散影响等类似工作提供参考.

