基于多核学习的风格正则化最小二乘支持向量机*

沈 浩，王士同

1.江南大学数字媒体学院，江苏无锡 214122

2.江南大学江苏省媒体设计与软件技术重点实验室，江苏无锡 214122

1 引言

由于支持向量机[1]（support vector machine，SVM）的提出及其相关理论的发展，核方法成为一种可以有效处理非线性可分数据的方法。由于分类算法的性能很大程度上取决于数据的表示，而核方法利用相对简单的函数运算将样本映射到更高的维度,避免了特征空间的设计以及特征空间中复杂的内积计算，得益于此，核方法被应用到机器学习的众多领域中[2-4]。

然而在一些样本分布不平坦、特征异构或不规则的数据中，仅利用了单个特征空间的单核方法表现不佳；而且由于不同核函数具有各自的特性，即使在相同的应用场合下，使用不同核函数取得的效果可能差别很大，从而使得核函数及其参数的选择对于算法的性能具有重要影响。由于仅使用单个核函数并不能满足一些实际应用场景下的需求，因此产生了将多个核函数进行组合的多核学习方法[5]。

通过多核学习产生的组合可以是同一种核函数取不同参数下的组合，也可以是多个不同种类核函数的组合[6]。经过多年研究，相较于仅使用单个核函数的方法，多核学习在数据降维[7]、文本分类[8]、领域适应学习[9]等多个领域内已被证明是一类灵活性更强、可解释性更高而且性能更优的基于核的学习方法[10-11]，并且研究出了多种针对支持向量机的多核学习算法及性能优化方法。

虽然多核学习算法充分结合了不同核函数对于数据的映射能力，但其本质上仍然是仅利用了如相似性、距离等在内的样本的物理特征，并没有考虑到现实情境中存在的风格化数据集内隐含的信息。在实际应用中，除代表的内容信息之外，数据集中往往包含着各种风格信息，并且具有相同风格的样本往往会以组的形式存在。例如，对图1（a）中的字母数据存在两种划分形式，分别为图1（b）中所示的按内容划分和图1（c）中所示的按字体划分。此处每种字体被视为一种风格，此类数据被视为风格化数据。现实情境中更多此类的例子包括：语音数据集中来自不同地域或个体的样本中往往包含着不同的口音和声调等特征，人脸图像样本中包含着不同的姿态特征等。对风格化数据中所包含的除物理特征之外的风格信息进行挖掘及对于算法性能的提高具有重要意义。

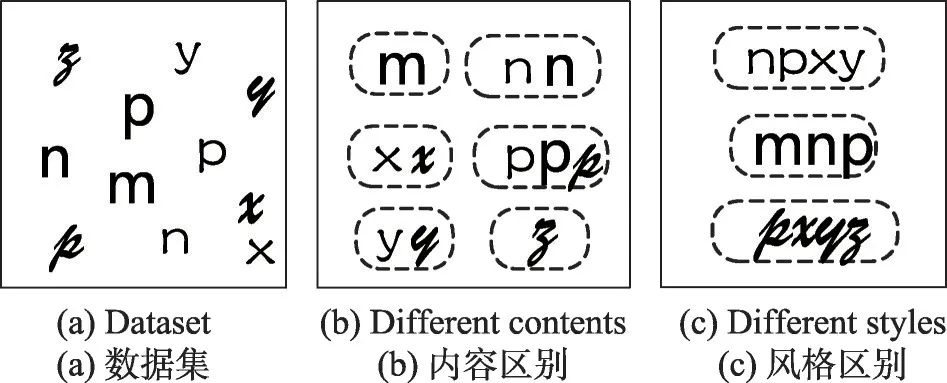
Fig.1 Example of stylistic data图1 风格化数据示例

为挖掘数据的风格信息，学者们进行了许多研究。文献[12]提出的二阶统计模型应用在数字识别问题中，但仅对服从高斯分布的数据效果较好，导致算法的适用情景受到较大限制。文献[13]提出的双线性判别模型在行为识别数据中取得了良好的效果，但算法计算过程开销较大。文献[14]提出的域贝叶斯算法改进了朴素贝叶斯算法，对样本组中的风格信息进行识别，但需要预先为算法指定一种明确的数据分布类型，然而现实情景中数据的分布情况常常是较为复杂且较难事先明确的。文献[15-16]提出的算法利用单种映射挖掘了样本的风格信息并在回归和分类问题中取得了优良的效果，但对样本物理特征的利用有限。文献[17]提出的挖掘样本历史信息的时间序列风格模型以及文献[18]提出利用了用户的年龄和性别信息的双层聚类模型，在无监督问题中有效利用了数据中的风格信息，但算法仅针对特定的领域，且利用的风格信息有限。

受以上学者工作启发，本文提出基于多核学习的风格正则化最小二乘支持向量机（style regularized least squares support vector machine based on multiple kernel learning，MK-SRLSSVM）对样本点之间的物理相似性及样本中隐含的风格信息进行挖掘和利用。算法在利用了各基本核函数对于数据映射的物理特性来表达样本之间的相似性之外，使用风格转换矩阵表示并挖掘数据集中包含的各种风格信息，并将其考虑进目标函数中。在训练过程中使用交替优化策略，除分类器参数之外，同时更新风格转换矩阵，并且使用挖掘出的风格信息对核矩阵进行同步更新。为在预测过程中利用训练得到的样本风格信息，在传统多核最小二乘支持向量机的预测方法之上添加了两个新的预测规则。由于在训练和预测过程中都有效利用了样本中包含的风格信息，在多数风格化数据集的实验中显示出MK-SRLSSVM较新近以及经典的多核支持向量机算法的有效性。

2 相关算法及概念

2.1 多核学习

设x和z为样本向量，Φ为从输入空间到特征空间的映射，若有函数k(·,·)可使：

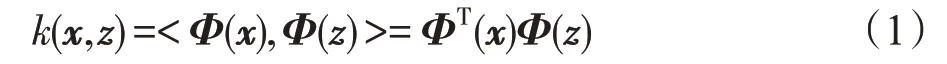
则称k(·,·)为核函数。

多核学习期望通过对不同的核函数进行组合，以取得更佳的映射性能，组合的方式有多种[5]。

本文使用如下求组合核函数的方式，设有M个基本核函数ki(·,·)，μi为每个基本核函数的权重系数，则合成核函数为：

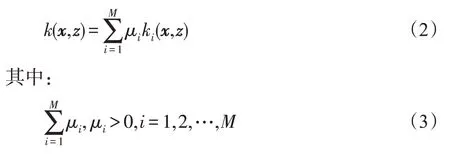
由Mercer理论可知，通过以上方法生成的组合核函数仍满足Mercer条件。

2.2 基于多核学习的最小二乘支持向量机

设D={(x1,y1),(x2,y2),…,(xn,yn)}为训练样本集合，xj∈Rd为其中的一个样本，yj∈{+1,-1}为xj对应的标签。Suykens[19]在支持向量机（SVM）的基础上提出的最小二乘支持向量机（least squares support vector machines，LSSVM）的目标函数为：

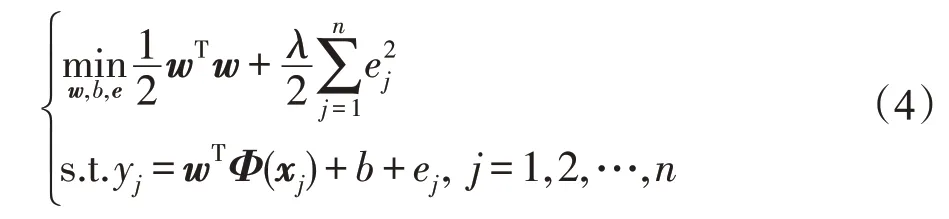
其中，Φ(xj)为映射到高维后的样本；w、b为分类超平面参数；ej(j=1,2,…,n)为误差项；λ为正则化参数。

对式（4）引入拉格朗日乘子α，由Slater约束规范进一步可得其对偶形式：

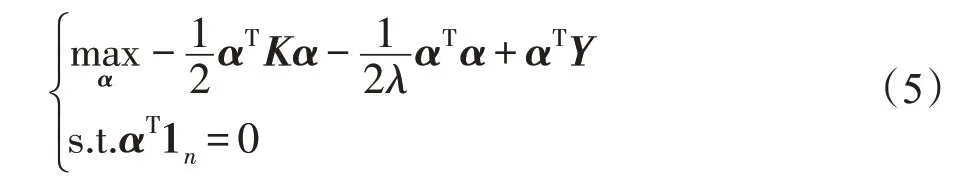
其中，K∈Rn×n为核矩阵，通过求解式（5）可得:

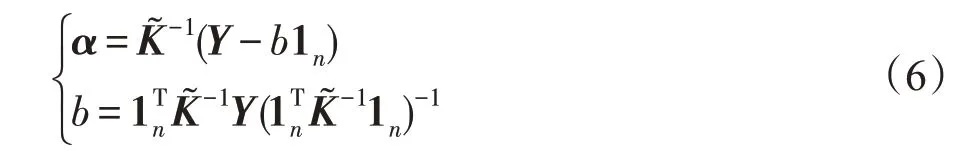
对式（5）中的核矩阵K引入式（2）和式（3）的多核学习方法[20]，可得基于多核学习的最小二乘支持向量机（least squares support vector machine based on multiple kernel learning，MK-LSSVM）：

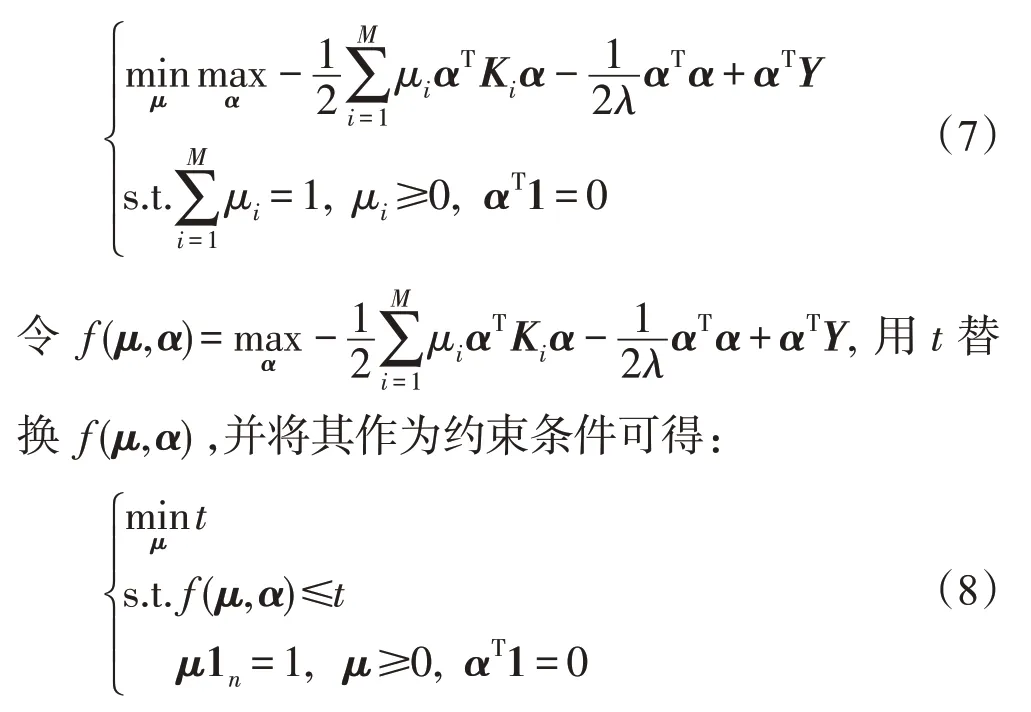
此式为半无限线性规划（semi-infinite linear program，SILP）问题，可用现有的很多成熟的优化工具包来解决，并由2.3节的算法1得出μ和{w,b}。MK-LSSVM对未知样本x的判别式[21]为：

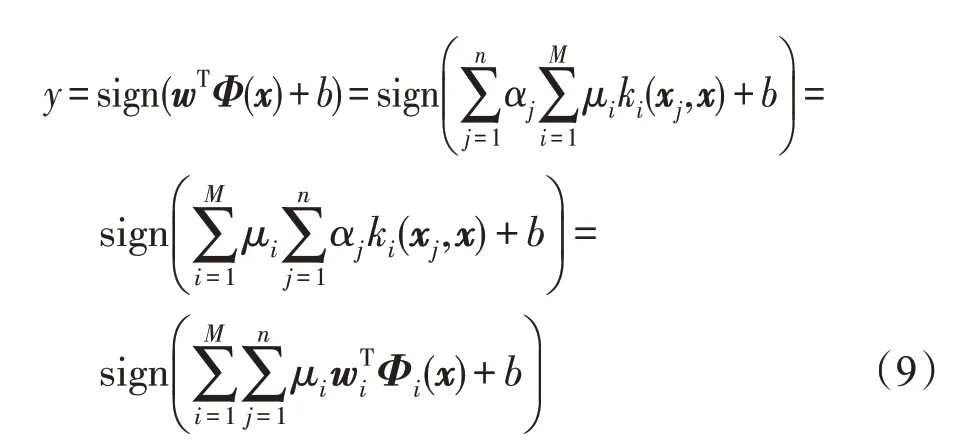
2.3 MK-LSSVM算法流程

算法1MK-LSSVM

输入：数据集D，阈值σ，基本核矩阵，算法参数λ。

输出：基本核矩阵权重和分类器参数{μ,w,b}。

步骤1核函数权重μi=1/M(i=1,2,…,M)。

步骤2初始化循环次数iter=1，循环：

步骤2.1计算合成核矩阵并由式（6）得{α,b}；

步骤2.2固定α，由式（8）更新μ；

步骤2.3判断是否有|1-fiter(μ,α)/fiter-1(μ,α)|≤σ，若是则跳至步骤3，否则跳至步骤2.1。

步骤3利用{μ,α}计算得分类器参数w。

3 基于多核学习的风格正则化最小二乘支持向量机

3.1 目标函数

为利用不同核函数对于数据映射的不同特性来表达样本之间物理相似性，同时挖掘数据集中样本包含的风格信息，将数据集内具有相同风格的样本划为一组，使用风格转换矩阵表示每组内样本包含的风格信息，并利用风格转换矩阵对样本的风格进行转换以使其接近标准风格，利用风格变换之后的样本对合成核矩阵进行更新，此时得到的核矩阵中的每个元素由经过了风格转换后的样本映射而成，并使用更新后的核矩阵对分类器参数进行学习。为将对样本进行风格转换的程度控制在适当范围内，在目标函数中利用正则化方法对风格转换矩阵进行限制。根据上述思路，训练分类器参数和风格转换矩阵的过程不仅保留了多核学习方法的优点，同时充分挖掘并利用了数据集中包含的风格信息。由以上思想，提出MK-SRLSSVM的模型定义：

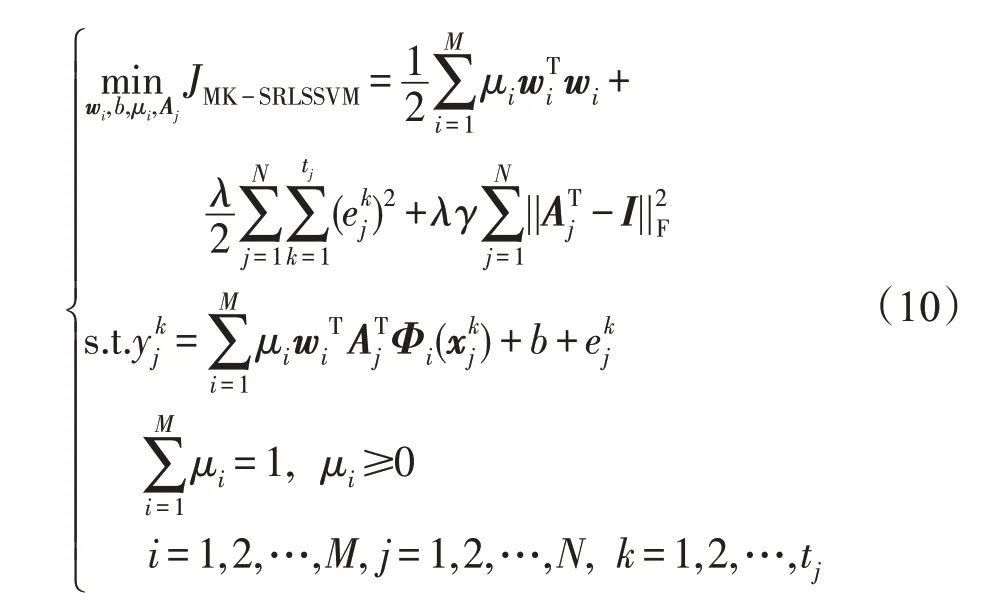
JMK-SRLSSVM中的前两个子式为标准MK-LSSVM表达式，第三个子式为一个使用Frobenius范数的惩罚项，用于控制风格转化矩阵对样本的风格变换程度，其中参数γ∈R且γ＞0。显然，当γ越大时，经过风格转换之后的样本与其原始风格偏离越小，否则越大；特别的当设置γ→+∞时，则有

3.2 目标函数优化

算法目标是令JMK-SRLSSVM值最小化，直接对目标函数进行优化较为困难，可以使用交替优化方法得到一个足够可用的局部最优解。当分别给定Aj和{wi,b,μi}时，则目标函数分别为关于{wi,b,μi}和Aj的优化问题，重复以上两个过程，直到收敛或超过最大迭代次数。具体步骤为：

（1）当优化{wi,b,μi}时：固定Aj(j=1,2,…,N)，则式（10）的优化问题转化为：

（2）当优化Aj(j=1,2,…,N)时：固定{μi,wi,b}时，则式（10）的优化问题转化为：

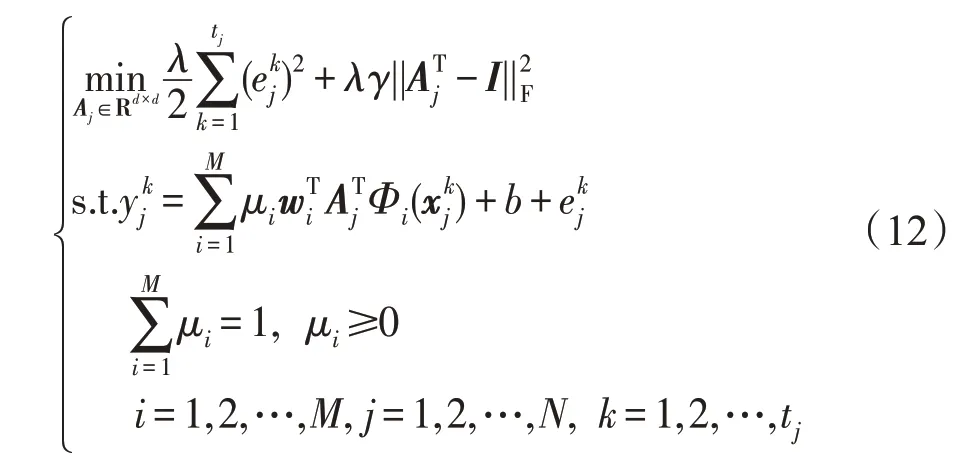
上式是关于Aj的线性约束的二次规划问题，可以转化为N个分别关于每个Aj的独立问题进行求解。此时合成核矩阵与分类器参数已经固定，与原始LSSVM相似，对式（12）引入拉格朗日乘子后可得其对偶形式：

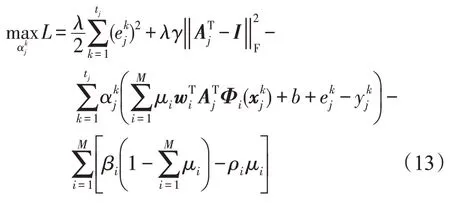
令∂L/∂Aj=0可得：

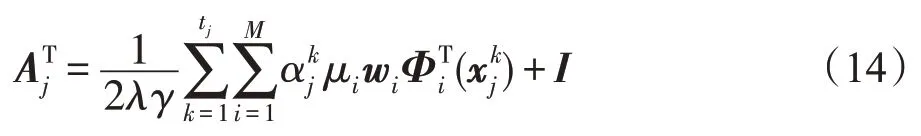
通过交替优化的过程可知，在训练分类器参数的过程中，将经风格转换矩阵转换后的样本作为训练数据。在第一轮迭代中，风格转换矩阵被初始化为单位矩阵，此时被风格转换之后的样本与原始样本相同，并没有产生风格变换，因此MK-SRLSSVM首轮训练得到的分类器参数与原始MK-LSSVM得到的分类器参数相同。在之后的迭代过程中，由于风格转换矩阵的优化，各风格组中的样本经过风格转换矩阵的变换，逐渐逼近标准风格，此时训练出的分类器参数充分考虑了样本整体包含的风格信息。同时，从式（14）可得求解风格转换矩阵的过程不仅利用了训练得出的样本的物理特性，且有效利用了数据中的风格信息，此时训练出的风格转换矩阵包含了各风格组中的风格信息。根据以上分析，训练分类器参数和风格转换矩阵的过程都充分利用了样本包含的风格信息，且两个过程相互促进。

3.3 样本风格转换

由于样本被映射到高维空间之后的维度可能是无穷的，导致无法直接得到经过风格转换后的样本值，此时可以借助核方法，对合成核矩阵中的每个元素进行更新，得到风格转换后的合成核矩阵。

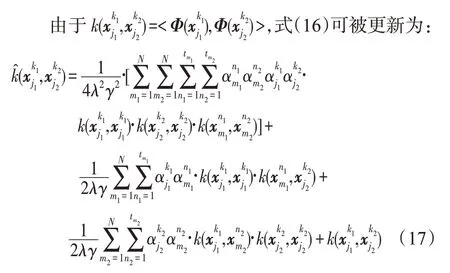
3.4 算法框架

MK-SRLSSVM算法的框架如图2所示。先使用多个预定义的基本核函数训练出权重系数μ，并生成合成核矩阵，使用合成核矩阵训练得到分类器参数{w,b}与风格转换矩阵{Aj}(j=1,2,…,N)，将未知样本进行风格转换之后使用分类器得到最终的预测结果。

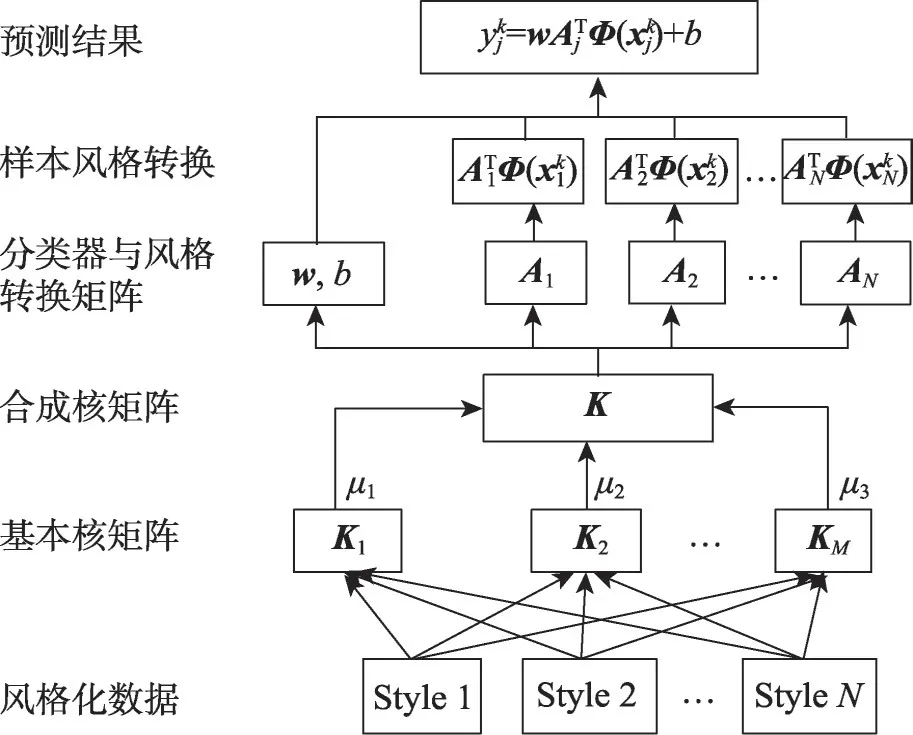
Fig.2 Algorithm framework图2 算法框架

3.5 算法训练步骤

算法2MK-SRLSSVM

输入：训练数据集D，最大迭代次数maxIter，收敛阈值ε，算法参数λ和γ。

输出：权重μi、分类器参数{w,b}、风格转换矩阵{Aj}。

步骤1初始化风格转换矩阵Aj=I(j=1,2,…,N)，核函数权重μi=1/M(i=1,2,…,M)。

步骤2初始化循环次数iter=1。

步骤3循环：

步骤3.1计算目标函数值Viter；

步骤3.2由式（11）更新μi和{w,b}；

步骤3.3由式（14）更新Aj并由式（17）更新合成核矩阵；

步骤3.4计算目标函数值Viter+1并判断是否达到收敛条件或超过最大迭代次数，若是则停止循环；否则令iter=iter+1，循环继续。

3.6 算法训练过程的时间复杂度

MK-SRLSSVM使用交替优化方法对问题进行求解，可以分为两个步骤。第一步优化核矩阵权重系数和分类器参数的步骤又可以分为两个子过程，分别为求解核权重的SILP问题和求解分类器参数的线性规划问题，同时更新合成核矩阵，二者的时间复杂度分别为O(M2n3)和O(n)，由于M≥1，故这一步总的时间复杂度可视为O(M2n3)。第二步为优化风格标准化矩阵的过程，这一步的时间复杂度为O(N2n2)。因此算法训练过程总的时间复杂度为O(iter·(M2n3+N2n2))，其中M为预定义的基本核矩阵的个数，n为样本总数，N为数据集中的风格数量，iter为算法迭代次数。

相比典型的多核支持向量机（multiple kernel support vector machine，MKL-SVM）算法，MK-SRLSSVM在训练过程中虽然用风格转换矩阵对样本进行了风格正则化处理，但多核支持向量机类算法在求解基本核函数权重系数的过程中需要调用原始SVM进行求解，而本文算法则使用原始LSSVM进行求解，由于SVM的训练过程本质上是在求解二次规划问题，而LSSVM的训练过程的本质为线性规划问题的求解，故MK-SRLSSVM在此步骤的计算复杂度远小于典型MKL-SVM算法。本文算法通过求解SILP问题优化权重系数，优于通过求解SDP（semi-definite programming）问题或QCQP（quadratical constraint quadratic programming）等问题优化权重系数的支持向量机类算法，与使用SILP等问题求解权重系数的多核支持向量机算法相当。故MK-SRLSSVM具有与典型支持向量机类算法相当的复杂度。

3.7 样本预测规则

为利用训练得到的权重和分类器参数{μi,w,b}以及风格转换矩阵Aj(j=1,2,…,N)，在MK-LSSVM的基础上定义了两种新的预测规则。由于在现实应用中，样本的风格可能已在训练过程中出现过，也可能未在训练过程中出现，因此在传统的预测方法之上增加了两条新的预测规则规则2和规则3分别处理这两种情况。

规则1传统预测方法

传统预测方法仅使用权重μi和分类器参数w和b对测试集中的样本进行预测，得到对应的标签

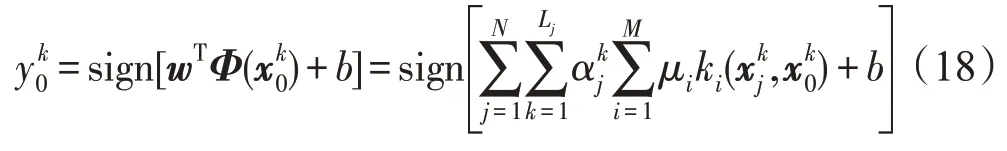
规则2测试样本风格已知

若测试样本的风格已在训练集中存在，则可以直接利用训练过程中学习得到的对应的风格转换矩阵对样本进行风格转换处理，使样本接近标准风格。然后对已处理的样本使用传统预测规则得到预测标签，即:

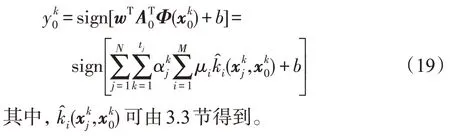
规则3测试样本风格未知

若样本组X0的风格不存在于训练集中，为有效利用训练所得的风格信息，使用直推式学习的思想，将同风格的样本组中包含的信息视为新的风格，在预测过程中使用训练集得到的分类器参数对样本标签进行初步预测，并在迭代过程中逐步修正分类器参数，同时优化新的风格转换矩阵。使用最终得到的优化后的新分类器参数和新风格转换矩阵对样本组标签进行最终预测。详细步骤如下：

步骤1使用预测规则1得到测试集X0的临时标签

步骤2将样本组X0及其临时标签Ytemp与训练数据集合并后进行训练，得到新的权重、分类器参数及风格转换矩阵

步骤3使用对测试集X0进行预测，得到正式的预测标签

由于现实场景中的大多数据均隐含或明显地包含一定的风格特征，而MK-SRLSSVM中增加的新预测方法考虑到了风格已知和风格未知的情况。直接使用与预测样本对应的风格信息对已知风格的样本进行预测；利用直推式方法对未知风格的样本进行预测，均有效地利用了训练出的风格信息，因此算法有较好的普适性。

3.8 算法性能特点分析

与传统支持向量机类算法仅根据原始数据的物理分布寻找最优分类超平面不同，MK-SRLSSVM算法不仅考虑了数据中包含的物理特征，同时挖掘了数据的风格特征。本文算法利用整体训练样本优化分类器参数的同时，对具有不同风格的数据组分别进行处理。借助于多核学习对数据映射的优势，本文算法可以对包含较为复杂风格的数据进行表示和处理，并在训练和测试方法中都充分利用了训练出的风格信息对原始样本进行风格正则化处理，使经风格转换后的数据分布更易于划分。较传统支持向量机及多核支持向量机类算法，MK-SRLSSVM可对风格化数据中包含的信息更加充分地利用以提高分类性能。

4 实验

4.1 实验数据和参数设置

为检验本文算法的分类效果，在4个风格化数据集中进行了多个实验，分别为：在来自剑桥大学（http://www-prima.inrialpes.fr/Pointing04/data-face.html）的人脸（Face Pointing）数据集中进行人脸分类实验；在来自UCI数据库（http://archive.ics.uci.edu/ml/index.php）的语音（Parkinson Speech）数据集中进行语音分类实验；在来自CASIA（http://www.nlpr.ia.ac.cn）的英文手写字母（English Handwriting）数据集中进行字母分类实验；在来自波恩大学（http://www.meb.uni-bonn.de/epileptologie/science/physik/eegdata.html）的癫痫脑信号（Epileptic EEG）数据集中进行EEG信号识别实验。

为了检测算法相对于多核学习算法的效果，对于所有数据集，选取8个包括新近以及经典的多核学习SVM算法进行比较，分别为GMKL（more generality MKL）[22]、非线性组合算法NLMKL（non-linear MKL）[23]、LMKL（localized MKL）[24]、RBMKL（rule-based MKL）[25]、GLMKL（group Lasso MKL）[26]、CABMKL（centered-alignment-based MKL）[27]、simpleMKL[28]以及新近的easyMKL[29]。另对于Epileptic EEG数据集，增加了两种常用于EEG检测的算法进行对比，分别是朴素贝叶斯算法（naive Bayes，NB）和决策树算法（decision tree，DT）。

对所有多核算法设置3种基本核函数，具体为：1个线性核函数k(x,z)=xTz，11个核带宽分别为σ={e-5,e-4,…,e5}的高斯核函数k(x,z)=exp(-||x-z||2/2σ2)，3个次数分别为d={1,2,3}的多项式核函数k(x,z)=(xTz+r)d，其中r=1。

在运行算法之前，需要对参数进行设置，所有算法的参数设置方法如下：先参考对应文献中推荐的参数设置，为选取最优参数，采用网格寻优策略在推荐值附近进行寻优。为保证对比公平性，对MKSRLSSVM的正则化参数λ和对比算法的正则化参数C设置相同的寻优范围均为{e-5,e-4,…,e5}，MKSRLSSVM中另一个参数γ的寻优范围为{e-5,e-4,…,e5}，easyMKL算法参数λe的寻优范围为{0.1,0.2,…,1.0}。所有多核学习算法的收敛阈值均设置为0.01，最大迭代次数设置为200。对于需要设置核组合规则的算法均采用默认值，具体为：RBMKL为平均组合，CABMKL为线性组合，LMKL为softmax。GMKL和NLMKL均取默认的L1范数。所有实验均在选取样本的全部特征的情况下进行。

由于大多数多核学习算法聚焦于二分类问题，对于多分类数据集，本文选取广泛使用的“一对一”（one vs.one，OvO）策略将多分类任务分解为多个二分类任务进行实验。

所有实验进行之前对数据进行两项预处理，分别为对原始数据的线性归一化处理和对基本核矩阵进行的标准化处理。线性归一化方法为：

核矩阵标准化方法为：

所有实验均在Matlab平台下进行，详细实验环境为：处理器CoreTMi5，2.80 GHz，内存12 GB，硬盘500 GB，操作系统为Windows 10专业版，Matlab版本为R2016b。

4.2 实验结果和分析

4.2.1 Face Pointing人脸数据集

Face Pointing数据集采集了不同姿态下的人脸图像，本小节选取垂直角度为0的图像进行实验。数据集中共有15个参与者的人脸数据，对每个人在水平角度下从-90°到90°每间隔15°采集一张图片，即包括每个人的各13张不同角度姿态的照片，因此实验数据集中总共包括195张人脸图像。

为体现出数据集中样本的风格差异，将部分代表性样本提取在图3中，图中共有10人，每人有3种姿态，每种姿态被视为一种风格，即每行的样本拥有同一种风格，图中共有3种风格的10类样本。

Fig.3 Part of face samples图3 部分人脸样本示例

实验中首先将每张图片缩放至36×48像素，再经过主成分分析[30]（principal component analysis，PCA）技术保留95%的信息后，将维度降到67维。选取每个人前7个姿态共105个样本作为训练数据，后6个姿态共90个样本作为测试数据。由于测试数据的风格相对于训练数据是未知的，因此使用规则3进行预测，实验结果如表1所示。

Table 1 Experimental results of Face Pointing dataset表1 Face Pointing数据集实验结果

从表1的实验结果中可以得出，在对比算法中NLMKL、RBMKL以及新近的easyMKL取得了精确度为0.893 3的良好效果，较其他多核学习算法在本数据集中的效果较好。而本文算法MK-SRLSSVM在与多核学习SVM算法的比较中取得了最好的分类效果，这是由于算法不仅利用了各基本核函数组成的合成核的映射优势学习得到分类器参数，而且挖掘了不同姿态的图像中包含的风格信息，并在对未知样本的预测过程中使用了学习得到的风格信息，相比只利用了数据集中的样本物理相似性信息的算法，MK-SRLSSVM有效提高了分类的效果。

4.2.2 Parkinson Speech语音数据集

本小节实验的语音数据集Parkinson Speech中包含了由帕金森患者和健康者提供的两类语音数据。其中训练集包含了来自于40个参与者的共1 040条语音数据，包括字母、数字、单词和短句；测试集中的数据全部来自帕金森患者，其中有168个元音样本，每个样本有28个维度，出自每个语音提供者的样本被视为具有同一种风格，实验结果如表2所示。

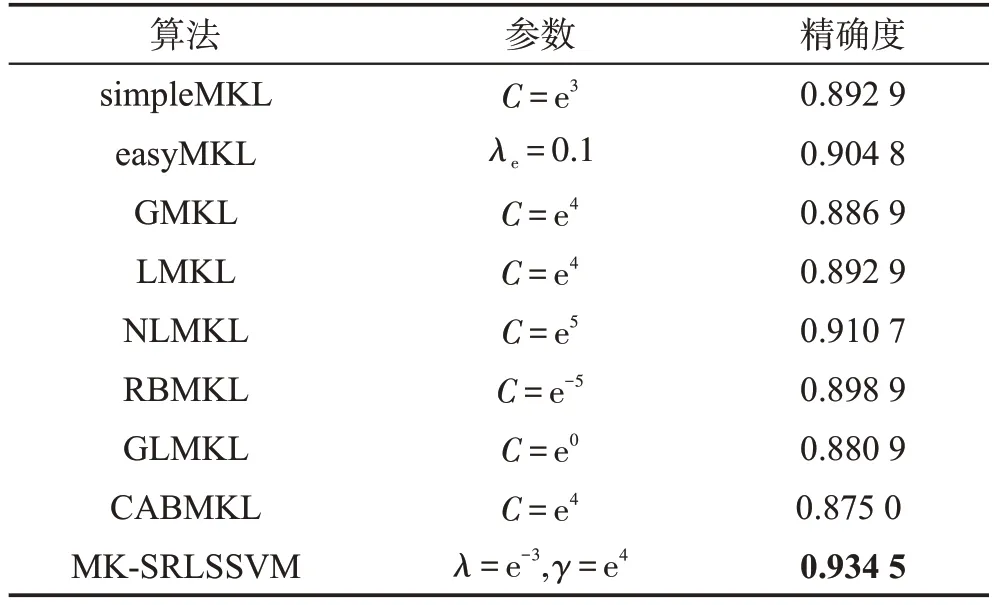
Table 2 Experimental results of Parkinson Speech dataset表2 Parkinson Speech数据集实验结果

根据表2的实验结果可得，在所有对比算法中NLMKL取得了较好的效果，而CABMKL相对较差，体现出多核学习算法中不同的核权重系数优化算法在性能上的差别。本文算法MK-SRLSSVM在所有算法中取得最好的分类效果，可见算法有效利用了各核函数在样本映射方法中对于样本物理相似性关系的不同表示的特点，而且挖掘了患者和健康人的语音样本中包含的不同的风格特征，分类效果的提高体现出本文算法对于语音数据中的风格信息进行挖掘利用的有效性。

4.2.3 English Handwriting手写英文字母数据集

本实验中English Handwriting数据集中的样本出自不同书写者，每个样本包含有笔迹、笔尖朝向、笔触压力等信息。由于每个书写者有着不同的书写习惯，这些书写习惯均体现在样本数据中，实验中来自每个书写者的样本被视为具有同一种风格。由于数据集中不同书写者的样本采集自不同的时间段（TIME），而书写者的时间段信息为无关因素，因此在本实验中不选取此属性。

为体现出数据集中包含的不同风格，提取了如图4所示的部分书写者的笔迹，图中包括3个书写人的手写样本，从中可以看出不同书写者具有不同的书写风格。

Fig.4 Examples of English Handwriting dataset图4 部分手写英文字体数据集示例

本小节选取数据集中前5个（no.1～5）书写者的各前1 000个样本点共20个类别的数据进行实验，其中前80%为训练数据，后20%为测试数据。即数据集中共有5 000个样本，其中训练集的样本数量为4 000，测试集的样本数量为1 000，共20个类别，样本维度为6。

从表3的实验结果中可以得出，本文算法相对于传统多核学习SVM算法的有效性。在对比算法中NLMKL和GLMKL取得了较好的效果，但相对于其他对比算法的优势较小，在本小节的实验中表现出相似的性能。而本文的MK-SRLSSVM算法则有效地挖掘了手写字母样本中的包括笔迹以及笔尖朝向等风格信息，并且在预测方法中有效利用预测规则对经过风格转换后的样本进行预测。而传统的多核学习方法虽然将多个核函数进行了结合，有效利用了样本之间的物理相似性，但是由于没有考虑到样本风格特征，因此较本文算法在分类精确度上有所差距。

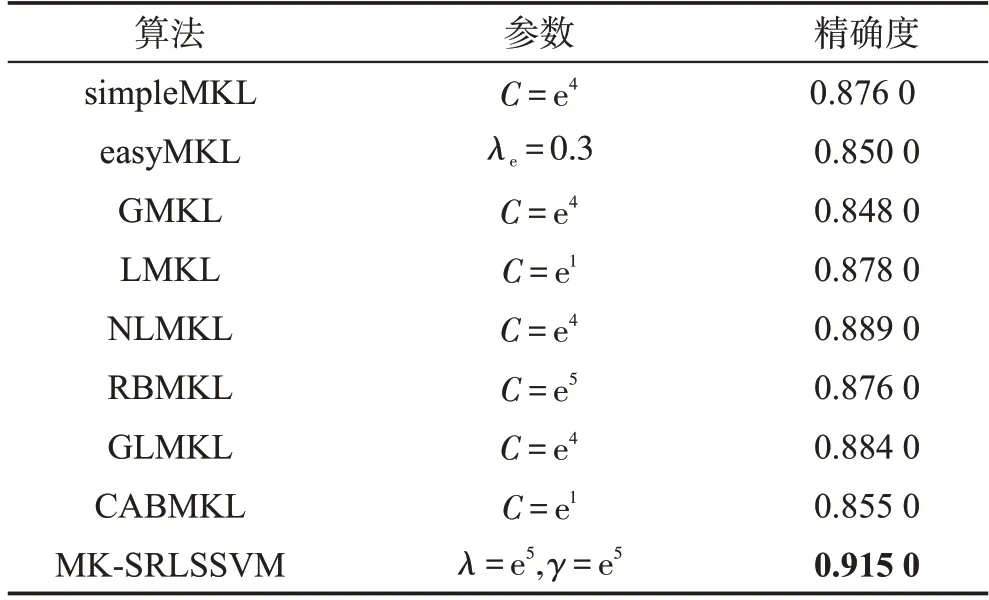
Table 3 Experimental results of English Handwriting dataset表3 English Handwriting数据集实验结果

4.2.4 Epileptic EEG数据集

本小节中的EEG数据集由5组采集自2类人群的样本组成，详细信息如表4所示，从每组中随机抽取的样本如图5所示。从图5中可以看出，来自不同组别的样本的波动性具有很大差别，例如A组中的患者和E组中的健康者的信号波动性差异明显；同为患者的C、E两组在不同情况下的信号波动性也相差较大。

Table 4 Description of Epileptic EEG dataset表4 Epileptic EEG数据集描述

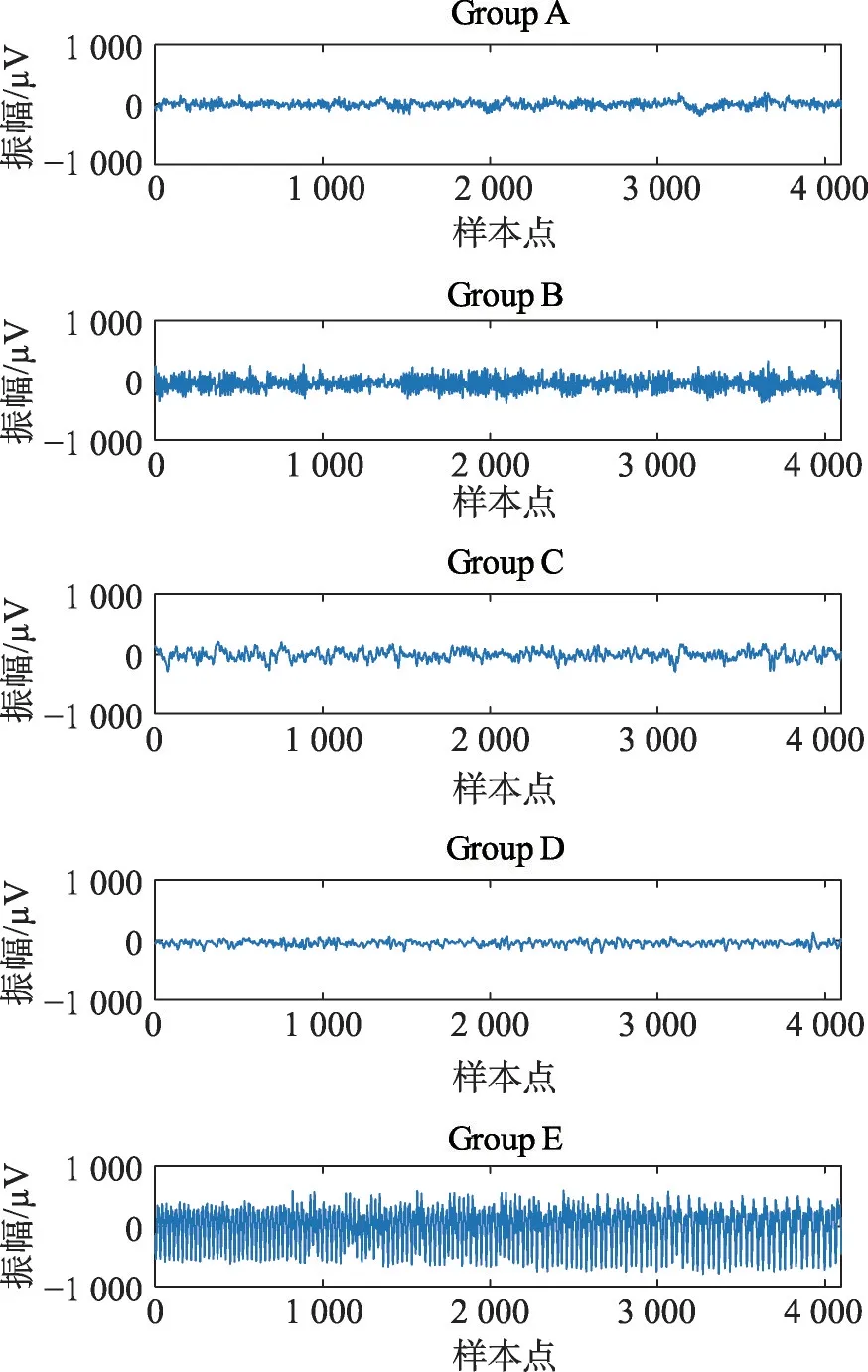
Fig.5 Raw EEG signal图5 原始EEG信号

研究[31]表明，预先对原始EEG数据进行特征提取可以有效提高分类性能，本文使用核主函数分析技术（kernel principal component analysis，KPCA）[4]对原始数据进行特征提取工作，提取后的样本维度为70，随机选取提取后的样本如图6所示。

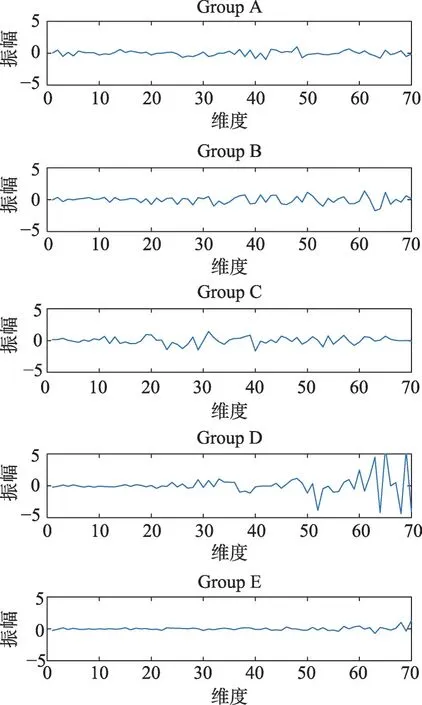
Fig.6 Extracted featured EEG signal图6 抽取的特征EEG信号

本小节使用降维后的数据进行实验，由上述可知数据集中样本数为500，类别数为2，样本维度为70，来自于同一组的样本被视为具有相同的风格。

为验证本文算法的有效性，对不同组别的数据进行选择以构成两种类型的数据集。第一类数据为测试集中包含的所有风格同时存在于训练集中；第二类数据为测试集存在训练集中所没有的风格，构造数据集的详细信息如表5所示。

数据集DS.1和DS.2为第一类数据，DS.3和DS.4为第二类数据，所有数据均为随机选取，并在同一组参数下进行10次实验，对结果取均值。对于两类数据结合使用规则2和规则3进行预测，实验结果及所有算法的参数如表6所示，同时在图7中绘出各算法在两类数据集中分类精确度的波动性。

Table 5 Detail of experimental datasets表5 实验数据集的详细信息

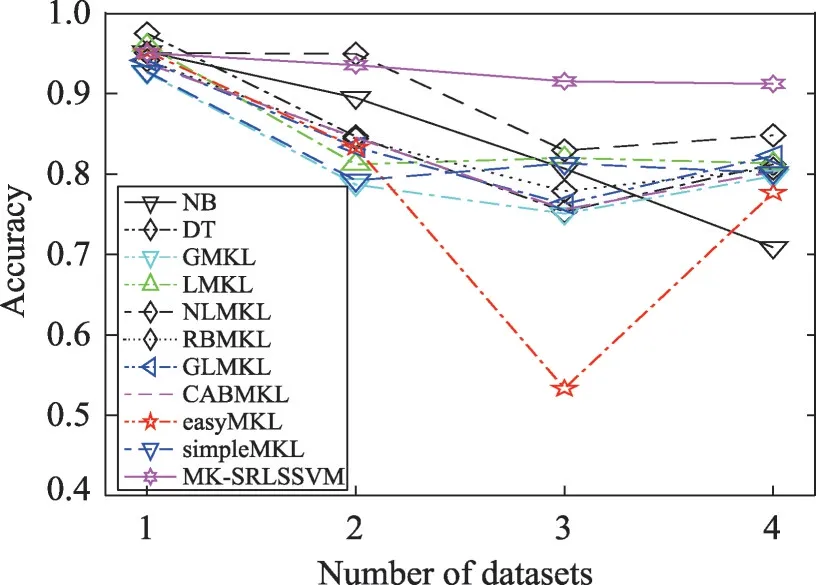
Fig.7 Accuracy volatility of EEG datasets图7 EEG数据集精确度波动

从表6的实验结果可以得出，在数据集DS.1中决策树算法取得最好的波动信号识别效果，在数据集DS.2中NLMKL算法有着最好的分类精度，领先于包括本文算法在内的其他所有的算法。而本文算法在前两个数据集中取得的效果虽然不如DT和NLMKL，但是相差较小。

从图7可以得出，在第二类数据集DS.3和DS.4中，当测试集中的样本风格未在训练集中出现时，对比算法中无论是多核学习算法还是常用于EEG信号识别的两种非多核学习算法的识别精确度相对于在第一类数据中的分类效果都有较大的降低，而MKSRLSSVM算法则保持了较高的分类精确度，在两类数据中的分类精度波动较小。通过以上结果可以看出本文算法对于各组样本中包含的不同波动特征的挖掘和利用对EEG信号识别精确度提高的有效性和稳定性。

4.2.5 参数敏感性分析

为进一步了解参数取值对于本文算法性能的影响，以在Epileptic EEG数据集中进行的4个实验为例，研究正则化参数λ和风格转换矩阵惩罚参数γ对算法性能的影响，如图8所示。

从图8中可得，当固定参数γ、λ取不同值时，算法的精确度在0.55～1.00之间波动，波动范围较大。在数据集DS.1和DS.2中算法的精确度随λ的增加而增加，而对于数据集DS.3和DS.4，算法的精确度在λ＜1时呈现递增的趋势，但是在之后逐渐降低。当固定参数λ,γ取不同值时，本文算法取得的精确度在0.75～0.95之间且随γ的增大而降低，波动幅度较小。可见相对于γ，λ的取值对于本文算法性能的影响较大，需要利用交叉验证结合网格搜索对其进行寻优。

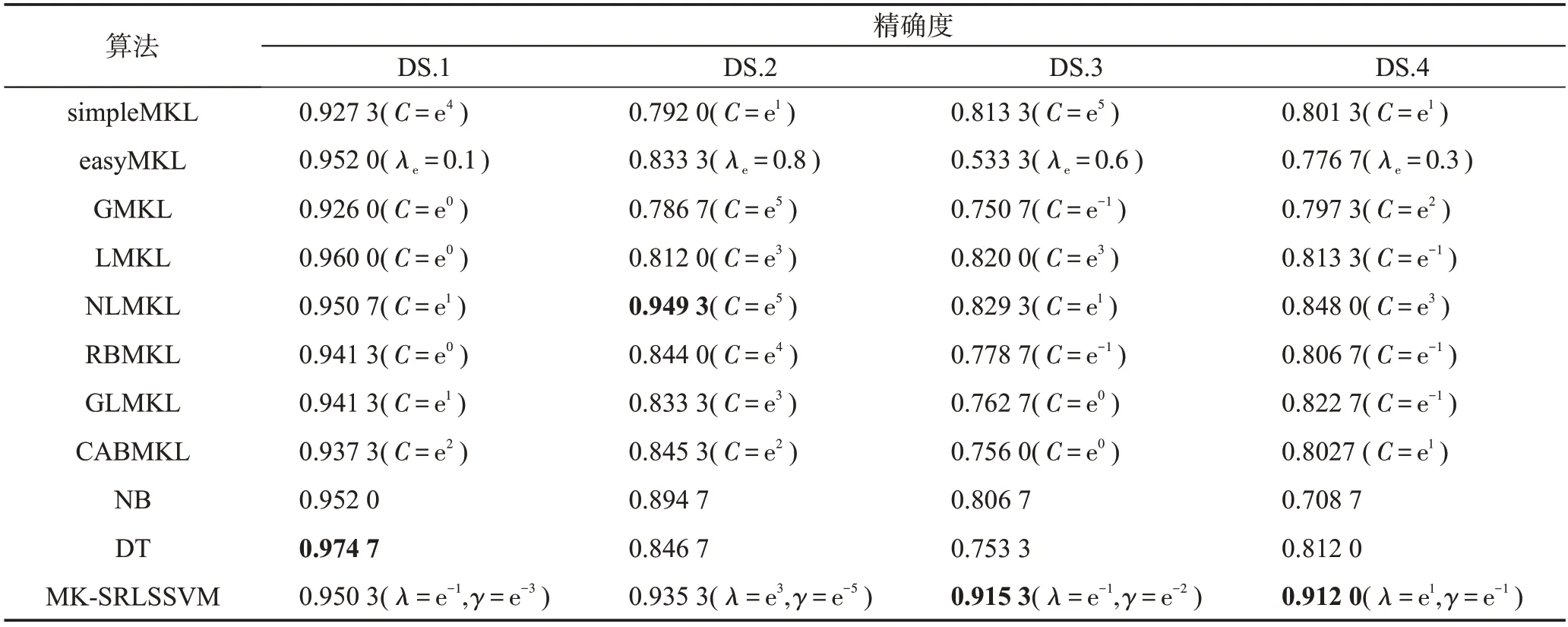
Table 6 Experimental results of Epileptic EEG dataset表6 Epileptic EEG数据集实验结果

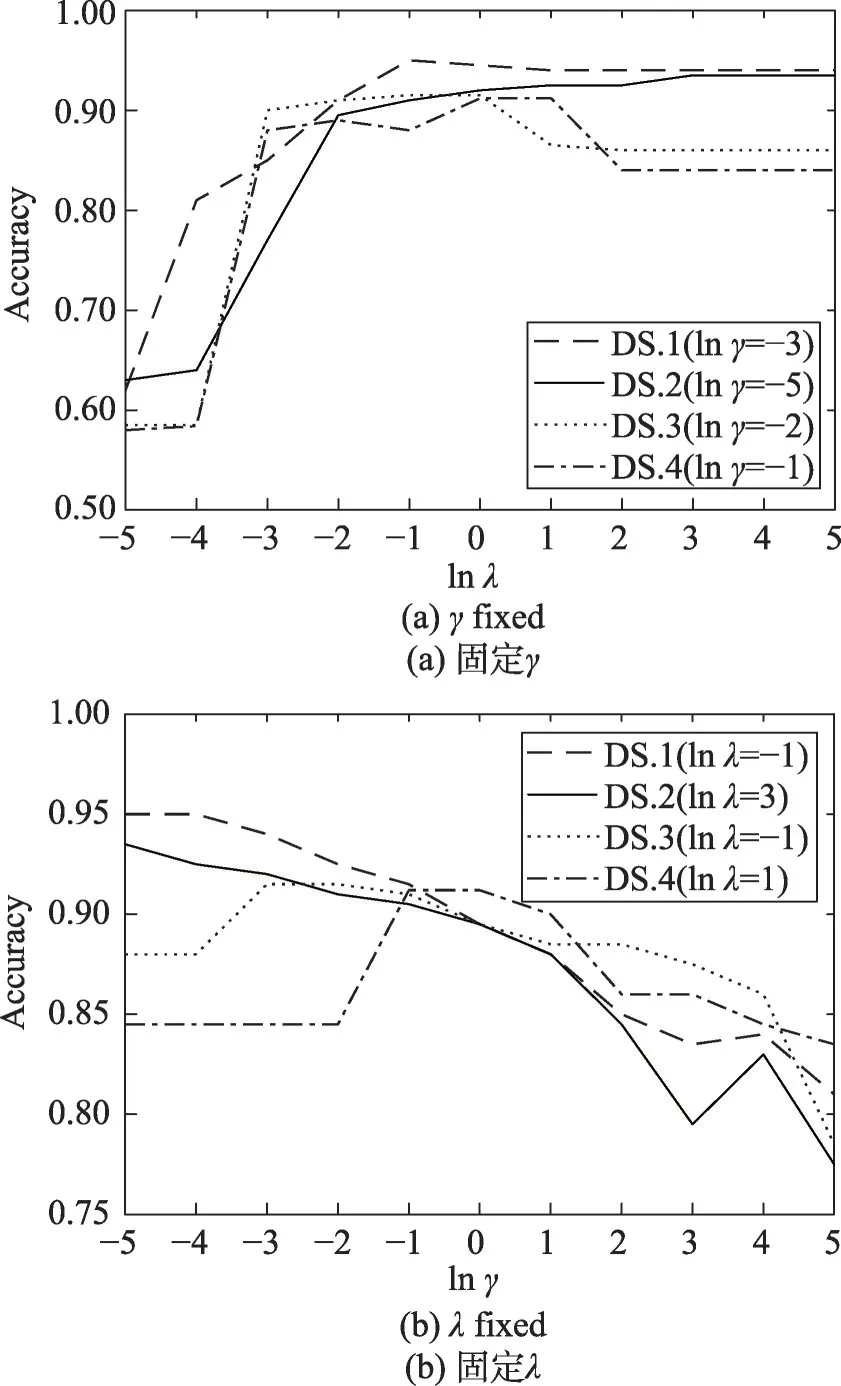
Fig.8 Sensitivity analysis of parameters图8 参数敏感性分析

5 结束语

为利用样本中包含的风格信息，本文提出基于多核学习的风格正则化最小二乘支持向量机（MKSRLSSVM）。该算法在利用了多核学习对于样本之间物理相似性表达的优势之外，同时挖掘并利用了样本包含的风格信息以提升算法的分类精确度。MK-SRLSSVM将样本包含的风格信息考虑进目标函数中，使用风格转换矩阵对样本进行标准化处理，并利用正则化方法对风格转换的程度进行限制，在训练过程中同时优化分类器参数和风格转换矩阵。并在传统的预测方法之上添加了可以利用训练出的风格信息的新预测规则。通过风格化数据集中的实验表明了算法的有效性和一定的实用性。