Theoretical prediction of radiation-enhanced diffusion behavior in nickel under self-ion irradiation

Xiao-Ya Chen· A-Li Wen · Cui-Lan Ren,3· Cheng-Bin Wang,3·Wei Zhang,3 · He-Fei Huang· Zhi-Wen Chen · Ping Huai,4,5

Abstract The enhanced diffusion in materials under irradiation plays an important role in the long-term microstructural evolution. In this work, the self-ion irradiation in nickel was used as a model system to study the effect of radiation-enhanced diffusion on the implanted ion profiles. Initially, the depth profiles of vacancies and implanted ions for nickel self-ion irradiation with ion energies up to 15 MeV were computed by the high-efficiency Monte Carlo code IM3D(Irradiation of Materials in 3D). The results are in good agreement with those predicted by SRIM (Stopping and Range of Ions in Matter).Then,diffusion coefficients as functions of temperature and damage rate were obtained, and the depth-dependent diffusion coefficients at various temperatures and damage rates were also illustrated. For this purpose, we used a temperature-dependent effective sink concentration for nickel, which was estimated from the available experimental investigations on the damage structures of irradiated nickel.At length,case studies on the time evolution of implanted ion profiles under the condition of nickel selfirradiation were performed and discussed based on Fick’s second law.The results help to understand the fundamental diffusion properties in ion irradiation, especially under higher-dose irradiation.

Keywords Self-ion irradiation in nickel ·Implanted ions ·Radiation-enhanced diffusion · Monte Carlo simulation

1 Introduction

Heavy ion irradiation with ～MeV energy has been widely used to understand the fundamental microstructural evolution in materials under irradiation[1].It is known that the enhanced atomic diffusion or mass transport under irradiation gives rise to the chemical and microstructural changes including point defect clustering, void formation,and even swelling, segregation, precipitation, etc. [1-4].These changes in structures or phases can significantly affect the physical properties and may further deteriorate the mechanical properties of materials. Thus, understanding the atomic diffusion in materials under irradiation is of critical importance for their application as structural materials.

Numerous experimental investigations and theoretical studies have been carried out to study the radiation-enhanced diffusion (RED) in materials under ion irradiation conditions up to now. Experimentally, the radiation-enhanced diffusion coefficients are measured in various systems; for example, the self-(63Ni isotope tracer) diffusion in natural nickel or nickel-based alloys [5-7], the nickel diffusion in copper [8], as well as the self-diffusion or dopant diffusion in semiconductor materials (the self-diffusion or dopant diffusion in natural silicon [9, 10], the phosphorus in germanium [11], the self-diffusion or boron diffusion in germanium [12], etc.). The main procedures are as follows [5, 7]: by considering a model of A layer sandwiched between B materials, or BABAB… layered materials (A is tracers of B or impurities), the broadening of depth profiles of A concentration in B materials (approximately Gaussian distribution) under ion irradiation can be measured in a wide temperature range. The enhanced diffusion coefficients can be calculated by comparing the depth profiles of A in B materials between two conditions: under thermal annealing and under irradiation conditions.

The experimental investigations showed that the depth profiles of A in B materials under irradiation conditions are generally broadened,and the broadening was enlarged with increasing radiation dose [13, 14]. Such an enhanced diffusion process can be understood theoretically by the solution of Fick’s second law. The enhanced diffusion in materials under irradiation can be attributed to the increased concentration of point defects (vacancies and interstitials), which is generally much higher than that under thermal equilibrium conditions. According to the defect reaction rate theory, the radiation-enhanced diffusion in steady state is determined by the competition between the production rate of freely migrating defects(FMDs) and the defect loss (to sinks or via vacancy-interstitial recombination) [15]. Meanwhile, the total diffusion coefficients under ion irradiation are generally considered from three aspects [5, 16]: temperature-independent ballistic mixing, long-term diffusion under irradiation, and thermal-activated diffusion (details will be shown later). It is recognized that the RED coefficient is a temperature-and damage rate-dependent quantity,and also varies in different target materials.Therefore,we carefully considered possible items that may affect the RED in this work, to get a comprehensive understanding of the diffusion under ion irradiation: (a) Accurate estimation of the depth-dependent damage rate and percentage of FMDs.The depth profiles of primary radiation damages for ion irradiation can be estimated by the widely used Monte Carlo (MC) code SRIM (Stopping and Range of Ions in Matter) [17] or IM3D (Irradiation of Materials in 3D)codes [18]. It is recognized that the ‘‘Quick Kinchin-Pease’’ (QKP) method is widely used to estimate the damage dose in modern ion irradiation experiments.(b) Accurate estimation of the effective sink concentration or sink strength, a quantity that determines the absorption efficiency of defects. A constant effective sink concentration was generally used to estimate the diffusion coefficients. However, it is also a temperature-dependent quantity and needs further improvement. (c) Good selection of the material-related parameters for thermal-activated diffusion,as there are large variations in the reported data from the available previous studies.

In addition,understanding the time evolutions of atomic profiles under ion irradiation also has practical significance in fully understanding their long-term radiation effects.It is worth mentioning that for accelerator-based ion irradiation,the mass mainly flows along the ion projected range (1D flow, with respect to 3D diffusion under neutron irradiation), which arises from the forward scattering of ions as well as the surface sinks [3, 13]. Thus, it gives rise to an artificial effect during the long-term microstructural evolution. For example, the implanted ions can cause depthdependent compositional modifications and further enhance the amorphization processes and suppress void swelling when ions come to rest [2, 3]. For example, the precipitation in irradiated Fe-15 at%.Cr alloy under Fe ion irradiation exhibits a depth-dependent phenomenon that the as-implanted Fe ions reduce the α′precipitation [4]. As a consequence of the artifacts from strong surface sinks and injected interstitials, the near-surface depletion region and peak implanted regions are generally avoided when examine their irradiation effect. Recently, Zinkle et al.[19] investigated that the safe midrange-depth region shrinks with increasing radiation dose or temperature and even disappears at a higher dose and elevated temperature.Doyle et al.[14,20]systematically studied the diffusion of as-implanted ion profiles for the systems of self-ion irradiation in iron and nickel using Fick’s second law. Higher energies (＞6-8 MeV, depending on the target materials)are recommended to achieve safe regions for swelling analysis under doses ＞100 dpa. Thus, the time evolutions on the depth profiles of implanted ions are of practical significance in understanding the diffusion-related phenomenon under irradiation.

In this work, the self-ion irradiation in nickel was used as a model system to study the effect of RED on the implanted ion profiles due to the increased interest in the potential application of nickel-based alloys, which have been accepted as one of the promising candidates for the structural materials in high-dose Gen IV nuclear reactors,especially for the molten salt reactors (MSRs) [21-23].First, the depth profiles of primary radiation damages including vacancies and implanted ions were predicted by using the high-efficiency MC code IM3D.The results were compared with those predicted by SRIM as benchmark calculations. Second, the acquisition of key parameters used for diffusion coefficients under nickel self-ion diffusion were discussed, and temperature- and dose rate-dependent diffusion coefficients were obtained accordingly.In particular,an improved temperature-dependent effective sink concentration for nickel was estimated from the available experimental results on the damage structures of irradiated nickel. Third, broadening of the spatial distribution of implanted ions along the ion bombarding direction for nickel under self-ion irradiation was studied and discussed.

2 Theoretical details

2.1 Details for IM3D calculations

Primary radiation damages for self-ion irradiation in nickel were predicted by using the recently developed high-efficiency IM3D code with the ‘‘QKP’’ method [18].IM3D is an open-source parallel 3D MC code with binary collision approximations(BCAs)for rapidly simulating the energetic ion transportation and defect production in materials.Based on fast indexing of scattering integrals and the SRIM stopping power database, IM3D can well reproduce SRIM results for bulk or layered materials and is ＞104times faster than SRIM. Thus, IM3D is a more suitable tool to realize the high-throughput calculations in energetic ion-target interaction systems.

As shown in the schematic graph in Fig. 1, the spatial distributions of primary radiation damages for self-ion irradiation in bulk nickel with incident ion energies up to 15 MeV and normal incidence were predicted. The displacement threshold energy of 40 eV for nickel was used during the calculation.For each calculation,106nickel ions were averaged to get convergent defect productions. The target was divided into a certain number of bins with each size of 30 × 30 × 30 nm3.The parameter settings for ions and targets during the calculations are summarized in Table S1 in the Supplementary Materials.

2.2 Radiation-enhanced diffusion coefficients

The theoretical framework of RED has been successfully developed from the rate theory of defect evolutions[5,13].The atomic diffusion in materials under irradiation mainly arises from the following three aspects [5, 16]:

where the first item Dmixon the right-hand side (RHS) is related to the atomic mixing [16, 24]. The atomic displacement cascades start immediately after the primary knock-on atom (PKA) event and propagate for approximately 10 picoseconds until all atoms ballistically come to rest. During the cascade, significant quantities of replacement and displacement of atoms, and recombination and agglomeration of defects happen. Such diffusion process dominates at low temperature and is a temperature-independent quantity, which can be described by the Einstein relation

where R is the nearest-neighbor distance, and η is on an order of 102-103from experimental measurements [25].K is the atomic displacement rate in dpa/s. The displacement rate is considered to be near a constant on the scale of micrometers (even centimeters) under neutron irradiation,while it is a depth-dependent quantity in accelerator-based ion irradiation.The displacement rate in ion irradiation can be estimated by SRIM/IM3D with the ‘‘QKP’’ model[17, 18].

The second item Dradon the RHS of Eq. (1)is related to the long-range transport of atoms. After irradiation, the concentrations of point defects including vacancies and interstitials are much higher than those at the thermal equilibrium condition. These point defects, which have high mobility at elevated temperature, show a long-distance diffusion character. Theoretically, all mobile point defects and defect clusters contribute to Drad:

where fnvand fniare the geometrical correlation factors for the corresponding defect clusters, and n is the size of the vacancy or interstitial clusters.In this work,only the single vacancies and interstitials are simply considered, and their

where rivis the radii of vacancy-interstitial recombination,rvsand risare annihilation radii for vacancy and interstitial respectively at sinks,and Ω=a30/4 is the atomic volume of the target materials. The equivalent effective sink concentration Csis assumed to characterize the defect sinks in materials [5]. Then, the sink strength [7] can be written as

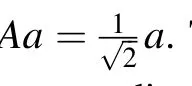
The parameters discussed above are listed in Table 1,in which the values from the available previous studies and used in this work are also collected.

The third item Dthon the RHS of Eq. (1)is related to the thermal diffusion, which can be expressed by a relation in the form of the Arrhenius equation.

where D0is the pre-factor for the diffusion coefficient,Q is the activation energy, and kBis the Boltzmann constant.

3 Results and discussion

3.1 Primary radiation damage calculations

As mentioned above, accurate estimations of the damage rates under ion irradiation are one of the key concerns in calculating the diffusion coefficients. In this subsection,the high-efficiency MC code IM3D was adopted to predict the depth profiles of primary radiation damages for self-ion irradiation in bulk nickel, as illustrated in Fig. 1. It is known that SRIM/TRIM is the most widely used tool for calculating the spatial distribution of primary radiation damages, including vacancies, interstitials, injected ions,etc., in energetic ion-material interactions. Therefore, we first performed benchmark calculations in the same ion irradiation systems.

The depth profiles of vacancies and implanted ions for self-ion irradiation in nickel calculated by IM3D are shown in Fig. 2a,b,respectively.Five independent examples with ion energies of 1, 3, 5, 10, 15 MeV and normal incidence are plotted and compared with the predictions from SRIM(see the dot points in black). Good agreements between IM3D-QKP and SRIM-QKP are found in predictions of the depth distributions on vacancies and implanted ions. With the increase of ion energy, the peaks of vacancy concentration (or dose rate) and implanted ion concentration (or implanted ion rate) move deeper correspondingly. Moreover, their peak concentrations gradually shrink with increasing ion energy.

The averaged ion projected ranges (Rps) with ion energies up to 15 MeV are also drawn to get a better comparison between IM3D and SRIM. As shown in Fig. 2c, the ion projected ranges predicted by IM3D (solid black line) are in good conformity with the results of ion stopping and range tables calculated by the SRIM code(red dash-dotted line), especially for the situations of ions with lower energies. The discrepancies between them (absolute errors) are evaluated by

With increasing ion energy, the projected ranges calculated by IM3D go slightly deeper when compared with those predicted by SRIM.The absolute errors are less than approximately 0.13 μm for all ion energies considered (up to 15 MeV)in this work,indicating a good correspondencebetween the calculations of IM3D and SRIM with the QKP method.

Table 1 Material parameters available from previous references and used in this work

The depth profiles of dose and atomic concentrations[32]for nickel self-irradiation with energy of 10 MeV with different radiation doses are plotted in Fig. 2d.The damage profiles were predicted by the IM3D-QKP method with various total ion fluencies in a range of 1014to 5 × 1017#/cm2, corresponding to the peak doses from ～0.1 to 500 dpa. The damage peaks appear at a depth of 2.38 μm,which is about 0.25 μm shallower than the peak position of injected ion concentration (2.63 μm). Such results are also in good agreement with those predicted by SRIM. The longitudinal straggling ranges for ions go deeper with increasing damage dose. For the damage dose considered here, the damaged region at levels exceeding 10-3dpa is found at a depth less than 3.10 μm for a peak damage dose of 0.1 dpa, whereas it increases to 3.33 μm for a peak damage dose of 500 dpa.

Generally,the concentration of implanted ions in nickel self-ion irradiation is approximately four orders of magnitude smaller than that of vacancies by a rough comparison between Fig. 2a,b.The implanted ions can be ignored at lower damage doses; for example, the peak concentration of implanted ions is only ～1.5 × 10-3% when the peak damage is ～0.1 dpa. In contrast, it reaches nearly 1.5%when the peak damage dose is up to ～100 dpa(with total ion fluencies of 1017#/cm2), which can no longer be readily ignored.

3.2 Radiation-enhanced self-diffusion in nickel

As discussed in Sect. 2.2, three main aspects contribute to the diffusion under irradiation: the long-range diffusion Drad, the cascade mixing Dmix, and the thermal-activated diffusion Dth.The former two items are related to the RED.Various parameters should be carefully considered to get relatively accurate RED behavior: (1) the depth-dependent damage rate under ion irradiation; (2) the effective sink concentration or sink strength for the target materials; and(3) the thermal-related diffusion parameters including the activation energy and the pre-factor.

The displacement rate for ion irradiation can be estimated from the primary radiation damage calculated by MC code SRIM/IM3D, as discussed in Sect. 3.1. The surface, dislocation, and grain boundaries in materials, as well as the radiation-induced voids, dislocation loops/networks etc., all behave as sinks for the point defects [1].Here, the effective sink concentration (Cs) in nickel is estimated from the contributions of dislocations and voids[33]:

where Λ is the dislocation density, Chis the atomic concentration of voids, rhis the void radius, and Z is the geometrical factor for defect loss at dislocations as shown in Table 1. This definition may provide a lower-bound estimation of the effective sink concentration in materials.The calculated Csas a function of temperature are displayed in Fig. 3a, in which the dislocations and void concentrations are mainly considered. To do this, the material parameters including the dislocation densities and void concentrations from experimental measurements via transmission electron microscopy (TEM) are collected and analyzed,as listed in Table S2[34-36].These data include the measurements from irradiated bulk nickel under selfion and neutron irradiations (see Note 2 in the Supplementary Materials) [34-36].

Figure 3a shows the tendency of effective sink concentrations, the pink dashed lines are obtained by numerical fitting on the nickel self-ion irradiation data shown in the figure. The blank dashed lines depict the Csfor lower and higher displacement rates. A general tendency can be found that Csincreases progressively when the dose rate increases.The Csexhibits relatively lower values at higher temperatures with 10-7order of magnitude, and it gradually increases and then decreases slightly when the temperature decreases. The peak Csshifts to the left (higher temperatures) and higher concentrations with gradually increasing dose rates, exhibiting a similar tendency to that of swelling properties as a function of temperature in structural materials. The Csshown in Fig. 3b exhibits an effect of defect saturation with increasing dose.In addition,we did further comparison of effective sink concentrations under different irradiation conditions, in which the influence of helium irradiation on Csis mainly discussed. The details are provided in Note 2 in the Supplementary Materials.

The third item is related to the thermal diffusivity of nickel self-diffusion, which can be written in Arrhenius form as shown in Eq. (10).Here,by reviewing the previous theoretical and experimental studies, the pre-exponential factors and activation energies(parameters in Eq. (10))for nickel self-diffusion are collected and listed in Table 2.The corresponding Arrhenius plots are shown in Fig. 4a.It can be seen that the thermal coefficients vary greatly among different methods. By analyzing these data, the experimental values from the work of Maier et al. were adopted to calculate the diffusion coefficients for nickel under ion irradiation [38].

Based on the above discussion,the diffusion coefficients of nickel under self-ion irradiation as a function of temperature and displacement rates are plotted in Fig. 4b.Here,displacement rates in a range of 10-4-10-2dpa/s are selected, which are commonly used in ion irradiation experiments on nickel-based alloys.Other parameters used for the prediction of the diffusion coefficients are listed in Table 1. In addition, a temperature-dependent Cswas carefully considered (see Fig. 3a). Moderate effective sink concentrations Csindicated by the dashed pink line wereassumed for the damage rate of 10-3dpa/s, while the scaled Csaccording to the general tendency of Csshown in Fig. 3a were used for other damage rates. The estimated diffusion coefficients are in good agreement with the experimental measurements of tracer diffusion in bulk nickel, as the circles and diamonds show (representing the diffusion under the equivalent dose rates of 1.2 × 10-4and 1.2 × 10-2dpa/s, respectively; corresponding data are provided in Table S3 in the Supplementary Materials) [5].It can be seen that the influence of radiation on atomic diffusions is promoted under higher damage rate.

Table 2 Diffusion pre-factors and activation energies for nickel selfdiffusion available in previous studies

As shown in Fig. 4b, the contributions from thermal diffusion (pink dash-dotted line), radiation-enhanced (red dotted line), and atomic mixing (blue dashed line) are also clearly shown. Let us take the damage rate of K = 10-3dpa/s as an example to illustrate the diffusion mechanisms.At very high temperature (＞1000 K), the thermal diffusion dominates due to the higher mobility of point defects.The effect of radiation on atomic diffusion gradually increases with decreasing temperature (from 1000 to 600 K). Previous studies showed that the diffusion coefficients in some parts of this temperature range exhibit a temperature-independent phenomenon due to the higher sink annihilation rate on defects [1, 5, 42]. However, by considering the temperature dependence of Cs, it can be speculated that diffusion mechanisms are related to both defect annihilation in sinks and defect recombination. In other words, defect recombination is also important due to the relatively lower Csat higher temperatures estimated from experimental investigations. At lower temperatures(＜650 K), the ballistic mixing diffusion Dmixis proportional to the damage rate, and it is estimated to be 1.1 × 10-21m2/s for K = 10-3dpa/s. The defect recombination is promoted due to the lower mobility of point defects, whereas the influence of defect sinks is less important. Besides, defect recombination also dominates for higher-dose-rate situations due to the higher concentration of defects.

The depth dependence of diffusion coefficients (Drad)for nickel under self-ion irradiation conditions was also estimated. A specific temperature range of 900-950 K is chosen, which is around the operating temperature of MSRs (650 °C, or 923 K) [21, 22]. We considered the ion irradiation with various energies (5, 10, and 15 MeV)under ion fluxes of 1012and 1013#/cm2/s, which correspond to peak damage rates of ～10-3and ～10-2dpa/s,respectively, due to the similarity of depth-dependent diffusion coefficients between different ion energies. The depth-dependent diffusion coefficients for 10 and 15 MeV are plotted in Note 3 in the Supplementary Materials. We took the 10 MeV nickel ion irradiation with peak damage rates of 10-3dpa/s (Fig. 5) as an example to illustrate the temperature and depth dependence on diffusion coefficients. The peak damage rate for 10 MeV nickel self-ion irradiation was estimated to be 0.9 × 10-3(rounding up to 1 × 10-3) dpa/s at a depth of ～2.4 μm. The peak Dradwas estimated to be ～0.6 × 10-19(blue dotted line)and ～0.9 × 10-19(pink dotted line) m2/s at 900 and 950 K, respectively, while the total diffusion coefficients D* were calculated to be ～0.7 × 10-19(bold blue line)and ～1.4 × 10-19(bold pink line) m2/s for the temperatures of 900 and 950 K, respectively. It can be seen that both Dradand Dthincrease with increasing temperature. In particular, the ratio of thermal-activated diffusion is significantly increased for total diffusion coefficients at 950 K.It also can be seen that the temperature-independent component Dmixhas little influence on the total diffusion coefficients D* at high temperatures. The calculated diffusion coefficients D* were also compared with the previously available experimental investigations on the nickel tracer diffusion under similar self-ion irradiation conditions, showing that they are of the same order of magnitude. According to Eq. (8), Dradis approximately proportional to the root value of damage rate(K0.5or K00.5).The diffusion coefficients are also in coincidence with the results of Doyle et al.’s calculations. They studied the diffusion coefficients of nickel under ion irradiation with a simplified model, in which the depth-dependent RED coefficients are proportional to(Ki/Kmax)E.The exponential scaling factor is in a range of 0.5-1.0, denoting the recombination-dominant and sink-dominant defect evolution mechanisms [14, 20]. However, when using a temperature-dependent effective sink concentration, it is shown that both sink annihilation and defect recombination are involved for the defect evolutions at the temperature of interest.

3.3 Radiation-enhanced diffusion of as-implanted ion profiles

The as-implanted ions in heavy ion irradiation exert a profound effect on the microstructural evolution of target materials.The typical artifact phenomenon is related to the depth-dependent precipitation in materials and the suppression of void swelling when the ions come to rest.Thus,a detailed investigation on the time evolution of the implanted ion profiles in heavy ion irradiation is of significant importance to understand the chemical change,and even the macroscopic properties such as void swelling. In this subsection, the diffusion of implanted ion profiles under irradiation is studied to identify their long-term evolution. Herein, the depth profiles of implanted ions(tracers implantion assumed)in nickel are used as a start to see the RED in nickel self-ion irradiation.The concepts for this method are in successful description of the evolution for depth-dependent atomic profiles under ion irradiation conditions by considering the RED and surface sputtering[13, 14, 43, 44]. Details are provided in Note 3 in the Supplementary Materials.

It is recognized that a higher diffusion coefficient can give rise to a larger broadening of the atomic profile under similar irradiation conditions.The diffusion coefficients are both temperature- and damage rate-dependent quantities.Thus,relatively higher total damages under fast irradiation(higher damage rates) were selected to see the influence of RED on the broadening of atomic profiles. As shown in Fig. 6a,we first studied the influence of damage rate on the broadening of atomic profiles under ion irradiation with ion energies of 5, 10, 15 MeV. Two damage rates with peak values of roughly 10-3and 10-2dpa/s, peak total damage of ～250 dpa and a temperature of 900 K were selected.The depth-dependent diffusion coefficients shown in Fig. S2 were adopted during the calculation. It shows that the total diffusion coefficients for ion energies of 5, 10,15 MeV at the peak damage position were all calculated to be roughly 2 × 10-19m2/s for the peak damage rate of ～10-2dpa/s(see Fig. 4b and Fig.S2).The irradiation time was estimated to be 7 h to get the total damage dose up to 250 dpa.Broadening of the atomic profiles was found for the ion energies of 5, 10, 15 MeV, and the peak concentrations were reduced by approximately 3-5% when compared with those that did not consider the RED effect.Meanwhile, for the situations under the damage rate of 10-3dpa/s, the total diffusion coefficients at 900 K were estimated to be approximately 0.7 × 10-19m2/s for ion energies of 5, 10, and 15 MeV. Significant broadening of the atomic profiles was found with peak concentrations reduced by approximately 10-13% during ～70 h irradiation (250 dpa), indicating the consequence of longterm irradiation.

Then, the time evolution(or dpa dependence) of atomic profiles for nickel self-ion irradiation with energies of 10-15 MeV was selected to avoid the surface effect on long-term irradiation, in which the depth-dependent diffusion coefficients shown in Fig. 5 and Fig.S2 were adopted.The evolutions of atomic profiles (regions for peak concentration) under irradiation with 10 and 15 MeV are shown in Fig. 6b and Fig. S3, respectively. As seen from the results of 10 MeV irradiation shown in Fig. 6b, significant broadening is obtained with the total damage reaching 500 dpa, and the peak concentration reduced to ～83% when compared with that the RED effect was not considered. Moreover, a much-simplified model in which we used a constant coefficient in the ion projected range was also considered for comparison. The broadened profiles are plotted in Fig. 6b(see the blue dotted lines).It can be seen that using a flat peak diffusion coefficient would not exert notable difference in broadening of the atomic profiles with the total dose considered in this work.

The two case studies show the time evolution of the depth-dependent atomic profiles. Significant broadening is found with increasing total damage (or dpa). It is recognized that atomic diffusion in ion irradiation is generally along the ion-bombarding direction(1D diffusion).Thus,a broad beam situation is assumed in which the beam spot size is much larger than the area of interest in the target material, in which the lateral straggling of ions (diffusion in 3D) can be ignored [13, 45]. Besides, the sputtering effect from the surface of the target is also neglected during the calculations,as we considered the heavy ion irradiation with relatively higher energies[43],and the depth region of the peak atomic concentration was focused on for the two case studies.

4 Conclusion

The radiation-enhanced diffusion in nickel under selfion irradiation was systematically studied to illustrate the influence of long-term irradiation on implanted ion profiles.The main findings are summarized as follows:

1. The primary radiation damages for nickel self-ion irradiation with ion energies up to 15 MeV were predicted by IM3D.The results are in good agreement with those calculated by SRIM. The cumulative effect of the implanted ions could not be readily ignored with the continued increase in total damage.

2. Three main aspects that contribute to diffusion under irradiation, including ballistic mixing, long-term diffusion, and thermal diffusion are discussed. Diffusion coefficients as functions of temperature and dose rate are obtained. For this, we carefully reviewed the available references on the damage structures (dislocations and voids) of irradiated nickel and temperature-dependent effective sink concentrations were fitted numerically. Such temperature-dependent effective sink concentrations helped to optimize the diffusion coefficients, especially at higher temperatures.

3. Case studies were performed for nickel self-ion irradiation with higher energy irradiation to illustrate the broadening of implanted profiles under long-term and higher-dose irradiation.

The above results and discussion give a systematical view of the effect of radiation-enhanced diffusion on the longer-term atomic evolution under irradiation,and further help to understand the diffusion-related chemical or structural change, e.g., void swelling, under irradiation.

AcknowledgementsThe authors acknowledge the TMSR Supercomputer Center and Shanghai Supercomputer Center for providing computing resources.