CQS550清筛机液压共振问题分析及解决方法

王新磊

摘要：对于一个设备的液压系统，设计工作十分重要，可以避免在后期使用过程中出现意想不到的问题，但是在使用的时候难免会出现各种各样的问题。其中对于液压技术人员经常会感到棘手的问题之一就是：液压系统的振动问题。振动问题不但和液压系统有关，同时也可能和设备的结构有关，甚至和电器控制也有关。本文介绍一个在实际碰到的一个铁路清筛机液压系统的振动故障，通过本次的故障分析和处理的过程，推荐一些适用的解决振动的方法。

关键词：铁路清筛机;液压共振;负载敏感;阻尼;方法

0  引言

流体传动在机械传动系统中有着很多独特的优点，在很多应用场合有着不可替代的作用。但同时流体传动也有很多其特有的问题，这些问题也带给设计者和使用者很多的麻烦。其中之一就是液压系统的故障判断。

在一个液压系统中产生故障，故障的表现形式多种多样。但是由于液压技术的基本形式就是利用流体进行能量传输，而流体又是在一个密闭的容器中才能将能量传递。这样就造成了液压系统一旦产生故障时，很难观察到液压内部到底发生了什么问题，只能根据设备故障的外在现象来判断其产生的原因，比如温度的升高，噪音的产生，速度的变化及压力波动等等。这样就给使用者带来诸多的困难。

在各种的故障中，液压系统的振动又是一个相对复杂的问题。而液压系统的振动对设备的危害又是巨大的，诸如造成：降低液压元件的使用寿命、设备噪音、损害设备的整体强度和设备的使用性能等等。振动（噪音）和液压的漏油现象也是主要限制液压发展的基本问题。而随着现代机械结构日益复杂，运动速度日益提高，振动的危害更为突出。

1  故障现状

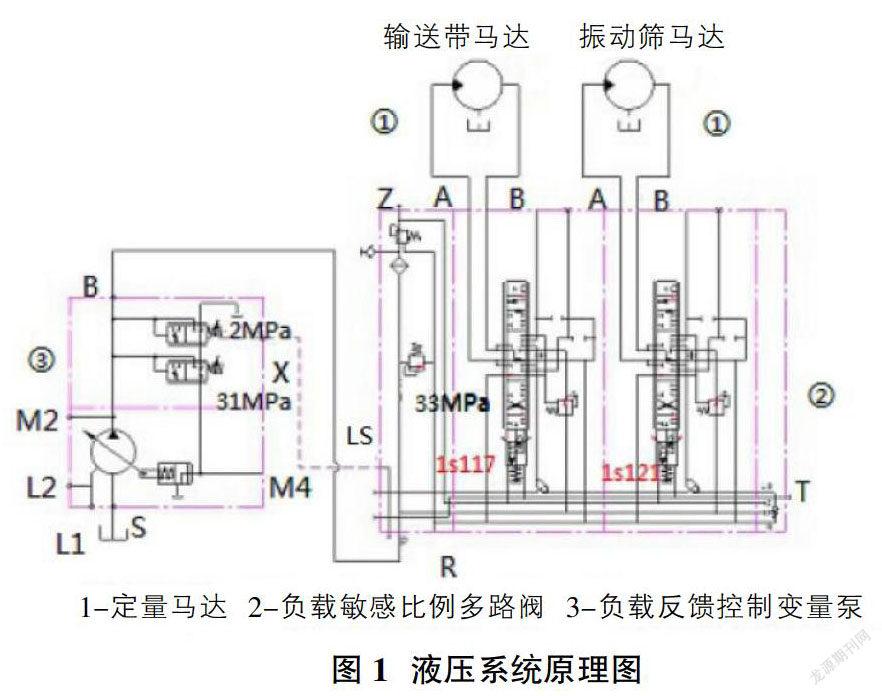
本文分析的液压系统是应用于一台大型的铁路养护设备CQS550清筛机。在这里需要讨论的液压系统，是控制两路液压马达。其中一路是控制设备上的驱动振动筛液压马达，另外一路是控制皮带传输的液压马达。这两个马达需要的压力和流量分别是：（振动筛马达：设定压力31MPa，输入流量75L/min;皮带传输马达：设定压力31MPa，输入流量75L/min）在设备工作的时候两个马达需要同时工作，同时马达的转速需要根据不同的工况进行相应的独立调整。

在液压系统设计时采用了负载反馈系统，使用了负载敏感变量泵和负载敏感比例多路阀来控制这两路马达。通过使用负载反馈多路阀可以实现两个马达的转速不会因为负载的变化而变化，同时也可以保证两个马达在负载不一样的时候也可以同时工作，再配上负载敏感控制的变量柱塞泵，输出的流量根据马达的转速需求提供，不会有多余流量的溢流损失，使整个系统的发热能降低到最小。负载敏感比例阀的集成性又很高，所以使这个系统简洁和安装方便。

在样机调试阶段，这个系统表现很好，得到使用者的认可。很快就决定投入批量生产。

液压系统原理图（如图1所示）：

这个系统在样机试验阶段没有出现任何振动的故障，设备运行平稳，速度调节可靠和稳定。只是在实际交付给用户时用户希望能提供振动筛的驱动力。通过计算泵油足够的流量，于是在不大改动液压系统的情况下最可靠的方法是加大马达的排量。于是就选择了另一品牌的一款马达，直接就投入量产。

更换马达后，扭矩达到了要求，理论上液压系统整体设计满足要求。

该车制造完成在现场调试过程中，出现了一个现象，单独一路马达工作的时候，两个马达的任何一路的压力和流量都稳定可调。但在两组马达同时工作的时候压力表显示压力波动很大，指针大幅摆动，同时马达也产生异响。

2  振动故障的初步处理

对应液压系统的振动故障，可能产生的一些基本振动的因素如下：

①检测油箱内过滤器是否堵塞;

②液压泵是否吸油不畅;

③系统中，如管路和执行元件中是否有空气;

④阀件中的阀芯是否动作灵活、是否有卡死现象;

⑤系统卸荷时是否冲击过大;

⑥液压管件、阀件及油箱等是否按照牢靠。

首先排除了上述在安装过程中可能产生的振动原因，但问题依然存在。既然不是因为安装过程中产生的振动，那么振动源就可能是系统内部产生的。系统内部产生的振动，就要将液压系统转化为一个机械系统来分析。这样分析就要基于機械振动理论。

3  基于机械振动理论的分析

机械设备液压系统简化为如下四个部分：机械结构、变量泵、换向阀、液压马达。

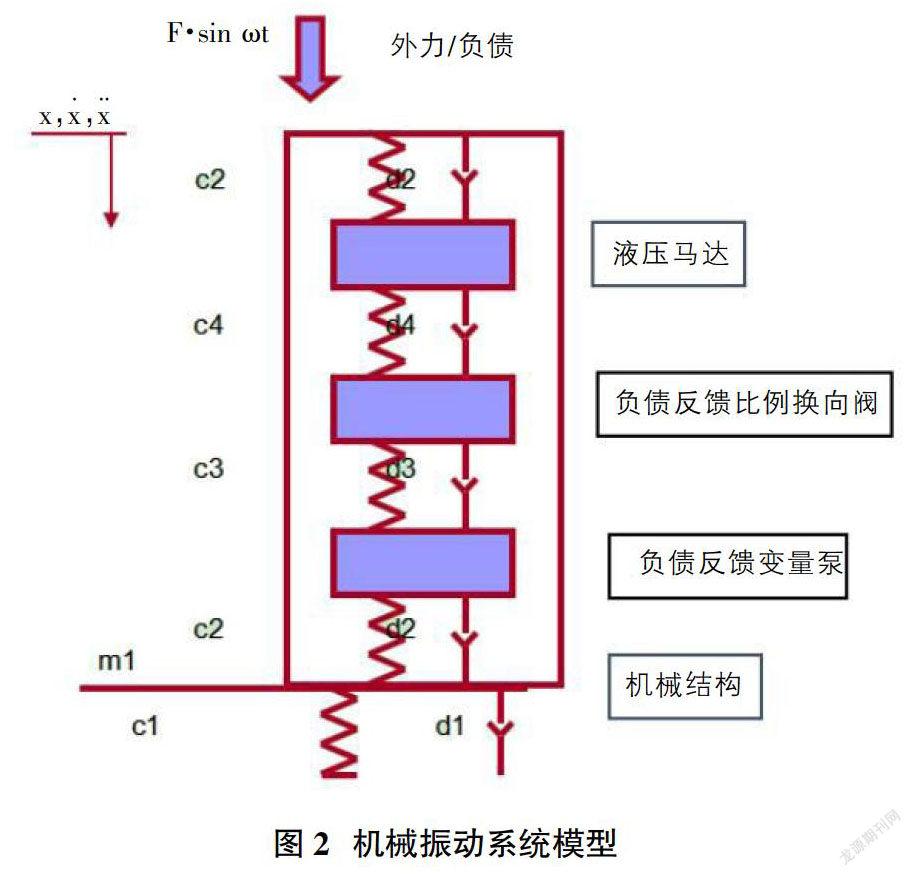
将这个液压系统简化为一个机械振动系统的模型（如图2所示）。

由质量、刚度和阻尼各元素以一定形式组成的系统，称为机械系统。实际的机械结构一般都比较复杂，在分析其振动问题时往往需要把它简化为由若干个“无弹性”的质量和“无质量”的弹性元件所组成的力学模型。

将该液压系统中的液压马达、换向阀和泵简化为机械振动系统。各个部位简化为质点的简谐振动。简谐振动是随时间按正弦函数变化的运动。这种振动可以看作是垂直平面上等速圆周运动的点在此平面内的铅垂轴上投影的结果。它的振动位移为：

式中X为振幅，即偏离平衡位置的最大值，亦即振动位移的最大值;

t为时间;

ω为圆频率（正弦量频率的2π倍）。它的振动速度为：

它的振动加速度为：

振动也可用向量来表示。向量以等角速度ω作反时针方向旋转，位移向量的模（向量的大小）就是振幅A，速度向量的模就是速度的幅值ωA，加速度向量的模就是加速度的幅值ω2A。速度向量比位移向量超前90°，加速度向量比位移向量超前180°。如振动开始时此质点不在平衡位置，它的位移可用下式表示：

式中ψ为初相位。完成一次振动所需的时间称为

周期。

振动方程为：

从公式中可以看出，在外部激振力F的作用，系统产生振荡的决定因素有三个，其一：是元件的质量（m）;其二是元件的弹性系数（d）;其三是元件的阻尼系数（c）。

对于这个液压系统来说，和质量系数相关的参数是：液压马达的运动体（如柱塞副等）、比例换向阀不同位置阀芯的质量和变量泵的运动体（包括控制块中阀芯的质量）。

在这个液压系统中，和弹性系数相关的技术参数有：液压管件、油液、换向阀中弹簧和变量泵中控制器的弹簧。

在本厂试验中，将该系统中的马达再次更换回原排量的马达，该振荡不再出现。说明这个机械振荡系统中影响最大的是质量m这个参数，同时还更换了另一个品牌的比例多路阀，振荡现象也消失了，再次证明质量系数在液压系统中的重要性。

但是前面说了在理论上可以解决很多问题，但是在实际工作中会面临更为复杂的情况。

该铁路设备虽然这个振动现象存在但依然可以工作，只是振动将影响元件使用寿命和现场工人的劳动强度。所以必须得到有效的解决。更换主体元件首先面临的是成本问题，其次是更换了任何元件，安装尺寸就会变化，现场工作量太大。

4  解决方法

4.1 改变阻尼系数减少振动

如果设备中的液压系统出现超过允许范围的振动时，需要采取减振措施。为了减小机械设备本身的振动，可配置各类减振元件。对于液压系统中最常见的减振元件就是阻尼，系统中的阻尼元件减小振幅和延长振动的周期。同时对于系统中的高频振动（小的质量系统），这种高频振动对液压系统非常有害，阻尼元件是一种非常有效的方法。

而增加阻尼根本的原因是改变固有频率。对于标准元件的固有频率理想公式为：

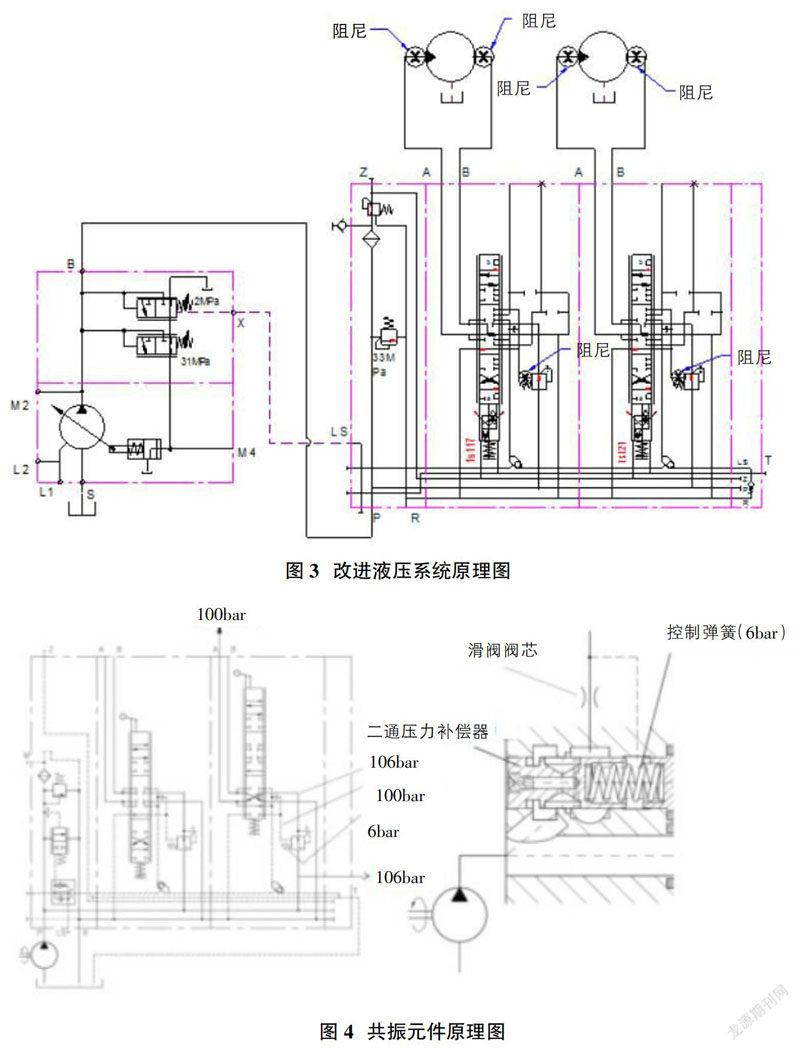
增加阻尼元件其目的也是加大固有频率和负载频率之间的差距。（如图3所示）黑圈的地方增加了阻尼。在不同的阻尼作用下，振动现象是有减少，但是还是不能彻底解决。而且这种阻尼的解决方案没有可重复性。即某种阻尼在某台设备上产生了效果，但在其他设备上可能根本没有作用。而且可能设备某个时间上增加了阻尼有了效果，车辆去工地施工后，振动现象会再次发生。所以必须找一个完全不受外界条件及因素干扰，确实可以彻底解决问题的方案。

4.2 隔断共振元件排除振动故障

基于现场处理问题的条件，原来将减振的方法一直局限在了将两个共振的元件的自有频率拉开。在技术讨论中发现解决共振的问题上还有一个方法，就是隔断两个共振的元件。

对于一组负载反馈比例多路阀，如果需要二路以上执行元件同时工作的话，每片换向阀中需要配置补偿元件，或者叫定差元件，以保证负载压力不同的情况下也可以根据负载需要输出相应的流量。（如图4所示）

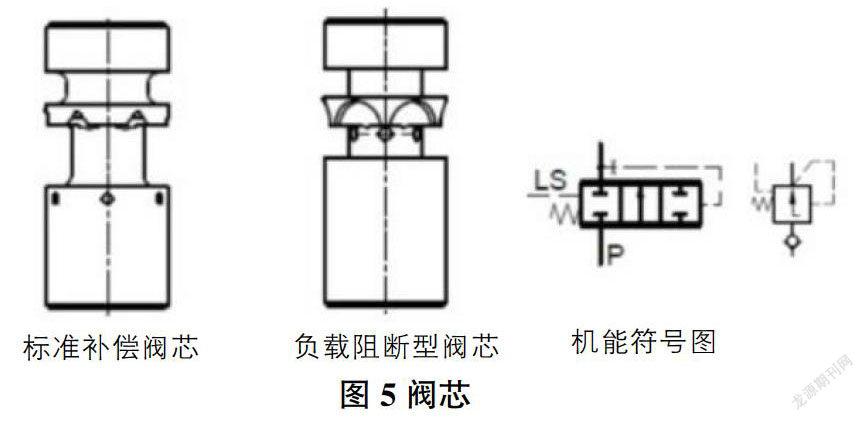
（如图5所示）而换向阀上的这个补偿元件，其作用是平衡同时工作的几组执行元件的压力，这个阀芯是处于常开状态的。两组执行元件间的压力差越大其中压力低的一片的补偿阀开口量越小，相反当两个执行元件间的负载压力接近，阀芯的开口量就越大。在这个设备上就是这个情况，两个马达负载压力很接近，补偿阀处于开口量很大，一旦其中一个马达压力产生波动，振动波很容易通过比例换向阀片传递到另一个马达上，而两路马达和比例阀元件产生共振，实际上在其他油路上增加阻尼元件不会起到太大的减震作用。

在这个比例换向阀上更换了具有负载阻断功能的补偿阀芯，将两条油路在负载接近时和负载差距加大的时候，阀芯都处于向关闭方向运动的趋势。从阀芯的外型图可以看出两个阀芯的最大区别就是遮盖面加大了，这样在中位无补偿的时候阀芯也是处于关闭状态。

将这个阀芯更换上去后，振动现象消失，问题解决。

5  结论

①在設计选型过程中，元件与元件的匹配可能是造成共振的因素。②在本次调试过程中可以感受到，解决共振最有效的方法是改变振动因素中的质量因素。如泵和马达的排量，或阀的规格等。③增加阻尼在很多设备的调试过程中会经常被使用的一种方法，毕竟加上不同的阻尼其成本不高，在很多情况下也好操作。但是在一些工况下可能治标不治本。④解决共振的另外一个方式就是将两个或更多个共振元件间的相通油路阻断，但是必须找到合适的位置。

总之现场处理液压故障过程中，受到现场使用环境的制约因素很多，制定一个确实可行的改进方案需要多方面考虑。

参考文献：

[1]陈浩元.科技书刊标准化18讲[M].北京：北京师范大学出版社，1998.

[2]陈爱萍，赵惠祥，余溢文，等.科技论文插图的可读性编辑加工[J].编辑学报，2015，27（4）：348-350.

[3]张玉.科技文献表格中各项目的科学表示方法——以显著水平比较为例[J].编辑学报，2013，25（4）：339-341.

[4]赵伟.“荷载”还是“载荷”[J].中国科技术语，2013，15（3）：42-43.

[5]周奇.常见语言文字错误防范手册[M].北京：中国标准出版社.