基于ANSYS的升降横移式立体停车库主框架优化设计

孟祥丽 郝亮

摘要：升降横移式立体停车库的主框架部分是典型的钢架结构。钢架结构的特点是在载荷作用下，各杆之间的夹角虽然保持不变，但是会发生整体变形。而主框架的变形对整个立体车库的工作状态影响很大。本文基于ANSYS分析软件对升降横移式立体车库的主框架进行了优化设计。

关键词：立体车库;钢架结构;优化设计

0  引言

主框架、载车板、控制系统、传动系统和安全防护装置五大组成部分构成了升降横移式立体停车库。其中主框架的作用是支撑停车载荷、动力装置和传动系统，通常需要足够的刚度、强度和稳定性，从而保证停車设备的可靠性和安全性。杆系结构中，刚架结构的典型特征是各杆端之间为刚性连接。升降横移式立体停车库的主框架就是典型刚架结构中的一种。整个立体停车库的刚架主要是由等截面的线性杆件（梁和柱）刚性连接而成，而梁、柱之间为刚性连接的结构一般称为钢架结构。在载荷作用下会发生整体变形，但是各杆之间的夹角保持不变是钢架结构的特点。而主框架的变形对整个立体车库的工作状态影响很大。因此，本文基于ANSYS分析软件对升降横移式立体车库的主框架进行的优化设计是非常关键的。

1  建立有限元模型

1.1 主框架数据

横梁、纵梁、立柱、立撑和支撑杆构成了钢结构框架的主体，不考虑细节，主体部分的参数如表1所示。

1.2 立体车库钢结构有限元建模

本次分析梁柱的构造单元选择beaml88。材料的弹性模量、泊松比、密度分别为2.1e11、0.3和 7800kg/m3。我们采用参数化建模的方式构建该有限元模型，并且在前处理模块中输入各个梁的截面参数，就是为了方便后续立体车库模型的优化设计。将创建的节点显示在图形窗口中，然后按照几何关系，把节点连接成单元，其中节点数为6498，单元数为3278。

2  立体车库钢结构的受力分析

考虑到车库的真实受力情况特别复杂，因此我们先设定一些假定条件，然后再进行有限元分析，其中假定条件包括以下几个方面：①假定车库结构无初始缺陷和变形; ②停车库与其它建筑物相对独立;③结构阴面与阳面的温差引起的热应力不予考虑;④不考虑地震载荷与风载的作用[1]。

我们把立柱底端设定为全约束状态可以很好的模拟车库立柱与地面之间的地脚螺栓连接。考虑到刚架自身重量相对较重，所以自重必须予以考虑。本次设计中总载荷为2000kg，其中包括车重1500kg，载车板及车位架重500 kg，即总重19.6kN。横梁上的载荷是通过车位架上面4个滚轮传递过来的，而车位架上的载荷主要是钢丝绳上承受的载车板及车的重量。升降横移类机械式停车设备对车位载荷有一定要求，即前后横梁各自承受的总重量的分配比例为6：4，所以前横梁和后横梁每个车轮承受的重量分别为6000N、4000N。车轮间距为1.5m[2]。

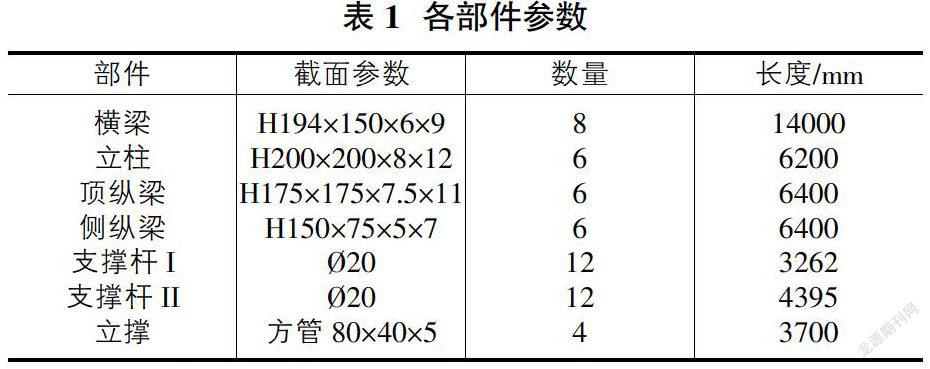
通过有限元分析得到满载时立体车库钢结构受力情况：最大等效应力67.4MPa，最大位移4.189mm，质量为8127kg，如图1所示。

本次分析结果的校核标准[3]选用《起重机设计规范》GB/T 3811-2008。根据标准对起重机类低定位精度设备的要求，假设F为主梁的垂直静挠度，S为起重机跨度，那么两者之间的应满足F？燮S/500的关系，算下来垂直静挠度F应控制在12.6mm以内;另外计算得出许用应力[]=MPa=158.78MPa（其中强度安全系数选取为1.48）。

显然，初始状态下满载立体车库框架的挠度与强度均满足要求，且有些富余。

3  主框架优化设计

3.1 右侧斜拉杆位置优化

由图1可知，由于斜拉杆与竖撑在横梁连接点比较接近，容易发生应力集中的现象，另外中立柱与右立柱之间跨度又较大且没有支撑，因此会加剧变形。为此首先选择对两侧斜拉杆的连接位置进行优化设计，就是为了达到减小横梁变形的优化目标。

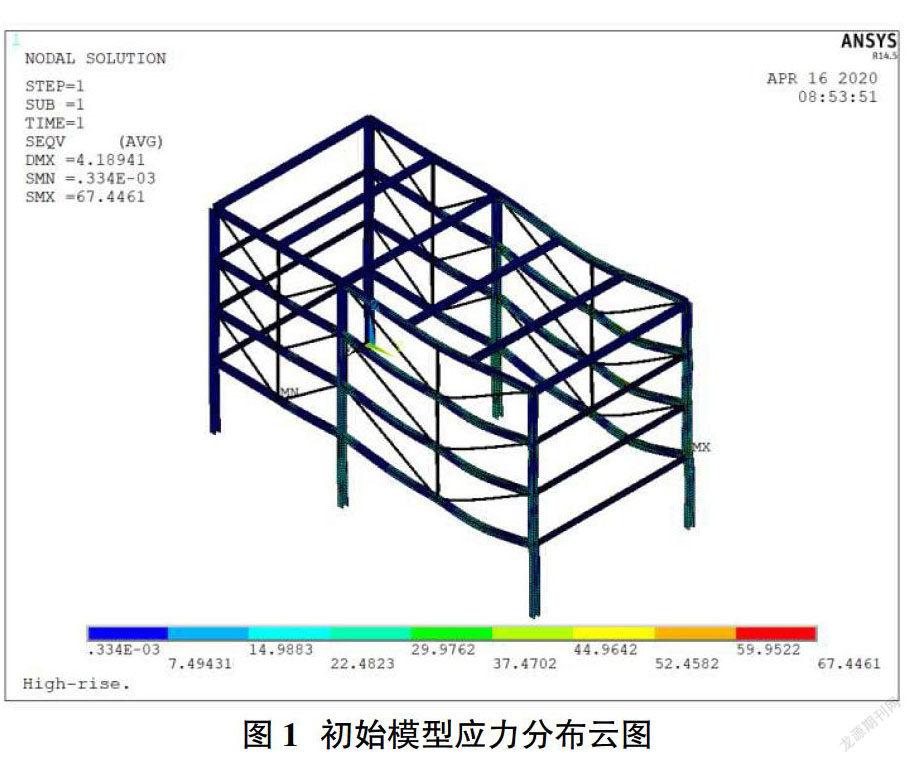
取前面第一层横梁右侧做局部分析可以使分析更加方便，设定斜拉杆在第一层横梁的连接处与横梁中点的距离为A，初始情况下令距离A的取值为100。通过变换A的取值，得到新的模型，汇总新模型的分析结果数据相对初始情况下的最大位移变化规律，得出图2的曲线;同理汇总新模型的分析结果数据相对初始情况下的最大等效应力变化规律，得出图3的曲线。

由上述两图分析可知，最大等效应力为54MPa，发生在A=1m处，此时最大位移减少为2.54mm，相对初始模型减少了38%，优化效果比较明显。

3.2 左侧斜拉杆位置优化

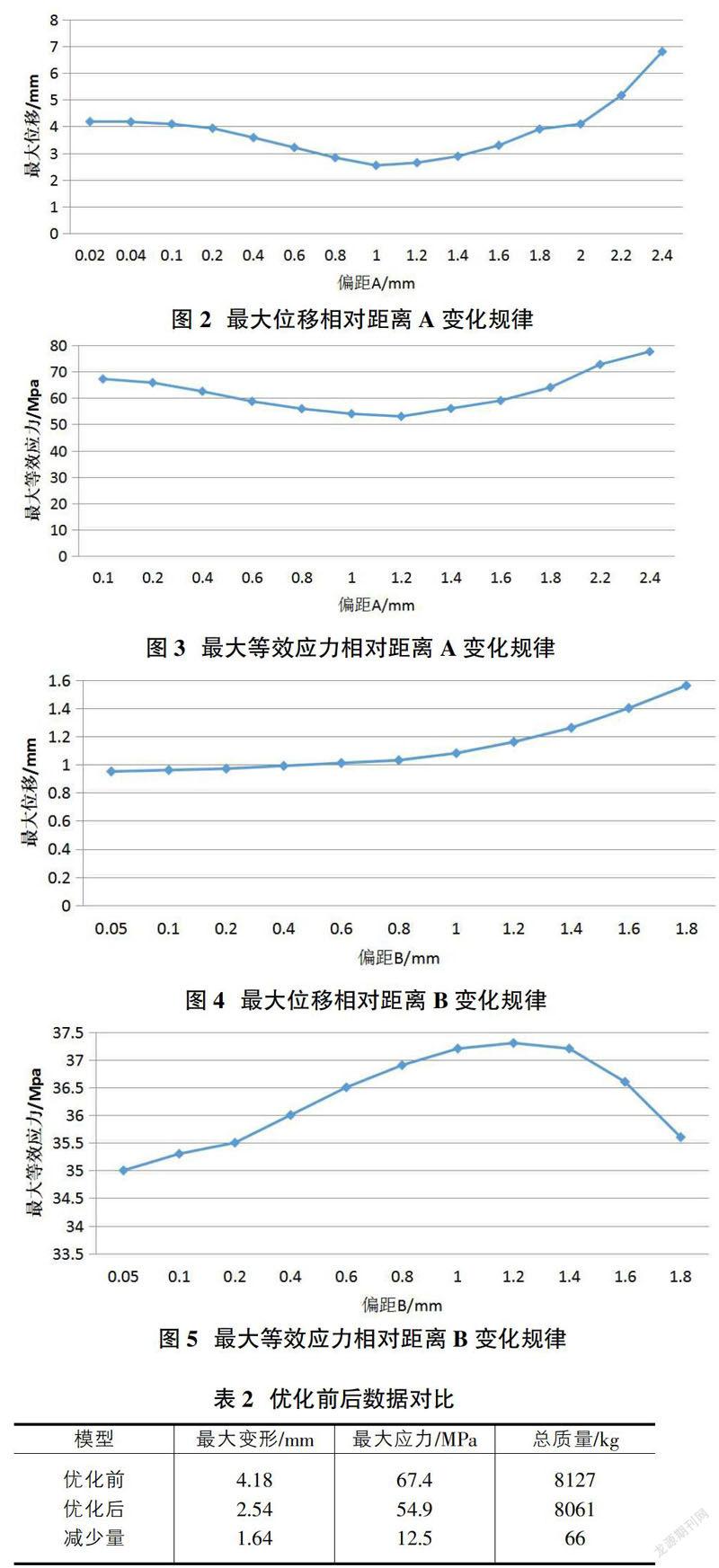
令A取上述最优解1m，取前面第一层横梁左侧做局部分析，设定斜拉杆在第一层横梁的连接处与横梁中点的距离为B，初始情况下B=50，通过变换距离B的取值，得到新的有限元模型，并对新模型进行有限元分析，得到最大位移相对距离B的变化规律，见图4，同理得到最大等效应力相对距离B的变化规律，见图5。

由上述两图可知，偏距B最优解出现在B=0.05m处，该模型下最大位移为0.95mm，局部最大等效应力为35MPa，最大位移与最大等效应力都比较小。

将以上局部结构优化的结果应用到整体钢结构中，并重新进行有限元分析，得到最大等效应力为54.9MPa，最大位移2.54mm。

将模型优化前后数据对比如表2所示。

通过对表2数据进行分析，优化后整体钢结构性能有了提升，各指标也有了一定的优化，最大变形量降低了39%，最大应力减少18.5%，质量减少0.8%。最大变形量大幅减少，实现了优化目标。

4  小结

本文对升降横移式立体车库的主框架进行的有限元分析是借助ANSYS软件，并对其左右两侧斜拉杆连接位置进行了优化设计，通过位移及应力曲线图的变化规律得出左右斜拉杆的最优位置。将两侧局部结构优化结果应用到整体钢结构中，并计算最大位移及最大等效应力，通过与初始模型的最大位移及最大等效应力云图进行对比，最大变形减少39%，最大应力减少18.5%，质量减少0.8%，可以看出优化后整体钢结构性能得到提升，尤其最大变形量大幅减少，在原有基础上实现了各指标的优化。

参考文献：

[1]张丽，于长有.升降横移式立体车库钢结构框架受力分析及优化[J].绥化学院学报，2016，36（5）：139-141.

[2]荆友录，国兴玉.立体车库钢结构骨架的受力分析与结构优化[J].山东交通学院学报，2004，12（3）：1-4.

[3]郭鹏.基于CAE的垂直循环立体车库结构设计研究[D].济南：山东大学，2007.