中国传统益智游戏背后的数学知识
孙文希
七巧板、九连环、华容道,这些中国传统的益智游戏你玩过吗?这些游戏给我们带来了快乐,也把先人的智慧流传了下来,它们的背后,都有一个坚实的后盾——数学。
七巧板——勾股定理
七巧板的历史可以追溯到我国先秦的古籍《周髀算经》,书中记载有正方形切割术,并由此证明了勾股定理,《周髀算经》中的正方形切割术是将大正方形切割成四个同样大小的三角形和一个小正方形,这还不是我们现在熟悉的七巧板。
现在的七巧板是经过了一段历史演变过程的,宋朝黄伯思发明了一种用6张小桌子组成的“燕几”——请客吃饭的小桌子,后来有人把它改进为7张桌子组成的燕几,可以根据吃饭人数的不同,把桌子拼成不同的形状,比如3人拼成三角形,4人拼成四方形,6人拼成六边形……这样用餐时更加灵活方便,后来,宋代的燕几图到明代发展为蝶几图,到清初再演变成七巧图,到现在已经有2500多年的历史了,大约18世纪,七巧板流传到海外,被欧洲人称之为“东方魔板”“唐图”,之后,七巧板得以发展、改造和创新,成为一种世界性的智力游戏。
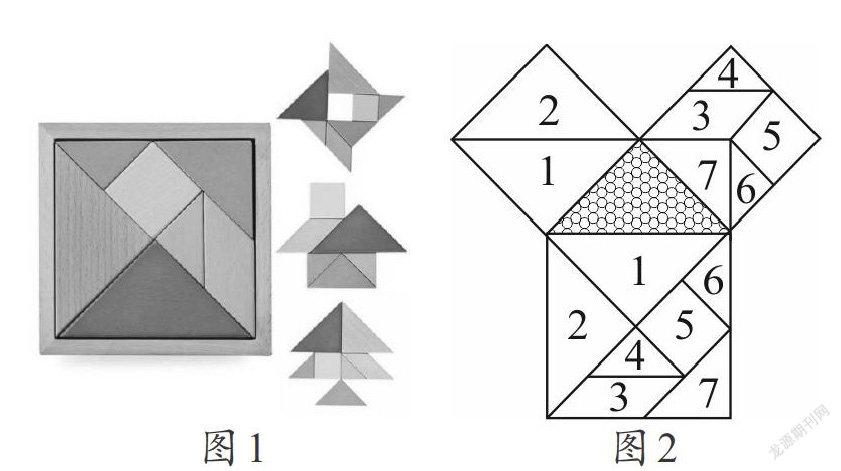
七巧板完整图案为一正方形(圖1):五块等腰直角三角形(两块小三角形、一块中型三角形和两块大三角形)、一块正方形和一块平行四边形,利用七巧板可以拼成许多图形,包括人物、动物、植物、建筑物、文字等,据说有记载的图形已超过1000种,你知道七巧板也可以用来证明勾股定理吗?图2是用两副同样大小的七巧板拼成的,在图中,下部平放的正方形由一副七巧板拼成,上部斜放的2个正方形由另一副七巧板拼成,这三个正方形内侧围出一个直角三角形,因为斜边上的大正方形面积等于两条直角边上的小直角三角形面积之和,所以我们不难得出这样的结论:直角三角形斜边长的平方等于两条直角边长的平方和,这正是勾股定理的内容。
九连环——递归原理
九连环主要是由一个金属框架和九个圆环组成:每个圆环上连有一根直杆,而这根直杆则在后面一个圆环内穿过,九根直杆的另一端相对固定,它的玩法就是要将这九个圆环从柄上解下来,西汉大才女卓文君的诗作里就曾提及九连环:“一别之后,二地悬念,只说三四月,又谁知五六年,七弦琴无心弹,八行书不可传,九连环从中折断,十里长亭望眼欲穿,百思想,千系念,万般无奈把郎念,”这说明九连环至少有近两千年的历史,
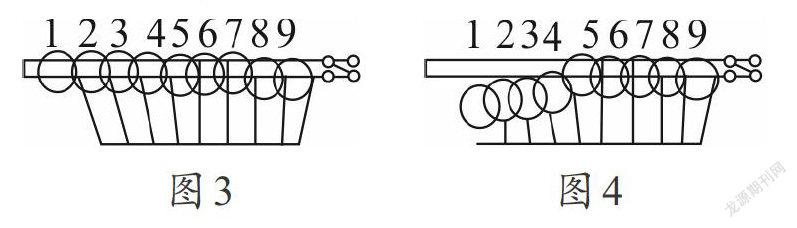
九连环的每个环互相制约,只有第一环能够自由上下,要想下/上第n个环,就必须满足两个条件(第一个环除外):1.第n-1个环在架上;2.第n-1个环前面的环全部不在架上,先以第9环为目标,先拆下它,简化为拆一个8连环,接着再以第8环为目标,拆下它,简化为拆一个7连环……以此类推,直至全部拆解,解下九连环必须要从后面的环开始下,而先下前面的环,是为了下后面的环,前面的环还要装上,不算是真正地取下来。
九连环的游戏规则是不是让人觉得跟递归原理有联系呢?递归的基本思想是把一个大的问题分解为一个规模较小的问题,由这些较小问题的解,得出大问题的解,而这些规模较小的问题,用同样的方法分解成更小的问题,由更小问题的解,得出较小的问题的解,一层层下去,一般最后总是可以分解到可以直接求解的小问题,这就和解九连环的规律一模一样。
解开九连环至少需要341步,按每步耗时1-2秒计算,需要5到10分钟,如果是八连环,需要170步,大约4分钟可以解开;十连环需要682步,20到40分钟才能解开,而一个三十三连环,每秒钟一步,也要180多年才能解完呢。
华容道——组合数学
曹操败走华容道是《三国演义》中的一个著名故事,华容道游戏即取材于此,华容道属于滑块类游戏,就是在一定范围内,按照一定条件移动一些称作“块”的东西,最后满足一定的要求,滑块类游戏究其起源,最早可追溯到中国古代的“重排九宫”,产生于出现河图洛书的远古时代,有数千年历史。
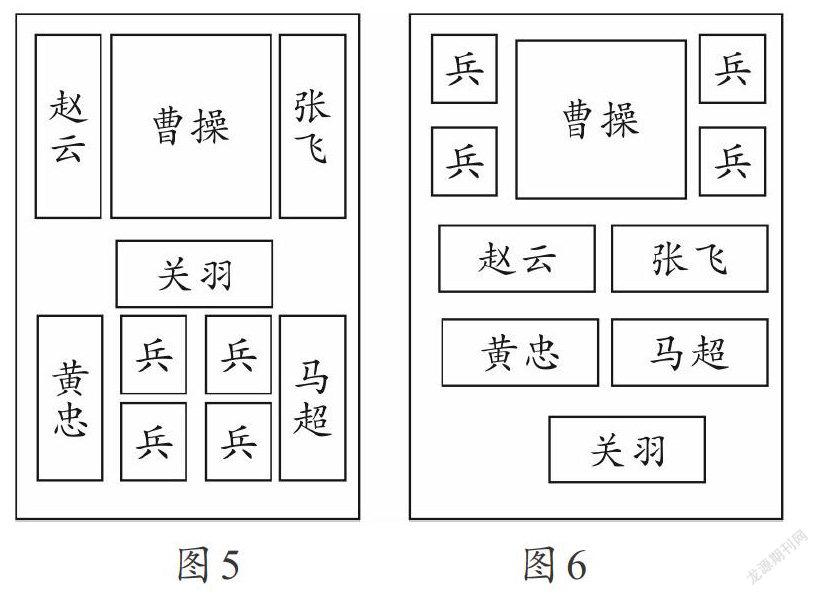
华容道有几十种布阵方法,如“横刀立马(图5)”“近在咫尺”“过五关(图6)”“水泄不通”“小燕出巢”等,由华容道的诸多排列方法,可以衍生形成十分复杂的棋局,棋盘上仅有两个小方格空着,玩法就是通过这两个空格移动棋子,用最少的步数把曹操移出华容道,华容道的魅力在于,要预先想出好几步才能走出最近的一步,所以,华容道其实包含着非常复杂的排列组合计算。
早在1952年,我国数学家许莼舫在《数学漫谈》一书中对华容道游戏就做了细致的研究,他在试验的基础上不断探索,总结出了100步的解法和几条游戏规则,可以概括为:四个小兵不能分开,一定要两两组合在一起;关羽、曹操等大将在移动的过程中,前面需要两个小兵开路;曹操一旦移动,后面必须有两个追赶的小兵,1964年,《科学美国人》杂志上公布了美国数学家马丁,力Ⅱ德纳的新解法,破解了华容道最常见的阵法“横刀立马”,仅81步便可成功,这也是华容道已知的最优解法,因此,华容道与法国人发明的独立钻石、匈牙利人发明的魔方被并称为“智力游戏界的三个奇迹”。

