管道环焊缝缺陷漏磁检测仿真模拟

毛瑞麒 马梦想 饶连涛 许志军 苏林 储玲玉 徐杰

摘要：基于漏磁检测技术基本原理，采用有限元方法，应用COMSOL软件对管道环焊缝及焊缝处常见缺陷磁化后产生的漏磁场进行了仿真模拟，得到描述磁场分布特征的磁通密度径向和轴向分量分布曲线。通过改变焊缝余高以及焊缝处凹坑、错边和咬边的几何参数，得到了不同缺陷类型在不同尺寸下的磁场分布。结果表明：管道环焊缝磁场分布呈增厚特征，且随着焊缝余高的增加，磁通密度径向和轴向分量值均明显增大;焊缝与其中心缺陷呈两者复合的磁场分布特征。焊缝中心凹坑磁场分布呈减薄特征，且磁通密度轴向和径向分量峰的峰宽均随凹坑直径的增加近线性增大;随着错边量的增加，缺陷处磁通密度分布曲线的峰值均明显增大;随着咬边深度的增加，咬边位置的磁通密度减小。

关键词：管道环焊缝;径向励磁;焊缝缺陷;磁通密度;有限元模拟

中图分类号：TG115.28文献标志码：A文章编号：1001-2303（2020）11-0028-09

DOI：10.7512/j.issn.1001-2303.2020.11.06

0 前言

焊接過程受焊道设计、工艺、材料、环境等多方面因素的影响，不可避免地会出现各种缺陷。这些缺陷的存在可能会造成管道开裂、油气泄露甚至爆炸等严重事故[1]。为了保证管道安全运输，需要定期对其进行无损检测和安全评估。目前常用的无损检测方法有涡流检测、射线照相检测、超声检测、磁粉检测和漏磁检测法等。其中漏磁检测技术具有检测灵敏度高、不需要耦合剂、受外界干扰小、检测速度快且易实现自动化，更适于大面积、长距离管道的快速检测，是目前国内外应用最为普遍的管道内检测技术[2-5]。

文中基于漏磁检测原理，应用COMSOL软件，采用径向励磁方法对管道环焊缝及焊缝处常见缺陷进行三维仿真，得到了不同焊缝缺陷的磁通密度径向和轴向分量的分布规律，为管道焊缝缺陷漏磁信号特征识别提供理论依据，同时对径向励磁在铁磁性材料漏磁检测中的可行性和适用性进行了理论探讨。

1 漏磁检测技术的基本原理

传统的管道漏磁检测以轴向励磁检测为主。由于铁磁性材料磁导率高，当管道被磁化时，磁感线会被约束在管道内部，且几乎没有磁力线从表面穿出，被检测工件表面几乎没有漏磁场。若管道存在裂纹、凹坑等切割磁力线的缺陷，由于缺陷处磁阻远大于管材，就会有部分磁感线从管壁漏出，从而形成漏磁场。利用管道上方的磁敏传感器可以检测到相关信号变化，从而判断缺陷的存在和相关特征[6-10]。

为了使检测器检测效果达到最佳状态，传统漏磁检测技术需要将管道等铁磁性材料磁化至饱和或近饱和，这可能会带来很多问题。首先，将管道磁化到饱和后退去磁场会有很大的剩磁，会对二次检测造成严重干扰;其次，轴向励磁很多时候采用线圈磁化，要形成强磁场则需要很大的安匝数，从而使得电流的热效应不可忽视，长时间工作可能会对检测装置的寿命产生一定影响[11-12]。

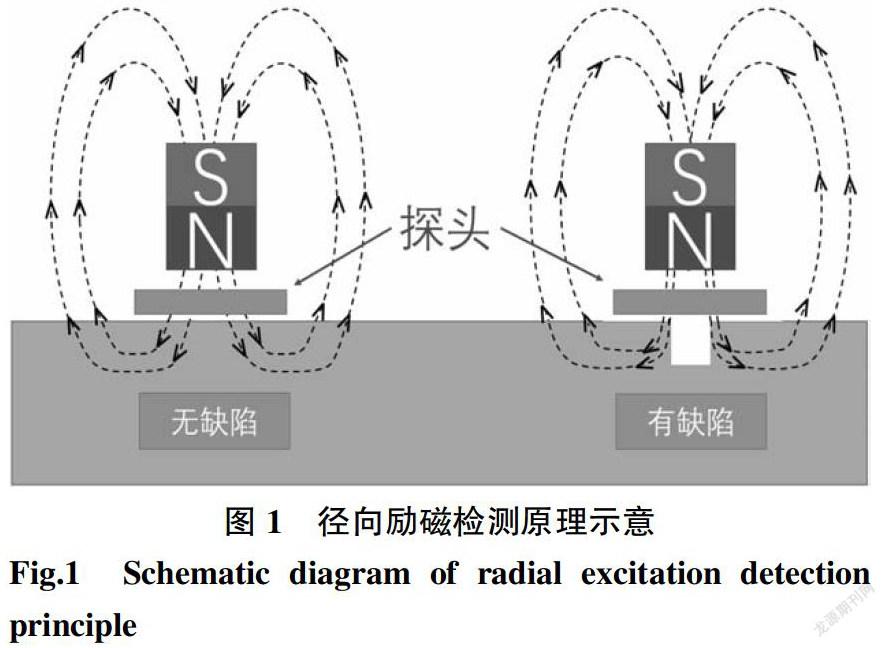
径向励磁和轴向励磁类似，其基本原理如图1所示，通过在检测器探头内部集成一块永磁铁，检测器在管道内运行过程中管道内表面被永磁铁磁化。径向励磁不同于轴向励磁之处在于：径向磁感线垂直于管道轴向方向并穿过表面回到磁铁。对于正常的无缺陷管道，其内表面是光滑的平面，在探头磁铁和管道内表面之间会形成相对稳定的磁场;而当管道存在缺陷时，原有磁场的分布状态会被改变，通过在磁铁和管壁间安装霍尔元件可采集探头位置管道内表面的磁场信号，通过进一步比较分析磁场分布特征可判断缺陷的存在及特征，既可达到检测的目的，又不需要采用强磁场对管道进行磁化[13]。

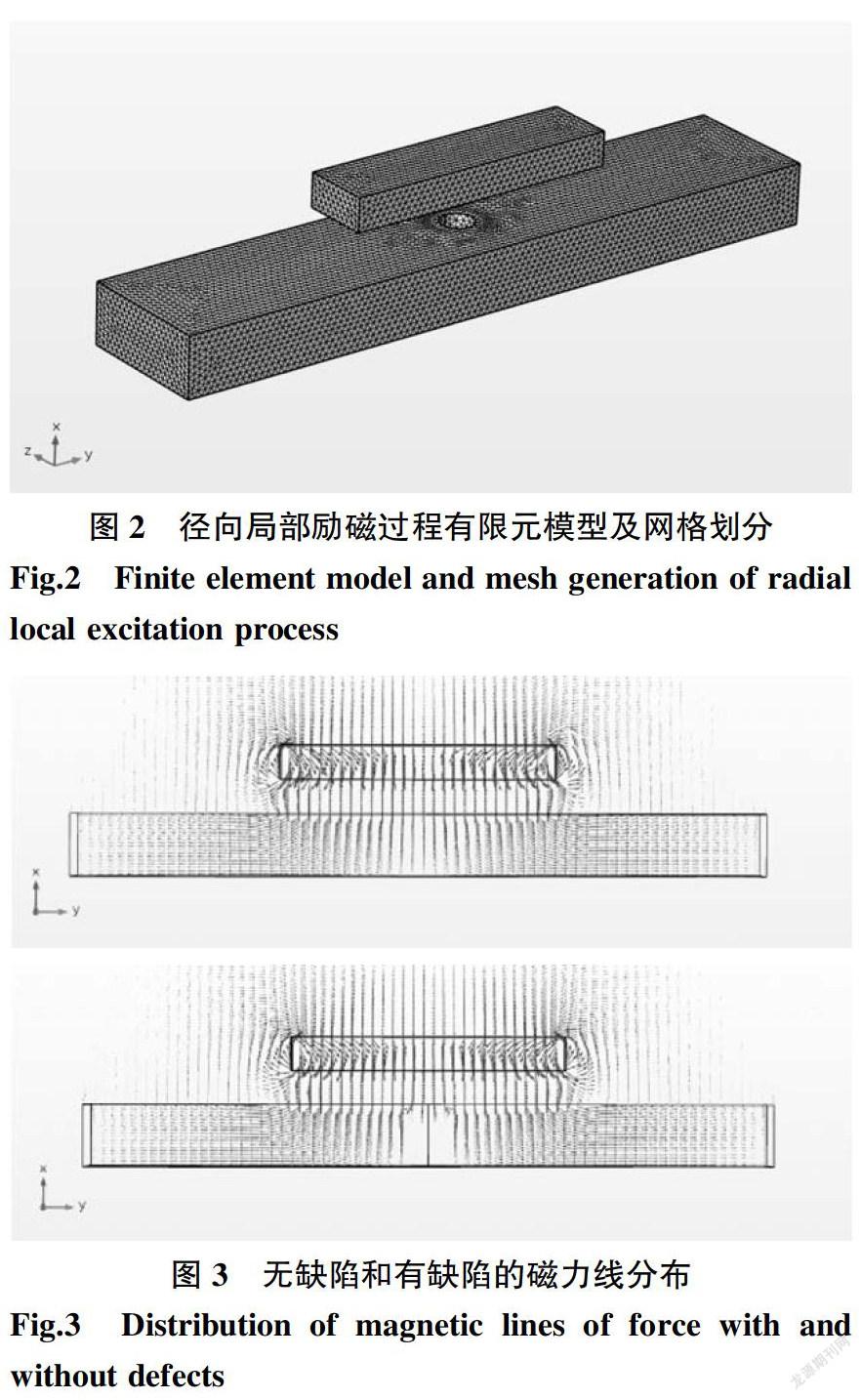
为了验证上述方法的可行性和有效性，下面采用有限元模拟方法对上述径向励磁过程进行仿真分析。上述过程的有限元模型如图2所示（考虑仅为验证该方法的可行性，这里采用平板代替管道进行几何模型的简化分析），无缺陷和有缺陷时有限元计算得到的磁力线分布如图3所示，相应的磁通密度分布曲线如图4所示。设模型中管子径向（即壁厚方向）为坐标轴x方向，轴向（管道长度方向）为y方向，即Bx为磁通密度径向分量，By为磁通密度轴向分量。

由图3可知，无缺陷时，管体经过励磁后，由于其磁导率远大于空气，因此绝大部分磁通从管体内通过构成回路。在距平板上表面1 mm处沿平板长度方向提取磁场分布，结果显示其径向分量Bx为一恒定值（见图4a，磁力线均匀通过管体形成稳定磁场），轴向分量By为一条近乎为零的水平线（见图4b）;而有缺陷时，缺陷边缘处磁力线发生明显畸变（见图3），并且在相同提离值位置可以看到不同的磁场信号，有缺陷时磁通密度径向分量Bx呈一典型的凸峰，轴向分量By则沿缺陷中心呈一负一正的两个对称峰。可见，采用径向励磁方法模拟有缺陷的漏磁通是可行且有效的。

2 环焊缝及其中心缺陷有限元模型

2.1 三维几何模型

焊缝及其中心凹坑、错边和咬边缺陷的三维几何模型如图5所示，为便于比较分析，采用尺寸为150 mm×50 mm×9 mm的平板代替管道进行有限元建模与计算分析;永磁体尺寸40 mm×30 mm×5 mm，永磁体与板面距离为5 mm。同时，模型中考虑了焊缝表面余高的影响。

2.2 材料属性

由漏磁检测原理可知，模型中的关键部件有管道、永磁体和空气罩，模型中需分别对这些部件的材料属性进行定义。文中以Q235管材为研究对象，已知空气的相对磁导率大小为1.0，磁铁采用永磁体，相对磁导率为1.045、矫顽力为960 000 A·m-1。

2.3 网格划分

在有限元模拟计算中，网格数量的多少将影响计算结果的精度和计算规模的大小。一般来讲，网格数量增加，计算精度会有所提高，但同时也会增加计算量喝计算时间。有限元网格模型如图6所示，焊缝处采用均匀致密的网格以提高计算精度，远离焊缝中心部分则采用较疏的六面体扫掠网格来缩短计算时间。

3 结果分析与讨论

3.1 管壁增厚和减薄模型磁场分布特征

为了探究径向励磁下的磁场分布特征，首先设计了直径2 mm的凸起和凹坑来分别模拟管壁增厚和减薄情况下的磁场分布，如图7所示，其中增厚模型取提离值位于管道上表面2 mm处，减薄模型取提离值高于管道表面1 mm处。通过计算分别得到Bx和By的分布曲线以及磁感线分布。

管壁增厚情况下的磁通密度分布曲线如图8所示。可以看出，在径向励磁方式下，磁通密度径向分量Bx分布曲线在增厚处呈现一个明显的凹峰（见图8a），极性为负，其值增大，即在管壁增厚处磁场会有明显的增强。这是由于管壁增厚处材料的相对磁导率远大于空气，有助于磁力线穿过，从而使此处的磁力线聚集，进而增强磁场。By在增厚处呈现以原点为中心先正后负的两个中心对称峰（如图8b）。

增厚模型的磁力线分布如图9所示。可以看出，在无缺陷区域，磁力线方向和管道表面垂直，分布均匀，此时，Bx为一恒定值，By几乎为零。而在管壁增厚区域，磁力线的分布密度明显增大，并向中心聚拢。将磁力线沿坐标轴分解可以看出：其径向分量垂直于管壁向下（極性为负），由于聚集作用使其磁通密度大于无增厚区域;磁力线矢量分布图（见图9b）中，轴向分量则先正后负，与图8b的磁通密度分布曲线结果相吻合。

壁厚减薄情况下的磁通密度分布曲线如图10所示。由图10可知，减薄的磁感应强度分布和增厚时相反，Bx为一个凸峰（见图10a），极性为负，其值减小，即在减薄处磁感应强度减小。这是由于减薄使得原本相对高磁导率的管材被相对磁导率非常低的空气（或其他介质）充满，使得磁场在减薄处发生畸变，从而导致磁感应强度降低，这与文献[14]中的结果是一致的。By呈现先负后正以原点为中心的两个对称峰（见图10b）。

减薄模型的磁力线分布如图11所示。可以看出，在管壁减薄区域，磁感线的分布密度明显减小，同时呈现由中心向两边发散的趋势。同样将磁力线沿坐标轴分解可知，径向分量垂直于管壁向下（极性为负），由于发散作用使其密度小于无增厚区域;轴向分量先负后正，与图10b结果吻合。

3.2 焊缝余高

管道焊接时，焊缝表面会存在一定的余高（即超出焊缝表面焊趾连线部分焊缝金属的高度），不同标准根据焊缝级别不同对余高值有不同的要求，但一般不超过3 mm。为了便于比较分析，保持管道参数和焊缝宽度等参数不变，分别将焊缝余高设定为1 mm、2 mm和3 mm，并与无焊缝余高时的结果进行比较。提取距管道平面高度3 mm处的磁通密度，得到不同余高下的Bx和By的分布曲线，如图12所示。

由图12可知，有焊缝余高时的磁通密度径向分量和轴向分量分布特征分别与3.1节中增厚模型的Bx和By曲线形状类似，即焊缝处余高的存在使得Bx呈现一显著的凹峰，极性为负，其值增大（见图12a）;By呈以焊缝中心为对称的先正后负两个峰（见图12b）。并且随着焊缝余高的增加，Bx和By的峰值大小均明显增大。

为便于比较环焊缝不同缺陷的磁通密度分布规律，统一取焊缝余高为2 mm，提离值距管道表面2 mm。

3.3 焊缝中心缺陷的磁场分布特征

针对常见的焊缝缺陷——凹坑、错边和咬边的磁场分布进行仿真模拟，并通过改变缺陷尺寸进一步分析不同参数对Bx和By分布曲线的影响规律，同时与无缺陷情况进行对比，探讨径向励磁条件下不同焊缝缺陷的磁场分布特征。

3.3.1 凹坑

为了简化模型，将凹坑近似为球形，球心位于焊缝中心，球的半径沿管子壁厚方向简称为凹坑深度。为了分析凹坑深度对磁场分布的影响，建立了直径分别为2 mm、4 mm、6 mm和8 mm的凹坑进行比较分析，得到了凹坑处的Bx和By分布曲线（见图13）以及磁通密度分布云图（见图14）。

由图13可知，无缺陷时，Bx和By表现为典型的焊缝余高磁场分布特征。当焊缝中心有凹坑缺陷时，Bx为两凹峰中间夹着一个凸峰，且两凹峰对称分布于中间凸峰两侧。By为两正两负四个峰且对称分布于焊缝中心（亦是凹坑中心）两侧。

结合上文3.1和3.2节的分析可知，图13a中Bx分布曲线中位于外侧的两个凹峰对应焊缝余高（增厚特征），中间的凸峰则对应中心的凹坑（减薄特征）;同理，图13b中By分布曲线中外侧一正一负的两个峰对应焊缝余高（增厚特征），内侧的一负一正两个峰则对应凹坑（减薄特征）。可见，图13是焊缝处余高和凹坑缺陷磁场复合的结果。另外，由图13还可知，Bx中间凸峰边缘的宽（见图13a）和By中间一负一正两个峰的峰宽（见图13b）正好对应其相应凹坑的直径。由此可见，焊缝中心凹坑的Bx和By分布曲线的峰宽可以较好地定量表征凹坑大小。

另外，随着凹坑直径的减小，其磁通密度径向分量Bx所对应的中间凸峰的边缘峰值增大（见图13a，Bx极性为负，其中间凸坑峰值大小随凹坑直径减小近线性增大），凸峰峰值无明显变化;轴向分量By所对应的一负一正两峰的峰值亦随凹坑直径减小近线性增大（见图13b）。

由图14可知，磁通密度在凹坑边缘处明显聚集。当凹坑直径较小时，磁通聚集位置距提离值较近，信号越强（峰值愈高）;而凹坑较大时，此时材料减薄严重，磁通密度聚集位置距离提离值较远，信号变弱（峰值减小）。

3.3.2 错边

管道在焊接时常常会出现对口不准的情况，焊后就会存在错边，为了研究不同错边量下磁场分布的规律，选取了错边量分别为管道壁厚的5%、10%、15%和20%进行计算分析，得到Bx和By分布曲线，如图15所示。

由图15可知，无错边时，Bx呈以焊缝中心为对称的凹峰;By则以焊缝中心为对称呈一正一负两个对称峰。相比无错边焊缝，错边的存在导致磁通密度分布曲线最明显的变化在于焊缝中心两侧的磁场分布不再对称。且随着错边量的增加，Bx和By的对称中心均向左偏移，同时峰值均近线性增大，这与文献[15]中采用轴向励磁模拟的结果是一致的。另外，由漏磁检测原理不难得知：错边的发生使得焊缝中心两侧的几何形状左右不对称，导致原本对称分布的磁力线产生畸变，从而产生磁场信号的变化。

3.3.3 咬边

咬边通常是焊接时由于操作不当或选材不当，导致沿焊趾部位产生沟槽而造成的缺陷。实际情况下的咬边缺陷更为复杂且不可控。文中基于图5e的几何模型，选取咬边深度分别为管道壁厚的5%、10%、15%和20%进行模拟，通过计算得出不同咬边深度的Bx和By分布曲线（见图16）以及磁力线分布（见图17）。

由结果可知，与焊缝中心凹坑的磁通密度分布类似，图16的分布曲线也是焊缝和咬边缺陷磁场复合的结果，其中Bx中间的凹峰和By中间一正一负两峰对应的是焊缝的磁场特征信号。而Bx的峰肩和By峰趾处对应的是咬边的磁场特征信号（见图16中咬边位置）。由咬边的几何模型（见图5e）可知，咬边属于减薄缺陷，其结果与3.1中的结论一致。

咬边的磁通密度径向分量和轴向分量分布曲线的整体趋势和无咬边焊缝无明显差异，但不同咬边深度时峰值有所变化：随着咬边深度的增大，咬边位置处Bx和By对应的峰值均减小，说明咬边越深，磁场信号愈弱;同时，Bx中两峰间距离和By正负峰的间距均减小，向焊缝中心聚拢。

由图17可知，磁力线在咬边位置上方有明显的减弱，这是由于咬边本质上属于局部材料减薄，使磁通密度减小，故而信号减弱。

4 结论

文中运用COMSOL有限元软件采用永磁体径向励磁方式对管道环焊缝及其常见的错边、咬边和凹坑等缺陷的磁场分布特征进行了模拟仿真，结论如下：

（1）在文中励磁方式下，管壁增厚的磁通密度分布径向分量Bx呈现一个显著的凹峰;By为先正后负的两个中心对称峰;相同励磁方式下，壁厚减薄则相反，即Bx为一凸峰，By呈先负后正的两个中心对称峰。

（2）管道环焊缝的磁场分布呈典型的增厚特征，随着焊缝余高的增加，Bx和By的峰值均明顯增大，但其所对应的峰值位置不变。

（3）对于焊缝缺陷：焊缝中心凹坑的磁场分布呈典型的减薄特征，且Bx和By两峰的峰宽可以较好地定量表征凹坑大小;错边使焊缝中心两侧的磁场分布不均匀，随着错边量的增加，Bx和By的对称中心向一侧偏移，且两者的峰值均近线性增大;对于咬边缺陷，随咬边深度的增加，咬边位置磁场信号减弱。

参考文献：

[1] 牛连山，王丛亮，董伟，等. 长输管道环焊缝缺陷返修[J].电焊机，2017，47（6）：55-58.

[2] 黄松岭. 油气管道缺陷漏磁内检测理论与应用[M]. 北京：机械工业出版社，2013.

[3] 杨理践，耿浩，高松巍. 长输油气管道漏磁内检测技术[J].仪器仪表学报，2016，37（8）：1736-1746.

[4] 戴光，吴忠义，朱祥军，等. 管道内外壁缺陷的漏磁检测[J]. 无损检测，2018，40（3）：19-23，28.

[5] 黄强，夏明明，范赵斌，等. 内检测技术在含油气水管道中的研究与应用[J]. 管道技术与设备，2019（5）：28-31.

[6] Yang L Y，Zhang S L，Gao S W. ANSYS simulation tech-nology of pipeline magnetic flux leakage inspection[J]. Ad-vanced Materials Research，2013（718-720）：1000-1005.

[7] 杨志军，陈德姝，陈亮，等. 腐蚀缺陷漏磁检测有限元模拟[J]. 无损检测，2015，37（11）：51-55.

[8] 苏林，成文峰，许志军，等. 油气管道缺陷漏磁检测有限元模拟[J]. 焊管，2020，43（4）：8-13，22.

[9] 鲁鑫. 油管漏磁检测的有限元分析及实验的研究[D]. 黑龙江：东北石油大学，2016.

[10] Sakai K，Morita K，Haga Y，et al. Automatic scanning sys-tem for back-side defect of steel structure using magnetic flux leakage method[J]. IEEE Transactions on Magnetics，2015，51（11）：1-3.

[11] 刘刚，陈雷，张国忠，等. 管道清管器技术发展现状[J]. 油气储运，2011，30（273）：646-651.

[12] 康宜华，陈艳婷，孙燕华. 超强磁化下漏磁检测的穿透深度[J]. 无损检测，2011（6）：27-29.

[13] 苏林，马雪莉，董凯. 长输管道盗孔检测技术分析[J]. 管道技术与设计，2020（3）：20-22.

[14] 宋小春，杨林，许正望. 管道周向磁化漏磁检测有限元分析[J]. 中国机械工程，2011（22）：2651-2653，2706.

[15] 苏林，成文峰，刘保余. 管道环焊缝缺陷漏磁检测信号仿真分析[J]. 焊接，2020（3）：10-16.