基于PSO的地铁运行多目标优化研究

袁浩轩

摘 要：为了降低城市轨道交通列车运行过程中的能耗，减少乘客旅行总时间，需要设置合理的时间调度表。从研究列车的发车间隔和停站时间入手，建立列车牵引计算模型和运行能耗和时间计算模型，得到单列车固定每个站间的运行“速度-位置”曲线，然后在满足运行速度、运行时间以及运行安全等约束条件下，通过多种群粒子群算法来优化计算发车间隔和各站停站时间。最后通过对广州七号线部分线路的MATLAB仿真模拟，证明了多种群粒子群算法在降低列车运行能耗和缩短运行总时间方面的有效性。

关键词：多种群粒子群算法;节能优化;再生制动

中图分类号：U231.92 文献标识码：A

0 引言

由于快捷方便、价格便宜、不易堵塞以及保护环境等诸多优点，轻轨地铁等城市轨道交通深得广大出行人们的喜爱，并且发展迅猛。因此，城市轨道交通已经成为了公共交通中极为重要的一部分，尤其在我国的一二线城市内，已经成为了人们出行必不可缺的工具之一。但是城市轨道交通系统的能耗大，如何在列车正常运行的前提下减少能耗并且缩短耗时成了一项难题。所以，在满足安全运行的条件下，对地铁节能和缩短耗时研究不仅方便了人们出行，也节约了能源降低了列车的运营成本，具有重要的研究意义。通过单列车的节能运行操纵策略，以减少能耗为目标，找到列车的控制操纵序列以及从一个工况到另一个工况的转换点，实现列车的优化运行[1]。

目前，有许多国内外学者对列车运行节能、安全以及耗时优化问题进行了研究，但大多只对单列车的节能进行了优化研究而未考虑到站运行总耗时，最终的优化调整可能并不实用以及忽略了多列车之间的再生制动的不足。因此，本文采用多种群粒子群算法，调整发车间隔及停站时间，增加相邻两车牵引与制动的重叠时间，增加再生利用率，从而达到减少列车运行的总能耗同时减少列车运行总时间的优化目标。最后，对广州地铁七号线部分线路进行多列车进行仿真分析，结论可为多列车运行节能和缩短耗时提供参考和指导。

1 多列车运行能耗和最终到站时间最优控制模型

列车在运行中主要视为单质点模型，当且仅当列车车身处于变坡道或变弯道处时将列车视为多质点处理;制动产生的再生制动能量优先被处于同一供电区间段加速列车吸收实验;上行线和下行线的供电系统不共享;忽略上下乘客所引起列车质量的变化，列车同质量，同车型，相同站间驾驶策略相同。

在列车的运行过程可表示如下[2-3]：

式中，为列车的基本阻力;为附加阻力，由线路中的坡道、曲线引起;、分别为列车的总质量和车长;、坡道千分数及坡道长度;、曲线半径及曲线长度。

由公式（1）、（2），结合最优控制理论，得到单列车的节能策略：列车启动阶段以最大加速度牵引，减少阻力做功;区间运行阶段尽量以惰性和滑行为主减少能耗;入站制动阶段，以最大制动能力制动减少能耗。

列车在制动过程中产生巨大的机械能，此时将电动机切换成发电机运转，进而将其转化为电能进行储存或利用[4]。城市轨道交通的站间距离小，牵引和制动十分频繁，若列车在制动持续时间段内，恰有相邻列车正在牵引，那么再生制动能量就可以供相邻列车直接使用进而减少储存能量转换消耗[5]。在客流高峰期时，发车间隔的缩短正好能大大地增加同一供电站内相邻列车加速与制动时间的重叠，因而本文主要针对客流高峰期，在发车密度较大的情况下对列车进行时刻表和能耗的多目标优化研究。既可以通过优化后发列车的发车间隔以及每个站点的停站时间进而获得较优的再生制动能源和最终到站耗时。

再生制动阶段的能量计算公式可表达为：

其中表示列车质量[6]，表示被回收利用的再生制动能量，和分别表示牵引与制动重叠时制动的加速度和初速度，表示重叠时间。

列车运行时间和能耗公式：

在满足运行安全性的前提下，结合最优控制理论，对后发列车能耗和总耗时进行求解，得到前沿解。多车能耗目标方程及优化的目标函数可表示为：

式中，表示列车停站时间，和分别为列车最小停站时间和最大停站时间;为列车在第个站间运行的计划用时;表示时间裕度，一般取值5%。

2 基于PSO模型求解

2.1 算法思想

直接采用PSO进行优化存在出现早熟现象、收敛性弱、最优解的精度低等缺点，因此本文对PSO进行如下改进：

一方面，对粒子群采用多种群协同分工策略，将整个粒子群分成3个小种群，分别负责时间，能耗以及均衡的寻优。另一方面，采用克隆算法针对每次迭代的优秀粒子进行深层挖掘，弥补对种群最优粒子以及全局最优粒子信息挖掘的缺漏。

因为改进后的粒子群采用的多种群协同分工策略，粒子速度和位置的迭代公式有所不同，标准粒子群主要受到种群最优粒子的引导，而本文所采用的方法对粒子的引导来自两方面：一方面是该粒子所在的小种群的最优粒子，另一方面则是外部档案选出相对应种群的优秀解。外部档案的解不单单来自于粒子群本身，还有克隆得出的优秀解，这也是本文要从外部档案选取优秀解来引导粒子飞行重要原因。由此粒子群迭代更新的公式如下：

式中，为粒子在第次迭代后速度;为粒子在第次的迭代位置;为惯性权重;，，为学习因子;，，是[0，1]的随机数;为个体历史最优值;表示第个小种群的最优粒子;为外部档案最优粒子。

模型求解步骤如下：

①粒子群的初始化：设置粒子群的总数N、迭代次数Gen、惯性权重等参数，将粒子群平均分成三个小种群;②挑选出可行解，计算每个可行解粒子的目标函数值 T 和 E，记录粒子的个体历史最优解以及各小种群的最优粒子;③使用网格法更新外部档案，并从中选取全局最优解;④根据公式（11）和（12）更新粒子群速度和位置;⑤计算更新后各粒子的目标函数值T和E;⑥克隆和，生成克隆群;⑦对克隆群进行变异操作;⑧保留变异后的可行解，計算克隆群变异后各粒子的目标函数值 T 和 E;⑨由 ⑤和 ⑧得到粒子的目标函数值 T 和 E，更新外部档案;⑩判断算法迭代是否结束，结束则输出 Pareto 解集，否则转至 ②。

3 仿真验证及实例分析

为了验证改进后的多种群粒子群算法在城市轨道交通的节能和缩短耗时的可行性和有效性，本文使用前述模型，结合“广州七号线”部分站点数据使用Matlab 2018a进行仿真实验。选取的线路为“大学城南站”-“石壁村”-“谢村” -“钟村”-“汉溪长隆”-“鹤庄”共六站，该段坡道曲线较多具有显著特征，所以选择该段作为仿真区间[7]。

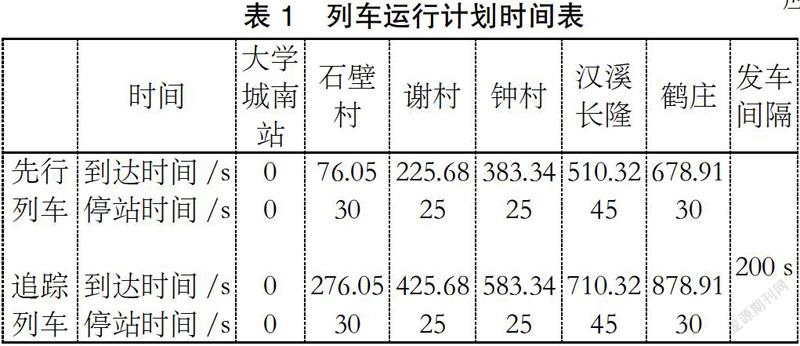
本文选取广州七号线部分线路的仿真时段为早高峰：7：00-8：00， 其原定发车间隔200s，中间站的停站时间[30 25 25 45]，列车运行计划时间表如表1所示：

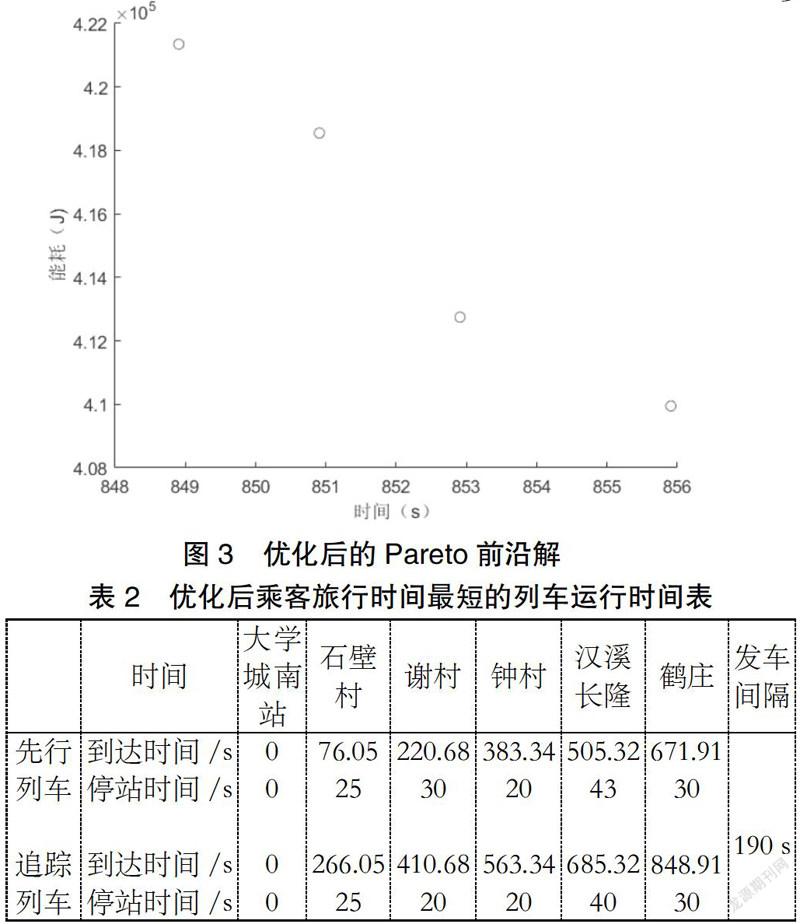
经Matlab仿真本文提出的算法后，得到满足约束条件的列车运行时间表的Pareto解集如图3所示。

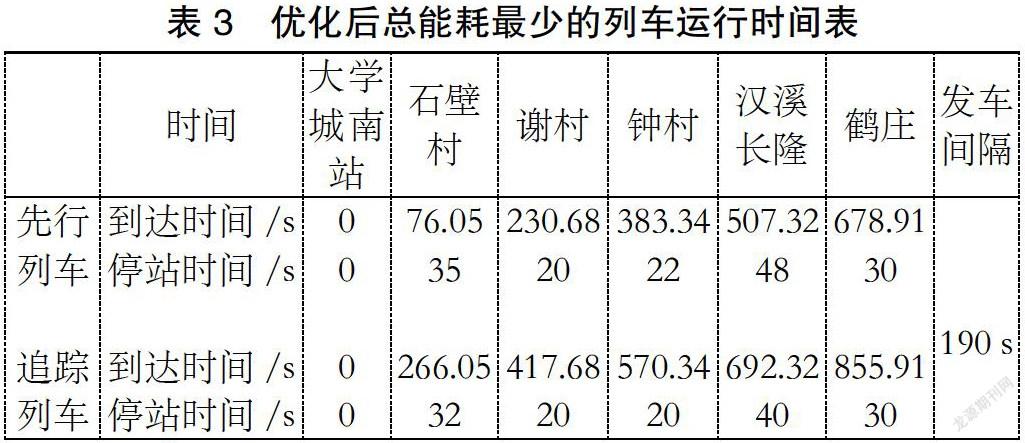
由表2可知，旅行时间最多减少了37 s，对应节能187.09 kW·h;由表3可知，最多节能198.49 kW·h，对应节时23 s。经优化算法得到的Pareto前沿解相比于原计划时间表在旅客乘车总时间和列车运行总能耗上都有明显的改善效果。

4 结论

（1）通过总结现有的列车节能驾驶策略的研究的空缺与不足，提出将多目标粒子群算法运用于列车驾驶策略研究。

（2）采用的PSO算法具有所需参数少、结构简单明快、程序操作简单等优点，但存在出现早熟现象、收敛性较弱、最优解的精度较低等缺点，对此本文提出了多种群粒子群的协同进化策略。

（3）以广州地铁七号线为例的仿真结果表明，该算法优化后的列车运行时间表使得乘客的旅行时间最多降低4.2%，列车运行总能耗最多降低32.6%。

参考文献：

[1]段玉琼，朱爱红，马晓娜，等.基于人工蜂群算法的高速列车运行节能优化研究[J/OL].铁道标准设计，2019，63（09）：163-168.

[2]韩龙涛.地铁列车牵引计算与仿真[D].北京化工大学，2014.

[3]杨彦强，刘海东，麻存瑞，等.列车节能运行目标速度控制优化研究[J].交通运输系统工程与信息，2019，19（01）：138-144.

[4]王斌，胡海涛，高仕斌，等.考虑再生制动时高速铁路牵引网潮流计算与分析[J].中国铁道科学，2014，35（01）：86-93.

[5]厉高，林建辉，庄哲，等.基于再生制动的城市轨道列车节能控制研究[J].铁道运输与经济，2019，41（03）：121-126.

[6]饶忠. 列车牵引计算[M]. 中国铁道出版社，1999.

[7]刘鑫榮.基于多目标的地铁列车运行节能技术研究与仿真[D].南京理工大学，2017.