充填挡墙压力变化规律模拟试验研究

宋宏元 周乐 刘龙琼 程文文

摘要：充填挡墙是将充填料浆封闭在采空区内实现预定功能的重要保障，研究充填挡墙在充填过程中的压力变化规律十分必要。从物理模拟试验入手，采用充填挡墙压力变化模拟试验装置，分析在充填过程中浓度、充填高度、脱水情况对充填挡墙压力变化的影响，并探究了快速充填与实际充填时充填挡墙压力差别。充填过程中尾砂浆体的脱水情况对充填挡墙压力变化影响较明显。模拟试验得到的规律与现场实测结果基本一致，可为矿山安全、经济地设计充填挡墙提供参考借鉴。

关键词：充填挡墙;压力变化;充填浓度;充填高度;脱水;模拟试验

中图分类号：TD862文献标志码：A开放科学（资源服务）标识码（OSID）：

文章编号：1001-1277（2020）05-0040-06doi：10.11792/hj20200508

井下采空区的封闭是实施充填的必要条件之一，作为充填采空区封堵物的充填挡墙也就应运而生。充填挡墙是充填采矿法的有机组成部分，可将充填料浆封闭在采空区内，是充填料浆在采空区内实现预定功能的重要保障[1]。由于充填物料的多样性、采空区水文地质条件的复杂性、充填挡墙选择的多样性，大多数矿山往往采用工程类比法和经验法来设置充填挡墙，缺乏对充填过程中充填挡墙压力变化规律的了解，导致充填挡墙的强度设计过高或过低，从而造成不必要的资源浪费或采场事故[2]。因此，本文以中国黄金集团江西金山矿业有限公司（下称“金山金矿”）尾砂充填挡墙设计为背景，重点研究充填过程中充填挡墙压力变化规律，对安全、经济地设计充填挡墙具有借鉴意义。

1 充填挡墙压力变化模拟试验

1.1 试验装置

充填挡墙压力变化模拟试验装置由模拟空区、模拟挡墙、测试装置3部分组成（见图1）。其中，模拟挡墙由2部分组成：一是隔离尾砂浆体的柔性薄膜;二是紧贴塑料薄膜用来传递充填挡墙压力的有机玻璃棒，二者接触面光滑，阻力较小。

该试验装置可测得整个充填过程中充填挡墙压力的持续变化规律。由于在充填挡墙压力测试的过程中存在一定的阻力，主要为传递压力的有机玻璃棒与有机玻璃管壁摩擦产生的摩擦阻力，因此需要对试验装置进行校核。校核后的结果见表1。

充填挡墙承压力的计算公式[3]为：

F=ρghA（1）

式中：F为充填挡墙承压力（N）;ρ为水密度（kg/m3）;h为水面高度（m）;A为挡墙面积（m2）。

经计算：F=9.42 N，修正系數μ=8.25/9.42=0.875。

1.2 试验过程

利用自制的充填挡墙压力变化模拟试验装置进行充填挡墙压力测量，试验过程可分为以下几步：①固定试验装置，拧动螺栓使推拉力计推动有机玻璃棒紧贴

塑料薄膜，此时推拉力计有0～0.50 N的示数;②计算称量所需的尾砂、水;③将尾砂、水倒入搅拌机搅拌10 min;④将搅拌均匀的尾砂浆体快速充入有机玻璃管至指定高度，记录推拉力计示数;⑤每隔一定时间记录数据，间隔时间2～30 min，前期时间间隔短，后期视情况延长;⑥待示数不变（间隔1 h示数无变化），进行下一次充填，重复①—⑤。充填挡墙压力测试现场见图2。

2 首次充填挡墙压力分析

尾砂浆体充入试验装置之后，根据尾砂浆体的形态变化，将其分为3个阶段：液体阶段、过渡阶段、无黏性散体阶段[4]。

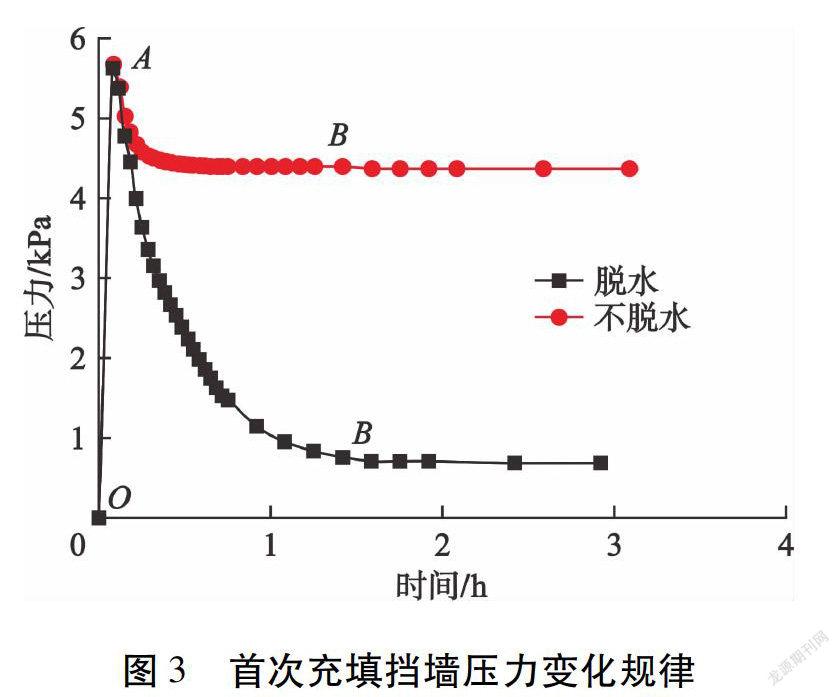
采用快速充填方式得到的首次充填挡墙压力随时间的变化规律见图3。OA段为快速充填过程中充填挡墙压力变化曲线，A点是充填完成点。A点之后是充填完成后充填挡墙压力变化曲线。结合充填形态的变化规律及充填挡墙压力的变化规律，将OA段视为液体阶段，AB段为过渡阶段，B点之后为无黏性散体阶段[5]。从图3可以看出：脱水和不脱水2种条件下，首次充填挡墙压力变化规律基本相似，但是脱水条件下充填挡墙压力只有不脱水条件下的20 %左右。

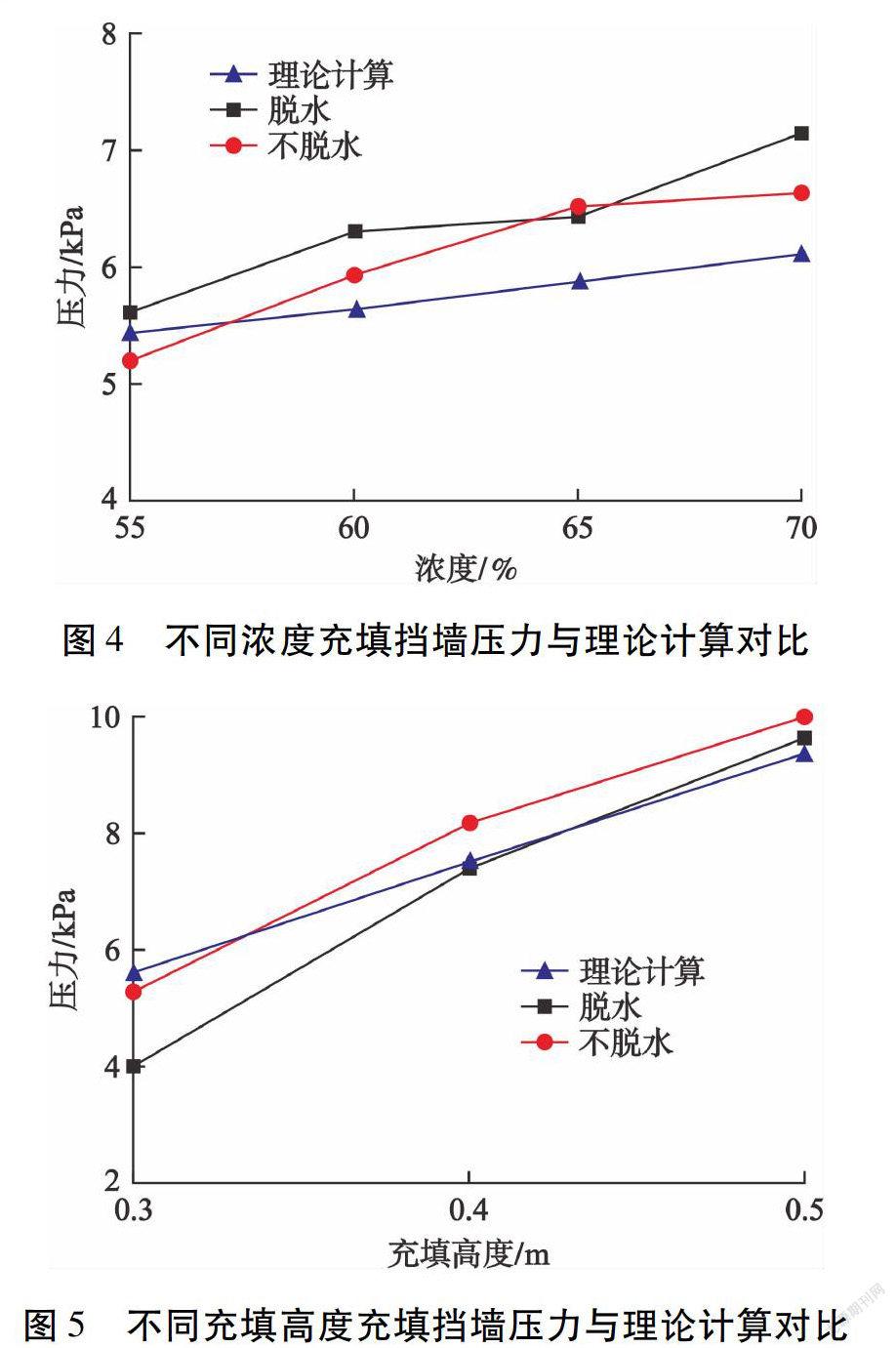
1）液体阶段。充填挡墙压力实测数据与按照静水压力理论计算得到的结果比较见图4、图5。不同浓度下首次充填挡墙压力与理论计算结果对比见图4。 从图4可以看出：浓度越高，充填挡墙压力越大;这是由于浓度高，尾砂浆体的密度大，导致充填挡墙压力大。不同充填高度下首次充填挡墙压力与理论计算结果对比见图5。从图5可以看出，在液体阶段充填挡墙压力随充填高度的增加呈线性增加的趋势。

2）过渡阶段。从图3可以看出：AB段充填挡墙压力不断减小，并且减小的速率并非恒定，前期压力下降较快，后期压力变化趋于平缓。充填挡墙压力减小主要是由于尾砂的沉降、脱水，而且散体状态下的内摩擦角和内聚力都不再为0，充填挡墙的压力比液体状态下小很多。对AB段的数据进行拟合，结果如下：p=1.22t-0.76（脱水）（2）

p=4.41t-0.05（不脱水）（3）

式中：p为充填挡墙压力（kPa）;t为时间（h）。

式（2）、式（3）基本结构是一致的，可以将其归纳为：

p=atb（a>0，t>0，b<0）（4）

该函数在给定区间内单调递减，曲线斜率为负值，且斜率不断增大。

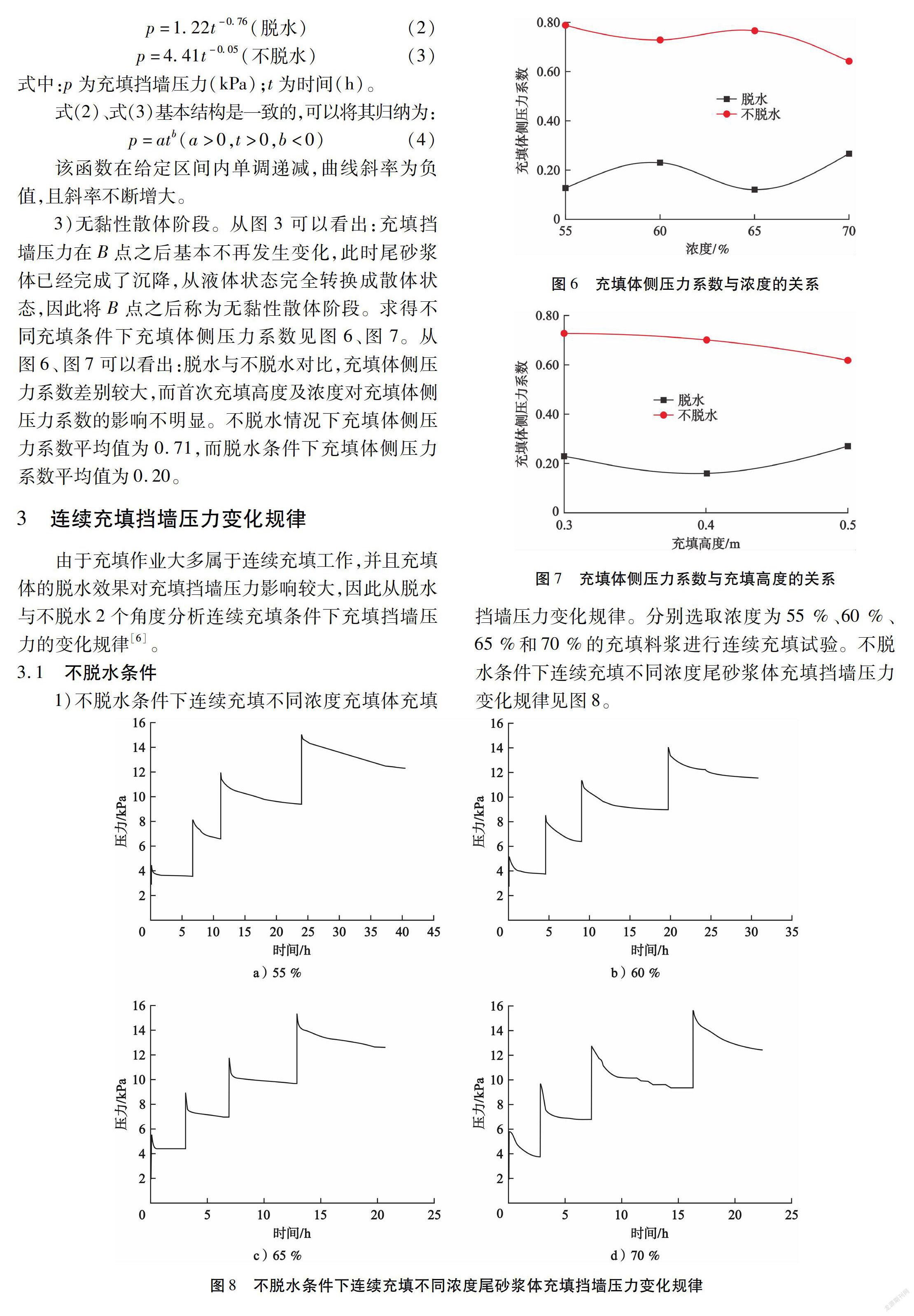
3）无黏性散体阶段。从图3可以看出：充填挡墙压力在B点之后基本不再发生变化，此时尾砂浆体已经完成了沉降，从液体状态完全转换成散体状态，因此将B点之后称为无黏性散体阶段。求得不同充填条件下充填体侧压力系数见图6、图7。从图6、图7可以看出：脱水与不脱水对比，充填体侧压力系数差别较大，而首次充填高度及浓度对充填体侧压力系数的影响不明显。不脱水情况下充填体侧压力系数平均值为0.71，而脱水条件下充填体侧压力系数平均值为0.20。

3 连续充填挡墙压力变化规律

由于充填作业大多属于连续充填工作，并且充填体的脱水效果对充填挡墙压力影响较大，因此从脱水与不脱水2个角度分析连续充填条件下充填挡墙压力的变化规律[6]。

3.1 不脱水条件

1）不脱水条件下连续充填不同浓度充填体充填

挡墙压力变化规律。分别选取浓度为55 %、60 %、65 %和70 %的充填料浆进行连续充填试验。不脱水条件下连续充填不同浓度尾砂浆体充填挡墙压力变化规律见图8。

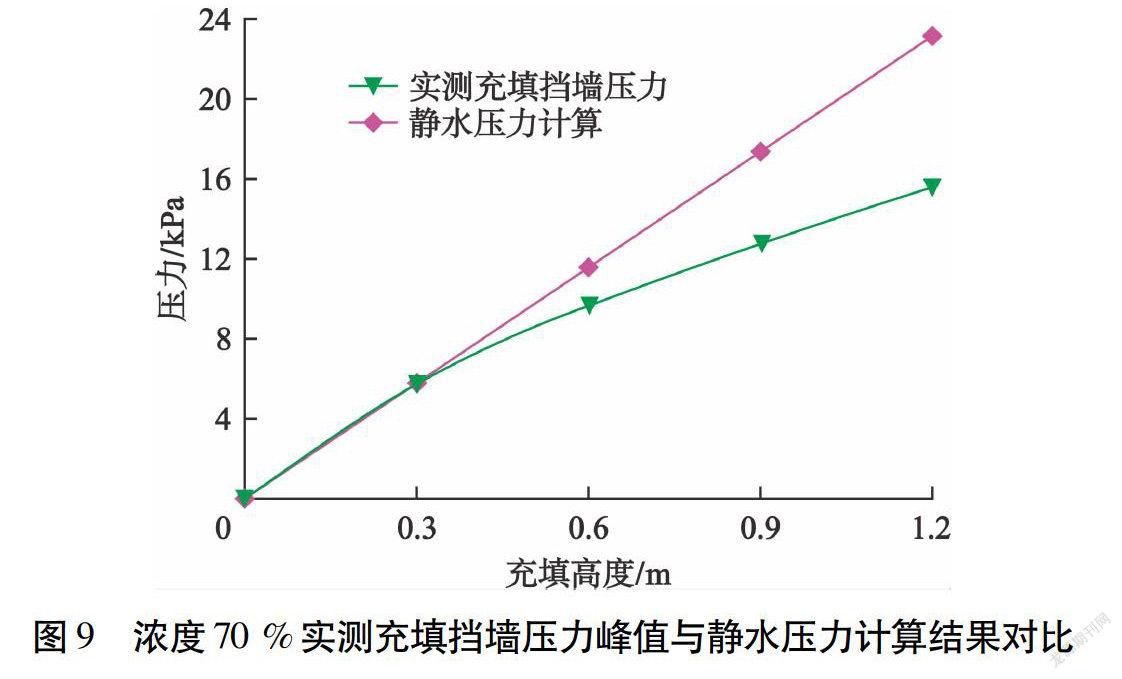
从图8可以看出：连续充填条件下，每次尾砂浆体充入采空区时充填挡墙压力都会快速增大，当充填完成后充填挡墙压力逐渐减小，这与首次充入尾砂浆体充填挡墙压力变化规律基本一致。取每次充填完成时的充填挡墙压力峰值进行对比，可以发现：浓度越高，充填挡墙压力越大，但浓度的影响较小，充填高度为1.2 m时，浓度70 %的充填挡墙压力仅比浓度55 %的高4.7 %。选取浓度70 %的充填挡墙压力峰值与静水压力计算结果作对比，结果见图9。

从图9可以看出：充填挡墙压力并非按照静水压力计算的结果呈线性增长，而且充填高度越高，其与静水压力计算结果的差距越大;说明采用静水压力计算充填挡墙压力的不合理性。这是因为：一是随着充填高度的增加，位于底部的充填物料不断被压实，导致充填挡墙的侧压力系数增加;二是随着充填高度的增加，上部荷载不断增加，充填挡墙与采空区壁的相互作用力也逐渐增加，从而使得采空区壁对充填物料的摩擦力增加[7]。

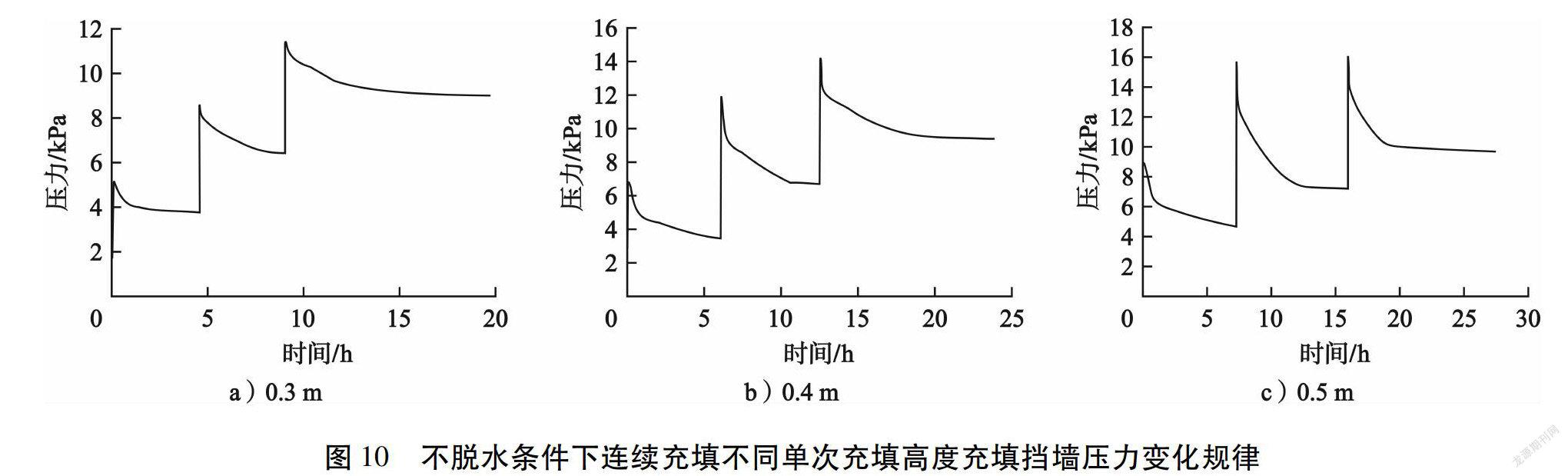
2）不脱水条件下连续充填不同单次充填高度充填挡墙压力变化规律。在相同浓度的充填料浆下，分别选取不同单次充填高度0.3 m、0.4 m、0.5 m进行连续充填试验。不脱水条件下连续充填相同浓度不同单次充填高度充填挡墙压力测定结果见图10。

从图10可以看出：不同单次充填高度下充填挡墙压力的变化规律与之前不同浓度下基本一致。就单次充填高度来说，单次充填高度越高，充填挡墙受力越大[8]。

3.2 脱水条件

1）脱水条件下连续充填不同浓度充填挡墙压力变化规律。在实际尾砂充填中，矿山一般都会尽量完善脱水设施，包括敷设脱水管、在充填挡墙上敷设滤水管等，目的是让充填料浆中的水尽快脱出，提高充填效率。因此，需模拟自由水基本都脱出条件下，连续充填时充填挡墙压力的变化规律。为了更清晰地分析脱水情况对充填挡墙压力的影响，取同一浓度，单次充填高度0.3 m并连续充填条件下脱水与不脱水的充填挡墙压力峰值进行对比，结果见图11，其中充填过程中脱水的模拟通过充填挡墙压力变化模拟试验装置底板的脱水孔来实现。

从图11可以看出：脱水条件下充填挡墙压力与不脱水条件下相比，不仅充填挡墙压力的变化规律不一样，而且脱水条件下充填挡墙压力比不脱水条件下小很多，充填高度为1.2 m时，脱水条件下充填挡墙压力平均只有不脱水条件下的24.3 %。因此，在脱水效果较好的充填采空区，随着充填高度的增加，充填挡墙压力会远远小于脱水效果较差的充填采空区，这样可以极大地降低充填挡墙发生事故的概率。

2）脱水条件下连续充填不同高度充填挡墙压力变化规律（见图12）。从图12可以看出，不同充填高度下充填挡墙压力的变化规律基本一致。脱水条件下仍是单次充填高度越高，充填挡墙压力越大。

通过对脱水情况的分析发现：脱水对充填挡墙压力有着十分重要的影响，脱水效果好的充填挡墙压力要远远小于不脱水条件下的充填挡墙压力。

4 实际充填挡墙压力变化规律

由于实际充填不可能在几分钟内完成，因此有必要对实际充填条件下充填挡墙压力变化规律进行探究。本文通过降低充填速度来实现模拟实际充填条件，设计浓度60 %，充填高度1.0 m，充填时间1 h，不脱水，匀速充填。试验结果见图13。

从图13可以看出：模拟实际充填挡墙压力变化规律与前述部分基本一致，但也有区别。由于采用匀速充填，充填时间与充填高度呈正比，随着充填时间的增加，即充填高度的增加，充填挡墙受力并非线性增加。对峰值点前的充填挡墙压力数据进行多项式拟合，结果见式（5）。

p=-4.42t2+20.53t-0.04（5）

峰值点后的充填挡墙压力变化规律与前文一致，峰值点的充填挡墙压力为静水压力计算结果的77 %。因此，可以推测实际充填过程中，首次充填挡墙压力峰值比静水压力计算的峰值要小。

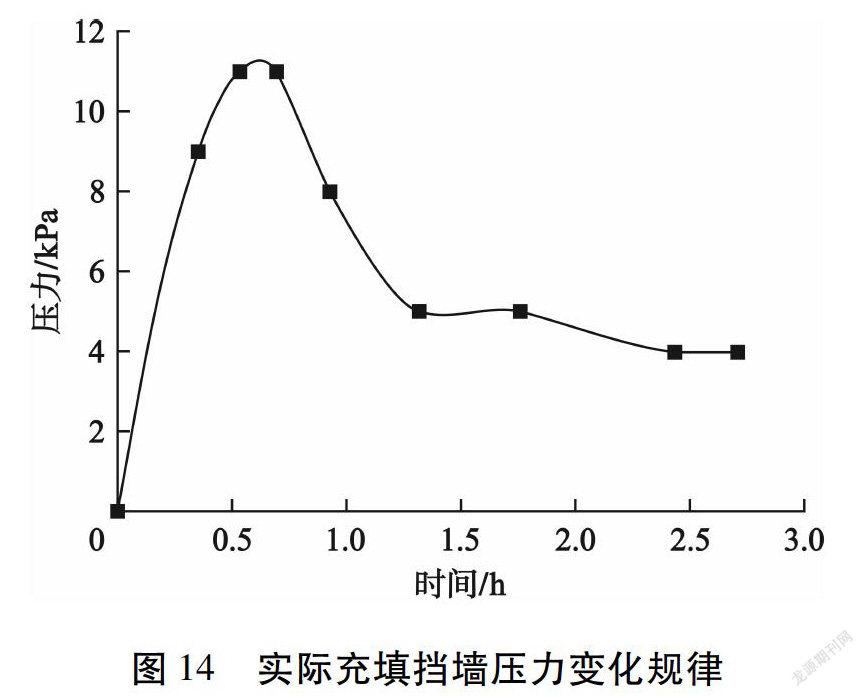
为了验证模拟试验的准确性，对井下充填挡墙的压力变化进行监测，测得的实际充填挡墙压力变化规律见图14。现场实测的充填挡墙压力变化规律与模拟试验得到的变化规律（见图13）基本一致。

实际充填中充填挡墻压力峰值与静水压力计算结果差距较大，主要是因为充填过程中，充填与沉降同步进行。当尾砂浆体充入到采空区后，尾砂浆体就已经开始发生沉降;当单次充填完成时，尾砂浆体下部有一部分已经沉降。充填完成时充填挡墙实际压力与静水压力计算结果的差异受多方面因素影响，包括采空区形状、充填速度、浓度、脱水情况等。因此，采用快速充填方式得到的充填挡墙压力值要高于实际充填挡墙压力。

5 结 论

1）尾砂浆体首次充入模拟采空区的过程中，液体阶段充填挡墙压力最大，随着尾砂浆体的沉降、脱水和压实，充填挡墙压力逐渐减小。在液体阶段可以采用静水压力法进行计算，但是在尾砂沉降完成之后，不适宜采用静水压力法计算。

2）连续充填时，不脱水条件下充填挡墙压力峰值变化规律与开口向下的抛物线前半段相似;脱水良好条件下对充填挡墙压力峰值前期有增大趋势，后期逐渐减小，且同等条件下不脱水充填挡墙压力要高于脱水充填挡墙压力。

3）在充填挡墙压力的影响因素中，尾砂浆体的脱水情况对充填挡墙压力变化规律影响较明显。由于充填采空区的充填体脱水情况难以评估，因此选择完全不脱水条件下充填挡墙压力进行研究具有代表意义。

4）在模拟实际充填条件下充填挡墙压力变化规律时可以发现，单次充填时，充填挡墙压力并非与时间或者充填高度呈线性增加的关系。充填完成时，充填挡墙压力峰值与按照静水压力计算的结果有差距，二者相差23 %。

[参 考 文 献]

[1] 程海勇，吴爱祥，罗淦华，等.轻型充填挡墙力学分析与构筑工艺[J].金属矿山，2016（9）：58-61.

[2] 徐钊.充填采矿法挡墙受力分析及安全性研究[J].铜业工程，2018（4）：11-13.

[3] 袁世倫.盘区大孔采矿采场全尾砂充填挡墙力学特性研究[J].中国矿山工程，2011，40（4）：9-12.

[4] 李广涛，乔登攀.大空区嗣后尾砂充填挡墙强度模型与应用[J].有色金属工程，2017，7（3）：88-92.

[5] 曹宗权.充填挡墙影响因素分析与应用[J].采矿技术，2015，15（3）：35-37.

[6] 黄建君.充填法挡墙强度模型研究及应用[D].昆明：昆明理工大学，2014.

[7] 薛奕忠.高大型采场全尾砂充填挡墙可靠性的力学分析[J].江西理工大学学报，2008，29（5）：18-22.

[8] 杨玉学.河北某铁矿充填挡墙快速砌筑工艺[J].金属矿山，2016（8）：152-154.

Abstract：Filling retaining wall is important guarantee to seal the filling slurry in the goaf to achieve the predetermined function.It is essential to study pressure variation rules of the filling retaining wall in the filling process.The paper starts with the physical simulation test and uses the filling retaining wall pressure test device to analyze the influence of filling density，filling height and dehydration on the pressure variation of filling the retaining wall during the filling process，and explore the pressure difference between the rapid filling and the actual filling.The dehydration of tailings slurry in the filling process has greater influence on the pressure variation of the retaining wall.The rules obtained from the simulation test results are consistent with the field test results，and can provide reference for the safe and economic design of the retaining wall.

Keywords：filling retaining wall;pressure variation;filling density;filling height;dehydration;simulation test