基于质点成形运动和端面型线的EPS蜗杆球面螺旋面模型构建

王少英

摘要：本文研究了汽车电子助力转向（EPS）减速器中蜗杆球面螺旋线的成型原理，并且对球面螺旋线按照质点成型运动原理进行数学建模。根据螺旋曲面的形成原理，构建基于端面型线的新的球面螺旋面模型;研究了球面螺旋线和球面螺旋面的特征参数;运用MATLAB编程通过数值计算和函数可视化功能，得到球面螺旋线。

关键词：球面螺旋面;成型原理;MATLAB编程;端面型线;模型

0  引言

EPS（汽车电子助力转向）中的减速器主要起降低速度和增加转矩的作用，因此常用蜗轮蜗杆减速器。现在常用的涡轮蜗杆机构主要有效率低、摩擦因数较高、润滑效果不好，热量大等缺点。而利用球面螺旋面做蜗杆螺旋面可以提高传动效率，使结构紧凑、动作灵活，降低摩擦。EPS中蜗杆的球面螺旋面模型如何构建是这种新型蜗杆球面螺旋面的关键技术。

螺旋曲面的种类有许多种，对不同的螺旋曲面其成形原理和数学建模都有区别，对螺旋曲面统一的成形原理和模型的构建缺少系统研究，对特殊类的螺旋曲面比较复杂的球面螺旋面对其运动的成形原理和数学模型的研究也鲜有报道。为此，通过对螺旋曲线和曲面的成形原理以及数学模型的构建入手，引出球面螺旋面的成形运动原理與模型的构建。

1  球面螺旋线的成形原理

球面螺旋线的成形运动为质点在两个圆周运动的组合下按照一定的运动规律形成的，即为第三类（CC）螺旋曲线。

球面螺旋线的成形特征是有两个圆周运动合成的运动形式，是一种光滑的螺旋曲线，它的形成是由质点在动坐标系中绕原点以某一参数作圆周运动，并同时动坐标系又在定坐标系中绕一轴以某一参数作圆周运动。如图1所示。

2  基于质点成形运动的球面螺旋线数学模型建立

根据球面螺旋线的成形原理，通过给定相应的参数就可以得到球面螺旋线的数学方程。两个圆周运动合成的球面螺旋面：规定初始位置动坐标系与定坐标系的Y轴重合，动系相对于定系绕Y轴转过λ角度，母线绕着动坐标系Y轴，以参数等于β0做圆周运动，动系绕定系X轴做参数为α0的圆周运动。

根据运动成形原理，可以得到在欧式空间内的转换矩阵：

取质点的初始坐标为（0，r，0）得到球面螺旋线的方程：

球面螺旋线的特征是复杂的，在成形过程中为了降低球面螺旋线的复杂度，在构造球面螺旋线时保持一般螺旋线的特征有利于对球面螺旋线的研究，其中一个重要参数就是螺旋角，螺旋角的恒定是螺旋曲线中的一个重要特征，为保持球面螺旋线的螺旋角是一个定值即为等螺旋角的球面螺旋线，因此，此螺旋线的方程满足：

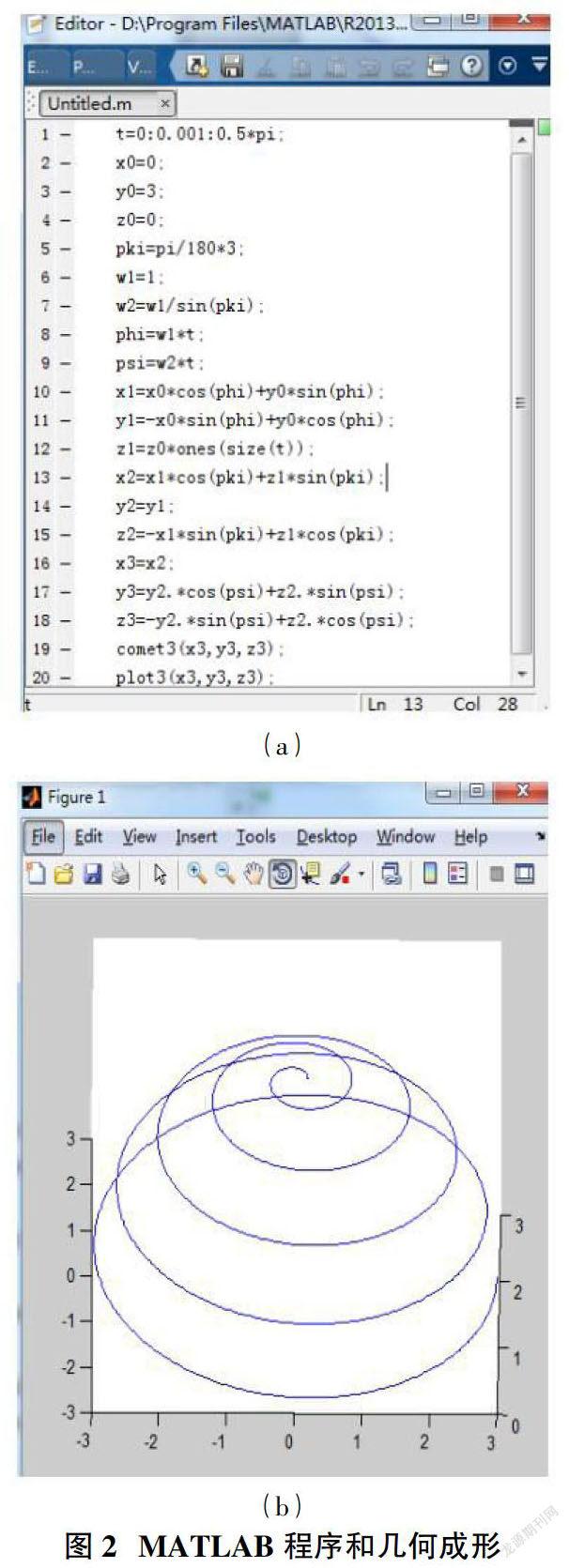
依据对球面螺旋线的定义和成形原理结合以及前面的数学模型运用MATLAB编程通过数值计算和函数可视化功能，得到如图2所示的球面螺旋线，其中图2（a）为编程代码，图2（b）为球面螺旋线的成形。

3  基于端面型线沿球面螺旋线运动的球面螺旋面数学模型

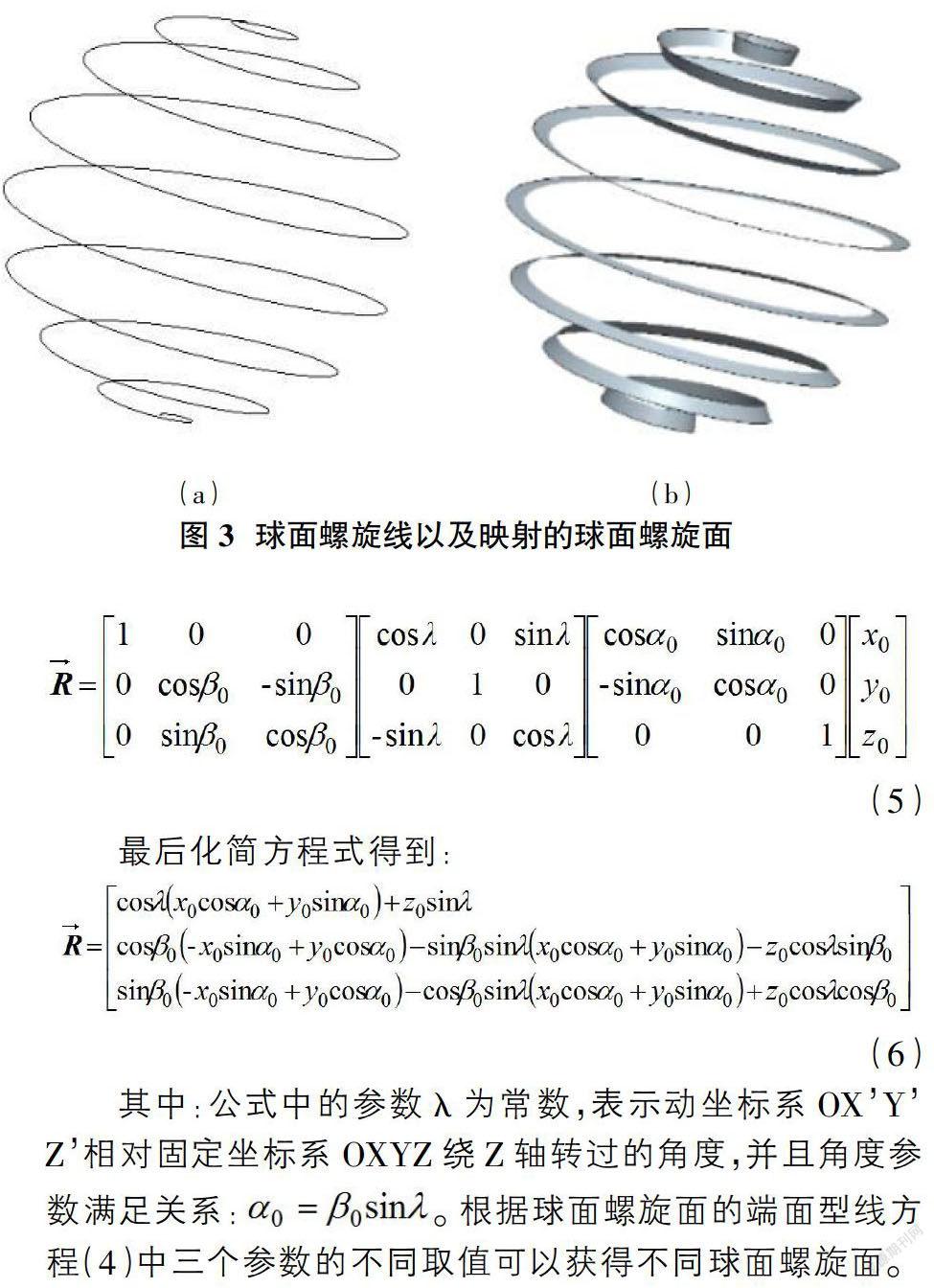
质点和直线（或曲线）的成形运动分别是球面螺旋线与球面螺旋面的成形原理。若想获得球面螺旋面方程的数学模型，只需将端面为质点的球面螺旋线替换成端面为直线（曲线）的端面形线，以原球面螺旋线为轨迹的端面形线，运动成形为球面螺旋面。如图3所示，其中图3（a）为球面螺旋线，图3（b）为球面螺旋面。

取球面螺旋面的端面型线通用数学方程为：

依据球面螺旋面的成形原理，将球面螺旋面端面型线的方程（4）联合空间矩阵转换方程（1）得到球面螺旋面的数学方程式为：

最后化简方程式得到：

其中：公式中的参数λ为常数，表示动坐标系OX’Y’Z’相对固定坐标系OXYZ绕Z轴转过的角度，并且角度参数满足关系：■。根据球面螺旋面的端面型线方程（4）中三个参数的不同取值可以获得不同球面螺旋面。

4  小结

利用球面螺旋面做蜗杆螺旋面可以提高传动效率，降低摩擦，因此主要分析研究了EPS（汽车电子助力转向）中球面螺旋面蜗杆的新型螺旋面模型构建。文章首先根据螺旋曲线的基于质点成形原理研究螺旋曲面的成形与端面型线的关系，再根据曲面成形原理得到螺旋曲面的成形原理和分类，并分别给出了螺旋面的数学方程。

最后，根据对螺旋曲线的成形运动特点，直线运动与圆周运动的组合形式变换得到了球面螺旋线和球面螺旋面的成形运动特点，根据球面螺旋线的成形运动形式，构建了球面螺旋线的模型，根据球面螺旋面的成形运动原理构建了球面螺旋面的模型。

参考文献：

[1]杨斌，张茂，等.Pro/E 在复杂曲面造型设计中的应用[J].机电产品开发与创新，2004（4）：57-58.

[2]Li Z， Liu Q. Surface topography and roughness in hole-making by helical milling[J]. The International Journal of Advanced Manufacturing Technology， 2013， 66（9-12）： 1415-1425.

[3]Kang S K， Ehmann K F， Lin C. A CAD approach to helical groove machining— I.mathematical model and model solution[J]. International Journal of Machine Tools and Manufacture， 1996， 36（1）： 141-153.

[4]Manfredo P. do Carmo. Differential Geometry of Curves and Surfaces[M].China Machine Press， 2004， 3.

[5]李蕾，冯显英，张成梁，等.滚珠型弧面凸轮分度机构动力学模型建立及模态分析[J].振动与冲击，2012，31（16）：62-65.