基于趋势二次移动平均法的新冠肺炎疫情的建模和预测

段班祥 吴兆鑫 蔡丹敏 许梓炫

摘 要：文章探讨新型冠状病毒国家管控问题。查找新型冠状病毒实时数据，并提取2019年GDP排行前十的国家的数据。对世界各主要国家的数据进行数据标准化后，对数据进行了主成分分析，构建了主成分的方差贡献率模型。运用趋势二次移动平均法，构建了世界主要国家的发展趋势预测模型，得出了2019年GDP排名全球靠前的国家在疫情期间的管控能力，分析了各国政府防控措施手段的有效程度。

关键词：新型冠状病毒;趋势二次移动平均法;主成分分析;疫情预测

中图分类号：F224 文献标识码：A 文章编号：1674-1064（2020）08-0001-04

新型冠状病毒肺炎是近百年来人类遭遇的影响范围最广的全球性大流行病，对全世界是一次严重危机和严峻考验。人类生命安全和健康面临重大威胁。由于各个国家本身的经济能力、政治体制、文化差异、各国人民对疫情重视程度的差异及各国医疗水平等因素，导致每个国家抗击疫情的道路各不相同。为此，搜集各国疫情数据，进行大数据分析，建立数学模型，最终得到新冠病毒疫情发展的基本特点和规律，是文章研究的主要目的。

1 研究思路和方法

为评价各主要国家管控新冠疫情的效果，笔者选取了疫情发展最为严重且全球GDP排行靠前的国家，通过网站“http：//hao.199it.com/ncov.html”爬取世界主要国家的疫情数据，然后对数据进行标准化等预处理，利用主成分分析构建方差贡献率，求出方差贡献率[1]累计占比超过95%的第一、第二主成分，根据各指标数据与主成分相关性得出国家的综合得分，最终获取各主要国家的管控效果。

为建立主要国家疫情发展趋势的模型并进行预测，笔者根据时间序列模型的二次移动平均法[2]，改进后采用趋势移动平均法，得到了各主要国家疫情发展的趋势预测模型[3]，最后在相关软件推演中得到推导和实证。

2 世界主要国家疫情发展特点

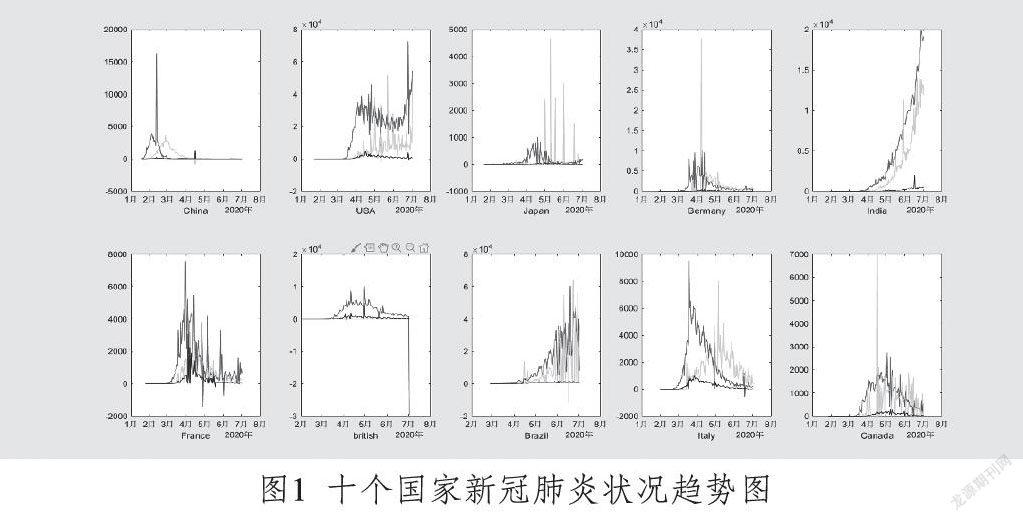
笔者在matlab中对世界GDP靠前的十个国家的数据进行处理并绘制成趋势图，新增确诊、新增治愈、新增死亡的趋势变化如图1所示。

其中，红色曲线为新增确诊，绿色曲线为新增治愈，黑色曲线为新增死亡。其中，部分出现负值的原因为人为更改统计方式导致的，因此将出现负值的数据一并处理为0，这对结果并不会有很大的影响。根据图1，可将十个国家各自的疫情程度进行分类。其中，USA（美国）、India（印度）、Brazil（巴西）这三个国家新增确诊人数都大致呈现线性上升的趋势，说明疫情程度在一直恶化;而其他国家都大致呈先上升后下降再趋向于平稳的趋势，说明疫情程度得到有效地控制。根据图表分析，可以粗略地分为两类：USA（美国）、India（印度）、Brazil（巴西）这三个国家为一类;其他国家为一类。

将这十个国家的新增确诊、新增治愈、新增死亡数据进行汇总后求平均值，且计算出累计的确诊人數，如图2所示。并用Q型聚类法[4]中的欧氏距离计算出各个国家之间的距离，如图3所示。

根据图3的聚类分析图可得出最终的分类结论：印度、美国、巴西各为一类;剩余国家为一类。

3 世界主要国家疫情综合评价模型

将GDP排名前十的国家在疫情期间的各数据指标取平均值，得到如图4所示的指标平均数据。

通过计算得出了主成分的方差贡献率，并对方差贡献率进行可视化，如图5所示。

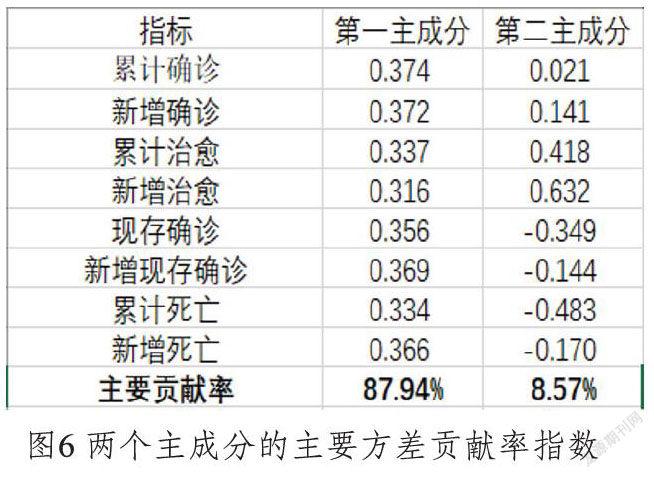
通过计算得出，前两个主成分的方差贡献率累计已达到96.5%。其中，第一主成分的主要方差贡献率为87.94%，第二主成分的主要方差贡献率为8.57%。由于前两个主成分分析占比超过95%，则考虑国家管控效果时，可只考虑前两个主成分分析[5]。图6为第一主成分和第二主成分各自主要方差贡献率的各个指数。

根据以上数据，利用主成分综合评价模型求得：

可得出最终的综合得分计算公式：

根据各个指数与两个主成分分析的相关性可发现，综合得分越低，则代表该国家对疫情的管控效果越强。世界主要国家的综合得分由低到高排序如表1所示。

因此可得出，在世界主要国家当中，日本、加拿大、中国是疫情期间管控效果最好的;而印度、巴西、美国是疫情期间管控效果最差的。

4 基于趋势二次移动平均法的新冠肺炎疫情的数学模型

二次移动平均法，是对一次移动平均数再进行第二次移动平均，再以一次移动平均值和二次移动平均值为基础建立预测模型[2]，计算预测值的方法。使用一次移动平均法的平均数计算公式为：

然后再对一次移动平均的数据进行第二次移动平均，即二次移动平均的计算公式为：

其次利用移动平均的滞后偏差来建立趋势预测模型，因此设趋势模型为：

其中，t为当前时间数;T为由t至预测期的时间数;at为截距;bt为斜率。两者又称为平滑系数。

然后根据移动平均值来确定平滑系数：

所以：

因此：

根据以上公式推导可得出：

综上可得，平滑系数的计算公式为：

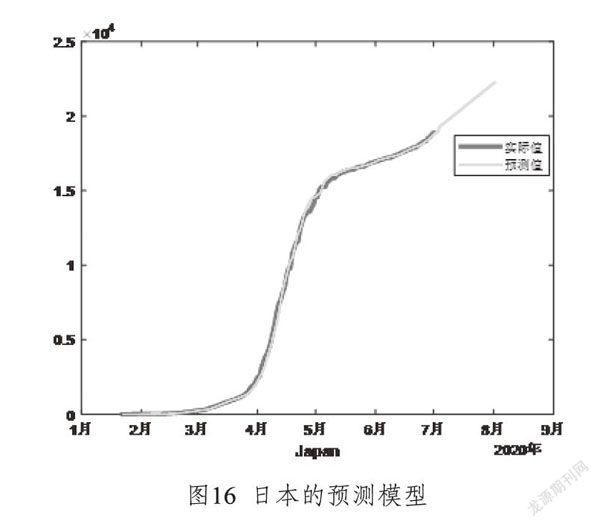
根据以上二次移动平均法对新冠疫情进行了预测，得出世界各主要国家新冠疫情的发展趋势预测模型，如图7至图16所示。

通过计算与模型观察可以得出各国的相对平均误差，如表2所示。设相对平均误差为f，预测值为yhat，根据相对平均误差，对预测值进行以下处理，使预测值更加接近实际值。

5 结语

文章运用了趋势二次移动平均法，构建了世界主要国家的发展趋势预测模型，很好地对世界各国的疫情及抗疫成效进行了分类评价及预测。在建模的过程中，坚持从数据本身出发寻找合适的模型，从而保证模型与数据之间具有较好的拟合效果，为后续的统计分析提供了便利，也保证了模型的可靠性。

参考文献

[1] 卓金武，王鸿钧.MATLAB数学建模方法与实践（第3版）[M].北京：北京航空航天大学出版社，2018.

[2] 白晓东.应用时间序列分析[M].北京：清华大学出版社，2017.

[3] 范晋蓉，白晓东，郭佩汶，等.广西壮族自治区病毒性肝炎发病数的建模与预测分析[J].检验检疫学刊，2019，29（6）：1-5.

[4] 胡雷芳.五种常用系统聚类分析方法及其比较[J].浙江统计，2007（4）：11-13.

[5] 马知恩.传染病动力学的数学建模与研究[M].北京：北京科学出版社，2004.