基于承载力分配法的多功能重载AGV结构优化
蒋君侠,张圣麟,朱伟东
(浙江大学 机械工程学院,浙江 杭州 310027)
0 引言
近年来,随着我国对飞机数字化装配技术研究投入力度的加大,一系列航空制造高端装备和总装配脉动生产线的软硬件系统陆续被研制出来,大大提高了飞机装配的质量和效率,也为我国航空制造业的转型升级奠定了技术基础[1-2]。作为智能工厂高效运作的关键环节之一,柔性化与智能化的物料配送技术已经成为飞机装配生产线未来的研发重点之一。目前,虽然大部分零件和组件可以用普通的自动导引车(Automated Guided Vehicle, AGV)完成运输调度[3-4],但是对于机身、机翼这类尺寸和重量极大的部件来说,其转运仍然需要借助人工操纵吊车,严重降低了生产线的整体效率并增加了工人的劳动量。另一方面,这些大部件的成品件、管路和线缆等往往需要手工安装,而这一工序目前只能在固定工装托架上完成,大大降低了生产线的柔性。为了解决上述问题,有必要研发一种大尺寸、重载的、全向移动同时具备智能支撑功能的AGV。
在飞机装配车间复杂的路况下,AGV需要承载着几十吨大部件完成较多的直线和转弯运动,对其结构设计的合理性和可靠性要求很高,如何在合理分配各个支撑点承载力的基础上完成车体结构的轻量化设计是本文待解决的问题。国外针对重载AGV的研究与应用起步较早,美国Wheelift公司[5]研制的AGV采用4个车轮模块的Uniload液压悬挂系统对承载力进行跟随调整以适应不平路面;德国KUKA公司[6]研制的OmniMove移动平台采用安装在车体两侧的电动或液压升降单元来承载大部件,并通过增加升降单元的安装数量来承载超长部件;VALE等[7]针对一种用于核聚变设施维护的重载AGV,分析对比了多种导航算法对车体轮系设计和运动稳定性的影响。然而,这些研究成果均未考虑重载AGV承载力对其车体结构设计的影响。国内针对重载AGV结构设计的研究较为丰富,卢敬铭[8]设计的重载仓储AGV底盘可以实时监控驱动轮和辅助轮负载,但是并未将其用于车体结构优化;金鹏[9]基于承载梁的支撑力和弯曲力矩约束方程,采用遗传算法开展重载AGV尺寸优化设计,但是该理论只适用于小尺寸简单结构;吴宁强等[10]基于汽车生产线重载AGV框架举升和三轮着地的极限工况,对AGV的框架进行了拓扑优化和等效应力分析,但未给出一种广泛适用的承载力分配理论。
本文针对飞机智能生产线中大部件柔性运输和装配需求,提出一种多功能重载AGV的配置形式,基于AGV的特定行驶工况提出一种轮系和智能托架承载力分配方法。基于该方法确定的承载力数值,分别采用渐进结构优化法和Screening优化算法对AGV车体结构进行拓扑优化和多目标尺寸优化研究,获得一种交叉梁设计方案和一组最优结构设计参数。最后对AGV进行静态加载试验,以验证优化结构的可靠性和工程应用价值。
1 多功能重载AGV承载力分配法
1.1 多功能重载AGV的配置形式
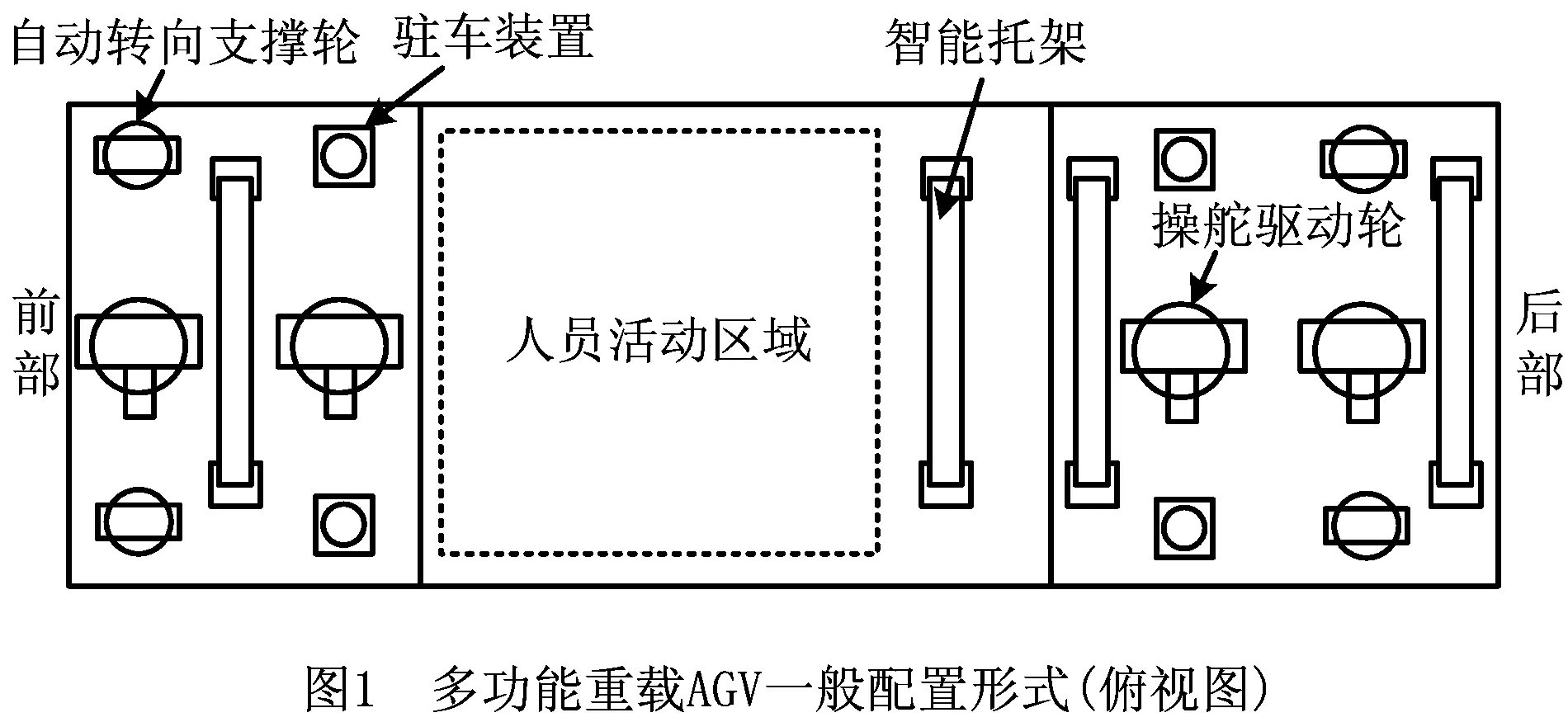
考虑到操作人员需要在飞机大部件底部、内部等区域进行安装调试工作,在车体表面配置4组智能托架装置,多个托架可以稳定承载弱刚度飞机结构件。因为实际运输部件的重量和尺寸较大,要求AGV承载力足够而车身尽可能低,所以提出一种四轮驱动—四轮承载的全向移动轮系布局方式。四轮驱动力依靠尺寸紧凑的操舵驱动轮(简称驱动轮)实现,可以克服两轮驱动力的不足并实现高精度同步转向;AGV的承载力由分布在4个角落的自动转向支撑轮(简称支撑轮)提供,每个支撑轮可以提供足够的承载力并能主动转向。另外,为使车体运动到指定装配站位后固定不动,在车体前部和后部配置4组驻车装置。图1所示为所提多功能重载AGV的一般配置形式。
1.2 智能托架承载力的分配
智能托架的承载力大小对大型部件的运输稳定性影响很大,对其进行合理分配与实时监控不仅可以指导车体结构优化设计,还能有效保障操作人员与部件的安全。本文基于AGV的直线移动状态,提出一种智能托架承载力分配方法。
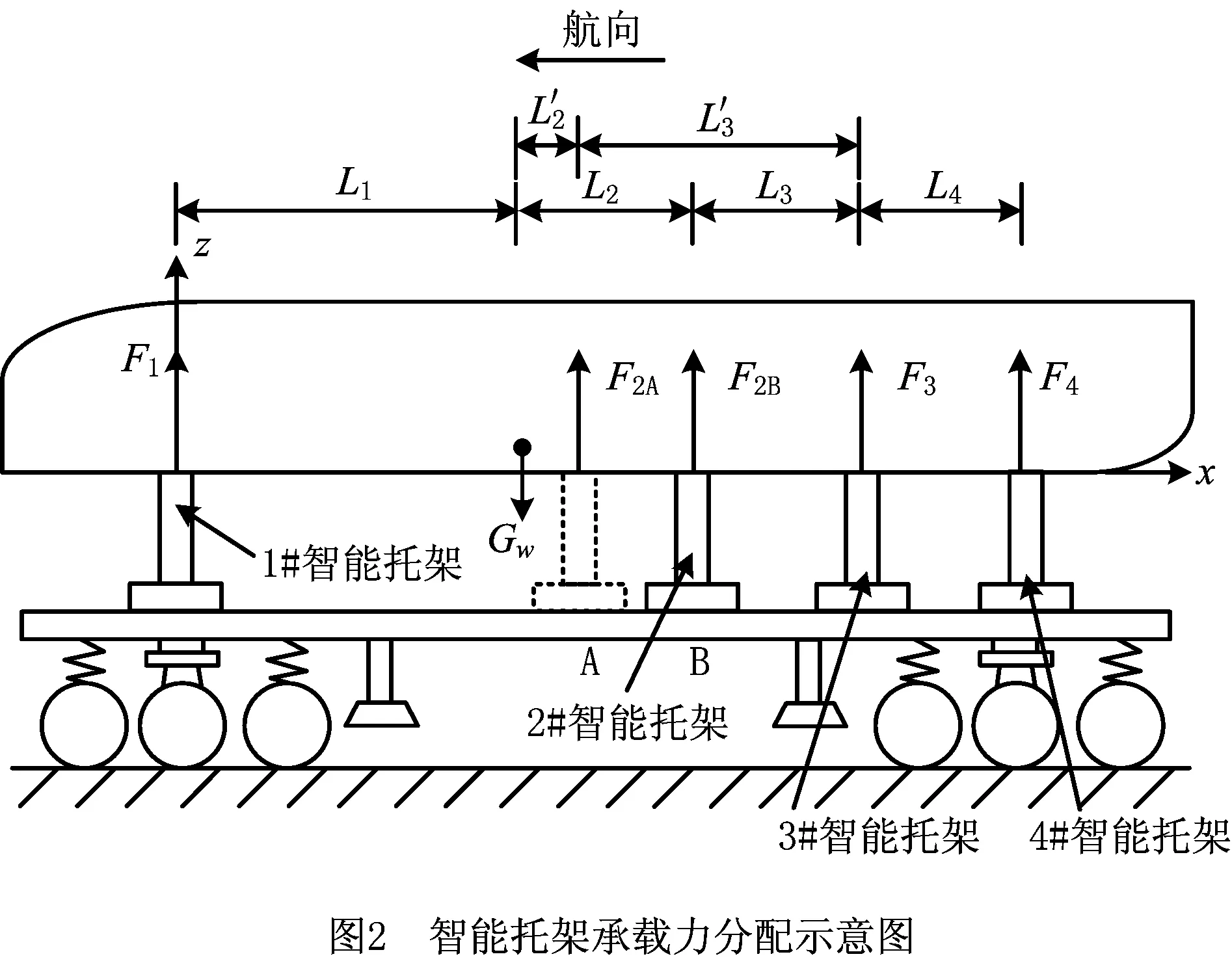
建立如图2所示的空间直角坐标系,原点设定在1#智能托架的托板中心,并设定车身对称轴为x轴,支撑轮与驱动轮连线方向为y轴(垂直纸面向内),垂直地面向上方向为z轴。F1,F3,F4分别是1#,3#,4#托架的承载力,F2A和F2B分别是2#智能托架在A,B位置时的承载力,托架之间以及托架与大部件重心Gw的距离尺寸标注在图中。为保证大部件处于静力平衡状态,各个托架的承载力应满足下列平衡方程:
(1)
假设智能托架的最大承载力为100 kN(根据实际需要可以更改),考虑到2#智能托架在位置切换时不受力,其最小承载力可以设为0。为保证其余智能托架正常工作,本文设定其最小承载力为20 kN。由于AGV前部只有1#智能托架一个承载位,为保证其足够的稳定性,根据大量测试的工程经验设定F1=80 kN。综上所述,各个智能托架承载力应满足如下约束条件:
(2)
确定2#智能托架的承载力取值范围,然后据此计算3#和4#智能托架的承载力。为简化计算,设L=L1+L2+L3+L4,根据式(1)和式(2)分别求解F3,F4关于F2A和F2B的关系式:
(3)
(4)
将式(3)和式(4)分别代入式(2),化简分别得到F2A和F2B的取值范围:
(5)
(6)
式中W=(Gw-F1)L-GwL1。当确定大部件重量、重心位置和各个智能托架的距离后,即可根据式(3)~式(6)合理分配2#,3#,4#智能托架的承载力。
1.3 轮系承载力的分配
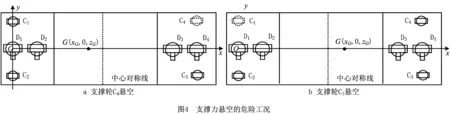
在飞机脉动装配过程中,AGV需要承载着大部件在移动和驻车两种状态之间切换。由于路面凹凸不平,车体移动时可能出现单个支撑轮悬空的危险工况,从而影响整车承载稳定性,有必要对移动状态下AGV轮系承载力的分配进行理论分析。
以驱动轮D1为原点建立如图3和图4所示的空间直角坐标系,并设定x,y,z轴方向与1.2节的坐标系相同。支撑轮和驱动轮坐标记作(xCi,yCi,0),i=1,2,3,4和(xDj,yDj,0),j=1,2,3,4,并有yC1=yC4=-yC2=-yC3,xC1=xC2=xD1,xC3=xC4=xD4。为绘制清楚各轮状态,图3中支撑轮和驱动轮的位置与实际不同,但不影响理论分析。本文将自动转向支撑轮的承载力记作SCi,i=1,2,3,4。各个驱动轮的减振弹簧组因形变而对车体产生一定反作用力,为简化计算,本文假设其为定值并记作SDj=15 kN,j=1,2,3,4。已知飞机大部件关于xz平面对称,车体重心在x轴上,因此可以将飞机大部件重力记为Gw(xw,0,zw),车体自重记为Gp(xp,0,0)。为计算方便,将Gw和Gp等效为整体重量G=Gw+Gp。易知等效重心位于xz平面内,其3个坐标值的求解公式为:
(7)

根据空间力系的静力平衡条件,AGV车体受力情况下的平衡方程为:
(8)
当等效重心位置G位于AGV前部或后部时,其在移动状态下可能分别出现如图4所示的支撑轮C4或C1悬空两种危险工况。整理式(2)可得a,b两种情况下的AGV轮系承载力(为简化表达,驱动轮承载力记作SD):
(9)
(10)
将式(7)分别代入式(9)和式(10),得到用于工程计算的轮系承载力分配方法:
(11)
(12)
2 基于承载力分配法的多功能重载AGV设计
2.1 托架承载力计算
以AGV承载某型机身大部件为例对智能托架承载力进行计算,承载距离尺寸如表1所示,将表中尺寸分别代入式(5)和式(6)即可求出两种工况下2#智能托架承载力的取值范围(单位:kN):
(13)

表1 智能托架承载距离尺寸 mm
根据式(13)计算结果,后续可以对智能托架自动升降系统进行进一步优化,同时利用式(13)指导选用高精度力传感器,以满足量程和测量精度的要求。
2.2 轮系承载力的计算
应用1.3节的计算方法对轮系承载力进行分配,相关计算参数如表2所示。

表2 轮系承载力计算实例的相关参数

续表2
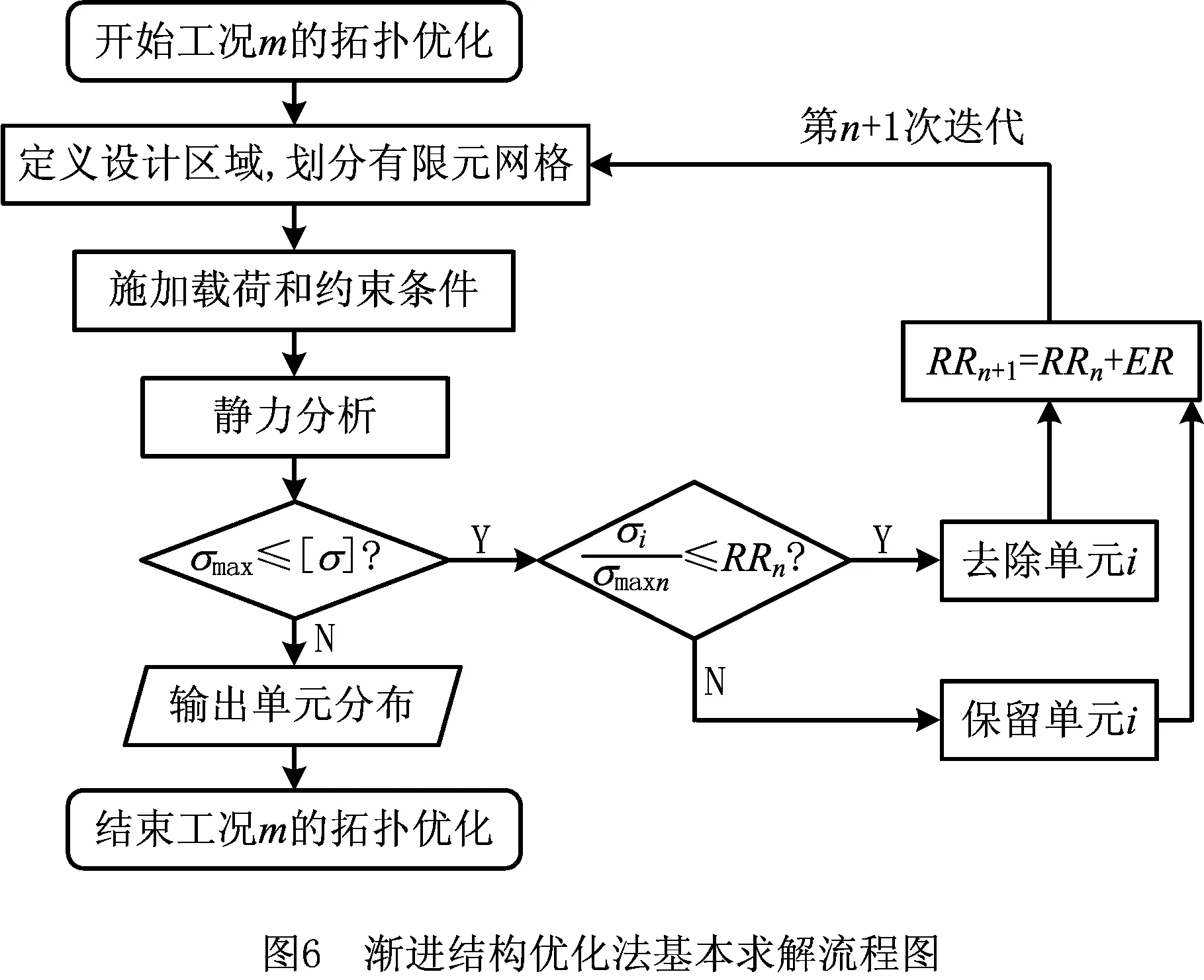
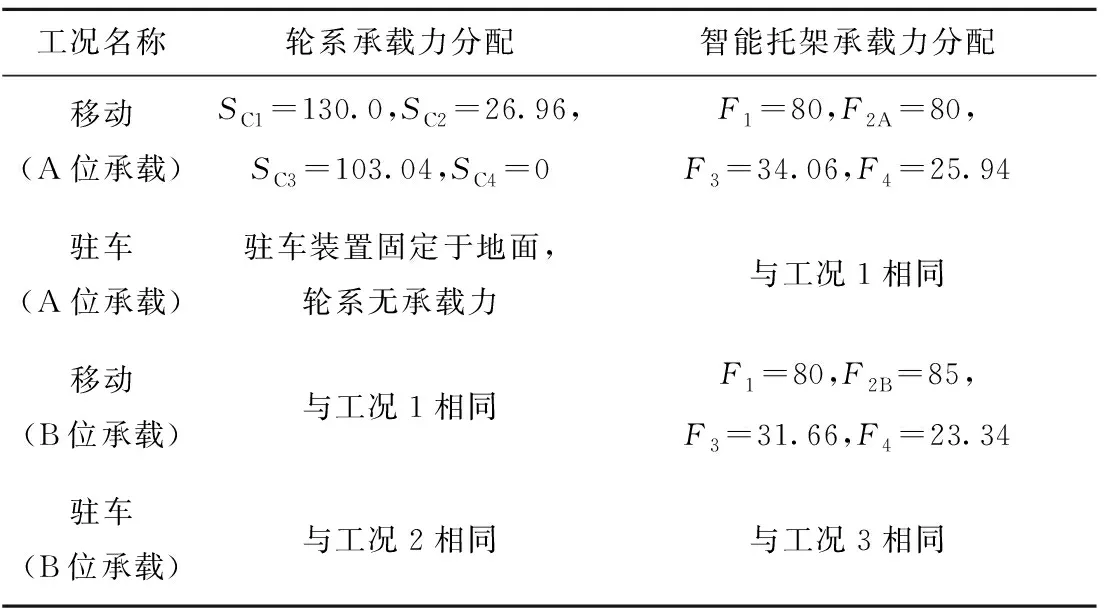
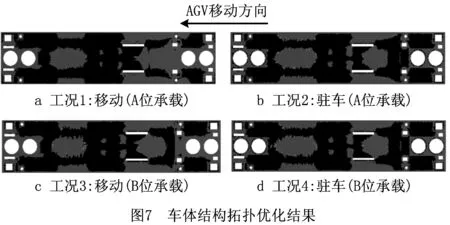
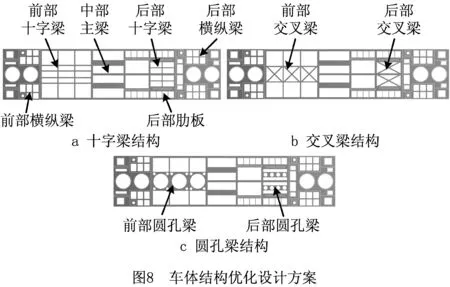
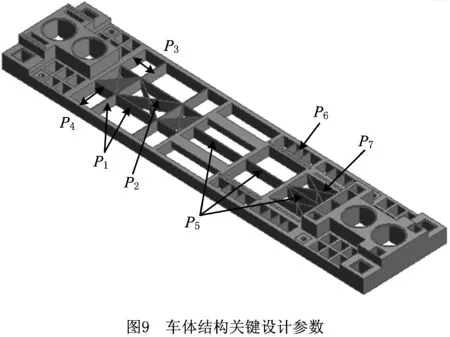
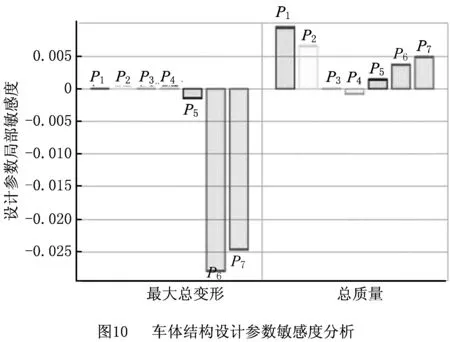
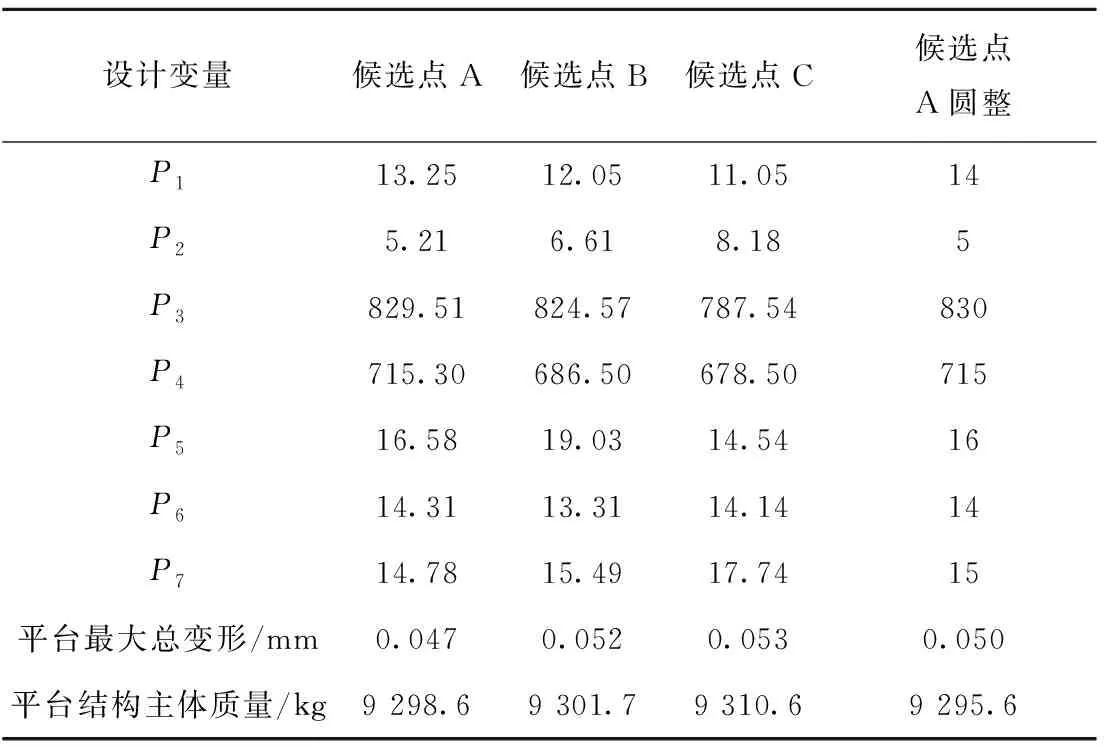
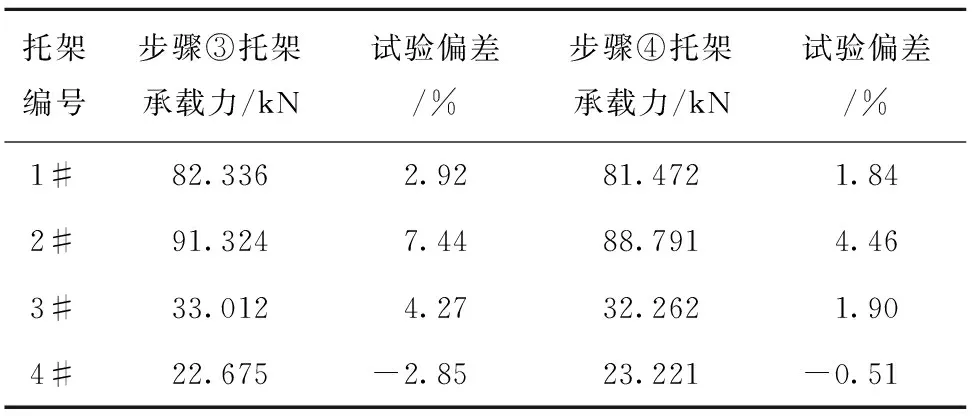
采用式(7)计算等效重心的位置xG=3 999.38 mm,易知xG 由于AGV车身尺寸和负载较大,为了降低能耗并节约制造成本,需要对车体结构进行轻量化设计。对于AGV这样受力非常复杂的机械结构,目前应用广泛的轻量化技术是拓扑优化技术,其中较为成熟的算法主要有变密度法[11]、带惩罚的固体各向同性材料插值法(Solid Isotropic Material with Penalization for intermediate densities, SIMP)[12]和渐进结构优化法[13]等,综合考虑求解速度和精度,本文采用ANSYS软件的渐进结构优化法开展设计,其在特定工况m下的基本求解流程[14]如图6所示,其中:σmaxn为第n个迭代步中车体结构的最大VonMises应力,σi为第n个迭代步中任意单元i的VonMises应力,RRn称为第n个迭代步的删除率,ER为删除率修正参数。Xie等[15]在此基础上加入基于敏感数的删除准则,解决了刚度约束下的拓扑优化问题。ANSYS现有算法在Xie和其他专家成果的基础上进行了完善,可以充分满足优化设计求解。 由承载力分配法可知车体结构在多种工况下的受力情况不同,应综合考虑其对拓扑优化设计的影响。本文将AGV常见的运行工况分为移动(A位承载)、驻车(A位承载)、移动(B位承载)和驻车(B位承载),4种工况下的约束与加载情况如表3所示。设移动工况下的轮系承载力数值与2.1节相同,同时基于2.1节的智能托架承载力取值范围设F2A=80 kN,F2B=85 kN,其余承载力用式(5)和式(6)计算得到。 表3 4种工况下AGV的约束与载荷的设定 kN 首先简化处理车体结构的几何模型,设定结构材料属性为Q345钢,密度为7 850 kg/m3,定义自动转向支撑轮、操舵驱动轮、驻车装置和各个智能托架的安装位置以及平台四周边界为非优化区域,其余部分为待优化区域;然后采用自由网格划分法划分网格,网格尺寸设为60.0 mm,网格数量为185 058,将3.2节设定的约束和负载施加在对应功能模块的安装位置,以结构刚度最大为目标函数,体积去除百分比为70%为约束条件进行拓扑优化,最终得到4种工况下的拓扑优化结果如图7所示,其中黑色部分可以去除,灰色部分予以保留。 通过对上述优化结果进行进一步分析,提出下列结构优化设计方向: (1)AGV前部呈现出较为规则的优化区域,因此考虑保留沿中轴线的材料而去除两侧材料。 (2)前部驻车装置和后部支撑轮周围优化空间较大,这两部分区域虽然对整体刚度影响较小,但是需要操作人员站立作业,因此考虑布置横纵梁结构。 (3)2#智能托架前部区域优化空间较大,该处的刚度对AGV整体变形影响较大,考虑在此处设置中部承载梁和两侧辅助承载梁并去除间隙的材料。 (4)2#智能托架中部区域也显示了较大的优化空间。该处负载较大,可以沿车体中轴线布置主梁并去除两侧区域的材料,同时在智能托架导轨外侧布置肋板以加强导轨安装位置刚度。 根据拓扑优化结果,综合考虑制造工艺性和成本以及机电控制方面的需求,对AGV车体结构提出3种较为可行的设计方案,如图8所示,图中标注了关键的设计结构,主要包括横纵梁、前部梁、中部主梁、后部肋板和后部梁。这些结构的位置及厚度等尺寸对车体整体强度、刚度和模态影响较大,因此需要对其进行进一步优化设计。 以AGV使用频率最高的工况1为例,令除前部梁和后部梁之外的设计结构尺寸保持一致,分别对3种优化设计方案进行静力分析和模态分析,分析结果如表4所示。从表中可见,方案b的强度、刚度和抗振性位于方案a和方案c之间,但其制造难度和成本比圆形梁小,综合考虑后选择方案b作为最终设计方案。 表4 3种优化设计方案的静力与模态分析结果(工况1) 根据工程设计和制造的需要,初步选定的车体结构的关键设计参数如图9所示,其中:P1为前部交叉梁横纵隔框的厚度,P2为前部交叉梁厚度,P3为前部交叉梁横隔框定位尺寸,P4为前部交叉梁纵隔框定位尺寸,P5为中部主梁厚度,P6为后部肋板的厚度,P7为后部交叉梁的厚度。参考工程中常用的筋板厚度尺寸,制定各个设计参数的初值和取值范围,如表5所示。以车体结构最大总变形和总质量为输出参数,在ANSYS软件中采用Central Composite Design方法开展实验设计,设计类型为Face-Centered,样本类型为Standard。实验设计的意义在于为尺寸敏感度分析提供数据基础,其结果可以用于判断哪些设计参数对输出参数有显著影响,从而进行改善。 表5 车体结构关键设计参数的初值和取值范围 mm 实验设计完成后得到的尺寸敏感度分析结果如图10所示,可见设计参数P1~P5对平台最大总变形的敏感度较低,P6和P7的敏感度较高且为负值,说明增大后部肋板和交叉梁的厚度可以显著减小平台变形;另一方面,P1和P2对平台总质量的敏感度较高,其他设计参数相应的敏感度较低。为了增大车体结构刚度并减小质量,应该主要减小车体前部区域的筋板厚度,并适当增加后部区域筋板厚度,以达到综合的尺寸优化效果。 采用ANSYS中的Screening优化算法开展以最小化车体结构总变形和总质量为目标的尺寸优化设计,并设定初始样本点为100。优化后系统给出如表6所示的3组候选优化设计点,可见候选点A的综合性能最好,因此参考其结果并根据工程上常见的筋板尺寸进行圆整,圆整后经过静力分析可知车体结构最大变形为0.05 mm,总质量为9 295.6 kg,优化后的车体总质量小于10 t。 表6 优化设计点的对比和选取 为测试AGV在真实负载下的承载能力,开展了如图11所示的智能托架静态承载试验,试验负载为总重220 kN的模拟部件和配重块,主要试验步骤如下:①手动遥控AGV进入模拟部件下方,将2#智能托架调整为如图11b所示的B位承载状态;②单动顶升1#~4#智能托架,观察承载力的反馈数值,按照第2章承载力分配法进行微调;③模拟飞机大部件运输时的高度,同步顶升各个智能托架200 mm~300 mm,记录此时各个承载力的数值;④模拟AGV到达装配站位后的固定状态,将驻车装置同步伸出100 mm左右以顶起AGV,待示数稳定后再次记录各个承载力的数值。 托架承载力试验结果及其与理论值的偏差如表7所示,可见步骤④的试验偏差比步骤③小,这是因为AGV驻车装置的结构刚性更好,所以其承载稳定性比轮系更好。总之,各个智能托架承载力的最大偏差为7.4%,小于10%,考虑到模拟部件变形和力传感器的误差,试验结果基本达到最优分配平台承载力的目的。另外,试验过程中车体结构未发生明显变形,说明经过拓扑和尺寸优化后,车体结构的强度和刚度可以充分满足工程实际要求。 表7 托架承载力试验结果及其与理论值的偏差 本文针对一种多功能重载AGV开展基于承载力分配法的结构优化研究,得到以下研究成果: (1)提出一种多功能重载AGV的一般配置形式,基于AGV的移动行驶工况和静力平衡方程,对其智能托架和轮系承载力的分配进行理论分析,提出多功能重载AGV承载力分配方法,并给出一种用于飞机装配的重载AGV设计实例。 (2)基于承载力分配法和渐进结构优化法对AGV车体结构开展多工况拓扑优化设计研究,得到一种交叉梁结构设计方案,通过多目标尺寸优化方法进一步获得关键结构的一组最优设计参数。 (3)通过静态承载试验,验证了承载力分配法的可行性,也证明优化设计后的车体结构可以满足工程实际应用要求。 研究开发多功能航空重载AGV,可以满足飞机智能生产线中柔性运输大型部件的需求,大大提高飞机装配效率,也为我国航空制造业智能工厂的建设奠定了基础。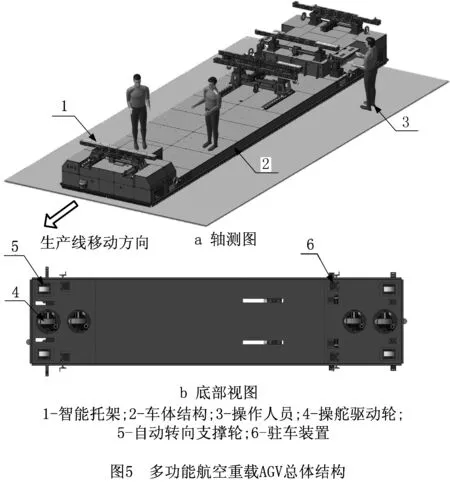
3 车体结构的拓扑优化
3.1 渐进结构优化法
3.2 车体结构的约束与载荷的设定
3.3 拓扑优化的求解与分析
4 车体结构的多目标尺寸优化
4.1 优化设计方案的确定

4.2 多目标优化设计

5 AGV静态承载试验

6 结束语

