去除图像椒盐噪声的自适应迭代均值滤波算法
郭慧娟,白文江,岳云霄,林 菲,白雪飞
(1.太原师范学院 计算机系,山西 晋中 030619;2.太原学院 计算机科学与工程系,山西 太原 030032;3.太原师范学院 汾河流域科学发展研究中心,山西 晋中 030619;4.山西大学 计算机与信息技术学院,山西 太原 030006)
0 引言
图像在获取、传输和接收过程中不可避免地受到噪声污染,所以图像去噪对后续的图像处理有着极为重要的意义。椒盐噪声属于脉冲噪声的一种,其形成原理是图像中某些像素点随机变换为极值点,对于灰度图像,极值点像素值为255和0。椒盐噪声分布因与胡椒和盐粉颗粒相似而得名。有很多经典的算法在去除椒盐噪声方面取得了很好的效果。
传统的中值算法(Standard Median Filtering, SMF)[1-2]以固定窗口大小(如3×3)遍历所有像素点,每一个像素点位于窗口中心。然后,在窗口内按像素值的大小将所有像素点排序,取中间值作为每一个像素点的更新值。文中以Lena 图像中3×3窗口为例来说明中值去噪过程,如图1所示。从图1可以看出,由于椒盐噪声分布往往处于极值位置[3-4],因此取中值往往可以有效避开噪声,这就是中值滤波能有效滤除椒盐噪声的原因。但是随着噪声点的增多,特别在高密度噪声污染时,中值点与真实像素点的偏差越来越大,甚至有可能取到噪声点。针对传统中值算法的缺陷,研究者们提出多种改进策略。自适应中值滤波(Adaptive Median Filtering, AMF)[5]在传统中值的基础上进行了两个方面的改进,一方面增加了噪声检测过程,避免了对所有像素点(无论污染还是未污染像素点)都进行更新,提高了算法的效率和去噪准确度。另一方面窗口可根据实际情况自适应地扩大,改进了传统中值算法中窗口固定的限制,增强了算法的灵活性。但是,中值滤波的核心思想是用图像中某一个像素值来代替窗口中心像素点,这种绝对替换本身具有随机性,并没有充分考虑像素点之间的相互关系。
传统均值滤波(Mean Filtering, MF)是以某一固定的窗口遍历所有像素点,不同的是每一个像素点用其窗口内算术平均值来替换。其处理过程如图2所示。其虽然考虑了窗口内所有像素点的相关性,但没有避免噪声点带来的消极影响。

图1 中值滤波Fig.1 Median filtering

图2 均值滤波Fig.2 Mean filtering
针对传统算法的不足,万丰丰等人结合模糊中值滤波思想提出了自适应模糊中值滤波,取得了很好的去噪效果[6]。彭宏等提出的算法侧重于在均值滤波的同时保留图像的边缘细节[7]。郭远华等提出针对椒盐噪声的开关模糊滤波器[8],所谓开关是指先对图像中的噪声点进行检测,如果是噪声点则执行“开”的去噪处理,如果是非噪声点则执行“关”的操作,直接输出其像素值。江巨浪等提出从k个方向搜索非噪声点,每个方向上找到的第一个非噪声点将参与噪声点的恢复[9]。李佐勇等提出一种新的方向加权均值滤波算法[10],但其对高密度噪声去噪仍有改进空间。
本文结合自适应中值滤波和传统均值滤波,提出了自适应迭代均值滤波算法(Adaptive Iterative Mean Filtering, AIMF)。AIMF算法与前面提到的改进算法相比算法复杂度低,因在滤波阶段保持传统均值滤波,并没有进行方向搜索、加权等处理。文中所用符号说明如表1。

表1 本文符号说明Table 1 Symbol description used throughout this paper
1 本文算法
本文算法的思想是:首先检测噪声点,对非噪声点不做任何处理;然后以噪声点为中心,在滑动窗口内进行去噪。窗口大小由算法自适应地选择。具体步骤如下:
步骤1:输入被污染图像。
步骤2:噪声检测。
标注图像极值为噪声(xi,j=255和xi,j=0)。因椒盐噪声自身的特点,噪声检测相对容易(这里忽略极值噪声点可能产生波动,即噪声点在极值附近某一范围内取值)。
步骤3:在以噪声点为中心的3×3窗口中,计数未污染的像素点个数,记为num,如表1。如果num大于或等于a,则转到步骤(7),否则执行步骤(4)。
步骤4:在以噪声点为中心的5×5窗口中,计数未污染的像素点个数,记为num。如果num大于或等于a,则转到步骤(7),否则执行步骤(5)。
步骤5:在以噪声点为中心的7×7窗口中,计数未污染的像素点个数,记为num。如果num大于或等于a,则转到步骤(7),否则执行步骤(6)。
步骤6:原样输出其像素值。
因该噪声点不满足前面的条件,故暂时未做去噪处理,保持其原来的像素点输出,并记录其个数,记为sum。这些噪声点将在下一轮循环中继续得到处理。
步骤7:计算窗口内未污染噪声点的算术平均值,即将所有非噪声点求和之后除以其个数。算术平均值计算过程可参看图2。
步骤8:遍历完所有图像噪声点后,检查第(6)步记录的未处理噪声点个数,如果sum大于0,循环执行(1)-(8),直到sum等于0循环结束,输出去噪后的图像。算法流程如图3所示。

图3 算法流程图Fig.3 Flow chart of the AIMF
针对如何选择参数a,对a取值为1、2、3和4进行了测试。表2是Lena图像在不同噪声比例下取不同的a值滤波后的PSNR值。从实验数据看出,在低密度噪声时取值1、2和3效果相差无几,取值为4时稍差;在高密度噪声时取值2效果最好,取值1次之,取值3稍差,取值4时效果逊于其它3个值。故本算法中参数a取值为2。
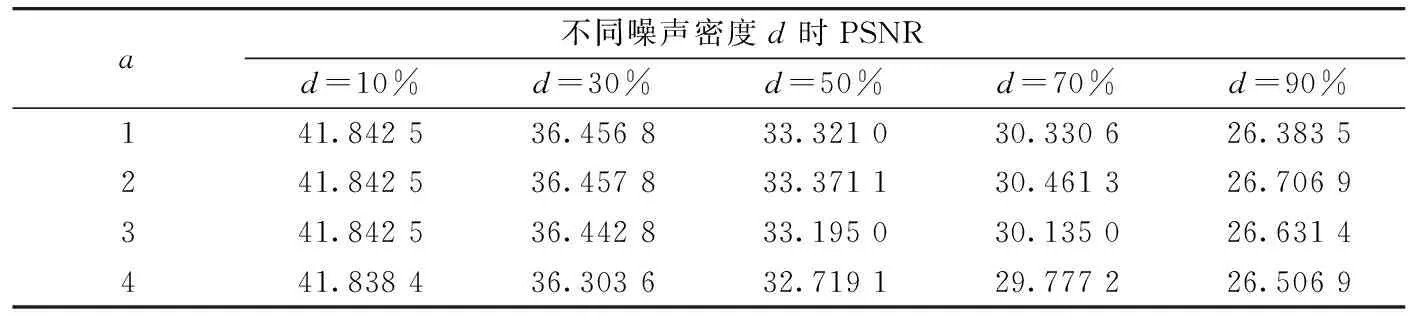
表2 不同a值的Lena图像滤波PSNR值Table 2 PSNR of Lena image at different a value
2 实验结果与分析
实验中测试图像为灰度图像,大小为512×512,分别是Lena、Baboon和Airplane。实验环境为Windows 7(64位)操作系统,处理器Intel Core(TM) i5-3230M,随机存取存储器4 GB(RAM),实验平台Matlab 2012a。为了客观评价算法恢复精度,实验中所有的结果是程序执行100次后的平均值。
本文采用常用的峰值信噪比PSNR(Peak Signal-to-Noise Ratio)作为衡量图像恢复质量的指标。PSNR单位为dB,其计算公式如(1)。
(1)
在式(1)中,MAX代表图像的灰度级,MSE表示原图像与去噪后图像的均方误差。
表3为Lena图像在不同噪声比例下多种算法的恢复结果。从表中可以看出,噪声从10%~90%,本算法都保持着明显的优势。AMF算法较之SMF和MF效果较好。在低密度噪声时,本算法比AMF算法高出约3 dB,但在高密度噪声时,效果更为突出。如噪声比为80%和90%时,本算法比AMF算法高出约13 dB和16 dB。

表3 不同噪声密度下Lena 图像滤波PSNR值Table 3 PSNR of different algorithms to Lena image
从表4可以看出,对于Baboon图像,随着噪声比例的增大,本算法与较好的AMF算法的差距在缩小,从噪声10%时高出10 dB,到噪声50%时高出2 dB,但是随着噪声进一步增大,本算法效果下降缓慢,在噪声为90%时,AIMF的恢复值仍有19.5 dB,而AMF已经下降到10 dB。

表4 Baboon图像去噪后的PSNR值Table 4 PSNR of different algorithms to Baboon image
表5的效果与表3相仿。MF表现较差,SMF次之,AMF在低密度噪声时较之MF、SMF有较大提升,但在高密度噪声时效果下降迅速。本算法无论在低密度、高密度噪声都保持着显著的优势,特别在高密度噪声时,恢复结果远胜于其它三种算法。图4、图5、图6和图7分别是三幅图像在噪声密度为20%、50%、70%和90%的恢复效果,从视觉上展示了本算法的有效性。

表5 Airplane图像去噪后的PSNR值Table 5 PSNR of different algorithms to Airplane image

图4 椒盐噪声密度20%时不同算法的恢复结果Fig.4 Restoration results of different algorithms withnoise density of 20%

图5 椒盐噪声密度50%时不同算法的恢复结果Fig.5 Restoration results of different algorithms withnoise density of 50%

图6 椒盐噪声密度70%时不同算法的恢复结果Fig.6 Restoration results of different algorithms withnoise density of 70%

图7 椒盐噪声密度90%时不同算法的恢复结果Fig.7 Restoration results of different algorithms withnoise density of 90%
3 结论
本文提出了一种自适应迭代均值滤波算法。该算法只对噪声点进行滤波,对非污染点不做任何处理,避免了传统去噪过程中对非污染点进行检测和替换带来的时间消耗和降噪误差。本算法对噪声点进行自适应窗口滤波,对不满足滤波条件的噪声点进行迭代循环处理,提升了算法的去噪能力。本算法与SMF、AMF、MF进行了比较,不仅在低密度噪声(10%~50%)优势明显,而且在高密度噪声(50%~90%)时去噪效果表现突出,如Lena图像在90%噪声时PSNR值达到26.58 dB,表明该算法具有较强的实际应用价值。

