铁矿石运输与车辆调派决策问题研究

翟 耀，谢海涛，吴海波

（安徽马钢汽车运输服务有限公司，安徽 马鞍山 243002）

1 引言

铁矿石运输与调度涉及多种运输方式的衔接，是钢铁企业运营管理的焦点问题之一。如何建立有效的铁矿石集疏运物流体系，一直是学界关注的重点。姚国权[1]主要对曹妃甸港区疏运流程中的流量分配进行了研究，对吞吐量进行了预测，得出集疏运运量需求和运量分配方案，实现集疏运系统的优化。曹巧艳，等[2]对港口汽车疏运业务流程进行优化，以提高港口疏运效率和港口库场利用率。Rob Konings针对集装箱公水联运方式，加快集装箱堆场周转速度，重点解决车船运输与港口装卸有效衔接，以运输装载费用和运输时间最少为目标，均衡及时完成集疏运任务[3]。Wayne K.Talley,Man Wo在研究港口集疏运服务体系过程中，充分考虑港口吞吐量的影响，通过建立经济成本模型和生产函数模型来论证港口吞吐量对于港口集疏运服务体系的重要影响[4]。

本文结合M钢实际，研究M公司自产ZZ精矿物流环节中存在的问题，运用分配与网络模型，从管理决策的角度出发，针对月度运输费用最小建立月度物料调运线性规划模型，针对每天车辆运行时间成本最少建立每天车辆调派线性规划模型，并通过实际应用，验证模型的可行性。

2 问题分析

ZZ精矿是M公司ZZ矿山的主要产品,水汽联运是其主要运输方式，每年约100万t精矿运回本部。M公司ZZ精矿当前的物流流程如图1所示。

ZZ精矿物流流程主要分为四个阶段。第一阶段为汽车运输，铁矿石由M钢自产精矿经汽车运输至周集港；第二阶段为水运，由周集港出发，沿途通过淮河河道进入京杭大运河和长江水道，经水运运抵至B港口集团；第三阶段为水运转汽运，由港口集团1、2、6号码头经汽运至港务原料厂ZZ精矿料堆、仓配码头ZZ精矿大堆和三铁总厂（球团分厂）；第四阶段为港务原料厂ZZ精矿料堆、仓配码头ZZ精矿大堆至各铁厂的铁矿石运输，主要通过汽车、火车和皮带进行运输。

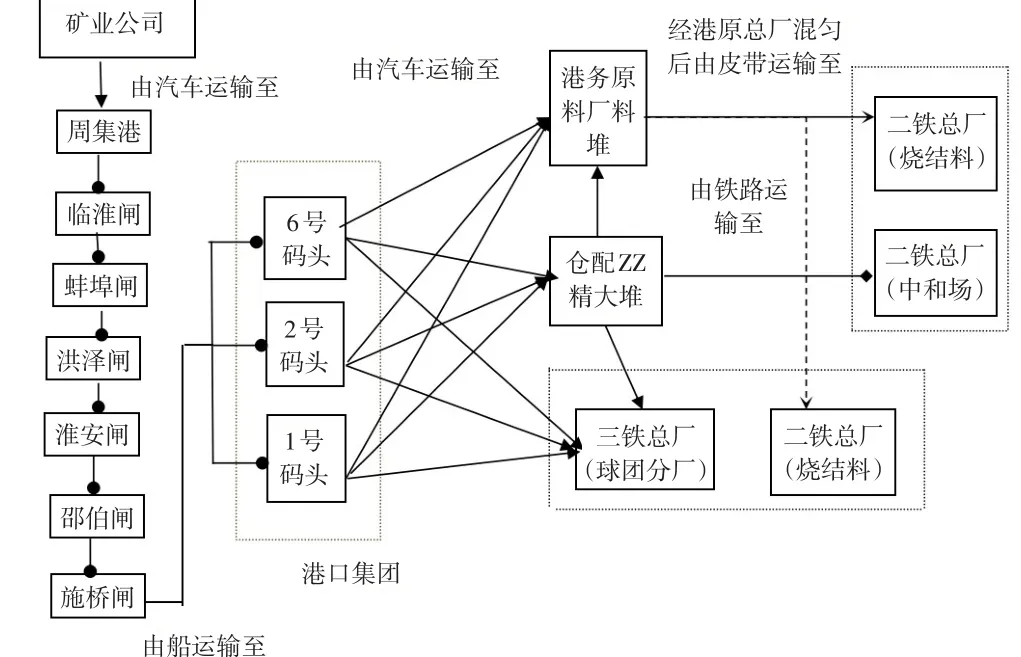
图1 ZZ精矿公水联运物流一体化系统流程图

本文主要研究第三阶段月度供需平衡时的货物运输量的决策及需求方需求量确定时每天运行时间最小化的车辆调派问题，具体包括以下两个方面：

（1）转运问题优化。建立月度转运线性规划模型，合理安排月内每天的运量调配，使月度各条运输线路的总运量达到或接近最佳运量，以使年度重复倒运费用最少。

（2）车辆调度优化。充分权衡各单位使用量、需求量和库存量，对运输企业每天车辆调配科学性进行研究，建立车辆调配线性规划模型，用来指导每日车辆运输作业，使时间成本最小化。

3 ZZ精矿转运问题优化

在ZZ精矿起点节点供应量一定、终点节点需求量已知，起点节点、终点节点以及转运节点各条运输线路运价确定的情况下，确定月度各条运输线路下的月度最佳调运量，以使月度物料调运费用最小。

3.1 转运问题描述

ZZ精矿由水路到达马鞍山港，其年度水运费用由物流公司同船运公司商定且年度固定不变，故水路运费不纳入转运问题描述范围内。对月度ZZ精矿转运问题构建网络图，如图2所示。

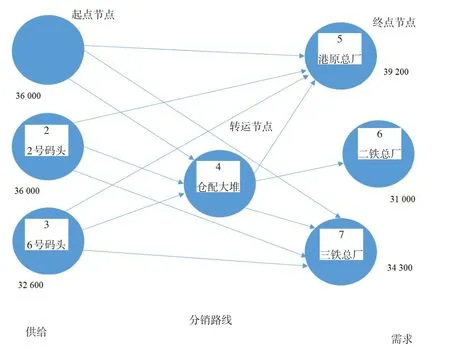
图2 ZZ精矿转运问题节点图

在解决ZZ精矿月度转运费用最小化问题时，可以将该转运问题调整为供求平衡下的月度转运费用最小化问题。各起点节点、转运点至转运节点、终点节点的运费、运输量见表1。

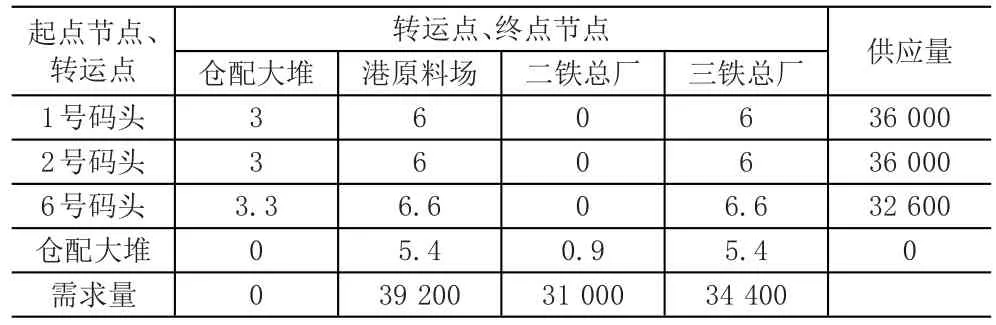
表1 ZZ精矿转运成本、供应需求量表

3.2 转运问题模型的建立

为每个节点和每条弧上的变量确定一个约束。令X14表示从节点1号码头到大堆的运输量，X15表示从节点1号码头到港原节点的运输量，X17表示从节点1号码头到三铁节点的运输量，起点节点的供给约束表达式可以写成：

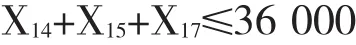
类似地，2号码头、6号码头的供给约束表达式可以写成：

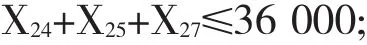
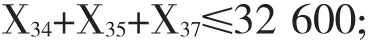
同理，确定转运节点和终点的约束表达式。

最终，目标函数反映了12条运输线路的总运输成本。把目标函数和约束条件组合起来，就形成了一个具有12个变量、7个约束条件的线性规划模型，具体模型如下：

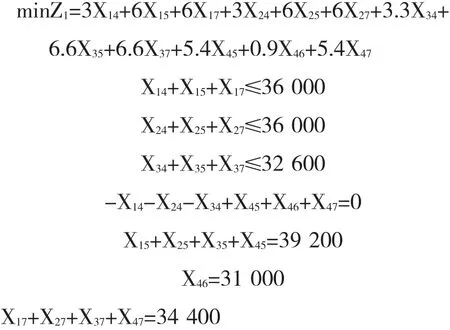
3.3 模型求解

经lingo建模求解后，具体各线路运量见表2，月度转运成本最小为572 760元，该结果可用来指导物流管理人员进行月度各码头卸船及转运任务调派,优先安排1号、2号码头ZZ精矿到港原和三铁，杜绝和减少1号码头、2号码头到仓配大堆的倒运量，避免重复无效倒运问题的发生。

表2 月度ZZ精矿转运问题最优解

4 ZZ精矿车辆调度问题优化

4.1 车辆调度问题描述

目前运输分公司有重型散装物料车20台，结合ZZ精矿运输实际情况建立调度模型。本车辆调度模型中共有8条运输路线，各条运输路线的每趟物料平均运输时间、单趟装载量、单车吨位运输时间成本见表3。

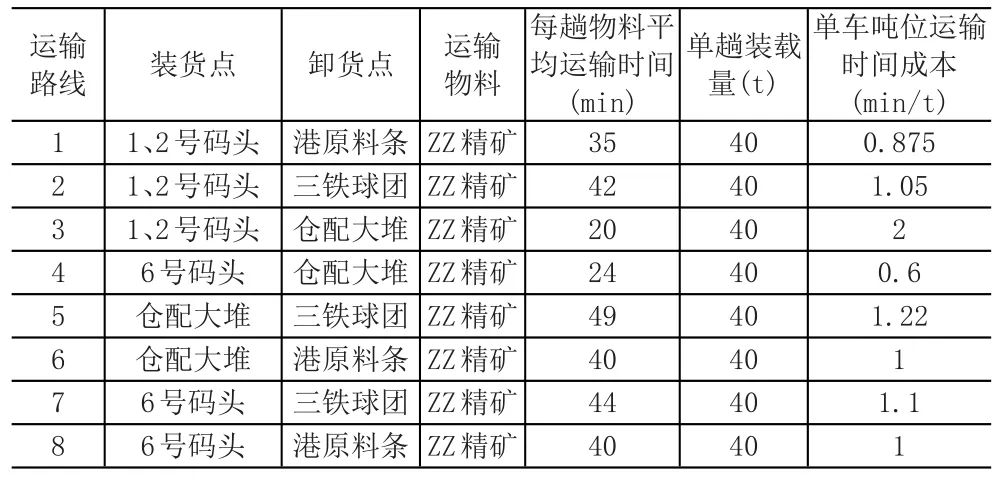
表3 ZZ精矿水转汽运输路线平均时间、吨位表

4.2 车辆调度模型的建立

确定各运输路线的ZZ精矿运输量，建立车辆调派模型，给不同任务分派不同数量的车辆，使得完成所有运输任务的总运输时间最少（总货物运输时间成本最小）。

定义变量如下：

Xi—各项运输任务所需车辆数目/辆，i=1,2,…,8；

Yi—各项运输任务花费时间/h，i=1,2,…,8；

Fi—各项运输任务单趟运输时间/min，i=1,2,…,8；

Gi—各项运输任务运输量/t，i=1,2,…,8；

Hi—单车单趟运输量/t，i=1,2,…,8；

Fi/60—单车单趟运输需要的小时数/h，i=1,2,…,8；

Ii—各项运输任务水转汽清仓时间常数/h，i=1,2,…,8；

Ji—各项运输任务时间补偿常数/h，i=1,2,…,8。

定义各项运输任务单车每吨货物运输时间成本系数：

那么，完成每项运输任务的时间可以表示为：

建立如下关于总运输时间Y最少的线性规划模型:

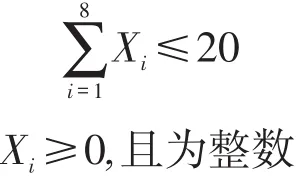
4.3 模型求解

当下达每日具体的运输任务后，即可根据式（1）、式（2）得到对应任务的单车吨位运输时间系数和任务耗时，结合线性规划模型即可确定每日的派车模型，使用lingo软件即可求出每日各项具体任务的派车数，使完成每日各项任务的总耗时最少。

在实际运行时每日的运输任务大多在4-6项之间，现选取某一天的具体运输任务调入模型进行实例验证。

（1）2#码头皖新航668船1 480tZZ精矿进港原；

（2）无任务；

（3）1#码头苏宿货3 165船1 500tZZ精矿进仓配大堆；

（4）6号码头新昇10船2 241tZZ精矿进仓配大堆；

（5）仓配大堆1 621tZZ精矿进三铁；

（6）仓配大堆2 000tZZ精矿进港原；

（7）6号码头中汇108船1 696tZZ精矿进三铁

（8）无任务。

现根据这6项运输任务对20辆运输车辆进行指派，使得总运输时间最短。

物流公司管理人员根据ZZ精矿各使用单位具体场地、生产计划等详情，结合之前的转运问题模型进行模拟，结合港口具体船舶到港计划，综合指派ZZ精矿各生产单位用量（卸货点）运输量，即可明确各运输路线的运输量如下：

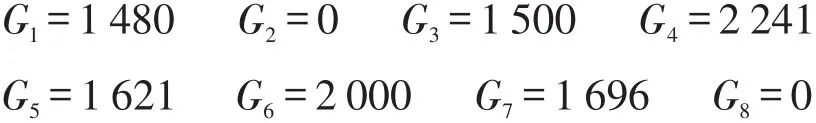
结合各线路运输量对车辆调度模型变量赋值，见表4。

车辆调派线性规划模型如下：

minZ2=(1 480*0.014 6)/X1+(0*0.017 5)/X2+(1 500*0.008 3)/X3+(2 241*0.01)/X4+(1 621*0.020 4)/X5+(2 000*0.016 7)/X6+(1 696*0.018 3)/X7+(0*0.016 7)/X8

表4 车辆调度模型变量赋值表

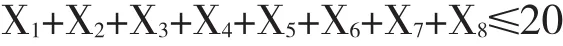
利用LINGO求解出结果：

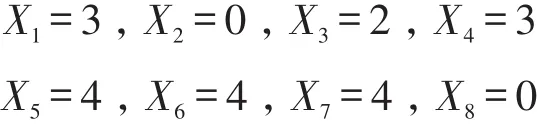
由此得出当日的最终车辆调度方案，见表5。

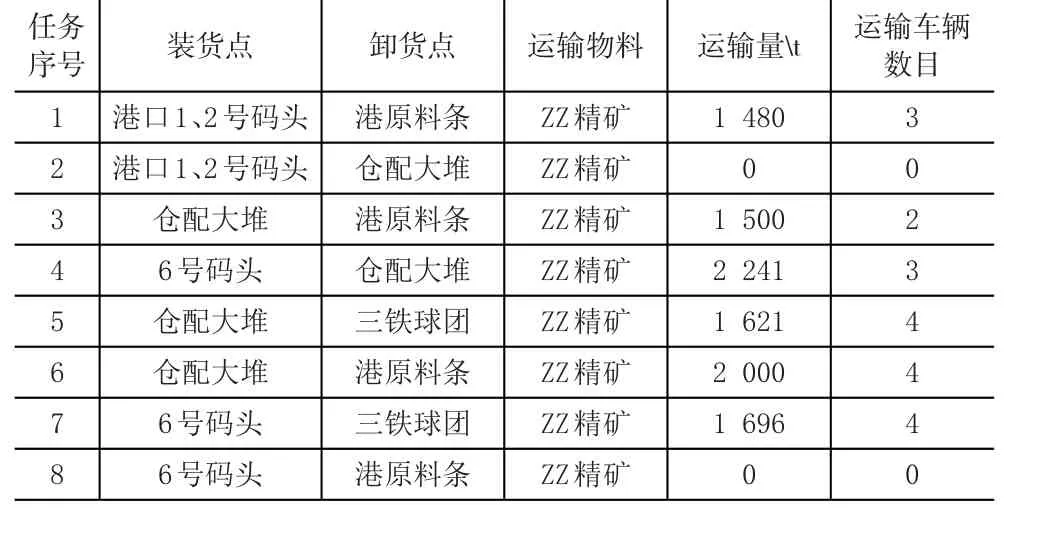
表5 车辆调度方案表

5 结束语

对于物流公司和公路运输企业的实际生产经营来讲，本文所建立的ZZ精矿月度转运模型和每日车辆调度模型具有十分重要的现实意义，它不仅可以通过合理运输降低物流成本，还能够调节料场库存与工厂铁矿石需求量之间的关系，使二者保持在较为平衡的状态，还能有效降低系统整体物流成本。而且由于ZZ精矿到货十分频繁（到货频率一般为1-2d），所以本文建立的模型应用频率也十分高。

在模型运用于生产经营的实际过程中，可以确定月度各运输路线ZZ精矿运输量，用来指导当月每天的排船卸船计划和物料调运，使月度总运输费用最少。其次每天的各物料运输量作为对应的车辆调度模型输入量，通过模型计算得到各运输路线指派车辆数目，用来指导运输单位每天各运输路线相应的派车数目。