考虑交通拥堵的物流配送路径优化
郑乔芳
(南京交通职业技术学院 运输管理学院,江苏 南京 211188)
1 引言
配送作为物流运作中重要的环节,关乎整个物流系统的运作效率以及客户服务满意度,物流配送路径优化也一直是企业和学术界研究的重点。物流配送路径选择不合理导致配送路径重复、迂回,使得配送距离增加,配送道路拥堵使得配送时间延长,配送距离和配送时间的增加使得配送成本增加。以往的很多路径规划问题研究,主要以配送距离作为权重,本文考虑交通拥堵问题,并基于时间成本因素和距离成本因素,提出以有效距离作为权重规划路径,在降低成本的同时,提高客户满意度。
2 问题描述
研究一定区域内单个配送中心、多辆配送车辆对多个配送站点的共同配送路径问题。以配送中心和多个配送站点为节点,配送路径为边,用物流配送过程中投入的车辆行驶里程和时间产生的效用值来量化节点之间配送的有效性,应用柯布-道格拉斯函数模型,物流配送里程和配送时间的投入以指数形式产出效用值,而不是以往研究中的线性形式增长,因为配送距离和配送时间的增加不仅会增加燃油成本、加快车辆磨损和耗费人工成本等,还会引发客户满意度降低、配送效率降低、库存成本增加等问题。用这一效用值来定义有效距离,量化物流配送路径的有效性,物流配送距离和配送时间越大,产生的距离效用值越大,有效距离越大,配送有效性越低,反之亦如此。以有效距离为边的权重,用Floyd算法求解配送中心到其他所有物流节点的有效路径。
3 模型建立
3.1 条件假设与参数说明
相关条件假设如下:
(1)本文假设任意两物流节点之间存在往返路径,且往返距离和时间相同。
(2)本文定义的有效距离并非实际物流配送网络中节点之间的配送距离或地理距离,而是用来度量节点之间配送有效性的量,糅合了配送时间与配送距离的效用。
(3)本文假设的配送距离为路程而非位移,配送时间为平均耗用时间。
参数说明如下:
dij:表示相邻两个节点i和节点j之间的有效距离,也是对应边上的权重,且dij=dji;
eij:表示节点i和节点j之间的有效距离,当节点i和节点j为相邻节点时,dij=eij且eij=eji;
sij:表示车辆从节点i行驶到节点j的路程;
S:表示路程矩阵;
tij:表示车辆从节点i行驶到节点j的平均时间;
T:时间矩阵;
λ:表示距离效用系数;
θ:表示行驶车辆的性能指数;
D:表示有效距离初始矩阵,权值矩阵;
W:表示有效路径矩阵;
Wιj:表示从i到j的最短路要经过Wij点;
α、β:表示路段阻抗函数中的待标定参数;
Qij(t):表示节点i和节点j之间的交通量;
Cij:表示节点i和节点j之间路段的通行能力。
3.2 网络模型
以配送中心、若干个配送站点为节点,以配送中心与配送站点之间的路径为边,构建物流配送网络,在物流配送网络中,将相邻节点i和节点j之间的有效距离dij定义为:
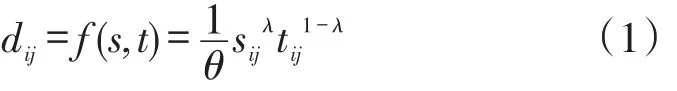
式(1)中λ表示在物流配送网络中其他条件不变的情况下,两节点之间的配送路程增加1%,两节点之间的有效距离对应地增加λ%。1-λ是时间系数,表示在物流配送网络中其他条件不变的情况下,配送时间增加1%,有效距离增加(1-λ)%。λ是可调参数,且0<λ<1;θ为车辆性能指数,且0<θ<1,θ越大表示物流配送车辆性能越好,反之亦然。当物流企业对节约距离成本的关注度高于对节约时间成本的关注度时,可使得λ>0.5,相应地,当物流企业对节约时间成本的关注度高于对节约距离成本的关注度时,可使得λ<0.5。
考虑配送过程中的交通拥堵,通过路段使用的时间会比自由行驶时间长,因而引用路段阻抗函数(BRP)描述出行时间与路段流量和最大通行能力之间的关系,表示为:
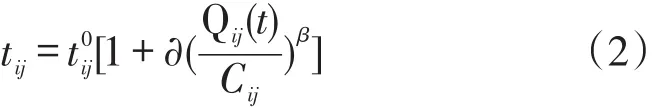
式(2)中,α和β为待标定参数,一般取值:α=0.15,β=4.0,tij表示实际通过该路径所需时间表示通过该路径自由行驶时间,Qij(t)为该路径交通量,Cij表示该路径的通行能力,二者之间有如下关系:

根据观测的相邻节点距离数据和计算的通行时间数据,分别构建S矩阵和T矩阵。

其中,Sij=Sji,tij=tji,给定合适的参数,根据式(1)和式(2),计算并构建相邻节点间的有效距离矩阵D。

式中,dij=dji,配送时间和配送距离的减少都会以指数形式产生效用,以有效距离进行度量,而路径优化的目标是配送中心到任一配送站点之间的有效距离最短。
3.3 模型求解
以有效距离为权重,应用Floyd算法对构建的由一个配送中心和若干个配送站点构成的规则网络进行最优路径的求解,并计算配送中心至各节点的有效距离,详细步骤如下:
(3)按照第(1)和第(2)所描述的方法进行依次插入顶点,一直到所有的顶点插入并计算完得到其中是从i到j的只允许以1、2、...、v作为中间点的最短路径中最小的有效距离,即从i到j中可插入任何顶点的路径中最小的有效距离,因此E(v)是节点之间最短有效距离矩阵,可由E(v)来查找任意两个节点之间的最短有效距离。
最后,在求得有效距离矩阵的同时,建立有效路径矩阵 W=(wij)n×n,wij表示从i到j的最短路要经过wij点:初始值,在每求得一个有效距离矩阵E(k)时,按照以下方式产生对应的新路径矩阵W(k):


3.4 数值模拟
假设有1个配送中心H需要向该区域内20个配送站点共同配送货物,分别用数字1~20进行编号,配送中心H与各节点之间的配送距离s见表1,假设物流配送运作过程中,对于配送距离和配送时间注重程度是一致的,引入参数 λ=0.5,θ=0.9,α=0.15,β=4.0,选定时间窗、通行能力、交通量并计算出相邻节点间有效距离数据见表2。
根据表2中相邻节点间的有效距离作为权重,构建权值矩阵D,运用matlab,Floyd算法求解得出物流配送网络中各节点间的有效距离,见表3。
同时,在配送时间因素和配送距离因素同等重视的情况下,λ=0.5,通过算法求解得出物流配送网络中任意两节点之间的有效路径,其中配送中心H至各配送站点的有效路径信息见表4,通过数值模拟,以有效距离作为权重求解得出的有效路径更贴近实际需要,通过调节λ值可以调节有效路径的选择,当面对配送及时性要求较高的客户,可以适当降低λ值,反之,可以适当提高λ值。考虑交通拥堵因素,量化为时间效用,作为路径选择参数,避开交通拥堵路段,更能提高配送效率。尤其在规划大型物流配送网络时,节点和边较多,可以从宏观角度规划路径,有效规避拥堵路径,提高配送网络的稳定性,不易因交通拥堵而影响物流配送。

表1 物流配送网络各节点配送距离

表2 路径相关参数表

表3 节点间有效距离数据

表4 有效路径
4 总结
以配送路径选择为基础,考虑了实际运作中的交通拥堵因素,将其量化为时间效用值,构建有效距离函数,与以往对于配送距离、配送时间和成本之间构建线性关系不同,以指数形式量化配送时间和配送距离对路径选择的影响效用,反映配送服务过程中,配送时间或配送距离的增加,都会以指数的增长影响到客户满意度,尤其是当前互联网电商平台发展背景下,配送服务要求越来越高,以有效距离构建权值矩阵,应用Floyd算法求解得出配送网络中各节点之间的优化路径。该路径的选择同时考虑了交通拥堵影响下的时间因素和距离因素,更贴近实际运作,为路径的优化以及配送网络的构建提供借鉴和参考。

