基于群组信息改进矩阵分解的群组推荐方法

尹 青 山

(辽东学院工程技术学院 辽宁 丹东 118000)

0 引 言

随着信息时代的发展，传统的目标明确的信息搜索方法使用户难以从海量数据中得到满意的感兴趣信息，而推荐系统通过用户对项目的行为和偏好，将信息搜索转变为信息主动发现，从而实现针对性的推荐[1]。但传统推荐较多倾向于生成个体用户推荐，而随着网络群组的兴起，用户组建或加入感兴趣的信息群组越来越普遍，群组增强了用户间的交流和信息共享，若向用户群组直接生成推荐建议则进一步减少其感兴趣项目的搜索过程和检索时间[2]。因此群组推荐成为新的挑战，但在推荐过程中群组所扮演的重要角色往往被忽略[3]。

已有群组推荐研究主要分为推荐使用方法的融合和个体推荐结果的融合。刘鲁等[4]由群内个人偏好模型推导生成群组偏好模型，并将群组模型代入个人协同过滤推荐方法生成群推荐；王建芳等[5]提出基于影响因子和偏移因子和非对称因子约束相似矩阵的群组推荐，算法的收敛和预测精度具有明显优势；Kim等[6]的两步混合推荐算法先根据关键词搜索近邻并利用个人协同过滤形成粗推荐表，然后从粗表中删除兴趣不高的信息；Kassak等[7]提出协同过滤和基于内容相融合的群组推荐，在为群内所有用户生成双列表基础上，通过融合策略由内容推荐列表对协同过滤的列表进行重排；Ortega等[8]采用矩阵分解之前用户评分矩阵合成群矩阵、分解后用户分解矩阵等权重、不等权重合成为群矩阵三种矩阵分解策略得到最终群推荐；Chen等[9]提出OWA算子与相关系数结合的群体推荐，在确定专家替代方案偏好值基础上，计算总体偏好值与专家个体偏好值相似度，并由备选方案的相关系数调整专家权重，使组共识达到预设阈值；Pirasteh等[1]采用非对称性来评价用户相互影响及相似矩阵分解，其群推荐在冷启动表现更好；陶永才等[10]根据群组内用户的签到偏好提出群组兴趣点(项目)的推荐算法，其模型的推荐准确率有明显提高；夏立新等[11]在用户偏好聚类基础上，将情境数据融入群组的行为特征发现以提高推荐准确度，由各群组的历史评分根据协同过滤思想形成预测推荐。蔡玲等[12]首先采用协同过滤生成群推荐项目候选集，然后对群偏好聚类后将反映全体偏好的项目子集增加到候选集中，形成增强推荐子集，由增强子集中生成推荐列表。Pessemier等[13]提出基于多个评价指标的推荐算法，实验比较发现，协同过滤算法与偏好矩阵分解相结合对数据稀疏和推荐精度有明显的提高改善。

然而，已有算法方法存在数据稀疏和可扩展性较弱的问题，且未考虑群组特征对推荐结果的影响。为此，本文以融入群组信息的矩阵分解为基础模型，提出基于改进联合矩阵分解的群组信息推荐算法，将用户的群组偏好信息引入联合矩阵分解，并生成个人预测。采用了三种策略进行个人评分融合，更有效地实现群组推荐，并通过对比实验验证了算法的有效性。

1 算法设计

1.1 群组推荐算法框架

根据用户的偏好及用户加入群的信息对群组的偏好进行预测，设系统中的N个用户表示为U={u1,u2,…,uN}，M个项目为V={v1,v2,…,vM}；用户偏好评分用矩阵R={ri,j}N×M表示，其中ri,j表示ui对vj的偏好值；G={g1,g2,…gl,…,gL}为推荐系统中的L个群组；而用户的群组信息矩阵为A={al,i}。GAi,m={gl|al,j}=1∪al,m=1,gl∈G}表示任意两用户ui和um共同拥有的群组，GAi,m≠φ表明两用户存在相关性si,m=Sim(ui,um)，所有用户组成相关性矩阵S={si,m}。群组的偏好评分由矩阵D={dl,j}表示，dl,j由群gl的所有成员对vj的评分组成，即：

dl,j=h(ui,vj)

(1)

式中:h(·)为评分合成所需的策略函数，且ai,j=1。在充分考虑群组相关特征的基础上，本文算法的群组推荐框架如图1所示。

图1 基于改进矩阵分解的群组推荐框架

根据图1框架，算法过程根据用户评分及其入群信息通过矩阵分解生成群组推荐，整个过程主要由如下三部分组成：

(1) 用户相关性计算：相关性计算根据群组和用户入群情况等信息计算，主要包括用户加入的群组及数量、共有群组及数目、共有群组大小等信息。

(2) 矩阵分解：将关联信息融入矩阵分解，计算群内单用户的偏好评分。

(3) 评分合成：将单用户评分通过合适的评分合成策略合成群组的最终评分及群推荐列表。

1.2 群信息计算相关性矩阵

不同用户加入同一群组的情况在一定程度上反映了两个用户之间的相关性，而这种共有群组越多，其兴趣或对某项目的评分则可能越相似[5]。为此，构建如图2所示群组-用户关系图，以更好地描述用户之间有关群组信息的关联性，图中虚线表示两用户拥有着共同的群组，则定义相关性si,m为：

(2)

式中：|GAi,m|表示共同群组的个数。

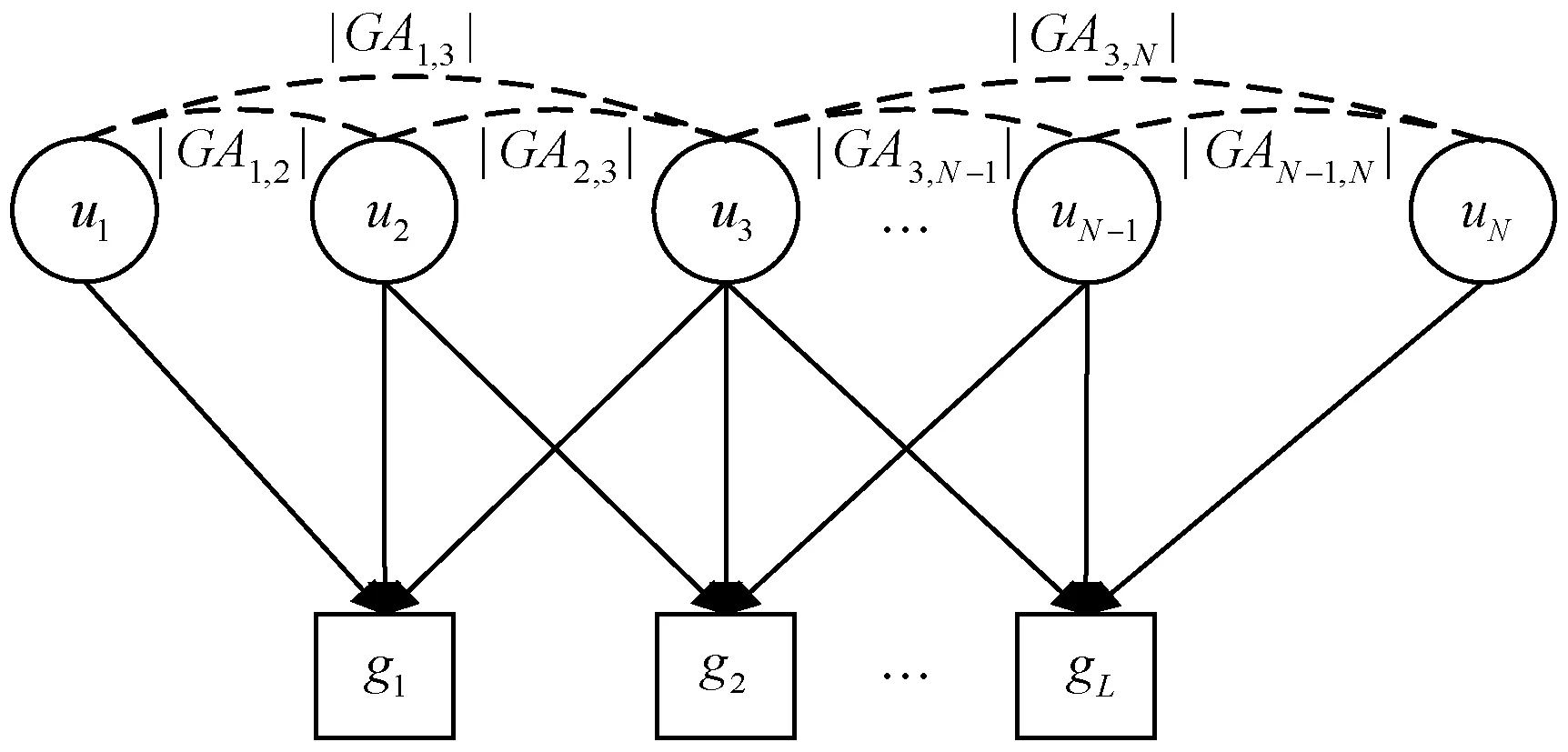
图2 群组-用户间的二维关系图

另外，用户共有群组的规模也影响两用户的相关，通常共有群组的群内人数越小，则其组内成员之间感兴趣的项目越相似[8]，由此si,m的计算可以进一步优化为：

(3)

式中：|gl|为群组规模。

1.3 联合概率矩阵分解

本文将根据群组结构信息计算的用户相关信息集成到矩阵分解中，其具体过程如下：

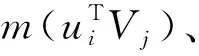
(4)

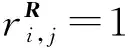
通常用户间的相关性越高，其特征向量间越相近[9]，据此可得高斯先验分布为：

(5)

设项目vj的特征向量服从期望值为0的先验高斯分布，即：

(6)

根据以上定义，由贝叶斯估计可得后验概率分布为：

(7)

为便于求解，对式(1)两边取对数可得：

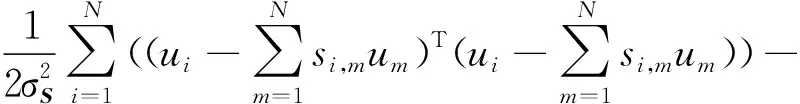
(8)

式中:K为矩阵分解时的潜在特征维度；C为常数矩阵。对式(2)进行等价变换得：

(9)

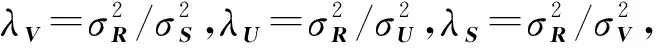
(10)

(11)

式中：m′(x)=exp(-x)/(1+exp(-x))2为m(x)导数。

1.4 评分合成

群推荐最后进行个人预测评分的合成，以获取最终群组对项目的评分根据矩阵分解方法过程，用户ui对项目vj的预测评分为：

(12)

本文选取了均值、最小痛苦和最大幸福三种策略进行融合计算群组的最终推荐预测，获取评分后分别形成推荐列表。均值策略以群组内成员评分的平均值为群组的最终预测，其计算公式为：

(13)

最小痛苦策略将最终的组预测与群组内当前评分满意度差的成员的评分意见一致，其以成员评分的最小值为最终群组评分，计算公式为：

(14)

而最大幸福策略与最小痛苦相反，以群组内成员最大评分值为最终群组对项目的评分，计算公式为：

(15)

根据三种策略，获取最终融合评分，并形成群推荐，整个过程如算法1所示。

算法1改进矩阵分解群组推荐算法

输入：用户集U，项目集V，用户对项目的评分R，群组G，群结构矩阵A，最大迭代次数itmax

输出：群推荐D

FORi=1,2,…,M

FORm=1,2,…,M

IFi≠m

根据式(3)计算用户ui和um的相关性Si,m；

END FOR

END FOR

对用户集和项目集进行随机初始化；

FORit=1,2,…,itmax

FOR each∈R

根据式(10)和式(11)计算的梯度值进行更新：

ui=ui-α∂L/∂ui

vj=vj-α∂L/∂vj

END FOR

END FOR

FORl=1,2,…,L

FORj=1,2,…,N

根据式(13)-式(15)的三种策略分别合成群组推荐列表；

END FOR

END FOR

2 运算复杂度分析

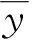
3 实 验

CiteULike是一个用于增强学术交流、可创建同领域或共同爱好的兴趣群组的科研网站，与本研究所需的数据刚好契合，为此从该网站爬取并筛选了13 597个用户，5 108 972篇学术文章，3 916个群组，用户收藏文章信息7 839 301次。选取了推荐准确率(Precision)、召回率(Recall)、平均准确率(MAP)和平均倒排(MRR)四个评价指标。Precision反映兴趣项目占总推荐项目的比例，Recall反映被推荐兴趣项目占总兴趣项目的比例，MAP反映了推荐的准确性和排序，MRR反映出群组越感兴趣的项目被推荐得越靠前，则推荐效果越好。四个指标可客观地衡量推荐的准确性和排序[13]，其计算式为：

(16)

(17)

(18)

(19)

其中：K(gl)表示群组推荐集；T(gl)为测试集中用户偏好的项目全集；Pre(rl,k)表示该项目在K(gl)和T(gl)交集中的排列位置；rank(Fl)表示在K(gl)和T(gl)中首个共有项目在列表中的位置。为验证本文算法(简记为JPD)的推荐性能，选用UserKNN和PMF方法作为算法个人评分阶段的对比算法，以均值(AVG)、最小痛苦(LM)和最大幸福(MP)三策略合为评分合成方法，以WBF、TSBook和MultiRec三种最新群推荐方法进行整体算法性能比较。实验中训练集和测试随机划分，各占总数据集的80%和20%，矩阵分解的最大迭代次数为200，UserKNN算法中邻居用户数设置为30，实验结果为20次实验的平均。

3.1 算法参数对算法性能影响分析

3.1.1推荐个数d影响

图3为实验中算法推荐个数分别设置为d={10,20,30,40}时各算法在不同评价指标下的推荐结果。UK_AVG、UK_LM和UK_MP及PMF_AVG、PMF_LM和PMF_MP分别为采用UserKNN算法和PMF算法进行评分的三种策略，而JPD_AVG、JPD_LM和JPD_MP为本文算法采用的三种评分合成策略。可以看出，在三种评分合成策略下，本文算法在四个评价指标的推荐效果均优于其他方法，说明以用户相关性形式将群组信息引入可以有效提高基于矩阵分解的群推荐的推荐效果。从图3中各算法在不同推荐数下的实验结果还可以看出，d值从10变化到20时，推荐结果对应的各评价指标有较快的变化，而d=20后，各指标值变化相对缓慢，这主要是因为推荐列表在达到一定长度(d=20)后，算法对于推荐列表的靠后部分的推荐项目偏好差距不大。

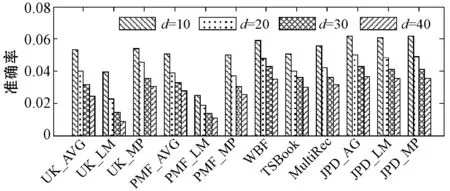
(a) 不同推荐数下的推荐准确率比较

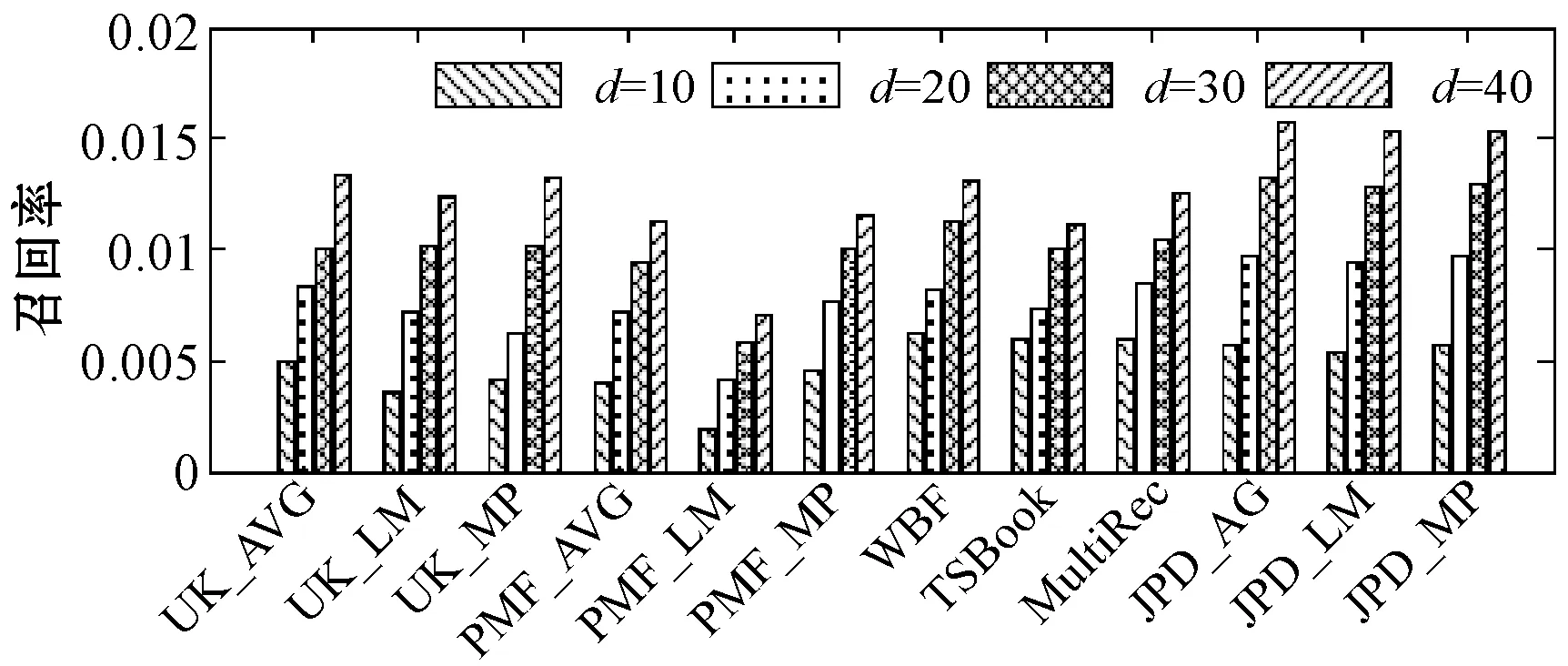
(b) 不同算法的推荐召回率比较图3 各算法在不同d下的准确率和召回率

3.1.2特征向量维数K影响

算法在进行矩阵分解时，特征向量维数K的设定对算法的推荐结果存在一定的影响。K值过小会使分解得到的特征向量无法完整表达潜在的特征，而K值过大又迅速增大算法的复杂度。为此，设置d=10，分析K={5,10,15,20}下算法的推荐性能，实验结果如图4所示。可以看出，不同特征维数下，本文算法具有较好的推荐性能，且在不同K值下，实验结果相对于PMF算法具有更好的稳定性。当K=10时，本文算法具有较好的推荐性能和推荐稳定性，后续实验中设置K=10。

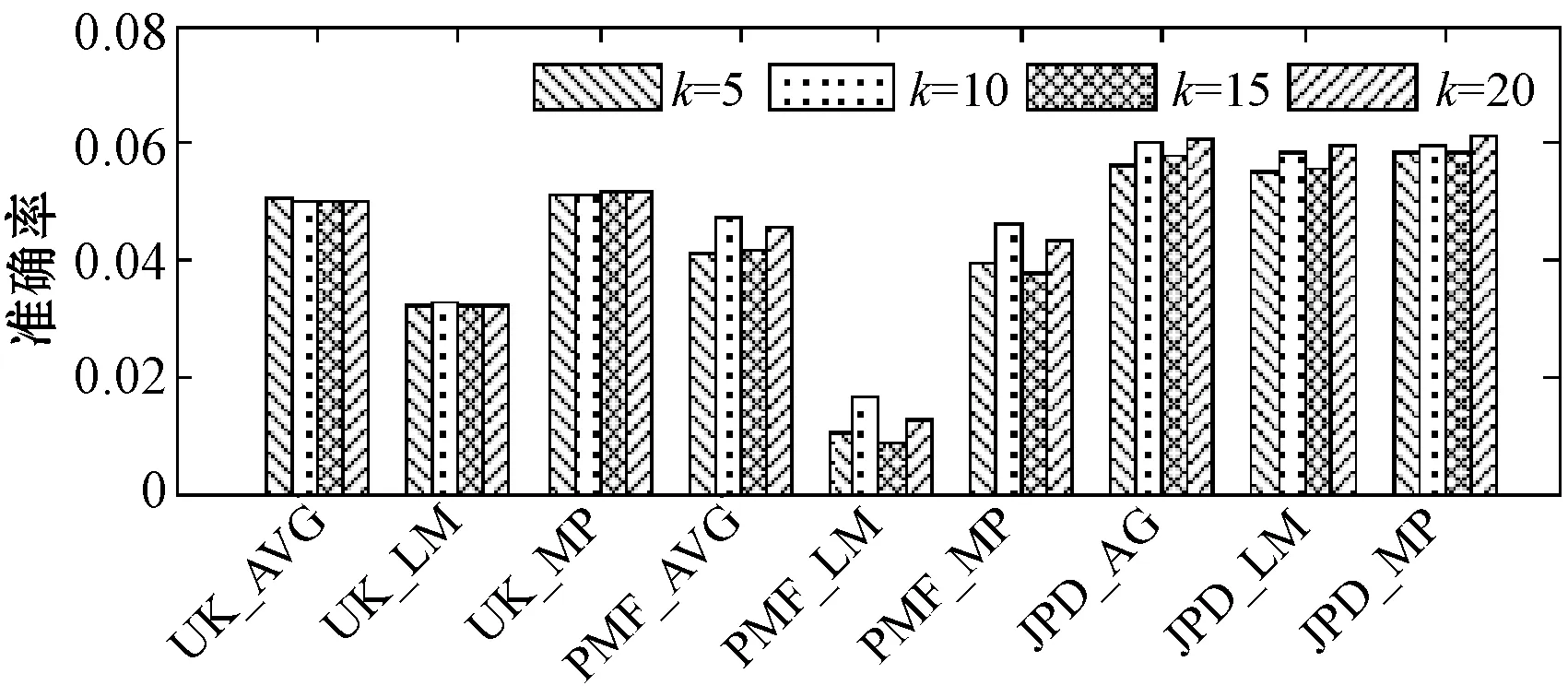
(a) 不同算法的推荐准确率比较

(b) 不同算法的推荐召回率比较图4 各算法在不同K下的推荐准确率与召回率

3.1.3社会化参数λS的影响

λS影响由群组信息计算的用户相关性在引入到后续矩阵分解时的参与指数，本文算法在不同λS={0.001,0.01,0.1,1,10,20,30,40,50}值下的实验结果如图5所示。可以看出，λS对算法的推荐性能影响较为显著，当λS取值在0.001到10时，三种评分合成策略下，算法的推荐性能迅速提高，且在λS=10时达到最大值；当λS值继续增大时，算法的推荐性能变化不明显，这证明了基于群组结构信息生成的用户相关性对算法性能提升的有效性，且当λS=10时，可以取得较好的推荐性能。

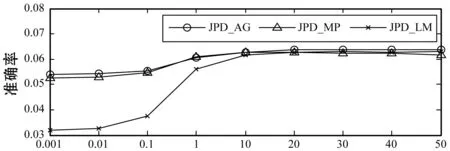
(a) 不同算法的推荐准确率比较

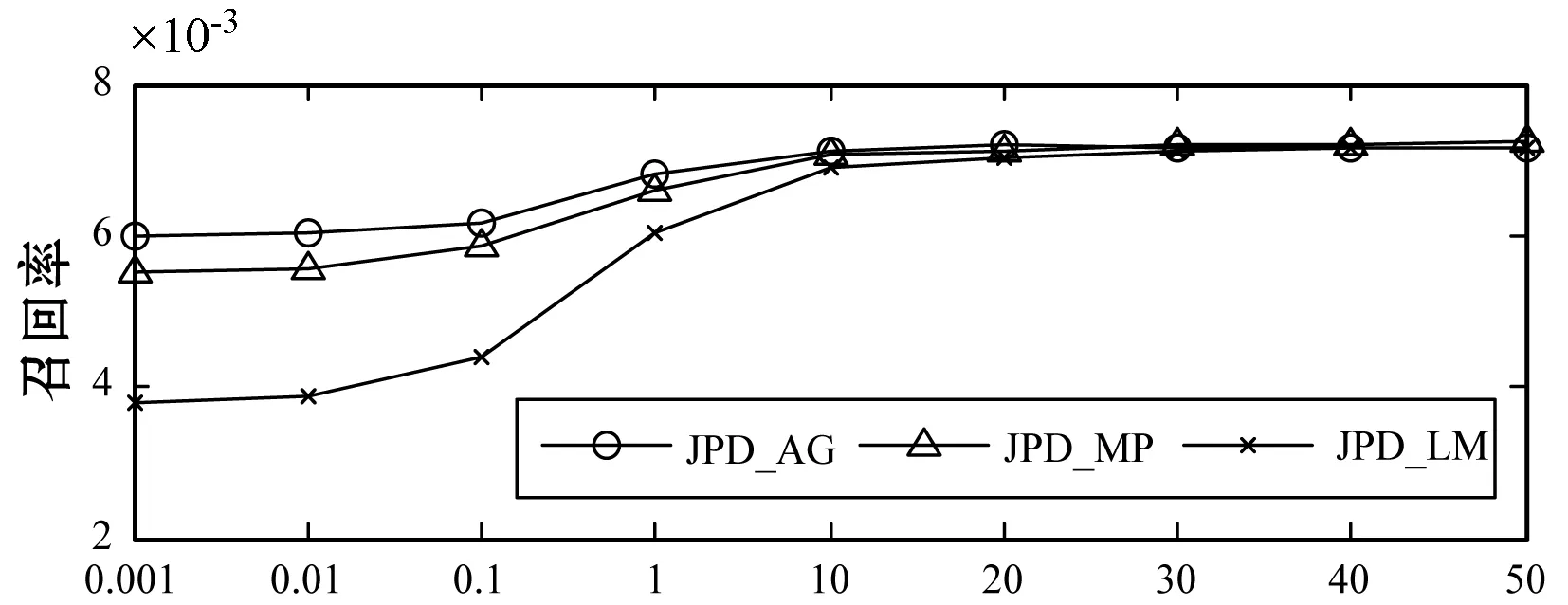
(b) 不同算法的推荐召回率比较图5 各算法在不同λS值下的推荐准确率与召回率

3.2 算法推荐性能分析

表1为算法在所涉及的各参数影响分析后，取λV=λU=0.001、λS=10、K=10、d=20时，各算法的群组推荐性能比较。可以看出：最小痛苦评分合成策略在大部分情况下，其推荐性能最不理想，主要原因是其会造成对多数用户都感兴趣项目的忽视；本文算法的基础部分JPD算法在三种评分合成策略下的推荐性能变化不大，说明本文算法的基础算法具有较好的稳定性；从整体看，WBF、TSBook、MultiRec三种算法及本文算法在各指标上的推荐性能均优于UserKNN和PMF算法。与WBF、TSBook和MultiRec算法相比，本文算法在精确率和召回率上均优于三种比较方法，而在MAP和MRR两指标上，性能表现相差不大，说明本文算法的推荐结果在推荐顺序满意度上与WBF、TSBook和MultiRec三种算法相当，而在推荐精度上明显优于三种比较算法。

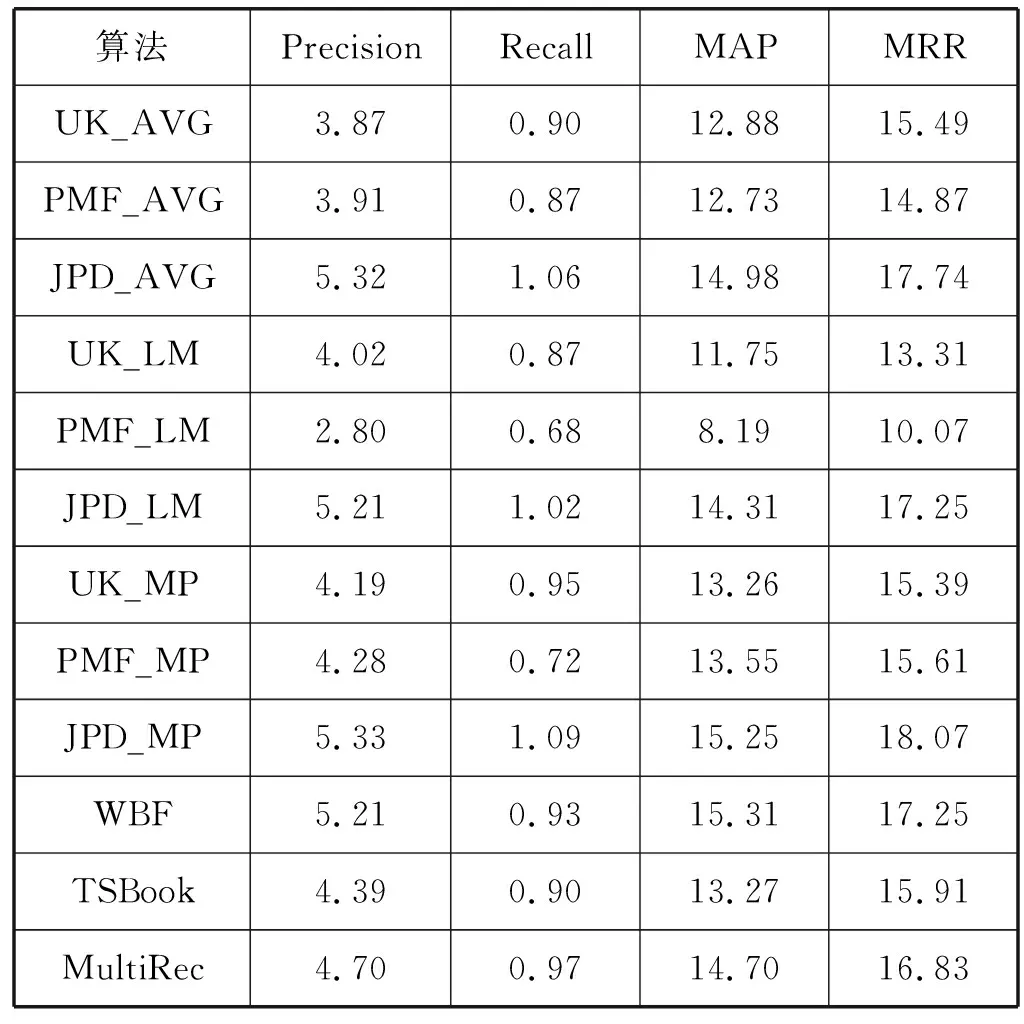
表1 推荐算法性能比较实验结果 %

4 结 语

本文提出一种基于改进矩阵分解的群组推荐算法，与已有的群推荐算法的性能对比实验结果表明，本文算法在准确率等多个评价指标上表现更优。但算法在考虑用户评分和群组结构等信息基础上，还需进一步分析融合广泛存在的其他社会化群组信息，以提高算法的推荐性能。